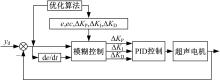
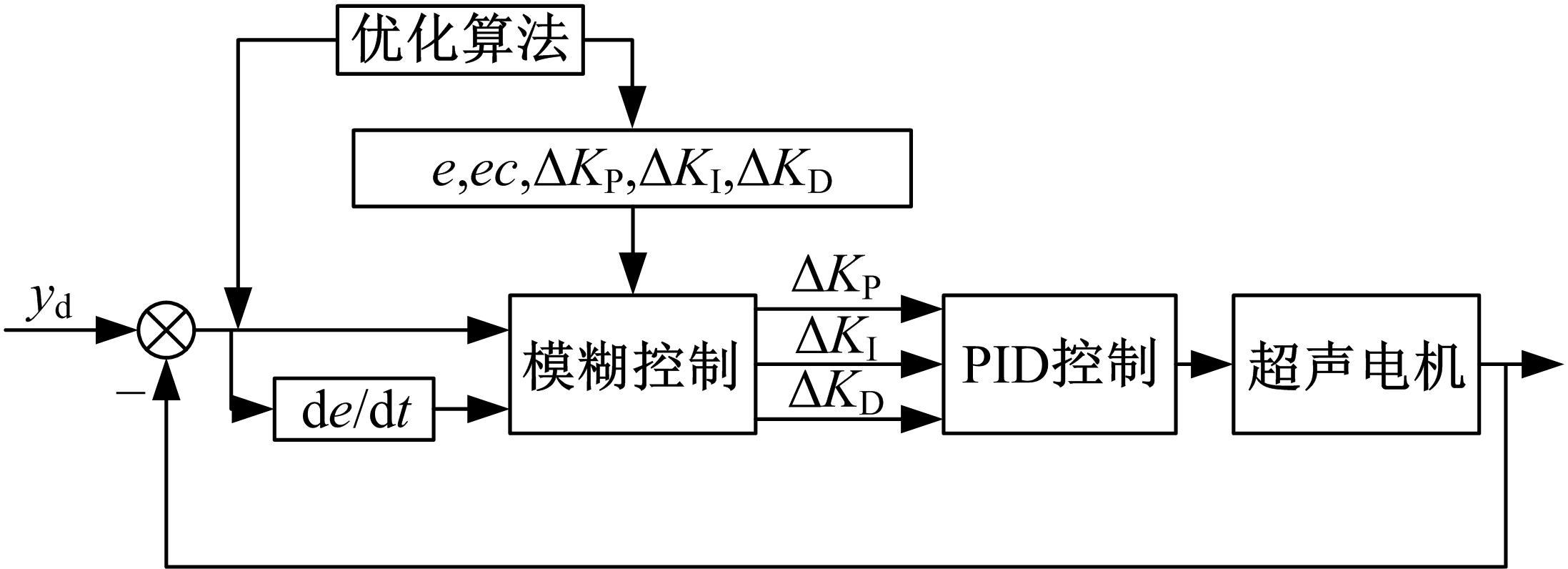
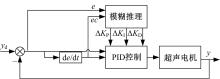
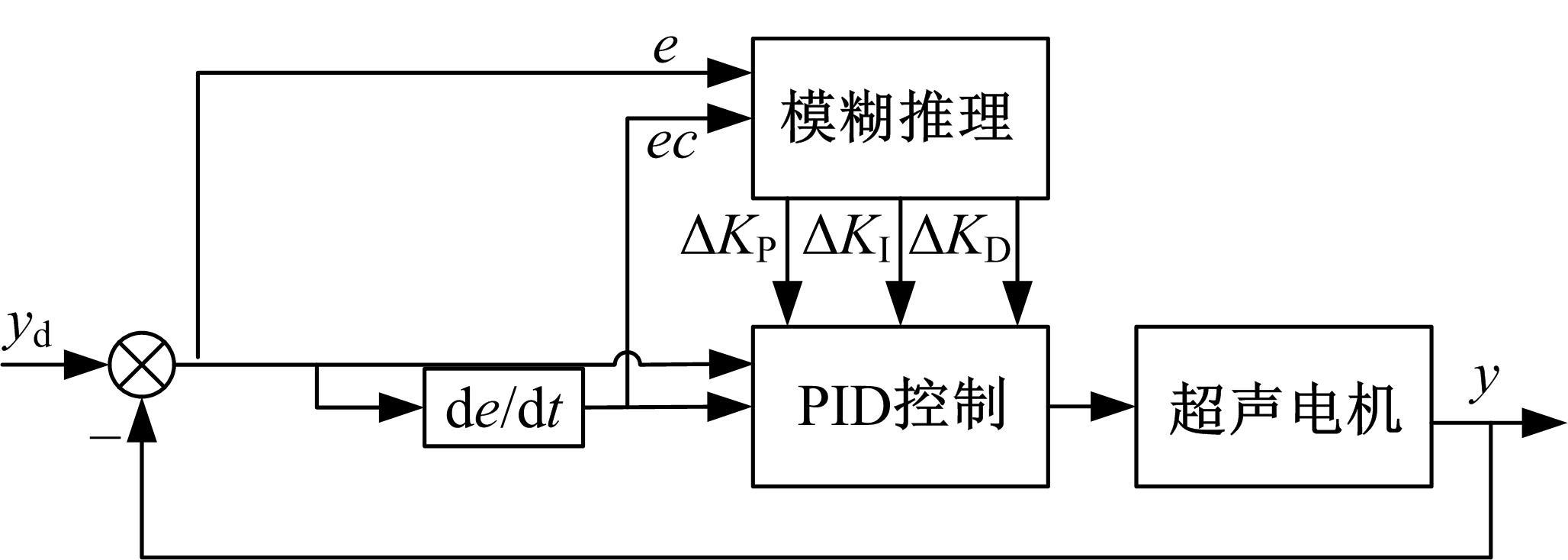
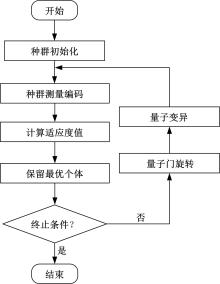
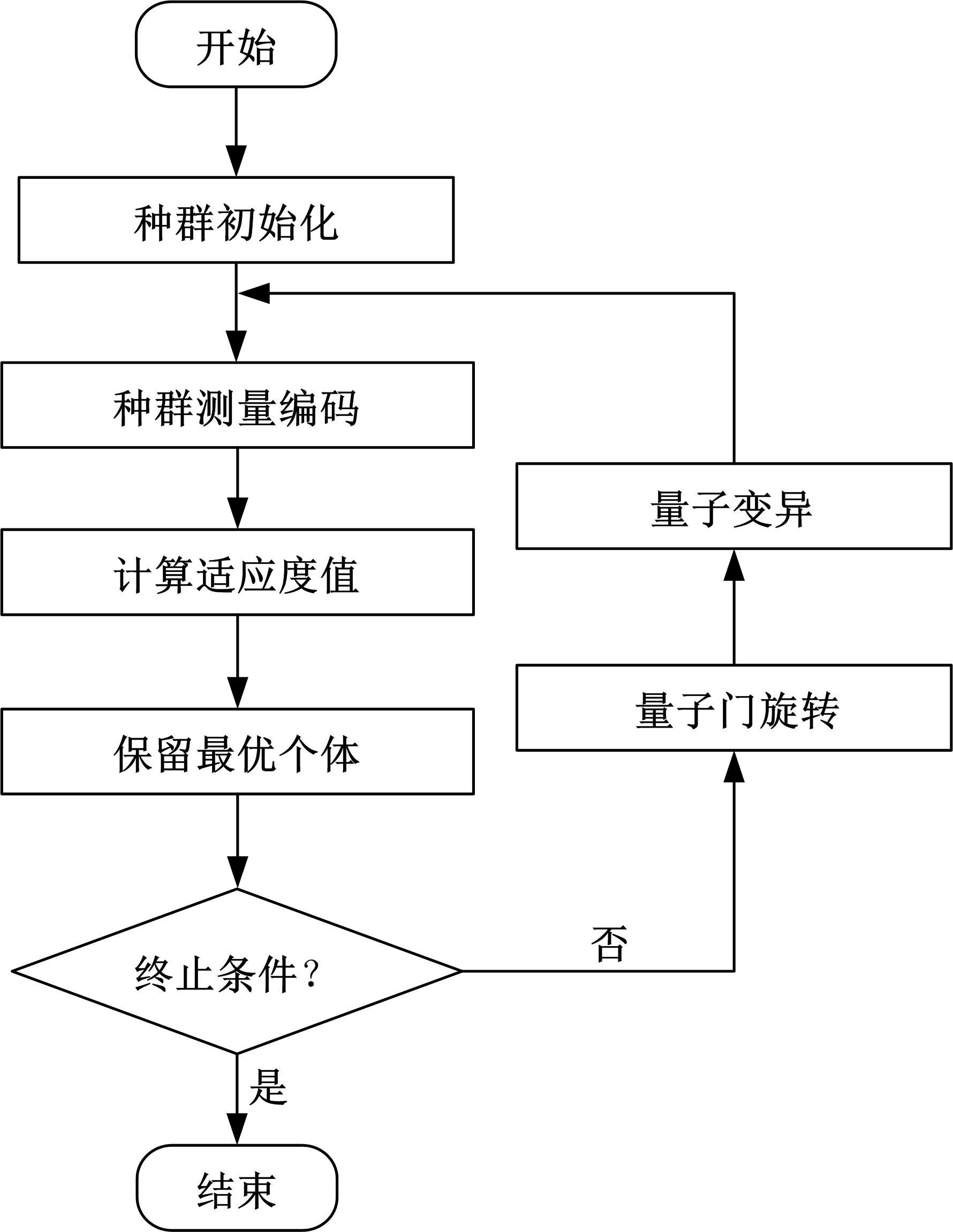
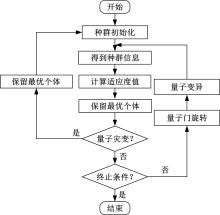
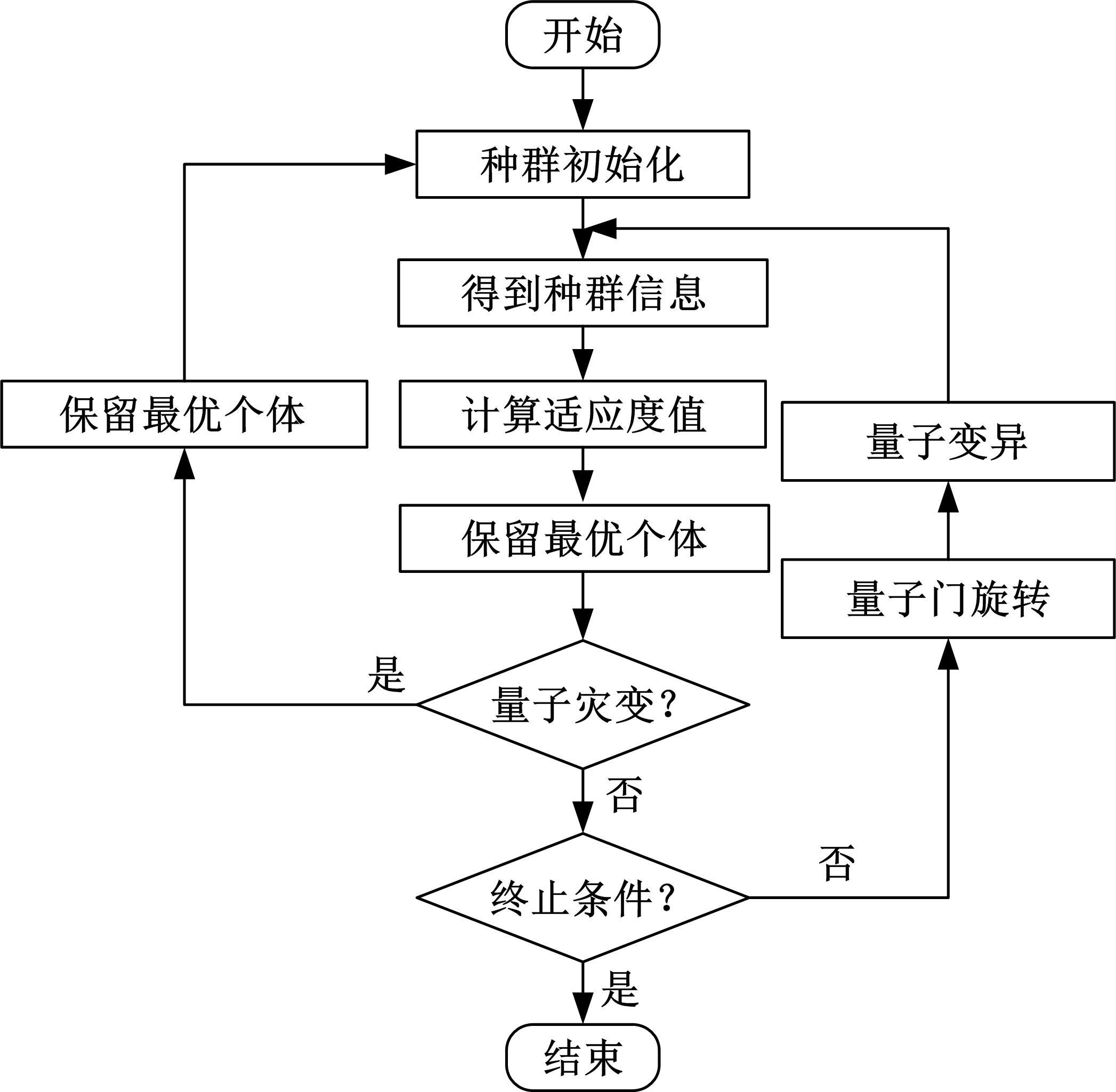
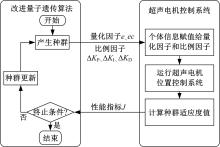
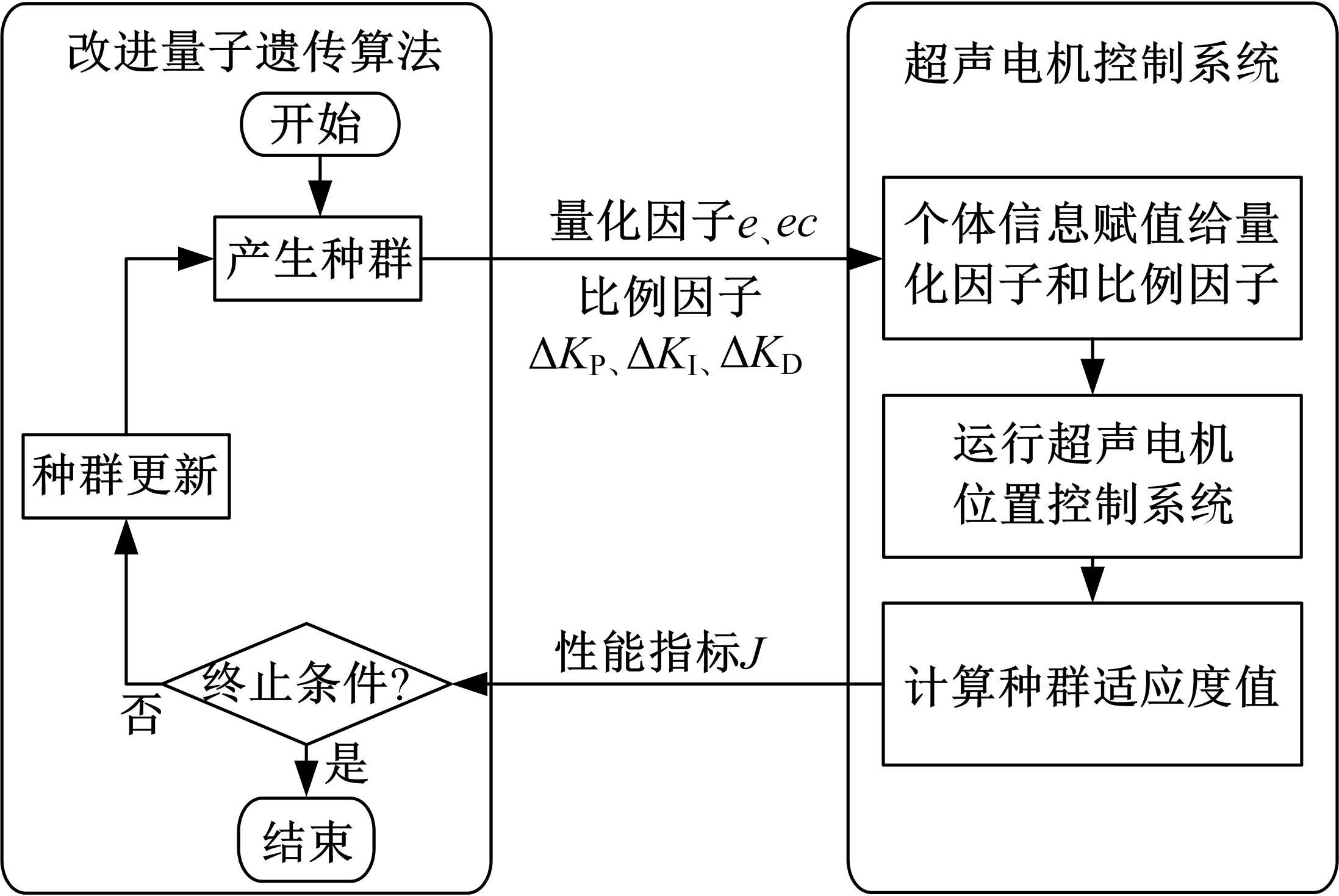
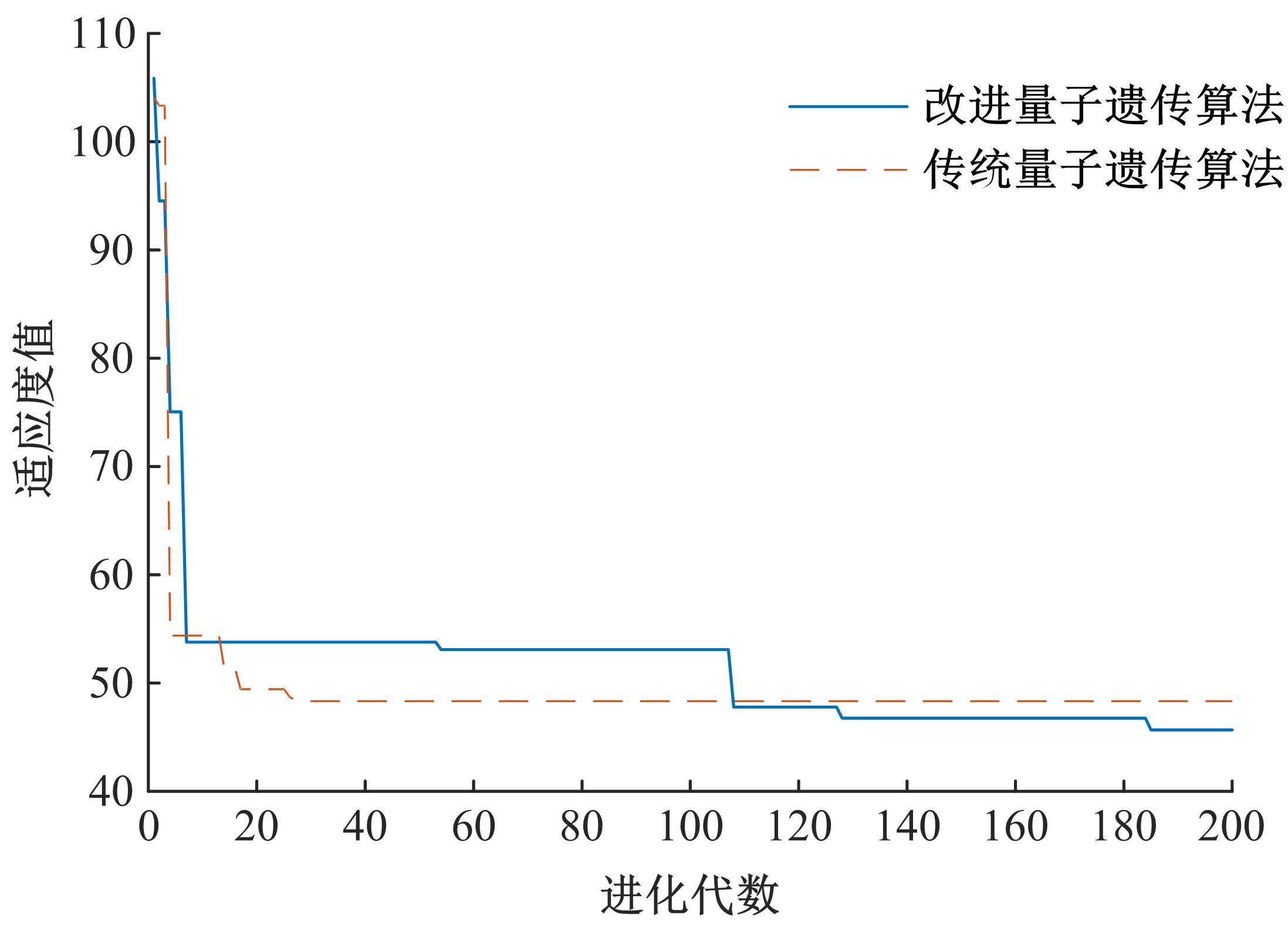
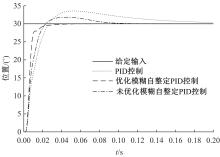
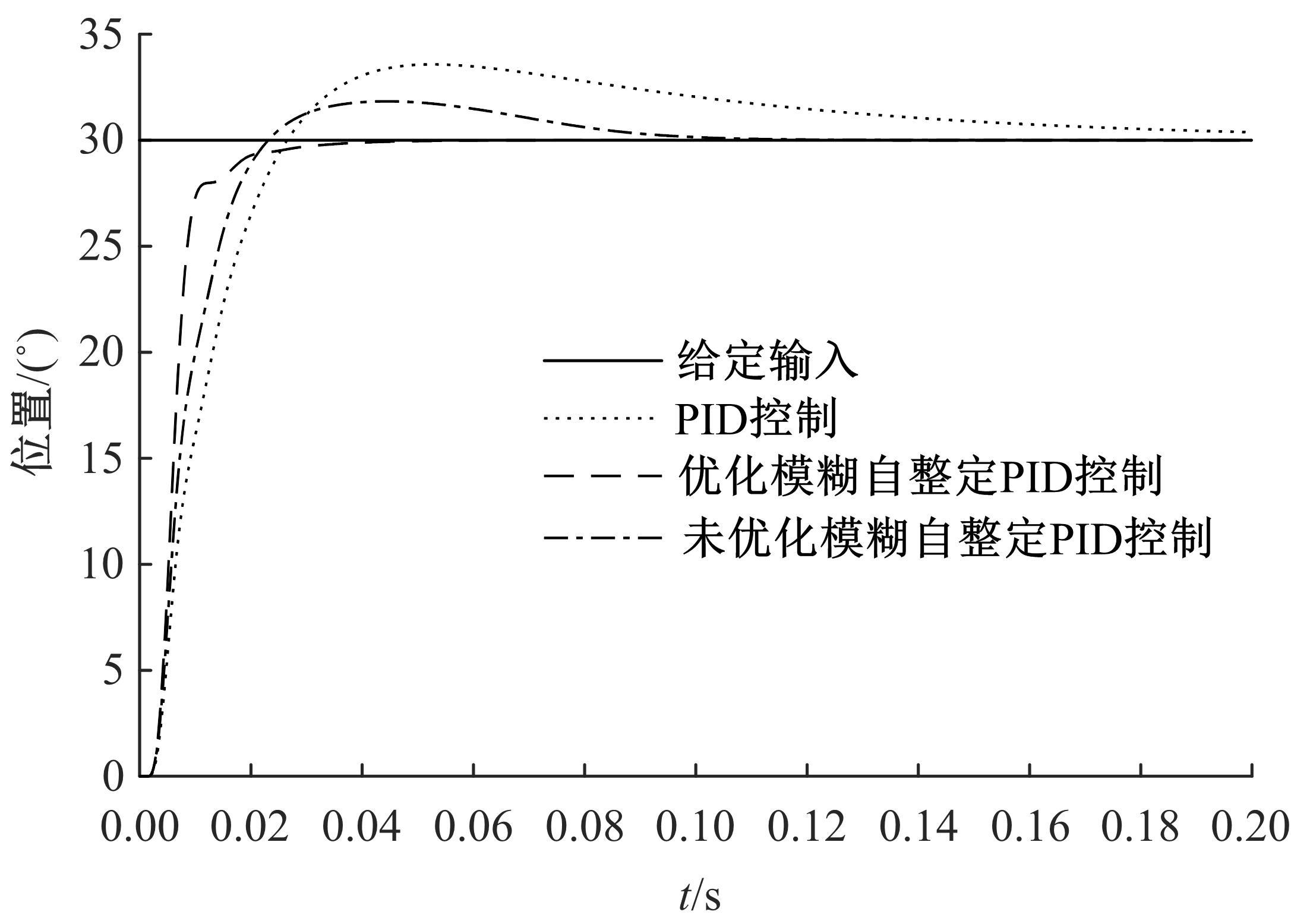
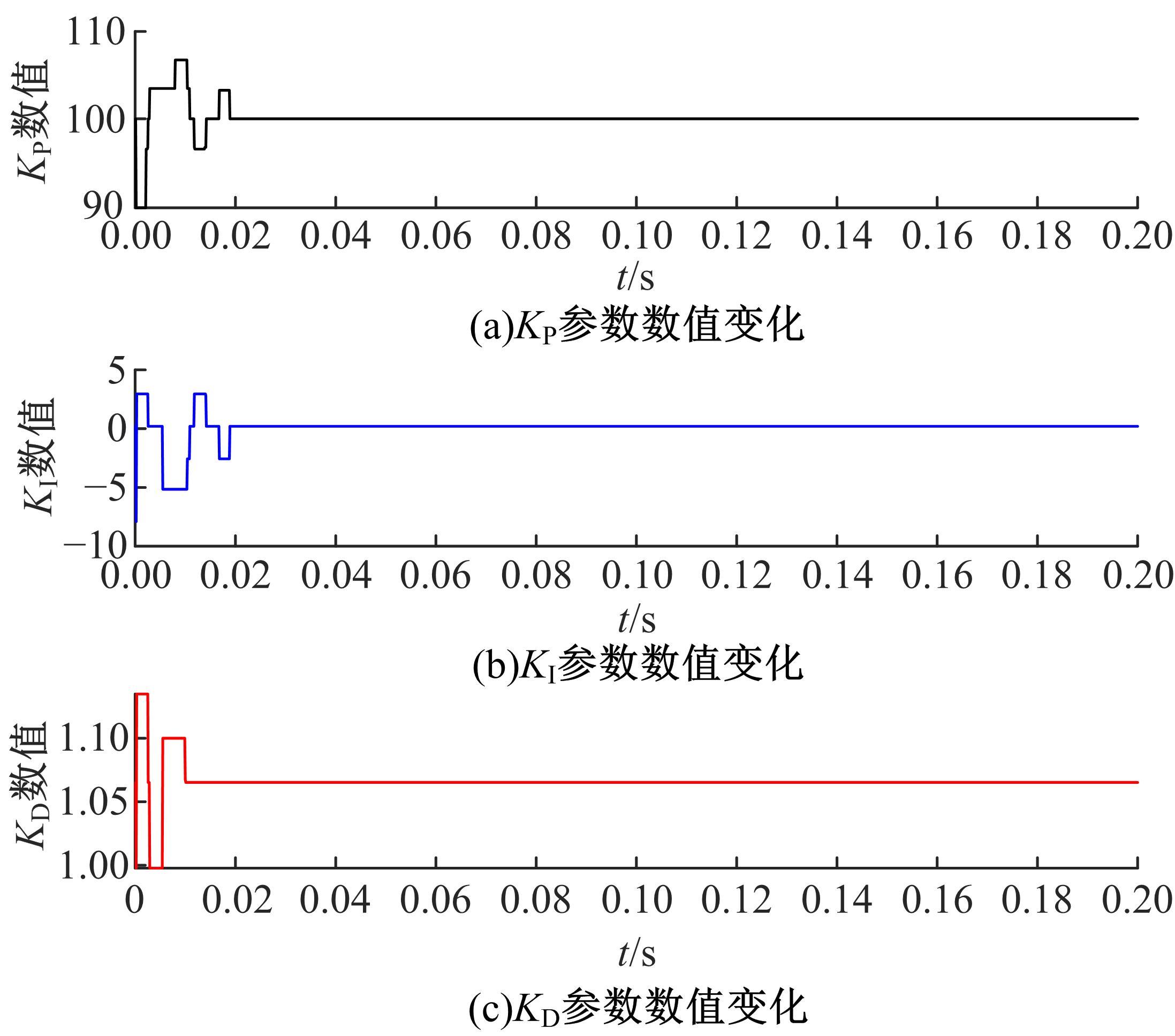
Journal of Jilin University(Engineering and Technology Edition) ›› 2021, Vol. 51 ›› Issue (6): 1990-1996.doi: 10.13229/j.cnki.jdxbgxb20200659
Fuzzy PID control of ultrasonic motor based on improved quantum genetic algorithm
Jian-xin FENG( ),Qiang WANG,Ya-lei WANG,Biao XU
),Qiang WANG,Ya-lei WANG,Biao XU
- Academy of Astronautics,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China
CLC Number:
- TP273
| 1 | 张俊峰. 直线超声电机建模仿真及驱动控制器设计[D]. 深圳: 哈尔滨工业大学深圳研究生院, 2014. |
| Zhang Jun-feng. Modeling simulation and driving controller design of linear ultrasonic motor[D]. Shenzhen: Shenzhen Graduate School, Harbin Institute of Technology, 2014. | |
| 2 | 李霞, 陈维山, 谢涛. 双锥面齿自支撑轴系行波超声电机设计与有限元分析[J]. 吉林大学学报:工学版, 2008, 38(4): 940-945. |
| Li Xia, Chen Wei-shan, Xie Tao. Finite element analysis and experiment on travelling-wave ultrasonic motor with two-sided cone-shaped teeth and half-supported shafting[J]. Journal of Jilin University(Engineering and Technology Edition), 2008, 38(4): 940-945. | |
| 3 | Wang Rui-qi, Li Ke, Cui Na-xin, et al. A new PID-type fuzzy neural network controller based on genetic algorithm with improved smith predictor[C]∥Proceedings of Joint 48th IEEE Conference on Decision and Control and 28th Chinese Control Conference, Shanghai, China, 2009:5708-5713. |
| 4 | 黄文文, 宋璐, 史敬灼. 超声波电机P型迭代学习转速控制[J]. 微电机, 2019, 52(6): 78-82. |
| Huang Wen-wen, Song Lu, Shi Jing-zhuo. P-type iterative learning speed control of ultrasonic motor[J]. Micromotors, 2019, 52(6): 78-82. | |
| 5 | 贺红林, 朱华, 赵淳生. 超声电机基于模糊PI技术的位置控制[J]. 机械科学与技术, 2006,25(5):603-607. |
| He Hong-lin, Zhu Hua, Zhao Chun-sheng. Position control of an ultrasonic motor using fuzzy PI technique[J]. Mechanical Science and Technology for Aerospace Engineering, 2006,25(5):603-607. | |
| 6 | 郑春娇, 朱延枫. 基于模糊PID的超声电机控制[J]. 辽宁工业大学学报:自然科学版, 2011, 31(2): 95-98. |
| Zhen Chun-jiao, Zhu Yan-feng. Control of ultrasonic motor based on fuzzy PID[J]. Journal of Liaoning University of Technology(Natural Science Edition), 2011, 31(2): 95-98. | |
| 7 | 孙晓明. 量子计算若干前沿问题综述[J]. 中国科学: 信息科学, 2016, 46(8): 982-1002. |
| Sun Xiao-ming. A survey of some frontier problems in quantum computing[J]. Scientia Sinica(Informationis), 2016, 46(8): 982-1002. | |
| 8 | 李静, 余春贤. 基于模糊与PID的车辆底盘集成控制系统[J]. 吉林大学学报:工学版, 2013,43():509-513. |
| Li Jing, Yu Chun-xian. Vehicle chassis integrated control system based on fuzzy and PID[J]. Journal of Jilin University(Engineering and Technology Edition), 2013,43(Sup.1):509-513. | |
| 9 | 陈垚彤. 基于优化问题的量子遗传算法研究[D]. 成都: 电子科技大学计算机科学与工程学院, 2019. |
| Chen Yao-tong. Research on quantum genetic algorithm based on timization problems[D]. Chengdu: School of Computer Science and Engineering, University of Electronic Science and Technology of China, 2019. | |
| 10 | 李士勇, 李盼池, 袁丽英. 量子遗传算法及在模糊控制器参数优化中的应用[J]. 系统工程与电子技术, 2007, 29(7): 1134-1138. |
| Li Shi-yong, Li Pan-chi, Yuan Li-ying. Quantum genetic algorithm with application in fuzzy controller parameter optimization[J]. Systems Engineering and Electronics, 2007, 29(7): 1134-1138. | |
| 11 | 王卫星. 基于改进鸡群算法的模糊PID控制器设计[J]. 自动化技术与应用, 2019, 38(9): 1-5. |
| Wang Wei-xing. Design of fuzzy PID controller based on improved chicken swarm algorithm[J]. Techniques of Automation and Applications, 2019, 38(9):1-5. | |
| 12 | 刘玉可, 史敬灼. 基于简化模糊规则的超声波电机模糊PI转速控制[J]. 电机技术, 2019,39(6): 16-19, 43. |
| Liu Yu-ke, Shi Jing-zhuo. Fuzzy PI speed control of the ultrasonic motor based upon simplified fussy rules[J]. Electrical Machinery Technology, 2019,39(6):16-19, 43. |
| [1] | Yan MA,Jian-fei HUANG,Hai-yan ZHAO. Method of vehicle formation control based on vehicle to vehicle communication [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(2): 711-718. |
| [2] | DENG Li-fei, SHI Yao-wu, ZHU Lan-xiang, YU Ding-li. Failure detection of closed-loop systems and application to SI engines [J]. 吉林大学学报(工学版), 2017, 47(2): 577-582. |
| [3] |
LI Xia1,2, CHEN Wei-shan1, XIE Tao1 .
Finite element analysis and experiment on travelling-wave ultrasonic motor with two-sided cone-shaped teeth and self-supported shafting [J]. 吉林大学学报(工学版), 2008, 38(04): 940-945. |
| [4] |
GE Hong-wei1,LI Xiao-lin2,LIANG Yan-chun3,HE Xiang-dong4 .
Immune PSO-based dynamic recurrent neural network for identifying and controlling nonlinear systems [J]. 吉林大学学报(工学版), 2008, 38(04): 858-864. |
|
||