移动装弹机械臂的逆运动学多种群灰狼算法求解方法

doi:10.13229/j.cnki.jdxbgxb.20230656

Abstract

Abstract:

Aiming at the problem that the inverse kinematics performance of the mobile loading manipulator needs to be improved， an inverse kinematics solution method based on the multi-population gray wolf algorithm is proposed. Firstly， the inverse kinematics problem of the mobile loading manipulator is transformed into an equivalent optimal problem， and the fitness function is established according to the optimization objective. Secondly， based on the gray wolf algorithm， the grey wolf population is expanded， the particle swarm algorithm and the position updating method of the optimal individual inverse guidance are introduced， and the random reorganization threshold elimination mechanism is set. Then， the algorithm is applied to iteratively invert so that the fitness function approaches 0 to obtain the inverse solution. 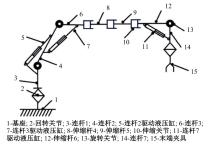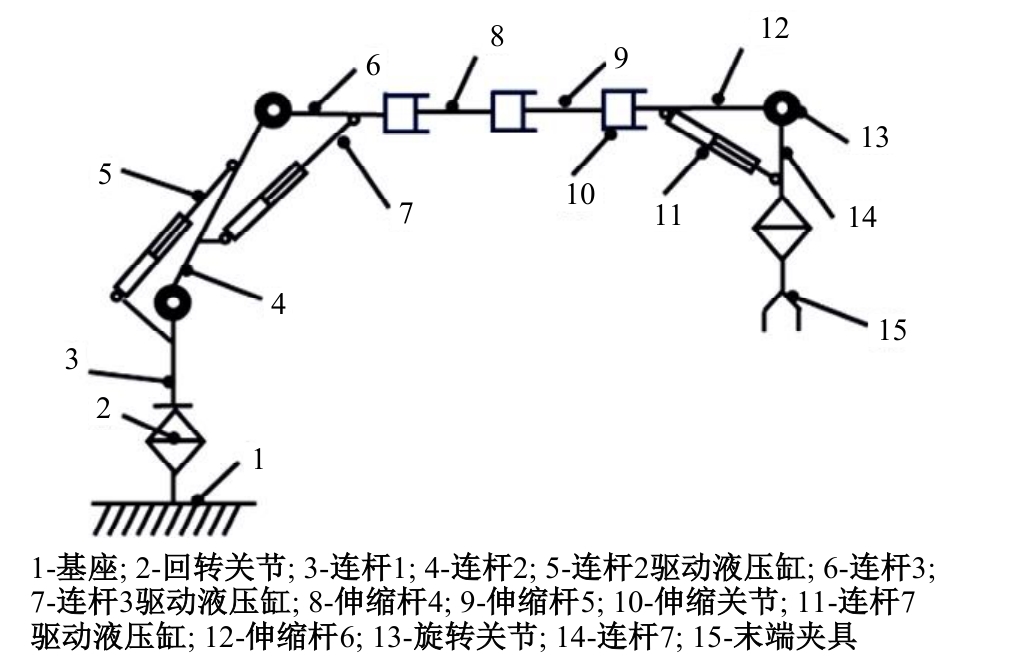Finally， the simulation comparison with other solving methods shows that the proposed method has better convergence， solution accuracy and repeatability.

Key words: control science and control engineering, mobile loading missile manipulator, kinematic inversion, multi-population grey wolf optimization algorithm, fitness function

CLC Number:

TP241

Yun-feng HU,Jia-min LI,Zhi-guo TANG. Solving method on inverse kinematics of mobile loading missile manipulator by multi-population grey wolf optimization algorithm[J].Journal of Jilin University(Engineering and Technology Edition), 2025, 55(4): 1443-1452.

Figures/Tables 15

Fig.1

Fig.2

Fig.3

Fig.4

Table 1

Parameters of mobile loading missile manipulator"

描述	符号	单位	数值
杆1长度	$l 1$	m	1.74
杆2长度	$l 2$	m	2.5
杆3长度	$l 3$	m	3
伸缩杆长度	$D$	m	1.5
连杆7长度	$l 7$	m	0.8
吊具长度	$l 8$	m	1.2

Table 1

Fig.5

Fig.6

Fig.7

Table 2

Test function"

测试函数	定义域	最小值
$f 1 x = ∑ i = 1 30 x i 2$	［-100，100］	0
$f 2 x = ∑ i = 1 30 x i + ? i = 1 30 x i$	［-10，10］	0
$f 3 x = ∑ i = 1 30 x i 2 - 10 c o s 2 π x i + 10$	［-5.12，5.12］	0
$f 4 x = - ∑ i = 1 4 c i ·$ $e x p - ∑ j = 1 3 a i j x j - p i j 2$	［1，3］	-3.86

Table 2

Fig.8

Table 3

Test function solving index statistics"

函数	算法	平均值	最优值	最差值	方差
F₁	GWO	$9.384 ? 6 × 10 - 9$	$6.885 ? 9 × 10 - 10$	$4.367 ? 6 × 10 - 8$	$8.728 ? 6 × 10 - 17$
F₁	MGWO	$5.894 ? 1 × 10 - 14$	$1.098 ? 8 × 10 - 14$	$1.755 ? 7 × 10 - 13$	$1.304 ? 5 × 10 - 27$
F₂	GWO	$6.755 ? 2 × 10 - 6$	$2.377 ? 7 × 10 - 6$	$1.861 ? 6 × 10 - 5$	$1.081 ? 1 × 10 - 11$
F₂	MGWO	$5.162 ? 6 × 10 - 9$	$2.010 ? 2 × 10 - 9$	$7.955 ? 5 × 10 - 9$	$1.804 ? 7 × 10 - 18$
F₃	GWO	$14.747 ? 9$	$7.767 ? 6 × 10 - 6$	33.462 2	60.446 2
F₃	MGWO	$1.304 ? 6$	$1.690 ? 0 × 10 - 10$	6.207 6	2.722 1
F₄	GWO	$- 3.860 ? 9$	$- 3.862 ? 8$	$0$	$7.197 ? 2 × 10 - 6$
F₄	MGWO	$- 3.862 ? 8$	$- 3.862 ? 8$	$0$	$3.592 ? 7 × 10 - 11$

Table 3

Fig.9

Fig.10

Table 4

Statistics of solving index by algorithm"

算法	平均值	最优值	最差值	方差
GWO	0.429 2	0.011 5	1.061 3	1.061 3
VAGWO	1.004 3	$8.036 ? 2 × 10 - 5$	6.205 3	6.205 3
PGWO	0.398 6	0.001 5	2.565 5	2.565 5
MGWO	0.012 2	0.006 4	0.022 6	$8.036 ? 2 × 10 - 5$

Table 4

Fig.11

References 14

[1]	霍希建, 刘伊威, 姜力,等. 具有关节限位的7R仿人机械臂逆运动学优化[J]. 吉林大学学报: 工学版, 2016, 46(1): 213-220.
	Huo Xi-jian, Liu Yi-wei, Jiang Li, et al. Inverse kinematics optimization of a 7R humanoid robot arm with joint limits [J]. Journal of Jilin University(Engineering and Technology Edition ), 2016, 46(1): 213-220.
[2]	石建平, 刘鹏, 陈冬云. 基于改进粒子群优化算法的冗余机械臂逆运动学求解[J]. 机械传动, 2021, 45(2): 69-75.
	Shi Jian-ping, Liu Peng, Chen Dong-yun. Inverse kinematics of redundant manipulator based on improved particle swarm optimization algorithm[J]. Journal of Mechanical Transmission, 2021, 45(2): 69-75.
[3]	冷舒, 吴克, 居鹤华. 机械臂运动学建模及解算方法综述[J]. 宇航学报, 2019, 40(11): 1262-1273.
	Leng Shu, Wu Ke, Ju He-hua, Kinematics modeling and calculating method of mechanical arm review [J]. Journal of Aerospace, 2019, 40(11): 1262-1273.
[4]	Alkayyali M, Tutunji T A. PSO-based algorithm for inverse kinematics solution of robotic arm manipulators[C]∥20th International Conference on Research and Education in Mechatronics (REM),IEEE, Wels, Austria, 2019: 1-6.
[5]	Ghosh A, Singh O, Ray A K. Inverse kinematic solution of a 7 DOF robotic manipulator using boundary restricted particle swarm optimization[J]. IFAC-PapersOnLine, 2022, 55(1): 101-105.
[6]	Liu Y, Xi J, Bai H, et al. A general robot inverse kinematics solution method based on improved PSO algorithm[J]. IEEE Access, 2021, 9: 32341-32350.
[7]	Gao R. Inverse kinematics solution of robotics based on neural network algorithms[J]. Journal of Ambient Intelligence and Humanized Computing, 2020, 11(12): 6199-6209.
[8]	Nguyen T, Bui T, Pham H. Using proposed optimization algorithm for solving inverse kinematics of human upper limb applying in rehabilitation robotic[J]. Artificial Intelligence Review, 2022, 55(1): 679-705.
[9]	Ahmed E S, Elhosseini M A, Haikal A Y. A new ABC variant for solving inverse kinematics problem in 5 DOF robot arm[J]. Applied Soft Computing, 2018, 73: 24-38.
[10]	杨凯, 黄晋英. 一种8自由度空间机械臂运动学及工作空间分析[J]. 机械传动, 2021, 45(3): 147-152.
	Yang Kai, Huang Jin-ying. Kinematics and workspace analysis of a 8-DOF space manipulator[J]. Mechanical Transmission, 2021, 45(3): 147-152.
[11]	张清松, 段帅臣, 夏热. 基于Matlab的拟人机械臂工作空间分析及仿真[J]. 机械传动, 2020, 44(12): 99-105.
	Zhang Qing-song, Duan Shuai-chen, Xia Re. Workspace analysis and simulation of anthropomorphic robotic arm based on Matlab[J]. Mechanical Transmission, 2020, 44(12): 99-105.
[12]	Mirjalili S, Mirjalili S M, Lewis A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46-61.
[13]	张晓凤, 王秀英. 灰狼优化算法研究综述[J]. 计算机科学, 2019, 46(3): 30-38.
	Zhang Xiao-feng, Wang Xiu-ying, Review of grey wolf optimization algorithm[J]. Computer Science, 2019, 46(3): 30-38.
[14]	Rezaei F, Safavi H R, Abd Elaziz M, et al. An enhanced grey wolf optimizer with a velocity-aided global search mechanism[J]. Mathematics, 2022, 10(3):No.351.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

Comments

Recommended 10

[1]	LI Shoutao, LI Yuanchun. Autonomous Mobile Robot Control Algorithm Based on Hierarchical Fuzzy Behaviors in Unknown Environments[J]. 吉林大学学报(工学版), 2005, 35(04): 391 -397 .
[2]	Liu Qing-min，Wang Long-shan，Chen Xiang-wei，Li Guo-fa. Ball nut detection by machine vision[J]. 吉林大学学报(工学版), 2006, 36(04): 534 -538 .
[3]	Li Hong-ying; Shi Wei-guang;Gan Shu-cai. Electromagnetic properties and microwave absorbing property of Z type hexaferrite Ba_3-xLa_xCo₂Fe₂₄O₄₁[J]. 吉林大学学报(工学版), 2006, 36(06): 856 -0860 .
[4]	Yang Shu-kai, Song Chuan-xue, An Xiao-juan, Cai Zhang-lin . Analyzing effects of suspension bushing elasticity on vehicle yaw response character with virtual prototype method[J]. 吉林大学学报(工学版), 2007, 37(05): 994 -0999 .
[5]	. [J]. 吉林大学学报(工学版), 2007, 37(06): 1284 -1287 .
[6]	Che Xiang-jiu，Liu Da-you，Wang Zheng-xuan . Construction of joining surface with G¹ continuity for two NURBS surfaces[J]. 吉林大学学报(工学版), 2007, 37(04): 838 -841 .
[7]	Liu Han-bing, Jiao Yu-ling, Liang Chun-yu,Qin Wei-jun . Effect of shape function on computing precision in meshless methods[J]. 吉林大学学报(工学版), 2007, 37(03): 715 -0720 .
[8]	Zhang Quan-fa，Li Ming-zhe，Sun Gang，Ge Xin . Comparison between flexible and rigid blank-holding in multi-point forming[J]. 吉林大学学报(工学版), 2007, 37(01): 25 -30 .
[9]	. [J]. 吉林大学学报(工学版), 2007, 37(04): 0 .
[10]	Li Yue-ying，Liu Yong-bing，Chen Hua . Surface hardening and tribological properties of a cam materials[J]. 吉林大学学报(工学版), 2007, 37(05): 1064 -1068 .

Solving method on inverse kinematics of mobile loading missile manipulator by multi-population grey wolf optimization algorithm

RICH HTML

PDF (PC)

Abstract

Cite this article

share this article

Figures/Tables 15

References 14

Related Articles 1

Metrics

Comments

Recommended 10