Journal of Jilin University(Engineering and Technology Edition) ›› 2020, Vol. 50 ›› Issue (1): 324-332.doi: 10.13229/j.cnki.jdxbgxb20181228
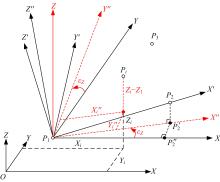
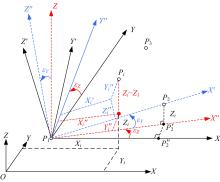
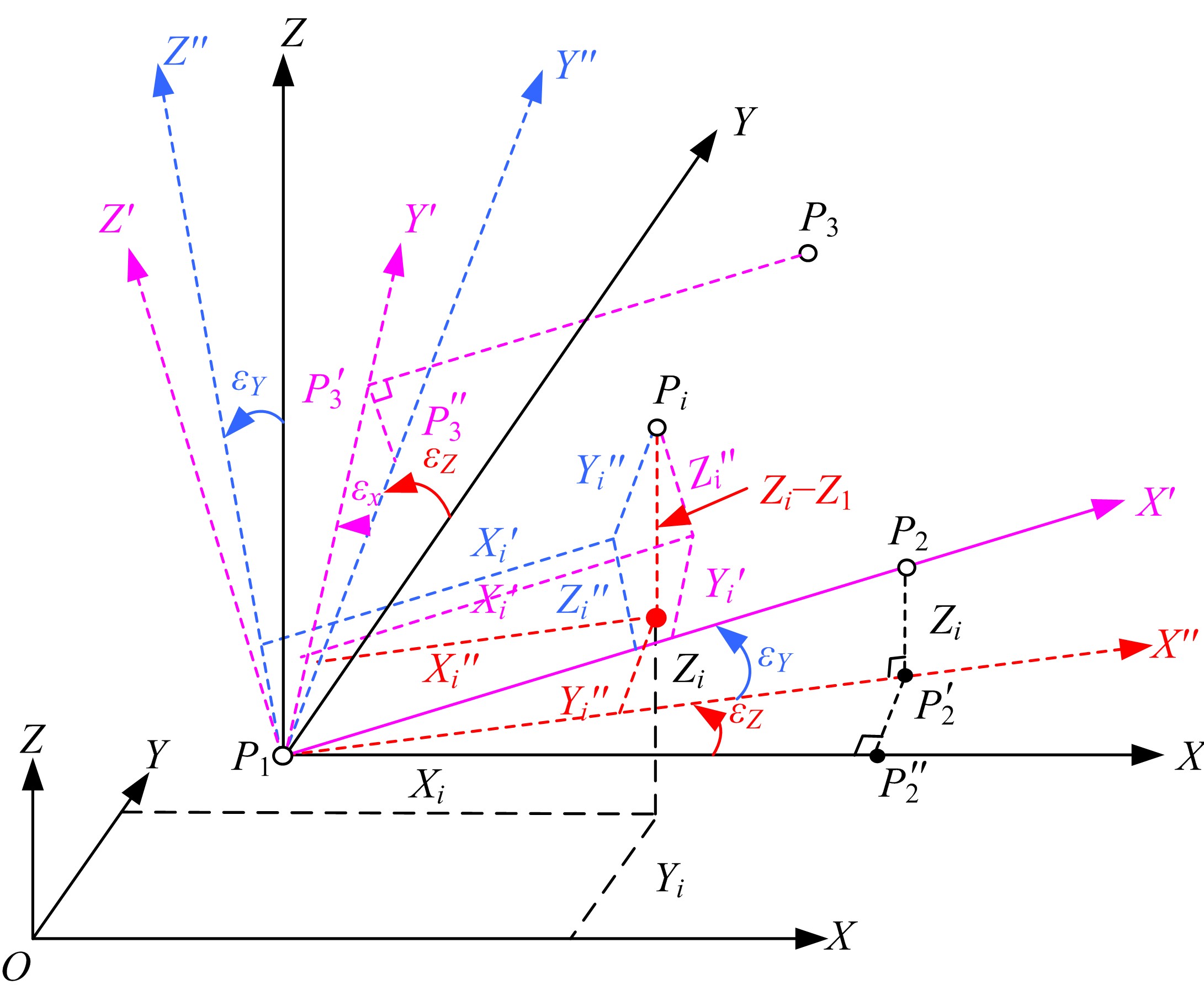
Universal three-point model of generating a new coordinate system and its application
Feng-yan WANG1( ),Xue-xin YAN2,Ming-chang WANG1,Xu-qing ZHANG1,Xue-feng NIU1,Qing WANG3(
),Xue-xin YAN2,Ming-chang WANG1,Xu-qing ZHANG1,Xue-feng NIU1,Qing WANG3( )
)
- 1. College of Geo?Exploration Science and Technology, Jilin University, Changchun 130026, China
2. Key Laboratory of Land Subsidence Monitoring and Prevention, Ministry of Natural Resources,Shanghai Institute of Geological Survey, Shanghai 200072,China
3. College of Construction Engineering, Jilin University, Changchun 130026, China
CLC Number:
- TP391
| 1 | Alashaikh A H. Numerical transformation technique for coordinate systems in the Kingdom of Saudi Arabia[J]. Arabian Journal of Geosciences, 2017, 10(6): 2903-2908. |
| 2 | 朱振宇, 江国焰, 王永明. 工业测量系统自由坐标系建立方法研究[J]. 矿山测量, 2009(5): 63-69. |
| Zhu Zhen-yu, Jiang Guo-yan, Wang Yong-ming. Study on the establishment of free-coordinate system of industrial measurement system[J]. Mine Surveying, 2009(5): 63-66, 69. | |
| 3 | 黄鹏, 王青, 李江雄, 等. 激光跟踪仪三维坐标转换综合优化方法[J]. 计算机集成制造系统, 2015, 21(11): 2912-2920. |
| Huang Peng, Wang Qing, Li Jiang-xiong, et al. Comprehensive optimization for three-dimensional coordinate transformation of laser tracker[J]. Computer Integrated Manufacturing System, 2015, 21(11): 2912-2920. | |
| 4 | Wang F, Wei X Z, and Li X. Coordinates transformation and the accuracy analysis in sensor network[J]. Journal of Systems Engineering and Electronics, 2005, 27(7): 1231-1234. |
| 5 | 孔祥元, 郭际明. 控制测量学[M]. 武汉: 武汉大学出版社, 2006. |
| 6 | 杨凡, 李广云, 王力. 三维坐标转换方法研究[J]. 测绘通报, 2010(6): 5-7, 15. |
| Yang Fan, Li Guang-yun, Wang Li. Research on the methods of calculating 3D coordinate transformation parameters[J]. Bulletin of Surveying and Mapping, 2010(6): 5-7, 15. | |
| 7 | 曾文宪, 陶本藻. 三维坐标转换的非线性模型[J]. 武汉大学学报:信息科学版, 2003, 28(5): 566-568. |
| Zeng Wen-xian, Tao Ben-zao. Non-linear adjustment model of three-dimensional coordinate transformation[J]. Geomatics and Information Science of Wuhan University, 2003, 28(5): 566-568. | |
| 8 | 潘国荣, 周莹, 张德海. 坐标转换模型在盾构姿态计算中的应用[J]. 大地测量与地球动力学, 2006, 26(3): 84-87. |
| Pan Guo-rong, Zhou Ying, Zhang De-hai. 3D datum transformation model for determining orientation of shield in subway construction[J]. Journal of Geodesy and Geodynamics, 2006, 26(3): 84-87. | |
| 9 | 赵思齐. 用于沉管施工的实时定位系统开发及应用[D].上海:同济大学土木工程学院, 2007. |
| Zhao Si-qi. Realtime positioning system in surveying of immersed tube[D]. Shanghai: College of Civil Engineering,Tongji University, 2007. | |
| 10 | 张凯, 单甘霖, 陈海, 等. 基于几何解算的飞机三维姿态测量方法[J]. 火力与指挥控制, 2012, 37(7): 43-46. |
| Zhang Kai, Shan Gan-lin, Chen Hai, et al. Measurement of aircraft’s 3D pose based on geometric algorithms[J]. Fire Control & Command Control, 2012, 37(7): 43-46. | |
| 11 | 刘志平, 杨磊. 大旋转角的空间直角坐标转换方法的改进[J]. 大地测量与地球动力学, 2016, 36(7): 586-590. |
| Liu Zhi-ping, Yang Lei. An improved method for spatial rectangular coordinate transformation with big rotation angle[J]. Journal of Geodesy and Geodynamics, 2016, 36(7): 586-590. | |
| 12 | 潘国荣, 汪大超, 周跃寅. 两种大转角空间坐标转换模型研究[J]. 山东科技大学学报:自然科学版, 2015, 34(1): 61-67. |
| Pan Guo-rong, Wang Da-chao, Zhou Yue-yin. Two spatial coordinate transformation model of large angle[J]. Journal of Shandong University of Science and Technology (Natural Science), 2015, 34(1): 61-67. | |
| 13 | 陈义, 沈云中, 刘大杰. 适用于大旋转角的三维基准转换的一种简便模型[J]. 武汉大学学报:信息科学版, 2004, 29(12): 1101-1105. |
| Chen Yi, Shen Yun-zhong, Liu Da-jie. A simplified model of three dimensional-datum transformation adapted to big rotation angle[J]. Geomatics and Information Science of Wuhan University, 2004, 29(12): 1101-1105. | |
| 14 | Wu Y, Liu J, and Ge H Y. Comparison of total least squares and least squares for four-and seven-parameter model coordinate transformation[J]. Journal of Applied Geodesy, 2016, 10(4): 259-266. |
| 15 | 李新友, 陈五一. 基于奇异值分解的刚体位姿误差检测方法[J]. 计算机集成制造系统, 2011, 17(9): 1981-1987. |
| Li Xin-you, Chen Wu-yi. Detection of pose errors for a rigid body based on singular value decomposition method[J]. Computer Integrated Manufacturing Systems, 2011, 17(9): 1981-1987. | |
| 16 | 叶锃锋, 冯恩信. 基于四元数和卡尔曼滤波的两轮车姿态稳定方法[J]. 传感器学报, 2012, 25(4): 524-528. |
| Ye Zeng-feng, Feng En-xin. Attitude stabilization based on quaternion and Kalman filter for two-wheeled vehicle[J]. Chinese Journal of Sensors and Actuators, 2012, 25(4): 524-528. | |
| 17 | 姚吉利, 韩保民, 杨元喜. 罗德里格矩阵在三维坐标转换严密解算中的应用[J]. 武汉大学学报:信息科学版, 2006, 31(12): 1094-1096, 1119. |
| Yao Ji-li, Han Bao-min, Yang Yuan-xi. Applications of Rodrigue matrix in 3D coordinate transformation[J]. Geomatics and Information Science of Wuhan University, 2006, 31(12): 1094-1096, 1119. | |
| 18 | 张正禄. 工程测量学[M]. 武汉:武汉大学出版社, 2005. |
| 19 | 冯文灏. 工业测量中标准尺的几种应用[J]. 测绘通报, 2003(3): 40-43. |
| Feng Wen-hao. Some applications of standard rulers in industrial surveying[J]. Bulletin of Surveying and Mapping, 2003(3): 40-43. | |
| 20 | 武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 武汉:武汉大学出版社, 2011. |
| 21 | 王凤艳, 黄润秋, 陈剑平, 等. 基于计算机视觉和测量平差理论的相机标定[J]. 吉林大学学报:工学版, 2017, 47(3): 944-951. |
| Wang Feng-yan, Huang Run-qiu, Chen Jian-ping, et al. Camera calibration based on computer vision and surveying adjustment fundamentals[J]. Journal of Jilin University (Engineering and Technology Edition), 2017, 47(3): 944-951. | |
| 22 | 吉林大学. 数码相机标定及影像校正系统Camera Calibration 1.0[P]. 中国: 2012SR039020, 2012-03-09. |
| [1] | Tie-jun WANG,Wei-lan WANG. Thangka image annotation based on ontology [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(1): 289-296. |
| [2] | Xiao-hui WANG,Lu-shen WU,Hua-wei CHEN. Denoising of scattered point cloud data based on normal vector distance classification [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(1): 278-288. |
| [3] | Hong-yan WANG,He-lei QIU,Jia ZHENG,Bing-nan PEI. Visual tracking method based on low⁃rank sparse representation under illumination change [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(1): 268-277. |
| [4] | Xiong-fei LI,Jing WANG,Xiao-li ZHANG,Tie-hu FAN. Multi-focus image fusion based on support vector machines and window gradient [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(1): 227-236. |
| [5] | Xiang-jiu CHE,Hua-luo LIU,Qing-bin SHAO. Fabric defect recognition algorithm based onimproved Fast RCNN [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(6): 2038-2044. |
| [6] | Hong-wei ZHAO,Peng WANG,Li-li FAN,Huang-shui HU,Ping-ping LIU. Similarity retention instance retrieval method [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(6): 2045-2050. |
| [7] | Bing-hai ZHOU,Qiong WU. Balancing and optimization of robotic assemble lines withtool and space constraint [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(6): 2069-2075. |
| [8] | Hong-wei ZHAO,Ming-zhao LI,Jing LIU,Huang-shui HU,Dan WANG,Xue-bai ZANG. Scene classification based on degree of naturalness and visual feature channels [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(5): 1668-1675. |
| [9] | Bin LI,Xu ZHOU,Fang MEI,Shuai-ning PAN. Location recommendation algorithm based on K-means and matrix factorization [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(5): 1653-1660. |
| [10] | Yan-jun SUN,Xuan-jing SHEN,Hai-peng CHEN,Yong-zhe ZHAO. Recaptured image forensics algorithm based on local plane linear point [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(4): 1320-1328. |
| [11] | Xiong-fei LI,Lu SONG,Xiao-li ZHANG. Remote sensing image fusion based on cooperative empirical wavelet transform [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(4): 1307-1319. |
| [12] | Feng⁃wen ZHAI,Jian⁃wu DANG,Yang⁃ping WANG,Jing JIN,Wei⁃wei LUO. Extended contour⁃based fast affine invariant feature extracting [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(4): 1345-1356. |
| [13] | Yuan-ning LIU,Shuai LIU,Xiao-dong ZHU,Guang HUO,Tong DING,Kuo ZHANG,Xue JIANG,Shu-jun GUO,Qi-xian ZHANG. Iris secondary recognition based on decision particle swarm optimization and stable texture [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(4): 1329-1338. |
| [14] | Zhi⁃hui LI,Tao ZHONG,Yong⁃hua ZHAO,Yong⁃li HU,Hai⁃tao LI,Jing⁃wei ZHAO. Pedestrian tracking algorithm for autonomous driving [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(3): 680-687. |
| [15] | Dan⁃tong OUYANG,Jun XIAO,Yu⁃xin YE. Distant supervision for relation extraction with weakconstraints of entity pairs [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(3): 912-919. |
|
||