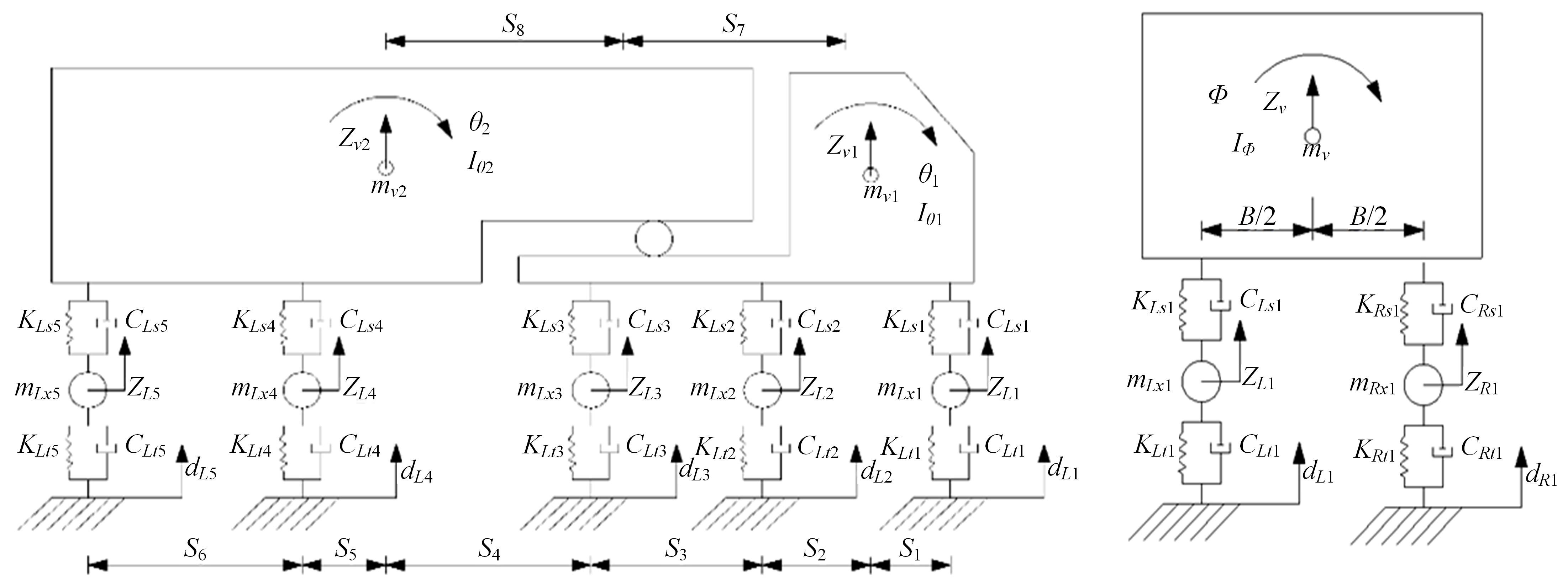
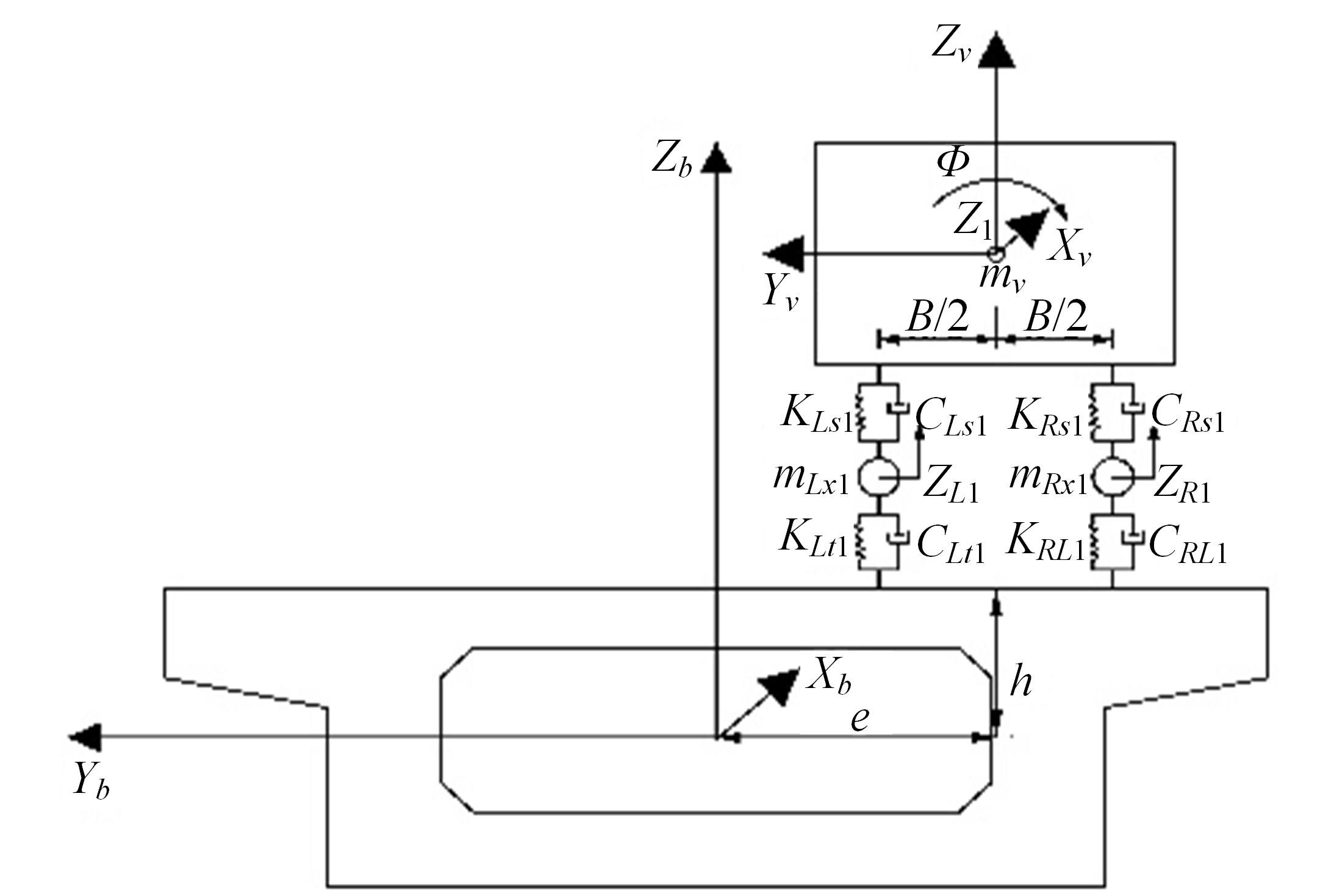
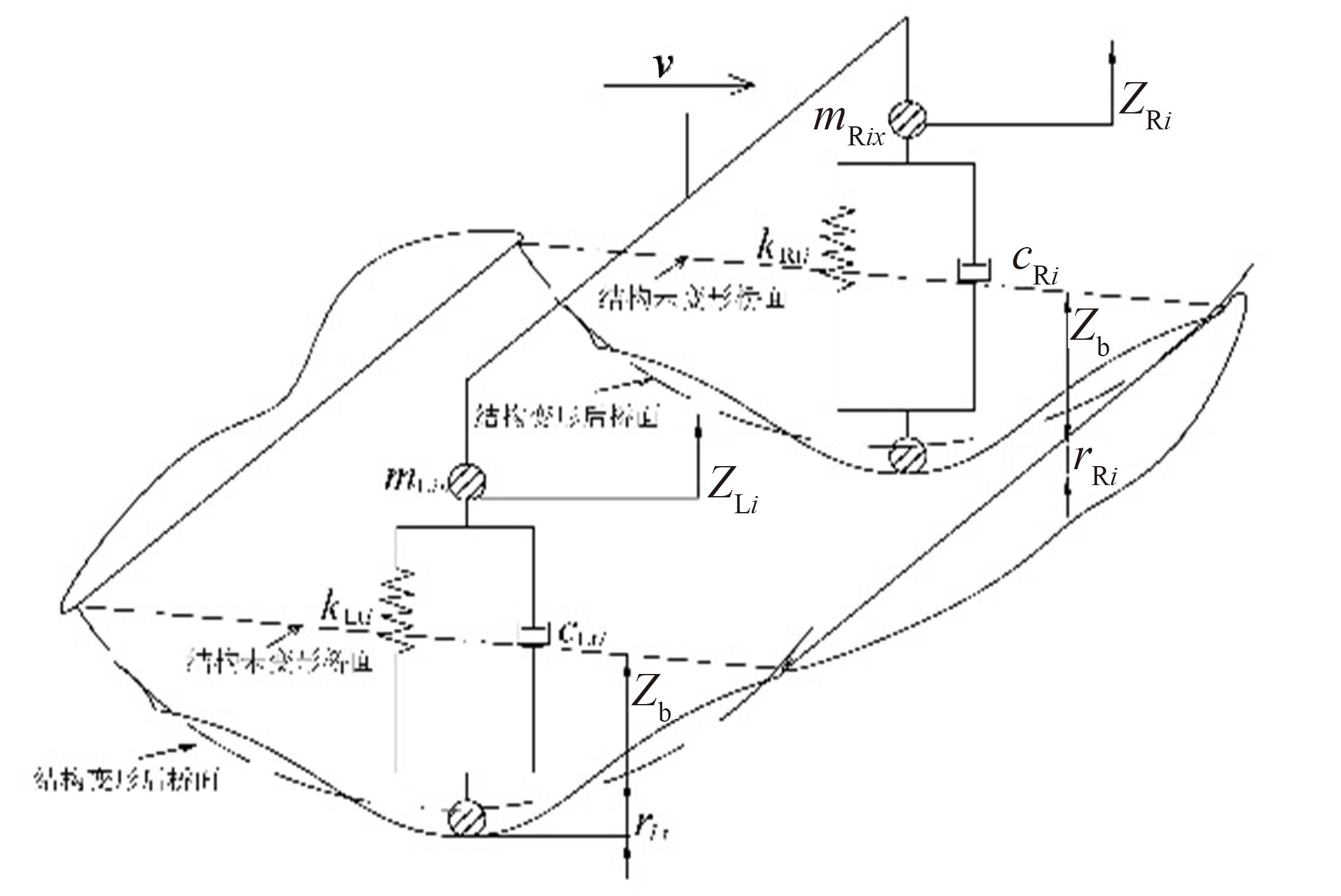
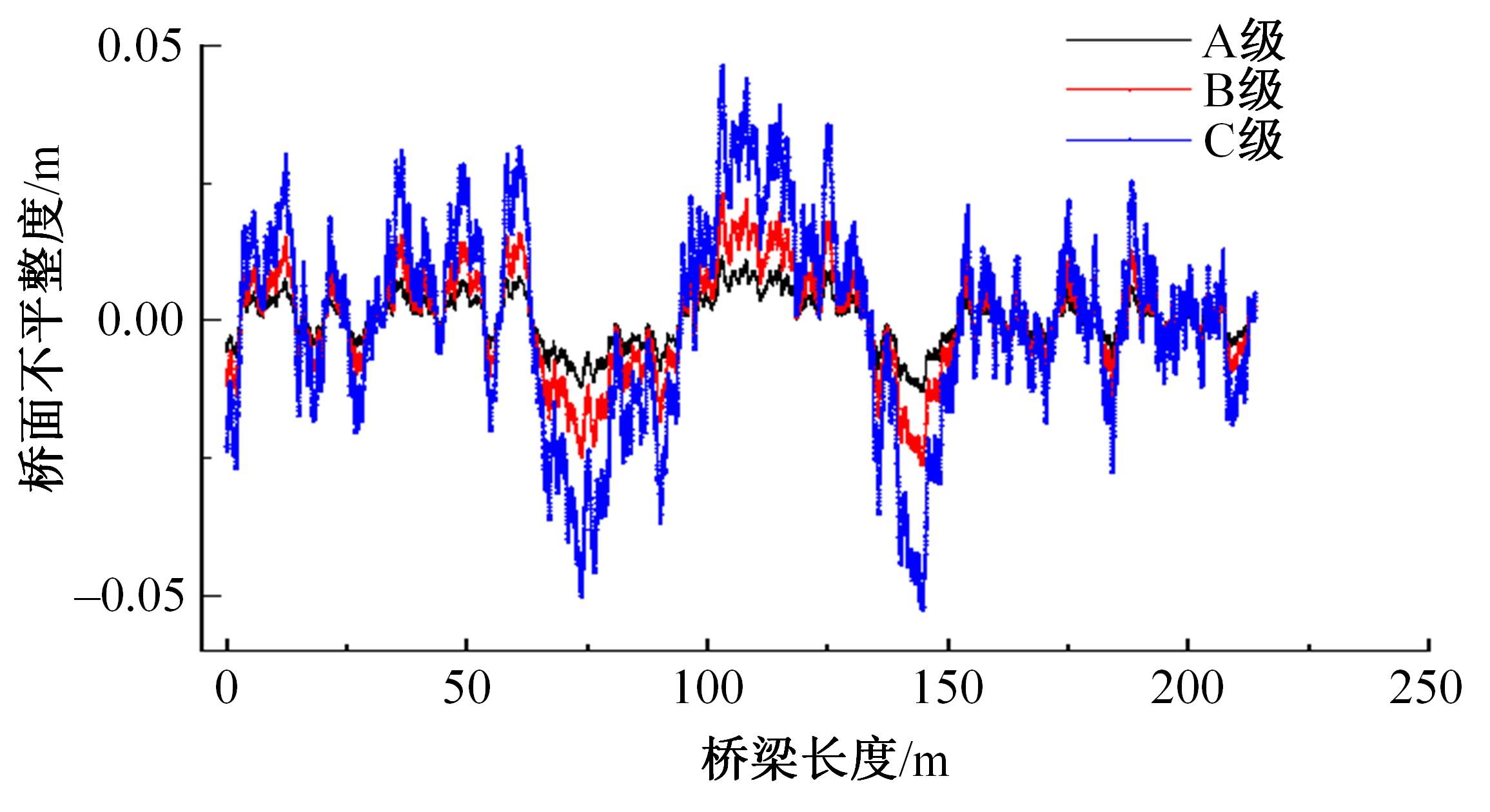
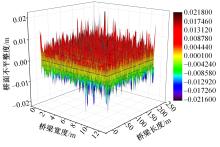
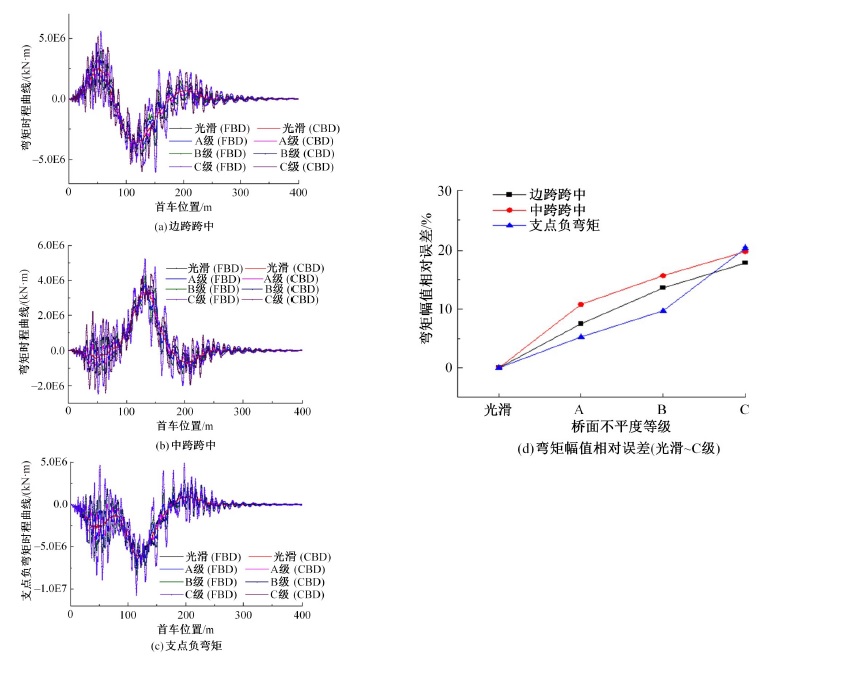
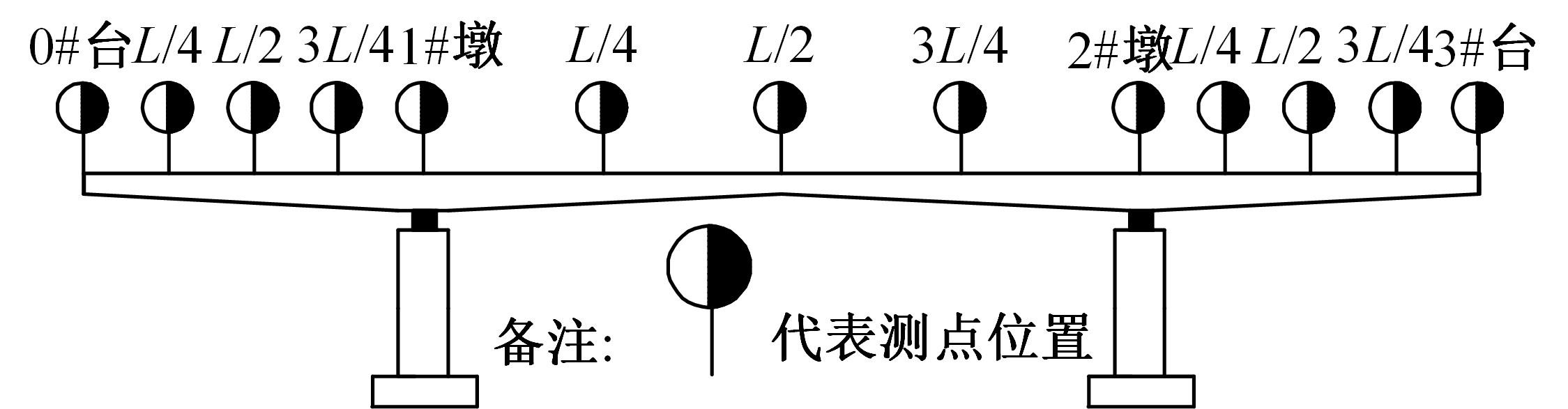
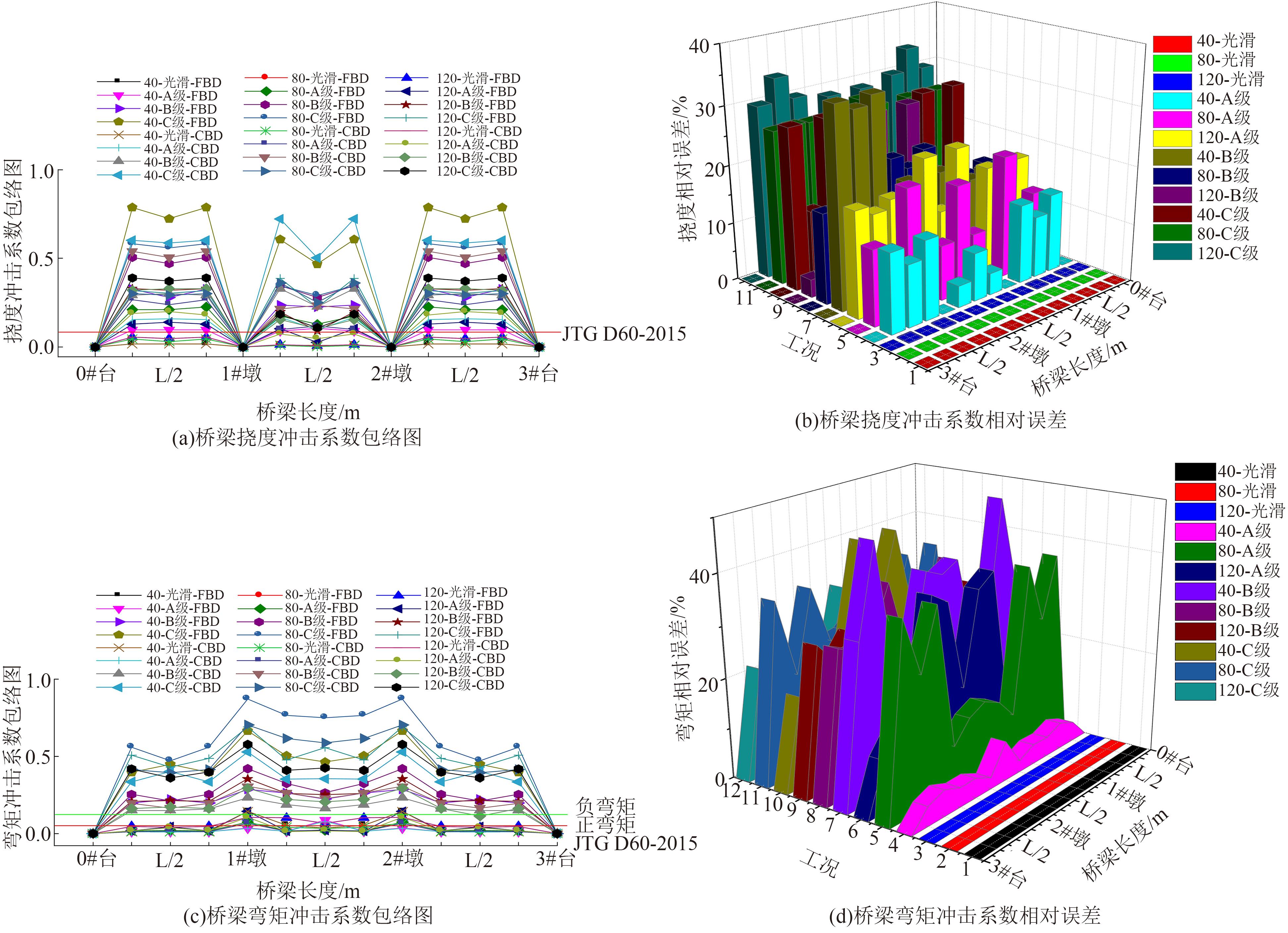
Journal of Jilin University(Engineering and Technology Edition) ›› 2024, Vol. 54 ›› Issue (2): 436-444.doi: 10.13229/j.cnki.jdxbgxb.20220400

Previous Articles    

Vibration response of continuous girder bridge based on wheel⁃deck coherent excitation

Zhi-qiang HAN1(),Gang XIE2(),Ya-juan ZHUO1,Zuo-long LUO3,Hua-teng LI1   

  1. 1.School of Transportation and Logistics，Taiyuan University of Science and Technology，Taiyuan 030024，China
    2.Shanxi Key Laboratory of Advanced Control and Equipment Intelligence，Taiyuan University of Science and Technology，Taiyuan 030024，China
    3.School of Electric Power and Architecture，Shanxi University，Taiyuan 030024，China
  • Received:2022-04-21 Online:2024-02-01 Published:2024-03-29
  • Contact: Gang XIE E-mail:2013007@tyust.edu.cn;xiegang@tyust.edu.cn

RICH HTML

 1   

PDF (PC)

188

Abstract:

To obtain the dynamic response characteristics of long-span continuous beam bridges under coherent excitation of the bridge deck， a comprehensive analysis was conducted based on the principle of virtual work. Firstly， a dynamic model of a five-axle heavy-load vehicle was established. Then， the bridge's dynamic equation was derived using the modal superposition method， a wheel-deck coherent excitation model was established by considering the geometric and mechanical coupling between the wheels and the bridge. The coupled vibration analysis system of the long-span continuous beam bridge was implemented using Matlab software. Subsequently， the impact of different levels of coherent deck excitation models on the dynamic response of the bridge was investigated. The findings revealed that when the influence of bridge deck irregularity was ignored， the impact coefficients of the bridges were smaller than the standard values. However， as the condition of the bridge deck deteriorated， the dynamic response of the representative cross-section of the structure increased significantly. Moreover， it was observed that the completely coherent excitation model had a greater influence on the dynamic response of the bridges compared to the partially coherent excitation model， exceeding the standard values. The maximum deviation of the deflection amplitude was approximately 7.7%， with a maximum deviation of bending moment amplitude of around 20%. The relative errors in deflection impact coefficient ranged from 4% to 34%， while the relative errors in bending moment impact coefficient ranged from 2% to 43%. Additionally， it was noted that the impact coefficient of the bridge initially increased and then decreased with an increase in vehicle speed. Finally， an envelope diagram illustrating the deflection and moment impact coefficients of the long-span continuous beam bridge was provided. These research findings offer valuable insights for the analysis and study of the structural dynamics and response of continuous beam bridges.

Key words: bridge engineering, bridge deck coherent excitation model, vehicle-bridge coupling, dynamic response, impact coefficient

CLC Number: 

  • U442.5

Fig.1

Schematic of vehicle dynamics model"

Fig.2

Wheel-bridge geometric coupling relationship"

Fig.3

Wheel-bridge mechanics coupling relationship"

Fig.4

Curve of the single-track excitation spatial domain model"

Fig. 5

Coherent excitation spatial domain model sample（Class A）"

Fig.6

Dynamic response of bridge deflection under different bridge deck roughness irregularities （v=80 km/h）"

Fig.7

Dynamic response curve of bridge bending moment under different grades of bridge deck （v=80 km/h）"

Fig.8

Schematic diagram of typical measuring point arrangement of bridge"

Fig.9

Bridge deflection and moment envelopes and relative errors"

1 陆兆文, 夏修身, 史军, 等. 设置负刚度装置的大跨长联连续梁桥地震反应分析[J]. 世界地震工程, 2022, 38(2): 181-187.
Lu Zhao-wen, Xia Xiu-shen, Shi Jun, et al. Seismic response analysis of long span continuous girder bridge with negative stiffness device[J]. World Earthquake Engineering, 2022, 38(2):181-187.
2 韩智强, 谢刚, 李路遥, 等. 大跨连续梁桥车桥耦合振动响应[J]. 科学技术与工程, 2022, 22(11): 4588-4595.
Han Zhi-qiang, Xie Gang, Li Lu-yao, et al. Vehicle-Bridge coupling vibration response of long-span continuous girder bridge[J]. Science Technology and Engineering, 2022, 22(11): 4588-4595.
3 冀伟, 邵天彦. 多跨连续梁桥顶推施工双导梁的优化分析[J]. 浙江大学学报: 工学版, 2021, 55(7): 1289-1298.
Ji Wei, Shao Tian-yan. Optimization analysis of double launching noses during launching construction of multi-span continuous girder bridge[J]. Journal of Zhejiang University (Engineering Science), 2021, 55(7): 1289-1298.
4 陈水生, 赵辉, 李锦华, 等. 特重车各轮相干桥面激励对斜拉桥随机振动的影响[J]. 振动工程学报, 2022, 35(2): 318-330.
Chen Shui-sheng, Zhao Hui, Li Jin-hua, et al. Influence of coherent bridge deck excitation from different wheels of an extra-heavy truck on random vibration of a cable-stayed bridge[J]. Journal of Vibration Engineering, 2022, 35(2): 318-330.
5 周勇军, 薛宇欣, 李冉冉, 等. 桥梁冲击系数理论研究和应用进展[J]. 中国公路学报, 2021, 34(4): 31-50.
Zhou Yong-jun, Xue Yu-xin, Li Ran-ran, et al. State-of-the-art of theory and applications of bridge dynamic load allowance[J]. China Journal of Highway and Transport, 2021, 34(4): 31-50.
6 张向东, 杜东宁, 柴源, 等. 基于车-桥耦合振动理论的连续梁桥影响因素分析[J]. 中南大学学报: 自然科学版, 2016, 47(8): 2848-2854.
Zhang Xiang-dong, Du Dong-ning, Chai Yuan, et al. Analysis of influences of different factors on continuous rigid frame bridges based on theory of vehicle-bridge system coupling vibration[J]. Journal of Central South University (Science and Technology), 2016, 47(8): 2848-2854.
7 赵辉, 陈水生, 夏钰桓. 考虑桥面不平顺随机激励的车桥耦合方程精细积分解法[J]. 北京交通大学学报, 2020, 44(4): 65-75.
Zhao Hui, Chen Shui-sheng, Xia Yu-heng. Precise integration method for vehicle-bridge coupling equation considering random excitation of bridge surface irregularity[J]. Journal of Beijing Jiaotong University, 2020, 44(4): 65-75.
8 邓露, 段林利, 何维, 等. 中国公路车-桥耦合振动车辆模型研究[J]. 中国公路学报, 2018, 31(7): 92-100.
Deng Lu, Duan Lin-li, He Wei, et al. Study on vehicle model for vehicle-bridge coupling vibration of highway bridges in China[J]. Chinese Journal of Highways, 2018, 31(7): 92-100.
9 . 公路桥涵设计通用规范 [S].
10 韩智强, 谢刚, 李路遥, 等. 大跨连续梁桥车桥耦合振动响应[J]. 科学技术与工程, 2022, 22(11): 4588-4595.
Han Zhi-qiang, Xie Gang, Li Lu-yao,et al.Vehicle-bridge coupling vibration response of long-span continuous girder bridge[J]. Science Technology and Engineering, 2022, 22(11): 4588-4595.
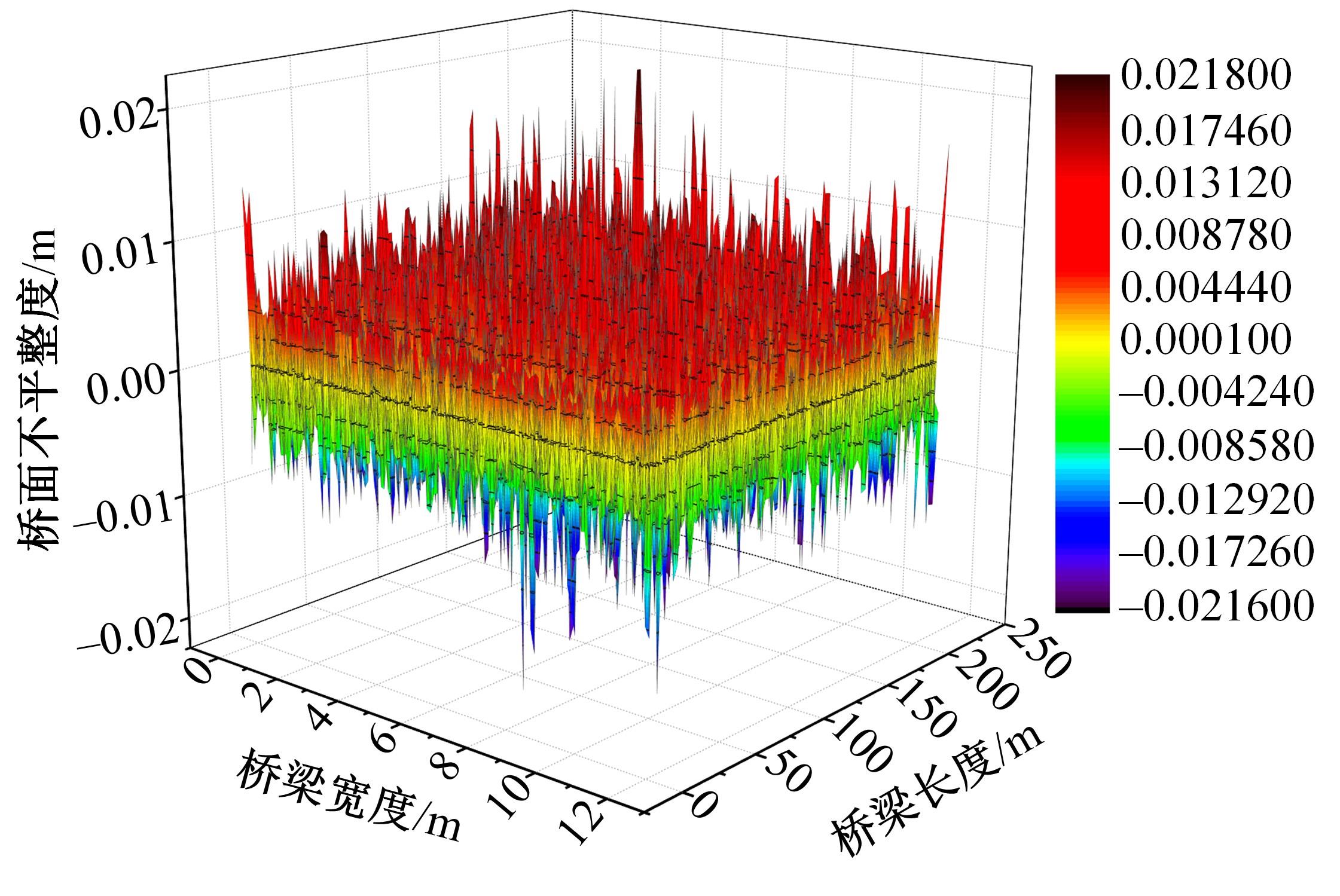
11 桂水荣, 陈水生, 唐志军. 基于Fourier逆变换法的桥面不平度模拟及测试分析[J]. 公路工程, 2007(6): 39-43.
Gui Shui-rong, Chen Shui-sheng, Tang Zhi-jun. Numerical simulation based on Fourier inverse transform and analyse of road surface roughness on bridge[J]. Highway Engineering, 2007(6): 39-43.
12 韩万水, 马麟, 汪炳, 等. 随机车流-桥梁系统耦合振动精细化分析与动态可视化[J]. 中国公路学报, 2013, 26(4): 78-87.
Han Wan-shui, Ma Lin, Wang Bing, et al. Refinement analysis and dynamic visualization of traffic-bridge coupling vibration system[J]. China Journal of Highway and Transport, 2013, 26(4): 78-87.
13 陈水生, 赵辉, 李锦华, 等. 重车各轮相干桥面激励的桥梁随机振动[J]. 长安大学学报: 自然科学版, 2021, 41(4): 43-55.
Chen Shui-sheng, Zhao Hui, Li Jin-hua, et al. Random vibration of bridge excited by bridge deck irregularity of heavy vehicle with coherent wheels[J]. Journal of Changan University (Natural Science Edition), 2021, 41(4): 43-55.
14 韩智强, 谢刚, 周勇军, 等. 曲线桥梁车桥耦合振动数值分析方法[J]. 吉林大学学报: 工学版, 2023, 53(2): 515-522.
Han Zhi-qiang, Xie Gang, Zhou Yong-jun, et al. Numerical analysis method of vehicle-bridge coupling vibration of curved bridge[J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(2): 515-522.
15 Senthilvasan J, Thambiratnam D P, Brameld G H. Dynamic response of a curved bridge under moving truck load[J]. Engineering Structures, 2002, 24: 1283-1293.
16 谭也平, 王健, 刘智超. 基于桥面不平顺导致跳车工况下的车桥相互作用分析[J]. 应用力学学报, 2020, 37(3): 945-952.
Tan Ye-ping, Wang Jian, Liu Zhi-chao. Analysis of vehicle-bridge interaction based on jumping conditions caused by irregular deck[J]. Chinese Journal of Applied Mechanics, 2020, 37(3): 945-952.
17 谭国金, 刘寒冰, 程永春, 等. 基于车-桥耦合振动的简支梁桥冲击效应[J]. 吉林大学学报: 工学版, 2011, 41(1): 62-67.
Tan Guo-jin, Liu Han-bing, Cheng Yong-chun, et al. Analysis of impact of vehicle to simply supported beam bridge based on vehicle-bridge coupled vibration[J]. Journal of Jilin University (Engineering and Technology Edition), 2011, 41(1): 62-67.
18 任宏斌, 陈思忠, 吴志成, 等. 车辆左右车轮路面不平度的时域再现研究[J]. 北京理工大学学报, 2013, 33(3): 257-259.
Ren Hong-bin, Chen Si-zhong, Wu Zhi-cheng, et al. Time domain excitation model of random road profile for left and right wheels[J]. Transactions of Beijing Institute of Technology, 2013, 33(3): 257-259.
19 , 公路桥梁荷载试验规程 [S].
[1] Guo-jun YANG,Ya-hui QI,Xiu-ming SHI. Review of bridge crack detection based on digital image technology [J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(2): 313-332.
[2] Guo-jin TAN,Ji OU,Yong-ming AI,Run-chao YANG. Bridge crack image segmentation method based on improved DeepLabv3+ model [J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(1): 173-179.
[3] Xing WEI,Ya-jie GAO,Zhi-rui KANG,Yu-chen LIU,Jun-ming ZHAO,Lin XIAO. Numerical simulation of residual stress field of stud girth weld in low temperature environment [J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(1): 198-208.
[4] Guan-xu LONG,Xiu-shi ZHANG,Gong-feng XIN,Tao WANG,Gan YANG. Bridge weigh-in-motion combined with machine version [J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(1): 188-197.
[5] Xin-dai ZUO,Jin-quan ZHANG,Shang-chuan ZHAO. Fatigue stiffness degradation and life prediction method of in⁃service concrete T⁃beams [J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(9): 2563-2572.
[6] Ran AN,You-zhi WANG. Shear properties of shear stud connectors under combined tension and shear loading [J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(9): 2554-2562.
[7] Guo-hui CHEN,Ye-yin XU,Ying-hou JIAO. Meshing stiffness calculation and vibration analysis of helical gear considering deflection [J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(7): 1902-1910.
[8] Feng WANG,Shuang-rui LIU,Jia-ying WANG,Jia-ling SONG,Jun WANG,Jiu-peng ZHANG,Xiao-ming HUANG. Size and shape effects of wind drag coefficients for porous structures [J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(6): 1677-1685.
[9] Jun WANG,Jia-wu LI,Feng WANG,Jiu-peng ZHANG,Xiao-ming HUANG. Wind speed distribution in simplified U⁃shaped valley and its effect on buffeting response of long⁃span suspension bridge [J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(6): 1658-1668.
[10] Hua WANG,Long-lin WANG,Zi-mo ZHANG,Xin HE. Safety early warning technology of continuous rigid frame bridges based on crack width variation [J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(6): 1650-1657.
[11] Yu FENG,Jian-ming HAO,Feng WANF,Jiu-peng ZHANG,Xiao-ming HUANG. Analysis of transient wind⁃induced response of long⁃span bridge under nonstationary wind field [J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(6): 1638-1649.
[12] Jian-qing BU,Zhi-bo GUO,Ji-ren ZHANG,Jing-chuan XUN,Xiao-ming HUANG. Finite element analysis method for mechanical properties of steel⁃concrete composite beam bridges with multiple damages [J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(6): 1621-1637.
[13] Qing-xia ZHANG,Ji-lin HOU,Xin-hao AN,Xiao-yang HU,Zhong-dong DUAN. Road roughness identification method based on vehicle impulse response [J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(6): 1765-1772.
[14] Zheng-wei GU,Pan ZHANG,Dong-ye LYU,Chun-li WU,Zhong YANG,Guo-jin TAN,Xiao-ming HUANG. Earthquake⁃induced residual displacement analysis of simply supported beam bridge based on numerical simulation [J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(6): 1711-1718.
[15] Chun-li WU,Shi-ming HUANG,Kui LI,Zheng-wei GU,Xiao-ming HUANG,Bing-tao ZHANG,Run-chao YANG. Analysis of pier action effect under flood based on numerical simulation and statistical analysis [J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(6): 1612-1620.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
Copyright © Journal of Jilin University(Engineering and Technology Edition), All Rights Reserved.
Tel: +86-431-85095297　Fax: +86-431-85094074　E-mail: xbgxb@jlu.edu.cn
Powered by Beijing Magtech Co. Ltd