液压驱动双足机器人运动系统的设计及实现

引用本文

王海燕, 李贻斌, 宁龙霄. 液压驱动双足机器人运动系统的设计及实现. 2014, 44(3): 750-756
WANG Hai-yan, LI Yi-bin, NING Long-xiao. Design and implementation of a hydraulic actuated biped robot motion system. 吉林大学学报(工学版), 2014, 44(3): 750-756 复制到剪切板

Permissions

液压驱动双足机器人运动系统的设计及实现

王海燕, 李贻斌, 宁龙霄

山东大学控制科学与工程学院, 济南 250061

李贻斌(1960),男,教授,博士生导师.研究方向:机器人技术,智能控制理论.E-mail:liyb@sdu.edu.cn

王海燕(1981),女,博士研究生.研究方向:双足机器人,机器人智能控制.

基金:国家自然科学基金重点项目(61233014); 山东大学自主创新基金自主项目(2011JC011);

摘要

提出了一种具有负重能力的8自由度液压驱动双足机器人运动系统。与具有相同负重能力的电驱动双足机器人相比,该机器人体积小、负重能力强、动态性好。由于机器人在空载的情况下,质量主要集中在腿部,提出了一种机器人动态步行时,对质量分布没有限制的机器人侧向平面内保持动态平衡的控制方法,克服了传统倒立摆模型要求忽略机器人腿部质量这一约束,扩大了其适用范围。在多体动力学仿真软件ADAMS环境下对仿真模型进行负重仿真试验和物理样机的空载试验,验证了该液压驱动双足机器人运动系统的有效性。

关键词: 自动控制技术; 负重能力; 液压驱动双足机器人; 动态行走; 多体动力学

中图分类号:TP242.6 文献标志码:A 文章编号:1671-5497(2014)03-0750-07

Design and implementation of a hydraulic actuated biped robot motion system

WANG Hai-yan, LI Yi-bin, NING Long-xiao

School of Control Science and Engineering, Shandong University, Ji'nan 250061, China

Fund:

Abstract

The hydraulic actuated motion system of a biped robot, which has 8 degrees of freedom, with payload capacity is proposed. Comparing with the motor driving robots with the same payload capacity, the robot developed in this research has the advantages of smaller volume and better dynamic characteristics. For that the primary mass is concentrated on the legs when the robot is idle load, a dynamic balance control method in the coronal plane is proposed. Unlike the inverted pendulum model, this control method has no constraint on the mass distribution of the biped robot, which enlarged the application range. The effectiveness of this hydraulic actuated motion system of the biped robot is demonstrated by simulation experiment on Automatic Dynamic Analysis of Mechanical System (ADAMS) and physical prototype idle load experiments.

Keyword: automatic control technology; load ability; hydraulic actuated biped robot; dynamic walk; multibody dynamics

Show Figures

0 引言

机器人领域中的双足动态步行研究,不仅具有重要的学术意义,而且有现实的应用价值^{[ 1]}。目前,双足机器人动态步行控制方法主要包含两部分:基于前馈控制的步行模式离线生成和基于零力矩点(Zero moment point,ZMP)反馈控制的在线调整^{[ 2]},即将双足机器人简化为三维倒立摆模型^{[ 3]},根据指定质心的目标运动,计算所需要的ZMP,通过踝关节力矩来稳定机器人的平衡或姿态^{[ 4, 5]},或者通过改变落脚点来实现机器人稳定步行^{[ 6]}。

目前,与仿人机器人类似,绝大多数具有负重能力的双足机器人都是采用伺服电机配合相应的谐波减速齿轮输出所需的关节驱动力矩^{[ 7]}。通常,具有负重能力的双足机器人每条腿设有6个主动自由度,髋关节和踝关节采用多自由度的正交关节设计。如日本丰田公司推出的“i-foot”^{[ 8]};韩国科学技术院研制的“HUBO Fx-1”^{[ 9]};我国上海交通大学研制的“载人双足步行椅”^{[ 10]};日本千叶工业大学的双足步行机器人“Core”等。鉴于液压驱动器具有功率/质量比大、动态性好、结构紧凑等优点,波士顿动力公司率先研制出高性能的液压驱动仿生机器人,先后推出了液压驱动四足机器人“BigDog”^{[ 11]}和液压驱动双足仿生机器人“Petman”^{[ 12]}。两者均表现出很好的动态性能,有力地促进了液压驱动机器人的发展。

本文提出了一种采用线性伺服液压缸驱动的具有负重能力的双足机器人运功系统。根据液压驱动双足机器人的运动特性,对机器人腿部自由度设置进行了简化,提出了8自由度(每条腿4个主动自由度)的液压驱动双足机器人运动系统。与相同负重能力的电驱动双足机器人相比,该机器人体积、质量均比较小,负重能力强,动态性好。本文提出的双足机器人运动系统空载时,机器人质量主要集中在腿部,克服了传统倒立摆模型要求机器人腿的质量相对于本体可以忽略这一约束,扩大了其适用范围。

1 结构设计

1.1 机械结构部分

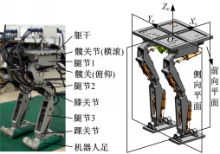
液压驱动双足机器人运动系统的机械结构部分由机器人本体和液压驱动系统构成。目前几乎所有的仿人机器人腿部都选择了6个自由度的构形方式,其分配方式为髋关节3个自由度,膝关节1个自由度,踝关节2个自由度。为了实现稳定行走,避免奇异点,控制机器人的重心高度,6自由度下肢构形的仿人机器人普遍采用屈膝前进方式^{[ 13]}。本文提出的液压驱动双足机器人运动系统也采用屈膝前进的方式,根据液压驱动双足机器人的运动特性,本文对机器人腿部结构进行了简化,提出了每条腿4个主动自由度的液压驱动双足机器人运动系统,如图1所示,机器人躯干用于安装控制器及负重,没有设置自由度。详细参数如表1所示。

	Figure Option View Download New Window
	图1 液压驱动双足机器人样机Fig.1 Prototype of the hydraulic actuated biped robot

表1 液压驱动双足机器人规格 Table 1 Specifications of the hydraulic actuated biped robot

1.1.1 髋关节自由度设置

机器人髋关节若设置旋转自由度,结构参见文献^{[ 14]},则其旋转自由度的驱动器可采用液压伺服马达或者摆动油缸。此时,机器人的负重能力不仅受限于线性液压伺服油缸所能提供的最大输出力,同时还需要考虑在机器人倾倒时,支撑腿上的液压马达/摆动油缸的输出轴所能承受的最大剪切力。而本文提出的液压驱动双足机器人运动系统可以前进、后退和侧向运动,两腿的差速运动可使机器人按照一定的转弯半径转弯。因此机器人髋关节没有设置旋转自由度,而仅设置了横滚和俯仰2个主动自由度。这种构形方式降低了设计制造成本,减轻了机器人本体重量,一定程度地增加了机器人的负重能力。

1.1.2 踝关节自由度设置

双足机器人有静态步行和动态步行两种步行方式。在静态步行中,机器人的质心在地面上的投影始终不能超越支撑多边形的范围;而在动态步行中,质心的投影在某些时刻可以越离支撑多边形。在ADAMS仿真环境下,液压驱动双足机器人负重165 kg静态步行时,单步迈步周期为1 s;质心侧向最大偏移量:左侧140 mm,右侧166 mm(机器人左、右腿腿节1结构不同,静态步行时,侧向偏移量差别比较大);此时,左脚踝关节横滚角的变化范围为[-0.0283,0.0882]rad;而左脚踝关节力矩峰值可达180 N·m,如图2所示。动态步行时,单步迈步周期0.4 s;质心侧向最大偏移量;左侧15 mm,右侧15.5 mm;此时,左脚踝关节横滚角的变化范围为[-0.0012,0.0422] rad;左脚踝关节力矩峰值可达187.92 N·m。由于液压驱动双足机器人动态步行时,机器人踝关节横滚角的变化范围较小,而维持机器人侧向稳定所需的力矩却很大,若踝关节横滚自由度设置为主动所需成本很高;设置为被动不能满足要求。而且,机器人踝关节的横滚角可以通过足底缓冲装置的弹性变形或者躯干的横滚运动进行补偿。因此,从经济性和实用性两方面考虑,本文提出的液压驱动双足机器人运动系统踝关节只设置了俯仰自由度,没有设置横滚自由度。

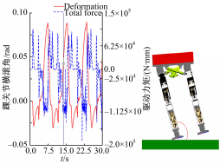	Figure Option View Download New Window
	图2 踝关节横滚角与驱动力矩关系示意图Fig.2 Sketch map for the relationship between the roll angle and the driving torque of the ankle joint

由于在ADAMS环境中创建足底缓冲装置的过程比较复杂,因此,在仿真模型中踝关节横滚自由度没有完全锁死,而是添加了弹性模量为10⁶ (N·mm)/rad的扭矩弹簧和阻尼系数为10⁶ (N·mm·s)/rad的旋转阻尼器。以踝关节横滚角代替足底缓冲装置的弹性变形量。

1.1.3 液压驱动系统

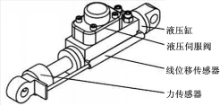
双足机器人运动系统的液压驱动系统包括室内固定液压站、液压油管、阀板、一体化线性液压伺服油缸。其中,一体化线性液压伺服油缸主要由液压缸、液压伺服阀、线位移传感器和力传感器4部分组成,如图3所示。

	Figure Option View Download New Window
	图3 一体化线性液压伺服油缸示意图Fig.3 Sketch map for the linear hydraulic servo cylinder

1.1.4 机器人运动范围

增加驱动髋关节横滚运动的液压缸行程,需要增加机器人的宽度,或者增加第一腿节的长度。综合考虑到油缸的互换性和经济性及机器人结构的美观、实用,液压缸行程的设计值为180~240 mm。

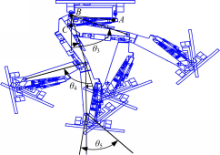
如图4所示,当驱动腿节2俯仰运动的液压缸与腿节1连接轴A的位置确定时,机器人髋关节俯仰运动的转动轴B与驱动腿节2俯仰运动的活塞杆连接轴C之间的距离越小,液压缸有效行程范围内推动机器人髋关节俯仰运动的范围越大,即髋关节俯仰角θ₃的取值范围越大,B与C之间的距离越小,驱动腿节2俯仰运动的液压缸与驱动腿节3俯仰运动的液压缸越容易发生干涉。在避免干涉的情况下,机器人髋关节俯仰角θ₃的取值范围为13.7091°~67.4158°,同理可得,膝关节俯仰角θ₄和踝关节俯仰角θ₅的取值范围分别为-12.8061°~-84.8861°和-8.7925°~42.369°。

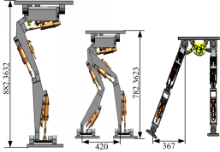
	Figure Option View Download New Window
	图4 双足机器人各腿节运动范围示意图Fig.4 Sketch map for joints range of motion

当机器人各关节俯仰角的范围已确定时,增加机器人腿节2和3的长度,机器人的运动范围随之增加。但是,由于机器人静止站立时其质心不能超过机器人足支撑的多边形,因此,增加机器人腿节2和3的长度,机器人的最大站立高度显著增加;机器人的长度增加量较小,即机器人的运动范围(理论运动空间)与机器人最大站立高度相对应。机器人所能达到的实际运动范围取决于环境和机器人的控制策略。机器人下蹲距离增加,机器人摆动腿向前迈步能力增强,向后迈步能力减弱。本文提出的液压驱动双足机器人运动系统由最大站立高度下蹲100 mm时,向前迈步能力与向后迈步能力相当,前向最大迈步距离约为420 mm,侧向最大迈步距离为367 mm,如图5所示。

	Figure Option View Download New Window
	图5 液压驱动双足机器人运动范围示意图Fig.5 Sketch map for the range of motion of the biped robot

1.2 控制系统部分

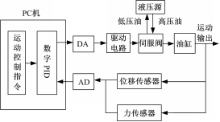
机器人控制系统由研华PCI-1713、PCI-1724U、驱动电路、检测电路等构成,如图6所示。关节运动采用线位移传感器间接测量,并在各关节设有力传感器,以便实现柔顺控制。

	Figure Option View Download New Window
	图6 液压伺服控制系统的基本结构Fig.6 Basic structure of the hydraulic servo control system

2 机器人动态步行控制方法

机器人对地运动方向与支撑足相对于地面的运动方向相反,机器人步态规划的实质是生成机器人双足相对于骨盆中心的运动轨迹^{[ 15]}。本文以机器人躯干上表面几何中心O _c为基坐标原点,建立躯干固定坐标系如图1所示。Z _c与躯干垂直,X _c指向机器人前进方向,机器人前向平面为Z _cO _cX _c平面,侧向平面为Z _cO _cY _c平面。

倒立摆模型和ZMP稳定判据相结合,在双足机器人动态步行控制领域得到了广泛应用。倒立摆的直立摆动过程与机器人的步行过程相对应,即将双足机器人的腿与倒立摆的杆相对应,将双足机器人踝关节的力矩驱动看作是倒立摆的基地关节驱动^{[ 16]}。鉴于倒立摆的特性,该模型只适用于腿部质量和惯量都比较小的情况。本文提出了一种适用范围广,易调节的机器人动态步行侧向平面内保持动态平衡的控制方法(在运动过程中躯干质心加速度时刻在发生变化,故该种方法称为动态平衡法)。包括:①对机器人各部分质量没有限制的双足机器人动步态生成方法;②通过实时检测机器人躯干横滚角,计算摆动腿实际抬高高度,调节机器人质心侧向平面的最大移动距离(间接调整机器人质心侧向平面运动的位移和加速度),保持机器人侧向平面动态平衡的调节机制。

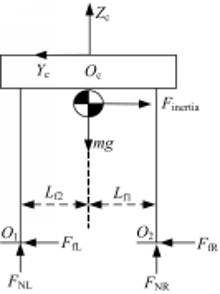
当机器人支撑腿相对于躯干向左加速运动时,如果地面可以提供足够大的摩擦力,则机器人质心相对于地面向右加速运动,如图7所示(图中, F_NL、 F_NR分别为机器人左足、右足受到的正压力; F_fL、 F_fR分别为机器人左足、右足受到的摩擦力)。如果加速度适当,机器人左足作用在地面上的正压力减小为零。此时,左腿离地,机器人不会侧向倾倒。同理,当支撑腿相对于机器人躯干向右加速度运动时,质心相对于地面向左运动。若保持机器人侧向平面的动态平衡,需满足下列两个基本条件: ①适当的初始加速度,保证机器人足可以顺利抬起;如果侧向加速度过大,则机器人会向支撑腿一侧倾倒;如果侧向加速度过小,则机器人则会向摆动腿一侧倾倒;②在运动过程中,侧向平面内由惯性力产生的侧倾力矩和由重力产生的回复力矩相对于平衡点O₁(即ZMP点,质心向右运动平衡点为O₁,质心向左运动平衡点为O₂)的合力矩为零。

	Figure Option View Download New Window
	图7 机器人侧向平面受力示意图Fig.7 Sketch map for the mechanics analysis in the lateral plane

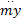
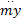
机器人运动过程中,没有人为设置双足支撑阶段,两个迈步周期视为一个运动周期。第1个迈步周期,支撑腿相对于躯干向左加速运动,则mg(- L _f₁-y)+ z _c=0(1)在第2个迈步周期,支撑腿相对于躯干向右加速运动,则mg( L _f ₂-y) + z _c=0(2)式中:m为机器人整体质量;g为重力加速度;y为质心相对于地面沿Y _c方向的位移(与踝关节相对于躯干固定坐标系沿Y _c方向的位移方向相反); 为沿Y _c方向的加速度;z _c为机器人质心到地面的距离;L _f₁为O₁点距离躯干上表面几何中心O _c沿Y _c方向的距离(即质心沿Y _c负方向的最大移动量);L _f₂为O₂点距离躯干上表面几何中心O _c沿Y _c方向的距离(即质心沿Y _c正方向的最大移动量)。

如果机器人左右对称,则L _f₁=L _f₂=L _f。L _f的取值决定了机器人上ZMP点在Y _c方向的理论位置。机器人质心的位置z _c可以通过试验获得,本文用躯干上表面几何中心到地面的距离z代替。z _c与z的差别可以通过L _f调节弥补。

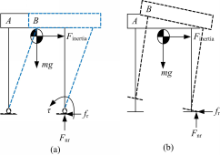
对于踝关节横滚自由度为主动的双足机器人,理想状态下,躯干在侧向平面内水平运动,即躯干横滚角为零(如图8(a)所示);而对于踝关节没有横滚自由度的双足机器人(如图8(b)所示),躯干横滚运动不可避免。因此,机器人摆动腿实际抬高高度H _n应大于期望值H _e。在踏步阶段,采用本文提出的动态平衡的控制方法,不需要计算平衡点O₁或者O₂是否在支撑足构成的凸多边形内,只需要根据机器人摆动腿的实际抬高高度H _n与期望的抬高高度H _e的差值调节L _f值,保持机器人侧向平面的稳定。调节L _f,使得H _n大于H _e,但尽可能接近kH _e。其中,k>1,k与机器人的结构有关,与负重及机器人的运动特性无关。

	Figure Option View Download New Window
	图8 机器人侧向平面躯干位姿示意图Fig.8 Sketch map for the trunk position and posture in the lateral plane

本文提出的机器人侧向平面内保持动态平衡的控制方法适用的周期范围为0.3~0.5 s(与成年人正常的迈步周期相同),如果机器人的周期大于0.5 s,保证机器人侧向平面稳定运动,需要提供的质心初始加速度较大,L _f值增加,保持机器人侧向平面稳定的L _f取值范围较小,不易调节。

3 试验验证

机器人运动时,Y _c方向采用本文提出的保持机器人质心侧向平面内动态平衡的控制方法。当机器人前进、后退时,X _c、Z _c方向步态生成方法与山东大学机器人研究中心研制的“Scalf”^{[ 17]}系列液压驱动四足机器人步态生成方法相同,即分别根据机器人X _c、Z _c方向步长、速度信息,采用三次多项式插值方法,生成相应摆动腿踝关节运动轨迹;支撑腿X _c方向相对于躯干坐标系匀速直线运动,Z _c方向抬高高度为零。机器人向右转弯时,左腿踝关节X _c方向步长大于右腿踝关节X _c方向步长。同理,向左转弯时,右腿踝关节X _c方向步长大于左腿踝关节X _c方向步长。

3.1 负重仿真

机器人模型在ADAMS仿真环境下进行负重仿真试验。令机器人负重160 kg(机器人物理样机负重能力受限于液压动力源输出液压油的最大油压及液压缸活塞杆的强度。ADAMS仿真模型不受此限制。本文提出的液压驱动双足机器人运动系统,物理样机试验时采用的负载重量最大为80 kg,但理论计算允许的最大负重约200 kg,因此,本文在ADAMS仿真环境下,令机器人负重160 kg)。

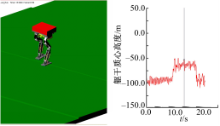
Y _c方向采用本文提出的保持机器人质心侧向平面内“动态平衡”的控制方法,X _c方向采用传统的阻抗控制,机器人表现出良好的运动特性。较小的地面起伏(20 mm台阶)对机器人的运动不产生影响,如图9所示,机器人周期0.4 s,上台阶后机器人正常向前运动,下台阶后机器人仍然正常继续向前运动。当机器人前向运动时,机器人步长400 mm(达到了设计步长),周期0.3 s时,前进速度可达1.32 m/s,如图10所示。

	Figure Option View Download New Window
	图9 机器人负重上下台阶运动仿真Fig.9 Simulation result for climbing stairs with load

	Figure Option View Download New Window
	图10 机器人负重前向运动仿真Fig.10 Simulation result for walking along with load

由于机器人没有设置旋转自由度,机器人转弯通过双腿X _c方向差速运动来实现。当迈步周期为0.4 s,双腿速度差40 mm时,机器人转弯半径大约是其宽度的1.5倍,如图11所示。

	Figure Option View Download New Window
	图11 机器人负重圆周运动仿真Fig.11 The simulation result for walking in a circle with load

3.2 空载物理样机试验

液压驱动双足机器人运动系统的机械本体部分(包括关节驱动伺服液压缸)总质量约40 kg,机器人单腿的质量约为14 kg。显然,在不负重的情况下,本文提出的液压驱动双足机器人运动系统不符合倒立摆模型前提假设。但是,按照本文提出的机器人侧向平面内保持“动态平衡”的控制方法,X _c、Z _c方向仅采用位置控制,液压驱动双足机器人运动系统即可完成前进(见图12)、后退(见图13)、转弯等功能性动作。

	Figure Option View Download New Window
	图12 试验视频截图——机器人前进Fig.12 Video Snapshots Genius(walk along)

	Figure Option View Download New Window
	图13 试验视频截图——机器人后退Fig.13 Video Snapshots Genius(walk back)

4 结束语

设计制造了具有负重能力的液压驱动双足机器人运动系统,其动态步行周期范围为0.3~0.5 s。在ADAMS仿真环境下,该机器人运动系统动态行走,前向运动最大步幅达400 mm(达到了机器人的最大设计步长),最大行走速度1.32 m/s。本文提出的机器人侧向平面内保持动态平衡的控制方法适用范围广、易调节。仿真试验和物理样机试验验证了其正确性和有效性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	管贻生. 仿人机器人[M]. 北京: 清华大学出版社, 2007: 97-157. [本文引用:1]
[2]	Kim J H. Walking pattern generation of a biped walking robot using convolution sum[C]∥The 7th IEEE-RAS International Conference on Humanoid Robots, Pittsburgh, PA, USA, 2007: 539-544. [本文引用:1]
[3]	Kajita S, Matsumoto O, Saigo M. Real-time 3D walking pattern generation for a biped robot with telescopic legs[C]∥Proceedings of the 2001 IEEE International Conference on Robotics and Automation, Seoul, Korea, 2001: 2299-2306. [本文引用:1]
[4]	Kim J H, Oh J H. Walking control of the humanoid platform KHR-1 based on torque feedback control[C]∥Proceedings of the 2004 IEEE International Conference on Robotics and Automation, New Orleans, LA, USA, 2004: 623-628. [本文引用:1]
[5]	Kim J Y, Park I W, Oh J H. Realization of dynamic stair climbing for biped humanoid robot using force/torque sensors[J]. Journal of Intelligent and Robotic Systems, 2009, 56(4): 389-423. [本文引用:1] [JCR: 0.827]
[6]	Raibert M H. Legged Robots that Balance[M]. Cambridge, MA: MIT press, 1986: 29-55. [本文引用:1]
[7]	陈恳, 付成龙. 仿人机器人理论与技术[M]. 北京: 清华大学出版社, 2010: 1-17. [本文引用:1]
[8]	Toyota motor corporation[EB/OL]. [2013-01-26]. Toyota motor corporation[EB/OL]. [2013-01-26]. http://www.toyota-global.com/innovation/partner_robot/aichi_expo_2005/index03.html. [本文引用:1]
[9]	Kim J H, Kim J Y, Oh J H. Adaptive walking pattern generation and balance control of the passenger-carrying biped robot, HUBO FX-1, for variable passenger weights[J]. Autonomous Robots, 2011, 30(4): 427-443. [本文引用:1] [JCR: 1.908]
[10]	唐矫燕. 载人两足步行椅机器人稳定性分析与控制策略[D]. 上海: 上海交通大学机械工程与动力学院, 2011. Tang Jiao-yan. Human in the loop gait stability analysis and control strategy of biped walking-chair robot[D]. Shanghai: School of Mechanical and Dynamical Engineering, Shanghai Jiao Tong University, 2011. [本文引用:1]
[11]	Boston Dynamics[EB/OL]http://www.bostondynamics.com/robot_bigdog.html. [本文引用:1]
[12]	Boston Dynamics[EB/OL]http://www.bostondynamics.com/robot_petman.html. [本文引用:1]
[13]	张倡, 黄强, 李光日, 等. 具有7自由度和双球型髋关节蛳人机器人下肢运动分析与规划[J]. 机器人, 2007, 29(6): 558-562. Zhang Chang, Huang Qiang, Li Guang-ri, et al. Kinematics analysis and motion planning of a humanoid leg with 7DOF and double spherical hip joint[J]. Robotica, 2007, 29(6): 558-562. [本文引用:1] [JCR: 0.88]
[14]	李贻斌, 王海燕, 马昕, 等. 具有负重能力的液压驱动双足机器人下肢机构[P]. 中国: 2012100217832, 2013-08-07. [本文引用:1]
[15]	Kim J Y, Park I W, Oh J H. Walking control algorithm of biped humanoid robot on uneven and inclined floor[J]. Journal of Intelligent and Robotic Systems, 2007, 48(4): 457-484. [本文引用:1] [JCR: 0.827]
[16]	胡凌云, 孙增圻. 双足机器人步态控制研究方法综述[J]. 计算机研究与发展, 2005, 42(5): 728-733. Hu Ling-yun, Sun Zeng-qi. Survey on gait control strategies for biped robot[J]. Journal of Computer Research and Development, 2005, 42(5): 728-733. [本文引用:1]
[17]	Rong Xue-wen, Li Yi-bin, Ruan Jiu-hong, et al. Design and simulation for a hydraulic actuated quadruped robot[J]. Journal of Mechanical Science and Technology, 2012, 26(4): 1171-1177. [本文引用:1] [JCR: 0.616]

2007

0.0

... 0 引言机器人领域中的双足动态步行研究,不仅具有重要的学术意义,而且有现实的应用价值^[1] ...

2007

0.0

... 目前,双足机器人动态步行控制方法主要包含两部分:基于前馈控制的步行模式离线生成和基于零力矩点(Zero moment point,ZMP)反馈控制的在线调整^[2],即将双足机器人简化为三维倒立摆模型^[3],根据指定质心的目标运动,计算所需要的ZMP,通过踝关节力矩来稳定机器人的平衡或姿态^[4,5],或者通过改变落脚点来实现机器人稳定步行^[6] ...

2001

0.0

2004

0.0

2009

0.827

0.0

. 2009, 56(4):389-423 DOI:10.1007/s10846-009-9324-z

Realization of dynamic stair climbing for biped humanoid robot using force/torque sensors

1.Seoul National University of Technology Humanoid Robot Research Laboratory, School of Mechanical Design and Automation Engineering 138 Gongrung-gil, Nowon-gu Seoul 139-743 South Korea 2.Kwangwoon University Department of Information and Control Engineering 447-1, Wolgye-dong, Nowon-gu Seoul 139-70 South Korea 3.Korea Advanced Institute of Science and Technology HUBO Laboratory, Humanoid Robot Research Center, Department of Mechanical Engineering 373-1 Guseong-dong Yuseong-gu Daejeon 305-701 South Korea

This paper proposes a control algorithm for the dynamic stair climbing of a human-sized biped humanoid robot. Dynamic stair climbing can cause more instability than dynamic biped walking on the ground because stair climbing requires an additional vertical motions and a large step length. We assume that stair configuration is already known and only use force/torque sensors at ankle joint to achieve a control algorithm for a stable dynamic stair climbing. We describe a stair climbing pattern generation and stair climbing stages, and then propose a real-time balance control algorithm which is composed of several online controllers. Each online controller is addressed in detail with experimental results. Finally, the effectiveness and performance of the proposed control algorithm are verified through a dynamic stair climbing experiment of KHR-2.

1986

0.0

2010

0.0

... 目前,与仿人机器人类似,绝大多数具有负重能力的双足机器人都是采用伺服电机配合相应的谐波减速齿轮输出所需的关节驱动力矩^[7] ...

2013

0.0

... ^[8] ...

2011

1.908

0.0

. 2011, 30(4):427-443 DOI:10.1007/s10514-011-9227-2

Adaptive walking pattern generation and balance control of the passenger-carrying biped robot, HUBO FX-1, for variable passenger weights

1.Construction Robot and Automation Laboratory, Department of Civil and Environmental Engineering, Yonsei University, 134, Shinchon-dong, Seodaemun-gu, Seoul, 120-749 South Korea 2.Humanoid Robot Research Laboratory, School of Mechanical Design & Automation Engineering, Seoul National University of Science and Technology, Gongrung-Dong, Nowon-Gu, Seoul, 139-743 South Korea 3.HUBO Laboratory, Humanoid Robot Research Center, Department of Mechanical Engineering, Korea Advanced Institute of Science and Technology, 373-1, Guseong-dong, Yuseong-gu, Daejeon, 305-701 South Korea

A passenger-carrying biped robot is a practical robot capable of carrying a passenger for both entertainment purposes and disabled transport by means of biped walking. In the walking controls of the biped walking robot, changes in the payload are not generally considered. However, in the case of a passenger-carrying biped robot, the range of possible payloads for passenger weight is relatively wide, from zero to approximately one hundred kgf. In the authors’ previous research pertaining to passenger-carrying biped robots, the robot was modeled using a specific passenger weight; hence, the control parameters were tuned for it and kept to be constant. However, the previous method’s weakness was a decrease in the walking performance and walking stability of the robot when the passenger’s weight was much heavier or lighter than the predefined passenger weight. Therefore, in this paper, the walking pattern generation and balance control methods are developed to adaptively cope with variable passenger weights. These methods are then experimentally verified to ensure that the walking performance could be preserved uniformly for a variation of passenger weights.

... ^[9] ...

2011

0.0

... ^[10] ...

0.0

... ^[11]和液压驱动双足仿生机器人#cod#x0201c ...

0.0

... ^[12] ...

2007

0.88

0.0

. 2007, 29(6):558-562

Kinematics analysis and motion planning of a humanoid leg with 7DOF and double spherical hip joint

提出了具有7自由度和双球型髋关节的仿人机器人下肢机构.它和传统的6自由度双足步行机构相比,具有下述两大优点.首先双球型髋关节使机器人在不增加腰部关节的情况下实现腰部的基本运动功能,使机器人能够直立行走;其次在给定腰和足部位置时,它也能和人类一样实现转动双腿的动作.本文还对该复杂机构进行了运动特性分析、运动学求解、运动规划和实验验证.

... 为了实现稳定行走,避免奇异点,控制机器人的重心高度,6自由度下肢构形的仿人机器人普遍采用屈膝前进方式^[13] ...

0.0

... 机器人髋关节若设置旋转自由度,结构参见文献^[14],则其旋转自由度的驱动器可采用液压伺服马达或者摆动油缸 ...

2007

0.827

0.0

. 2007, 48(4):457-484 DOI:10.1007/s10846-006-9107-8

Walking control algorithm of biped humanoid robot on uneven and inclined floor

1.Korea Advanced Institute of Science and Technology HUBO Laboratory, Humanoid Robot Research Center, Department of Mechanical Engineering 373-1 Guseong-dong Yuseong-gu Daejeon 305-701 South Korea 373-1 Guseong-dong Yuseong-gu Daejeon 305-701 South Korea

This paper describes walking control algorithm for the stable walking of a biped humanoid robot on an uneven and inclined floor. Many walking control techniques have been developed based on the assumption that the walking surface is perfectly flat with no inclination. Accordingly, most biped humanoid robots have performed dynamic walking on well designed flat floors. In reality, however, a typical room floor that appears to be flat has local and global inclinations of about 2°. It is important to note that even slight unevenness of a floor can cause serious instability in biped walking robots. In this paper, the authors propose an online control algorithm that considers local and global inclinations of the floor by which a biped humanoid robot can adapt to the floor conditions. For walking motions, a suitable walking pattern was designed first. Online controllers were then developed and activated in suitable periods during a walking cycle. The walking control algorithm was successfully tested and proved through walking experiments on an uneven and inclined floor using KHR-2 (KAIST Humanoid robot-2), a test robot platform of our biped humanoid robot, HUBO.

... 2 机器人动态步行控制方法机器人对地运动方向与支撑足相对于地面的运动方向相反,机器人步态规划的实质是生成机器人双足相对于骨盆中心的运动轨迹^[15] ...

2005

0.0

. 2005, 42(5):728-733

Survey on gait control strategies for biped robot

概括地介绍了双足机器人步态控制领域内的主要研究思路.详细阐述了基于双足动力学特征的3种建模方法,包括倒立摆模型、被动步态模型、质量弹簧模型的特点.另外讨论了两种常用的约束条件(稳定判据与能量约束)和3种智能控制方法(神经元理论、模糊逻辑与遗传算法)在双足机器人步态控制中的研究情况.

... 倒立摆的直立摆动过程与机器人的步行过程相对应,即将双足机器人的腿与倒立摆的杆相对应,将双足机器人踝关节的力矩驱动看作是倒立摆的基地关节驱动^[16] ...

2012

0.616

0.0

. 2012, 26(4):1171-1177 DOI:10.1007/s12206-012-0219-8

Design and simulation for a hydraulic actuated quadruped robot

<li>1.School of Control Science and Engineering, Shandong University, Jinan, 250061, China</li><li>2.Advanced Vehicle and Robot Institute, Shandong Jiaotong University, Jinan, 250031, China</li>

Abstract
This paper describes the mechanical configuration of a quadruped robot firstly. Each of the four legs consists of three rotary joints. All joints of the robot are actuated by linear hydraulic servo cylinders. Then it deduces the forward and inverse kinematic equations for four legs with D-H transformation matrices. Furthermore, it gives a composite foot trajectory composed of cubic curve and straight line, which greatly reduces the velocity and acceleration fluctuations of the torso along forward and vertical directions. Finally, dynamics cosimulation is given with MSC.ADAMS and MATLAB. The results of co-simulation provide important guidance to mechanism design and parameters preference for the linear hydraulic servo cylinders.

... ^[17]系列液压驱动四足机器人步态生成方法相同,即分别根据机器人X_c、Z_c方向步长、速度信息,采用三次多项式插值方法,生成相应摆动腿踝关节运动轨迹 ...