采用强跟踪中心差分滤波器的汽车状态和参数估计

引用本文

李静, 张家旭, 张艳华, 陈立军. 采用强跟踪中心差分滤波器的汽车状态和参数估计. 吉林大学学报（工学版）, 2017, 47(5): 1329-1335
LI Jing, ZHANG Jia-xu, ZHANG Yan-hua, CHEN Li-jun. Estimation of vehicle state and parameter based on strong tracking CDKF. Journal of Jilin University Engineering and Technology Edition, 2017, 47(5): 1329-1335 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201705001
Permissions

采用强跟踪中心差分滤波器的汽车状态和参数估计

李静¹, 张家旭^1,², 张艳华¹, 陈立军³

1.吉林大学汽车仿真与控制国家重点实验室,长春 130022

2.中国第一汽车集团公司技术中心,长春 130011

3.吉林大学大数据和网络管理中心,长春 130022

通信作者:陈立军(1960-),男,副研究员.研究方向:计算机应用.E-mail:clj@jlu.edu.cn

作者简介:李静(1974-),男,教授,博士生导师.研究方向:汽车地面力分析与控制.E-mail:liye1129@163.com

基金项目:国家自然科学基金项目(51275206)

摘要

采用3自由度非线性汽车动力学模型作为汽车状态和时变参数估计的标称模型,利用强跟踪中心差分卡尔曼滤波器(CDKF)对汽车的纵向速度、质心侧偏角和横摆角速度等信息,以及标称模型的前、后轴等效时变侧偏刚度进行了估计。为验证强跟踪CDKF算法的估计性能,采用模型在环和硬件在环的方式进行多种工况的仿真验证。结果表明,该算法具有可行性和准确性。

关键词: 车辆工程; 汽车动力学; 时变模型参数; 强跟踪中心差分卡尔曼滤波器; 状态和参数估计

中图分类号:U461 文献标志码:A 文章编号:1671-5497(2017)05-1329-07

Estimation of vehicle state and parameter based on strong tracking CDKF

LI Jing¹, ZHANG Jia-xu^1,², ZHANG Yan-hua¹, CHEN Li-jun³

1.State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022, China

2.Research and Development Center, China FAW Group Corporation, Changchun 130011, China

3.Big Data and Network Management Center, Jilin University, Changchun 130022,China

Abstract

A 3-DOF nonlinear dynamic model of vehicle is established as nominal model of vehicle state and parameter estimation. Strong tracking Central Difference Kalman Filter (CDKF) is adopted to simultaneously estimate the longitudinal velocity, side slip angle and yaw rate of the vehicle and the equivalent lateral stiffness of the axle. In order to verify the performance of the strong tracking CDFK algorithm, typical cases using model-in-the-loop simulation systems are carried out. Simulation results show that the algorithm is effective and can get high accuracy.

Key words: vehicle engineering; vehicle dynamics; time-varying model parameters; strong tracking central difference Kalman filter; states and parameters estimation

Show Figures

0 引言

准确实时获得汽车行驶过程中的状态信息是汽车主动安全控制领域的关键问题之一, 也是实现闭环反馈控制的前提和必要条件^[1]。但由于技术和成本方面的原因, 这些信息通常无法直接测量, 而由此衍生出来的利用车载传感器测量得到的信息来实时估计汽车行驶过程中的纵向速度、质心侧偏角等状态信息成为近年来国内外研究的热点^{[2, 3]}。

目前较为常用的汽车状态估计算法主要有扩展卡尔曼滤波器^{[4, 5]}, 状态观测器估计算法^{[6, 7]}和滚动时域优化估计算法^{[8, 9]}等。文献[10]采用非线性车辆动力学模型作为算法设计的标称模型, 应用无迹卡尔曼滤波器对汽车行驶过程中的纵向速度、侧向速度和横摆角速度等状态以及路面附着系数进行估计。文献[11]基于李雅普诺夫稳定性理论设计非线性观测器估计车辆的纵向速度、侧向速度和路面附着系数, 但该方法未考虑标称模型的不确定性对系统稳定性的影响。文献[12]采用线性二自由度时变参数模型和增益规划调度策略估计车辆的质心侧偏角, 算法运行过程中需要实时获取车辆的纵向速度作为时变参数, 但车辆的纵向速度信息难于测量。车辆在运动过程中的许多参数值是不断变化的, 例如:整车质量、质心位置和轮胎侧偏刚度等, 这些不断变化的参数对基于动力学模型的汽车状态估计算法的性能有重要影响。轮胎与地面的作用力是控制车辆运动的核心因素, 故可将车辆内部参数变化对汽车状态估计的影响折算到前后轴等效的时变侧偏刚度参数产生的影响。为此, 在估计车辆纵向速度、质心侧偏角和横摆角速度等状态信息时, 并行估计车辆标称模型的前后轴等效时变侧偏刚度参数可以提高车辆状态信息的估计精度和系统的鲁棒性。

强跟踪中心差分卡尔曼滤波器(Strong central difference Kalman filter, CDKF)基于强跟踪滤波器理论框架, 采用中心差分变换以二阶泰勒精度逼近非线性高斯系统状态的后验均值和协方差, 无需计算非线性函数的雅克比矩阵, 且兼具强跟踪滤波器鲁棒性强的特点^{[13, 14]}。为此, 本文采用3自由度非线性车辆动力学模型作为车辆状态估计算法设计的标称模型, 利用强跟踪CDKF对车辆的纵向速度、质心侧偏角和横摆角速度等状态信息与车辆标称模型的前后轴等效时变侧偏刚度参数并行估计。最后, 采用模型在环和硬件在环两种方式对强跟踪CDKF算法进行多种工况的仿真验证。结果表明, 该算法可以有效抑制滤波发散, 同时具有良好的估计精度。

1 车辆动力学模型

本文在线性2自由度车辆动力学模型的基础上建立包括纵向运动、侧向运动和横摆运动的3自由度车辆动力学模型, 并将其作为汽车状态和参数估计算法设计的标称模型, 该模型的结构示意图如图1所示。

	Figure Option View Download New Window
	图1 车辆3自由度动力学模型示意图Fig.1 Schematic diagram of 3-DOF vehicle dynamic model

如图1所示, X_eO_eY_e为地面固定坐标系, X_vO_vY_v为车辆固定坐标系。其中, 车辆固定坐标系以车辆重心为原点O_v, 规定汽车的纵向水平轴为X_v轴, 向前为正; 过原点与X_v轴垂直的方向规定为Y_v轴, 向左为正^[15]。该3自由度车辆模型的动力学方程为:

$\overset{\cdot}{r} = \frac{a^{2} k_{1} + b^{2} k_{2}}{I_{z}} \frac{r}{v_{x}} + \frac{a k_{1} - b k_{2}}{I_{z}} β - \frac{a k_{1}}{I_{z}} δ$ （1）

$\overset{\cdot}{β} = \frac{a k_{1} - b k_{2} - m v_{x}^{2}}{m} \frac{r}{v_{x}^{2}} + \frac{k_{1} + k_{2}}{m} \frac{β}{v_{x}} - \frac{k_{1}}{m} \frac{δ}{v_{x}}$ （2）

${\overset{\cdot}{v}}_{x} = a_{x} + v_{y} r = a + β v_{x} r$ （3）

$\begin{matrix} a_{y} = \frac{a k_{1} - b k_{2}}{m v_{x}} r + \frac{k_{1} + k_{2}}{m} β - \frac{k_{1}}{m} δ \end{matrix}$ (4)

式中:a、b为车辆质心到前轴、后轴的距离; k₁、k₂为前后轴等效的侧偏刚度; m为整车质量; I_z为横摆转动惯量; v_x为纵向速度; v_y为侧向速度; r为横摆角速度; β 为质心侧偏角; δ 为前轮转角; a_x为纵向加速度; a_y为侧向加速度。

本文基于车载传感器测量得到的纵向加速度a_x、侧向加速度a_y和前轮转角δ (通过测量得到的方向盘转角间接获取), 实时估计车辆的纵向速度v_x、质心侧偏角β 和横摆角速度r。定义状态变量为:

$\begin{matrix} x_{s} = [v_{x} {βr]}^{T} (5) \end{matrix}$

定义车辆模型的时变参数集为:

$\begin{matrix} ρ = [k_{1} k_{2}]^{T} (6) \end{matrix}$

将系统的状态向量与时变参数并行估计, 从而得到扩展形式的状态向量为:

$\begin{matrix} x = [x_{s} {ρ]}^{T} (7) \end{matrix}$

系统输入为:

$\begin{matrix} u = [a_{x} {δ]}^{T} (8) \end{matrix}$

观测向量为:

$\begin{matrix} z = [a_{y}] (9) \end{matrix}$

考虑式(1)~(4)和式(7)~(9), 利用前向欧拉积分法可得包含时变参数的车辆系统离散化状态方程和观测方程:

$\begin{matrix} \{\begin{matrix} x_{k + 1} = f (x_{k}, u_{k}) + [\begin{matrix} w_{k} \\ η_{k} \end{matrix}] = [\begin{matrix} f_{s} (x_{s, k}, u_{k}) \\ ρ_{k} \end{matrix}] + [\begin{matrix} w_{k} \\ η_{k} \end{matrix}] \\ z_{k + 1} = h (x_{k + 1}, u_{k + 1}) + v_{k + 1} \end{matrix} \end{matrix}$ （10）

式中:w_k、v_k为状态估计的过程噪声和观测噪声, η _k为参数估计噪声, 彼此相互独立, 均为零均值的高斯白噪声, 设它们的协方差矩阵分别为H、R和G, 并且令Q=diag{H G}。

2 强跟踪中心差分卡尔曼滤波器

强跟踪CDKF使用正交性原理, 通过在状态预测协方差矩阵中引入渐消因子的方法, 强迫输出残差具有正交性或近似正交性, 从而对系统的突变状态具有跟踪能力^[16]。同时, 强跟踪CDKF采用中心差分变换逼近非线性高斯系统状态的后验均值和协方差, 不需要计算复杂的雅克比矩阵, 提高了运算效率和滤波精度。算法的具体计算步骤如下:

(1)预测方程

按照对称采样策略, 利用状态向量x在k时刻的统计特性( $\begin{matrix} {\hat{x}}_{k} \end{matrix}$ , P_k)来计算Sigma点ξ _i_,_k及其权系数 $\begin{matrix} W_{i}^{m} \end{matrix}$ 、 $\begin{matrix} W_{i}^{c 1} \end{matrix}$ 和 $\begin{matrix} W_{i}^{c 2} \end{matrix}$ , 即:

$\{\begin{matrix} ξ_{0, k} = {\hat{x}}_{k} \\ ξ_{i, k} = {\hat{x}}_{k} + {(h \sqrt[]{P_{k}})}_{i} \\ ξ_{i + n, k} = {\hat{x}}_{k} - {(h \sqrt[]{P_{k}})}_{i} \end{matrix}$ （11）

$\{\begin{matrix} W_{0}^{m} = \frac{h^{2} - n}{h^{2}} \\ W_{i}^{m} = \frac{1}{2 h^{2}} \\ W_{i}^{c 1} = \frac{1}{4 h^{2}} \\ W_{i}^{c 2} = \frac{h^{2} - 1}{4 h^{2}} \end{matrix}$ （12）

式中:h为中心差分区间长度, 且h²≥ 1; i=1, 2, …, n。

ξ _i_,_k通过非线性状态函数传播为γ _i_,_k+₁_|k, 再由γ _i_,_k+₁_|k计算状态预测 $\begin{matrix} {\hat{x}}_{k + 1 | k} \end{matrix}$ 和协方差矩阵 $\begin{matrix} P_{k + 1 | k}^{(l)} \end{matrix}$ 为:

$γ_{i, k + 1 | k} = f (ξ_{i, k}, u_{k}), i = 0, 1, \dots, 2 n$ (13)

${\hat{x}}_{k + 1 | k} = \overset{2 n}{\sum_{i = 0}} W_{i}^{m} γ_{i, k + 1 | k}$ （14）

$P_{k + 1 | k}^{(l)} = \overset{n}{\sum_{i = 1}} [W_{i}^{c 1} (γ_{i, k + 1 | k} - γ_{i + n, k + 1 | k})^{2} + W_{i}^{c 2} (γ_{i, k + 1 | k} + γ_{i + n, k + 1 | k} - 2 γ_{0, k + 1 | k})^{2}] + Q$ （15）

为了使滤波器具有应对系统模型不确定的鲁棒性, 在状态预测协方差矩阵 $\begin{matrix} P_{k + 1 | k}^{(l)} \end{matrix}$ 中引入渐消因子矩阵λ _k+₁得:

$P_{k + 1 | k} = λ_{k + 1} \overset{n}{\sum_{i = 1}} [W_{i}^{c 1} (γ_{i, k + 1 | k} - γ_{i + n, k + 1 | k})^{2} + W_{i}^{c 2} (γ_{i, k + 1 | k} + γ_{i + n, k + 1 | k} - 2 γ_{0, k + 1 | k})^{2}] + Q$ （16）

渐消因子矩阵λ _k+₁由以下方法确定:

$λ_{k + 1} = \{\begin{matrix} C_{k + 1}, C_{k + 1} > 1 \\ I_{n \times n}, C_{k + 1} \leq 1 \end{matrix}$ （17）

式中：

$C_{k + 1} = tr [N_{k + 1}] / tr [M_{k + 1}]$ （18）

$N_{k + 1} = V_{k + 1} - R - [P_{{\tilde{x}}_{k + 1} {\tilde{z}}_{k + 1}}^{(l)}]^{T} [P_{k + 1 | k}^{(l)}]^{- 1} Q [P_{k + 1 | k}^{(l)}]^{- 1} P_{{\tilde{x}}_{k + 1} {\tilde{z}}_{k + 1}}^{(l)}$ （19）

$M_{k + 1} = [P_{k + 1 | k}^{(l)} - Q] [P_{k + 1 | k}^{(l)}]^{- 1} P_{{\tilde{x}}_{k + 1} {\tilde{z}}_{k + 1}}^{(l)} [P_{{\tilde{x}}_{k + 1} {\tilde{z}}_{k + 1}}^{(l)}]^{T} [P_{k + 1 | k}^{(l)}]^{- 1}$ （20）

tr(· )为求矩阵迹的算子; $\begin{matrix} P_{{\tilde{z}}_{k + 1}}^{(l)} \end{matrix}$ 和 $\begin{matrix} P_{{\tilde{x}}_{k + 1} {\tilde{z}}_{k + 1}}^{(l)} \end{matrix}$ 分别为未引入渐消因子的子协方差矩阵和互协方差矩阵; V_k+₁为实际输出残差序列的协方差矩阵, 由以下方法确定:

$V_{k + 1} = \{\begin{matrix} ε_{1} {ε^{T}}_{1}, k = 0 \\ \frac{σ V_{k} + ε_{k + 1} {ε^{T}}_{k + 1}}{1 + σ}, k \geq 1 \end{matrix}$ （21）

$\begin{matrix} ε_{k + 1} = z_{k + 1} - {\hat{z}}_{k + 1 | k} \end{matrix}$ (22)

式中:0< σ ≤ 1为遗忘因子, 通常取σ =0.95。

利用 $\begin{matrix} {\hat{x}}_{k + 1 | k} \end{matrix}$ 和 $\begin{matrix} P_{k + 1 | k}^{(l)} \end{matrix}$ 确定 $\begin{matrix} P_{_{{\tilde{z}}_{k + 1}}}^{(l)} \end{matrix}$ 和 $\begin{matrix} P_{_{{\tilde{x}}_{k + 1} {\tilde{z}}_{k + 1}}}^{(l)} \end{matrix}$ , 计算方法如下:

$\{\begin{matrix} ξ_{0, k + 1 | k}^{(l)} = {\hat{x}}_{k + 1 | k} \\ ξ_{i, k + 1 | k}^{(l)} = {\hat{x}}_{k + 1 | k} + {(h \sqrt[]{P_{k + 1 | k}^{(l)}})}_{i} \\ ξ_{i + n, k + 1 | k}^{(l)} = {\hat{x}}_{k + 1 | k} - {(h \sqrt[]{P_{k + 1 | k}^{(l)}})}_{i} \end{matrix}$ (23)

$i = 1, 2, \dots, n$

$χ_{_{i, k + 1 | k}}^{(l)} = h (ξ_{i, k + 1 | k}^{(l)}), i = 0, 1, \dots, 2 n$ (24)

${\hat{z}}_{k + 1 | k} = \overset{2 n}{\sum_{i = 0}} W_{i}^{m} χ_{_{i, k + 1 | k}}^{(l)}$ （25）

$P_{{\tilde{z}}_{k + 1}}^{(l)} = \overset{n}{\sum_{i = 1}} [W_{i}^{c 1} (χ_{_{i, k + 1 | k}}^{(l)} - χ_{_{i + n, k + 1 | k}}^{(l)})^{2} + W_{i}^{c 2} (χ_{_{i, k + 1 | k}}^{(l)} + χ_{_{i + n, k + 1 | k}}^{(l)} - 2 χ_{_{0, k + 1 | k}}^{(l)})^{2}] + R$ （26）

$P_{{\tilde{x}}_{k + 1} {\tilde{z}}_{k + 1}}^{(l)} = \overset{n}{\sum_{i = 1}} \sqrt[]{W_{i}^{c 1}} [(ξ_{_{i, k + 1 | k}}^{(l)} - {\hat{x}}_{_{k + 1 | k}}) (χ_{_{i, k + 1 | k}}^{(l)} - χ_{_{i + n, k + 1 | k}}^{(l)})^{T}]$ （27）

按照对称采样策略, 利用状态向量预测的统计特性( $\begin{matrix} {\hat{x}}_{k + 1 | k} \end{matrix}$ , P_k+₁_|k)来计算Sigma点:

$\{\begin{matrix} ξ_{0, k + 1 | k} = {\hat{x}}_{k + 1 | k} \\ ξ_{i, k + 1 | k} = {\hat{x}}_{k + 1 | k} + {(h \sqrt[]{P_{k + 1 | k}})}_{i} \\ ξ_{i + n, k + 1 | k} = {\hat{x}}_{k + 1 | k} - {(h \sqrt[]{P_{k + 1 | k}})}_{i} \end{matrix}$ (28)

$\begin{matrix} i = 1, 2, \dots, n \end{matrix}$

ξ _i_,_k+₁_|k通过非线性测量函数传播为χ _i_,_k+₁_|k, 再由χ _i_,_k+₁_|k可得引入渐消因子之后的自协方差矩阵 $\begin{matrix} P_{_{{\tilde{z}}_{k + 1}}} \end{matrix}$ 和互协方差矩阵 $\begin{matrix} P_{_{{\tilde{x}}_{k + 1} {\tilde{z}}_{k + 1}}} \end{matrix}$ , 即:

$χ_{_{i, k + 1 | k}} = h (ξ_{i, k + 1 | k}), i = 0, 1, \dots, 2 n$ (29)

$P_{{\tilde{z}}_{k + 1}} = \overset{n}{\sum_{i = 1}} [W_{i}^{c 1} (χ_{_{i, k + 1 | k}} - χ_{i + n, k + 1 | k})^{2} + W_{i}^{c 2} (χ_{_{i, k + 1 | k}} + χ_{_{i + n, k + 1 | k}} - 2 χ_{_{0, k + 1 | k}})^{2}] + R$ （30）

$P_{{\tilde{x}}_{k + 1} {\tilde{z}}_{k + 1}} = \overset{n}{\sum_{i = 1}} \sqrt[]{W_{i}^{c 1}} [(ξ_{i, k + 1 | k} - {\hat{x}}_{k + 1 | k}) (χ_{_{i, k + 1 | k}} - χ_{_{i + n, k + 1 | k}})^{T}]$ (31)

(2)量测更新

在获得新的量测z_k+₁之后, 进行强跟踪CDKF滤波更新, 即:

${\hat{x}}_{k + 1} = {\hat{x}}_{k + 1 | k} + K_{k + 1} (z_{k + 1} - {\hat{z}}_{k + 1 | k})$ （32）

$K_{k + 1} = P_{{\tilde{x}}_{k + 1} {\tilde{z}}_{k + 1}} P_{{\tilde{z}}_{k + 1}}^{- 1}$ （33）

$\begin{matrix} P_{k + 1} = P_{k + 1 | k} - K_{k + 1} P_{{\tilde{z}}_{k + 1}} {K^{T}}_{k + 1} \end{matrix}$ (34)

3 模型在环仿真验证

为了验证强跟踪CDKF算法对车辆状态和参数估计的可行性和准确性, 在Matlab/Simulink环境下利用车辆动力学仿真软件Carsim进行正弦延迟试验和鱼钩试验。设定强跟踪CDKF算法的状态协方差矩阵初始值为P=I₅_×₅; 系统过程噪声和观测噪声分别为Q=0.001× I₅_×₅和R=[0.005]; 纵向速度、质心侧偏角和横摆角速度的估计初始值取为Carsim软件的初始值; 车辆参数及初始前、后轴等效侧偏刚度如表1所示。

表1 车辆参数 Table 1 Vehicle parameters

3.1 正弦延迟试验

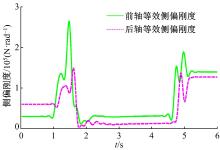
依据报告[17]进行正弦延迟试验, 初始车速为80 km/h, 方向盘转角的峰值为270° 。Carsim软件计算输出的参考值和强跟踪CDKF算法的估计结果如图2所示, 车辆前、后轴等效侧偏刚度参数的估计结果如图3所示。

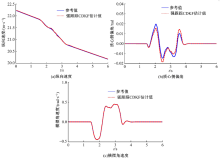	Figure Option View Download New Window
	图2 正弦延迟试验纵向速度、质心侧偏角和横摆角速度估计Fig.2 Longitudinal velocity, side slip angle and yaw rate estimation of sine with dwell test

	Figure Option View Download New Window
	图3 正弦延迟试验侧偏刚度估计Fig.3 Lateral stiffness estimation of sine with dwell test

结果表明, 对于纵向速度和横摆角速度, 强跟踪CDKF算法取得了较好的估计效果; 对于质心侧偏角, 该算法的估计结果与参考值之间存在一定偏差。车辆速度较快时执行快速转向动作, 较大的车辆侧倾运动以及轮胎进入非线性工作区域会导致轮胎外倾角、侧偏角和载荷摄动, 而这些因素直接影响车辆标称模型的前、后轴等效侧偏刚度, 故图3所示强跟踪CDKF算法对前、后轴等效侧偏刚度估计结果与理论分析一致。

3.2 鱼钩试验

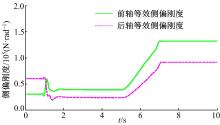
依据报告[17]进行鱼钩试验, 初始车速为90 km/h, 方向盘转角的峰值为240° 。Carsim软件计算输出的参考值和强跟踪CDKF算法的估计结果如图4所示, 车辆前后轴等效侧偏刚度参数的估计结果如图5所示。

	Figure Option View Download New Window
	图4 鱼钩试验纵向速度、质心侧偏角和横摆角速度估计Fig.4 Longitudinal velocity, side slip angle and yaw rate estimation of fishhook test

	Figure Option View Download New Window
	图5 鱼钩试验侧偏刚度估计Fig.5 Lateral stiffness estimation of fishhook test

结果表明, 强跟踪CDKF算法对于纵向速度和横摆角速度的估计取得了较好的效果, 而估计的质心侧偏角与参考值之间存在一定偏差。同时, 根据3.1节的分析, 图5所示强跟踪CDKF算法对标称模型的前、后轴等效侧偏刚度估计结果与理论分析一致。

前述两种试验工况下, 在利用强跟踪CDKF算法进行车辆状态估计时, 对车辆标称模型的前后轴等效侧偏刚度并行估计, 有效抑制标称模型的不确定性、短时外界扰动和系统状态量初始值估计偏差较大对车辆状态估计结果的影响, 提高系统状态量的估计精度, 增加系统的鲁棒性。

4 硬件在环仿真验证

为了进一步验证强跟踪CDKF算法对车辆状态和参数估计的实时性和有效性, 采用dSPACE公司的多核处理器板DS1006和外围I/O板, 以及Carsim软件构建硬件在环仿真系统, 利用Matlab软件的实时工作间技术将强跟踪CDKF算法与Carsim软件联合仿真模型编译成实时运行的硬件代码, 并将其无缝下载至处理器板DS1006。试验环境如图6所示。

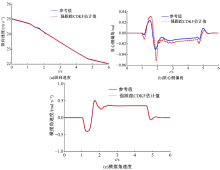
	Figure Option View Download New Window
	图6 试验环境Fig.6 Experiment environment

依据报告[17]进行J-Turn试验, 初始车速为80 km/h, 方向盘转角的峰值为200° 。Carsim软件计算输出的参考值和强跟踪CDKF算法的估计结果如图7所示, 车辆前、后轴等效侧偏刚度参数的估计结果如图8所示。

硬件在环结果表明, 实时运行的强跟踪CDKF算法对于车辆的纵向速度和横摆角速度取得了较好的估计效果; 但对于车辆的质心侧偏角的估计, 该算法的输出结果与参考值之间存在一定偏差。同时, 硬件在环仿真结果与模型在环仿真结果具有较好的一致性。

	Figure Option View Download New Window
	图7 J-Turn试验纵向速度、质心侧偏角和横摆角速度估计Fig.7 Longitudinal velocity, side slip angle and yaw rate estimation of J-Turn test

	Figure Option View Download New Window
	图8 J-Turn试验侧偏刚度估计Fig.8 Lateral stiffness estimation of J-Turn test

5 结束语

利用强跟踪CDKF算法对车辆的纵向速度、质心侧偏角与横摆角速度等信息进行估计, 算法不需要计算雅可比矩阵, 易于实时实现。模型在环和硬件在环仿真结果表明, 采用该算法在对车辆状态进行估计时, 并行估计标称模型的前、后轴等效侧偏刚度, 可提高状态量的估计精度, 且对标称模型的不确定性和外界扰动等因素具有强鲁棒性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	郭洪艳, 陈虹, 赵海燕, 等. 汽车行驶状态参数估计研究进展与展望[J]. 控制理论与应用, 2013, 30(6): 661-672. Guo Hong-yan, Chen Hong, Zhao Hai-yan, et al. State and parameter estimation for running vehicle recent developments and perspective[J]. Control Theory & Applications, 2013, 30(6): 661-672. [本文引用:1]
[2]	Xin X, Chen J, Zou J. Vehicle state estimation using cubature Kalman filter[J]. Vehicle System Dynamics: International Journal of Vehicle Mechanics and Mobility, 2014, 49(9): 1497-1520. [本文引用:1]
[3]	武冬梅, 丁海涛, 郭孔辉. 基于线性估计模型的电动汽车质心侧偏角估计[J]. 吉林大学学报: 工学版, 2014, 44(4): 901-906. Wu Dong-mei, Ding Hai-tao, Guo Kong-hui. Sideslip angle estimation based on linear estimation model for electric vehicle[J]. Journal of Jilin University(Engineering and Technology Edition), 2014, 44(4): 901-906. [本文引用:1]
[4]	Mario H, Josko D, Danijel P, et al. Adaptive EKF-based estimator of sideslip angle using fusion of inertial sensors and GPS[C]∥SAE Paper, 2011 -01-0953, 2011. [本文引用:1]
[5]	Ungoren A Y, Huei P, Tseng H E. A study on lateral speed estimation methods[J]. International Journal on Vehicle Autonomous Systems, 2004, 2(1/2): 126-144. [本文引用:1]
[6]	Grip H F, Imsland L, Johansen T A. Nonlinear vehicle side slip estmation with friction adaptation[J]. Automatica, 2008, 44: 611-622. [本文引用:1]
[7]	Shraim H, Ouladsine M, Fridman L. Vehicle parameters and states estimation via sliding mode observers[J]. SpringerLink, 2008, 375: 345-362. [本文引用:1]
[8]	赵林辉, 刘志远, 陈虹. 车速和路面附着系数的滚动时域估计[J]. 汽车工程, 2009, 31(6): 520-525. Zhao Lin-hui, Liu Zhi-yuan, Chen Hong. The estimation of vehicle speed and tire-road adhesion coefficient using moving horizon strategy[J]. Automotive Engineering, 2009, 31(6): 520-525. [本文引用:1]
[9]	Darby M L, Nikolaou M. A parametric programming approach to moving horizon state estimation[J]. Automatica, 2007, 43(5): 885-891. [本文引用:1]
[10]	Antonov S, Fehn A, Kugi A. Unscented Kalman filter for vehicle state estimation[J]. Vehicle System Dynamics: International Journal of Vehicle Mechanics and Mobility, 2011, 49(9): 1497-1520. [本文引用:1]
[11]	Sun F, Huang X H, Joachim R, et al. Vehicle state estimation for anti-lock control with nonlinear observer[J]. Control Engineering Practice, 2015, 43: 69-84. [本文引用:1]
[12]	Zhang H, Huang X, Wang J, et al. Robust energy-to-peak sideslip angle estimation with applications to ground vehicles[J]. Mechatronics, 2015, 30: 338-347. [本文引用:1]
[13]	王小旭, 赵琳, 薛红香. 强跟踪CDKF及其在组合导航中的应用[J]. 控制与决策, 2010, 25(12): 1837-1842. Wang Xiao-xu, Zhao Lin, Xue Hong-xiang. Strong tracking CDKF and application for integrated navigation[J]. Control and Decision, 2010, 25(12): 1837-1842. [本文引用:1]
[14]	Nrgarrd M, Poulsen N K, Ravn O. New developments in state estimation for nonlinear systems[J]. Automatica, 2000, 36(11): 1627-1638. [本文引用:1]
[15]	郭孔辉. 汽车操纵动力学原理[M]. 南京: 江苏科技技术出版社, 2011: 172-178. [本文引用:1]
[16]	Zhou D H, Xi Y G, Zhang Z J. A suboptimal multiple extended Kalman filter[J]. Chinese Journal of Automation, 1992, 4(2): 145-152. [本文引用:1]
[17]	National Highway Traffic Safety Administration. A comprehensive experimental examination of test maneuvers that may induce on-road, untripped, light vehicle rollover-phase IV of NHTSA's light vehicle rollover research program[R]. Washington, 2002. [本文引用:1]

2013

0.0

. 2013, 30(6):661-672 DOI:doi:10.7641/CTA.2013.21190

State and parameter estimation for running vehicle recent developments and perspective

汽车行驶状态参数估计研究进展与展望

Guo Hong-yan , Chen Hong , Zhao Hai-yan

郭洪艳, 陈虹, 赵海燕

准确而实时地获得汽车的行驶状态参数信息是实现汽车主动安全控制的关键问题,也是车载故障诊断的重要技术之一.随着估计理论的发展,利用车辆上已装备的传感器获得汽车行驶状态信息,进行汽车行驶状态参数估计是近年来的研究热点.本文首先给出汽车系统中需要进行估计的状态参数的分类及现有估计方案;然后对现有的各种汽车行驶状态参数估计方法加以综述,并分析了各种方法在汽车行驶状态参数估计方面的优缺点;最后对汽车行驶状态参数估计的进一步研究提出几点展望.

... 0 引言准确实时获得汽车行驶过程中的状态信息是汽车主动安全控制领域的关键问题之一,也是实现闭环反馈控制的前提和必要条件^[1] ...

2014

0.0

... 但由于技术和成本方面的原因,这些信息通常无法直接测量,而由此衍生出来的利用车载传感器测量得到的信息来实时估计汽车行驶过程中的纵向速度、质心侧偏角等状态信息成为近年来国内外研究的热点^[2,3] ...

2014

0.0

. 2014, 44(4):901-906 DOI:doi:10.13229/j.cnki.jdxbgxb201404001

Sideslip angle estimation based on linear estimation model for electric vehicle

基于线性估计模型的电动汽车质心侧偏角估计

Wu Dong-mei , Ding Hai-tao , Guo Kong-hui.

武冬梅, 丁海涛, 郭孔辉

Sideslip angle estimation is the key technique of vehicle stability control system. For electric vehicle, the information of driving torque and braking torque on wheels can be fully utilized to calculate the longitudinal force on the tire. If the longitudinal slip of the tire is large enough, the lateral force on the tire can be expressed with the longitudinal force on the tire and the tire slip angle. If the longitudinal slip of the tire is small, the nonlinear tire model is locally linearized. In such way, the two degrees of freedom vehicle model can be simplified to a linear model, whose state variable is the vehicle lateral speed and can be used to estimate the sideslip angle of the vehicle. Simulation results show that the estimation accuracy of the sideslip angle with the linear estimation model is high enough, and its dependence on the road surface friction coefficient is small. In addition, the calculation is simple due to the linearity of the model. The estimation method can be applied to the vehicle stability control system.

质心侧偏角估计是车辆稳定性控制系统中的关键技术和难点, 针对电动汽车, 本文充分利用车轮上的驱动力矩和制动力矩信息, 计算出了轮胎上的纵向力。并将轮胎侧向力用纵向力和侧偏角表示或进行局部线性化。这样可以将二自由度车辆模型简化为以侧向速度为状态的线性估计模型, 用于电动汽车质心侧偏角的估计。仿真结果表明:基于线性估计模型的质心侧偏角估计器的估计精度较高, 对路面摩擦因数的依赖程度小, 并且计算简单, 可以应用于车辆的稳定性控制系统中。

2011

0.0

... 目前较为常用的汽车状态估计算法主要有扩展卡尔曼滤波器^[4,5],状态观测器估计算法^[6,7]和滚动时域优化估计算法^[8,9]等 ...

2004

0.0

... 目前较为常用的汽车状态估计算法主要有扩展卡尔曼滤波器^[4,5],状态观测器估计算法^[6,7]和滚动时域优化估计算法^[8,9]等 ...

2008

0.0

... 目前较为常用的汽车状态估计算法主要有扩展卡尔曼滤波器^[4,5],状态观测器估计算法^[6,7]和滚动时域优化估计算法^[8,9]等 ...

2008

0.0

... 目前较为常用的汽车状态估计算法主要有扩展卡尔曼滤波器^[4,5],状态观测器估计算法^[6,7]和滚动时域优化估计算法^[8,9]等 ...

2009

0.0

. 2009, 31(6):520-525

The estimation of vehicle speed and tire-road adhesion coefficient using moving horizon strategy

车速和路面附着系数的滚动时域估计

Zhao Lin-hui , Liu Zhi-yuan , Chen Hong.

赵林辉, 刘志远, 陈虹

... 目前较为常用的汽车状态估计算法主要有扩展卡尔曼滤波器^[4,5],状态观测器估计算法^[6,7]和滚动时域优化估计算法^[8,9]等 ...

2007

0.0

... 目前较为常用的汽车状态估计算法主要有扩展卡尔曼滤波器^[4,5],状态观测器估计算法^[6,7]和滚动时域优化估计算法^[8,9]等 ...

2011

0.0

2015

0.0

2015

0.0

2010

0.0

. 2010, 25(12):1837-1842

Strong tracking CDKF and application for integrated navigation

强跟踪CDKF及其在组合导航中的应用

Wang Xiao-xu , Zhao Lin , Xue Hong-xiang.

王小旭, 赵琳, 薛红香

A central difference Kalman filter(CDKF) with strong tracking behavior is proposed to overcome the problemthat extended Kalman filter(EKF) decreases in accuracy, even divergences when integrated navigation system has modeluncertainty. Strong tracking CDKF views strong tracking filter(STF) as the basic theory framework and makes centraldifference transformation take place of calculating nonlinear function Jacobian matrix, so it combines strong robustness ofSTF with high accuracy and easy implementation of central difference transformation. The proposed strong tracking CDKFcan avoid filtering failure of EKF while system model is uncertain. Simulation results show the effectiveness of the strongtracking CDKF.

... 强跟踪中心差分卡尔曼滤波器(Strong central difference Kalman filter,CDKF)基于强跟踪滤波器理论框架,采用中心差分变换以二阶泰勒精度逼近非线性高斯系统状态的后验均值和协方差,无需计算非线性函数的雅克比矩阵,且兼具强跟踪滤波器鲁棒性强的特点^[13,14] ...

2000

0.0

2011

0.0

... 过原点与X_v轴垂直的方向规定为Y_v轴,向左为正^[15] ...

1992

0.0

... 2 强跟踪中心差分卡尔曼滤波器强跟踪CDKF使用正交性原理,通过在状态预测协方差矩阵中引入渐消因子的方法,强迫输出残差具有正交性或近似正交性,从而对系统的突变状态具有跟踪能力^[16] ...

2002

0.0