数控机床转台位置相关几何误差的快速测量与辨识

doi:10.13229/j.cnki.jdxbgxb20200031

摘要/Abstract

摘要：

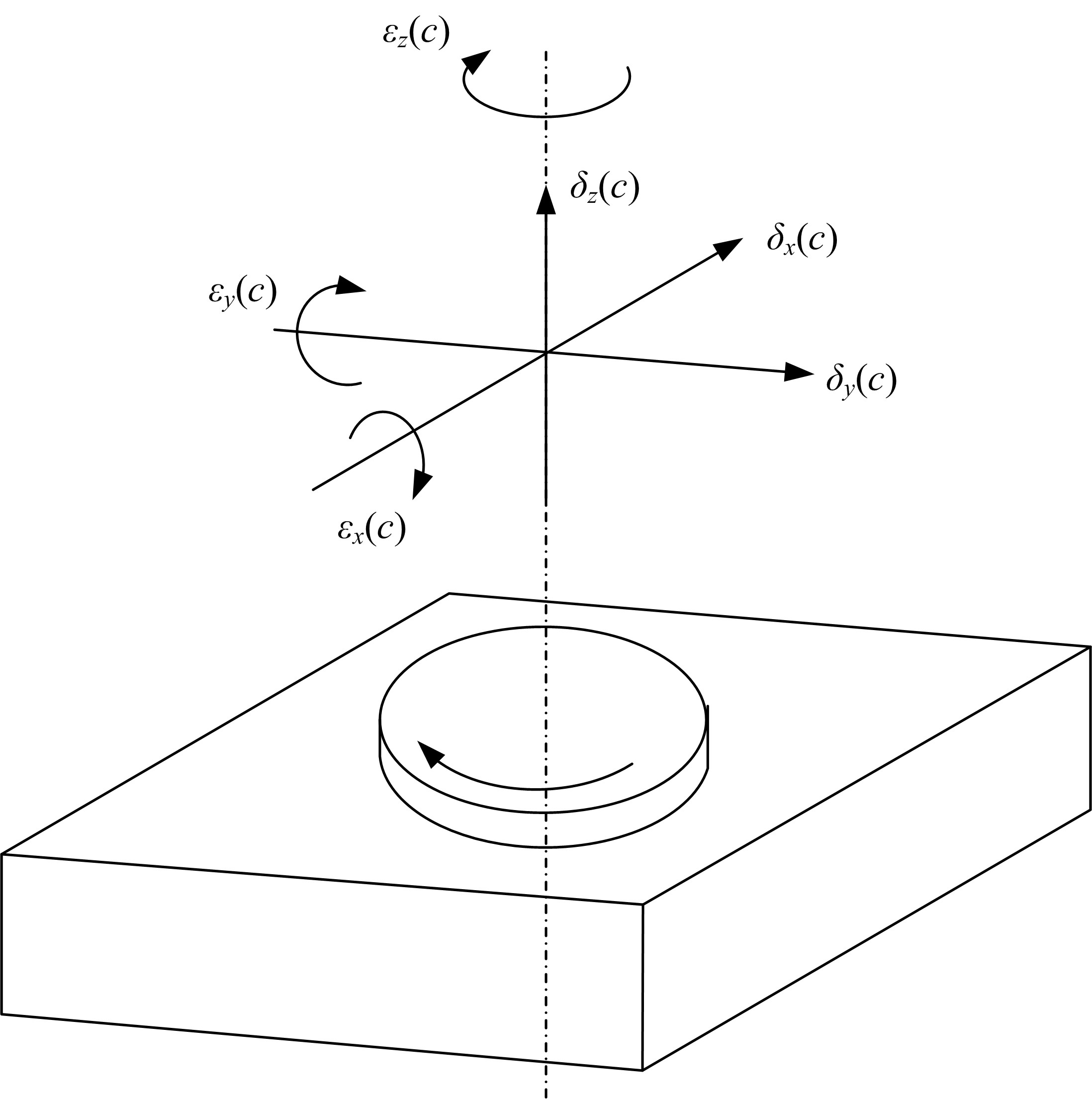
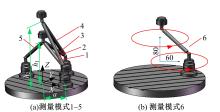
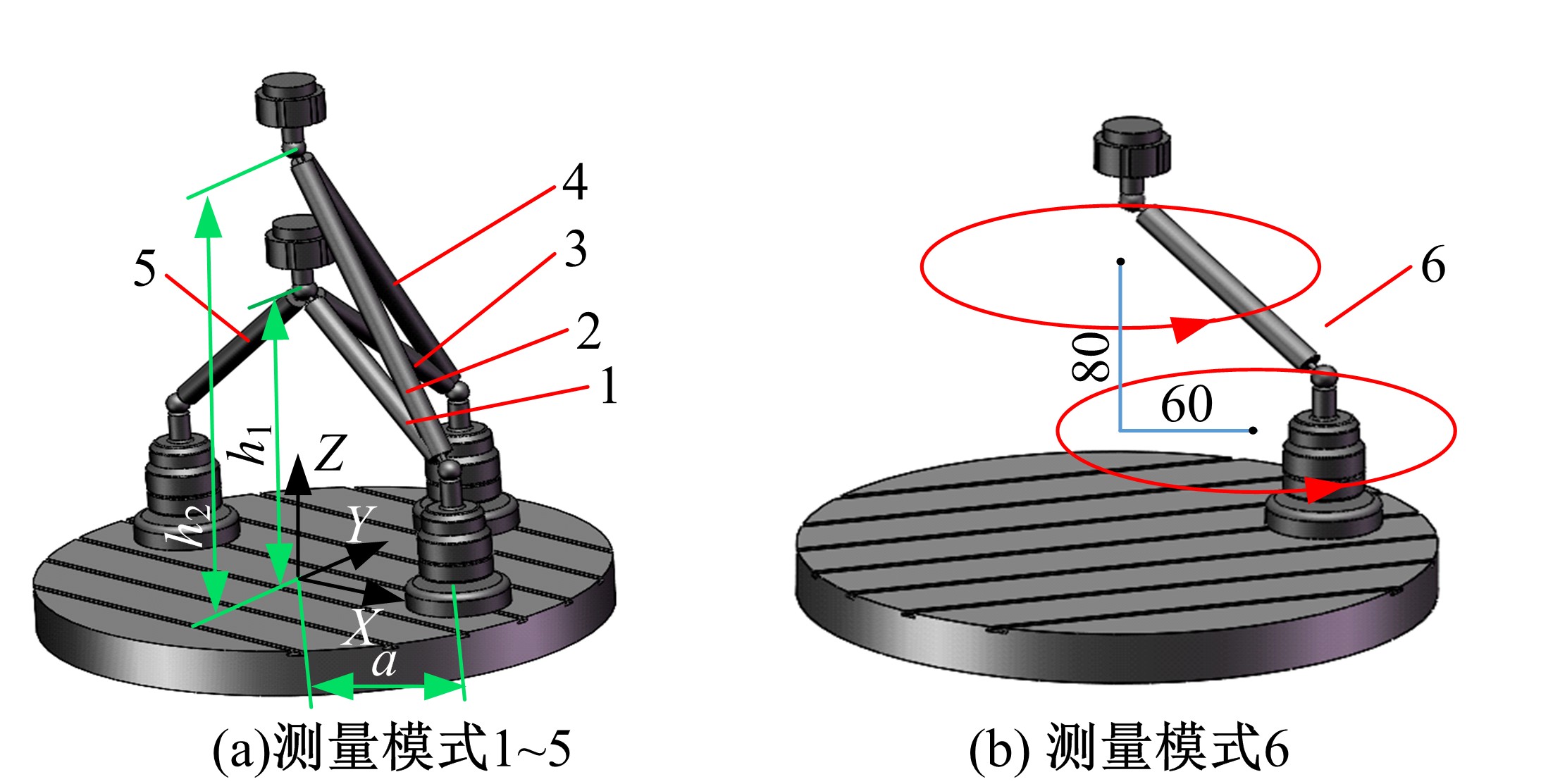
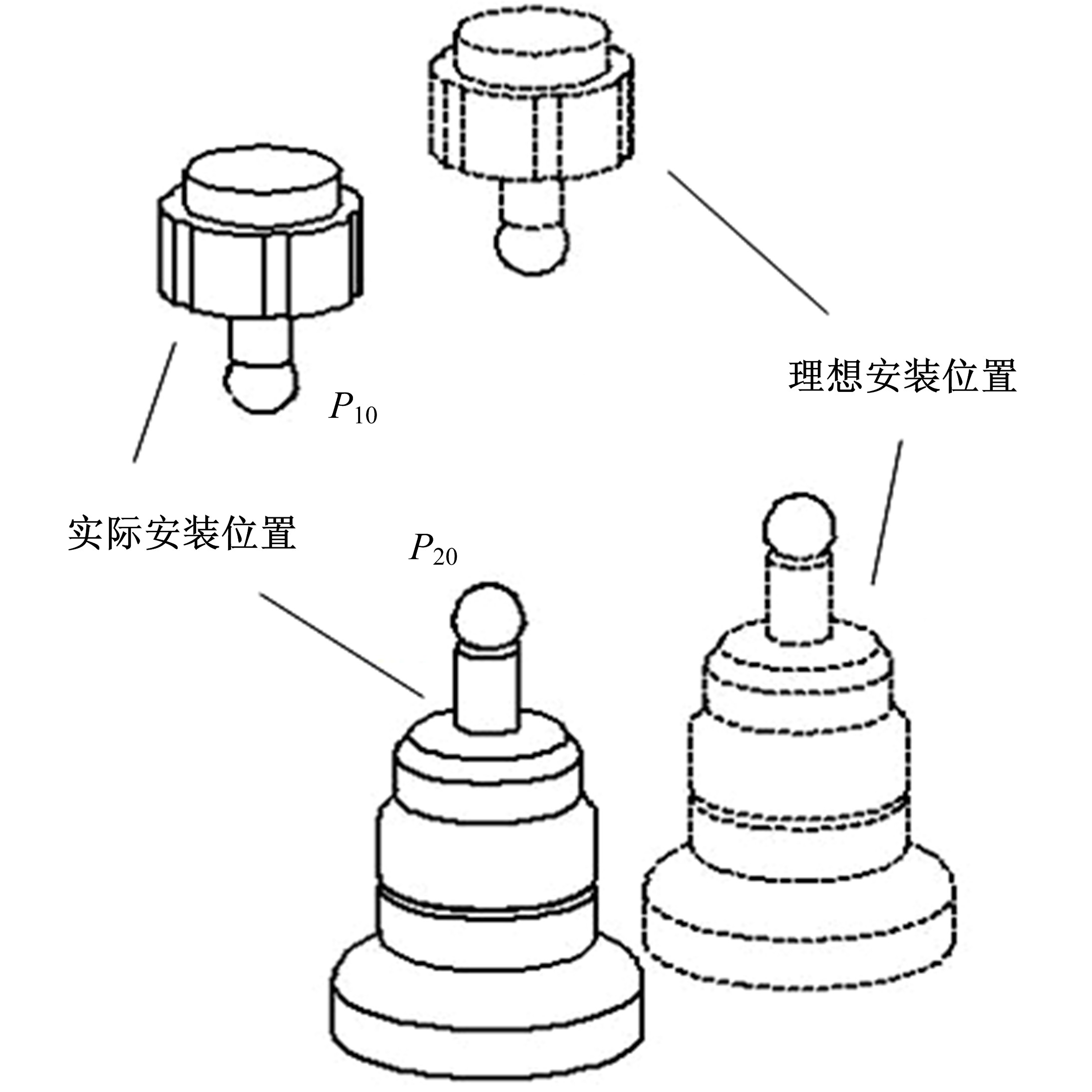
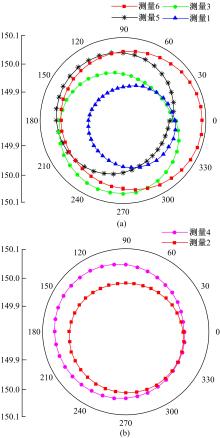
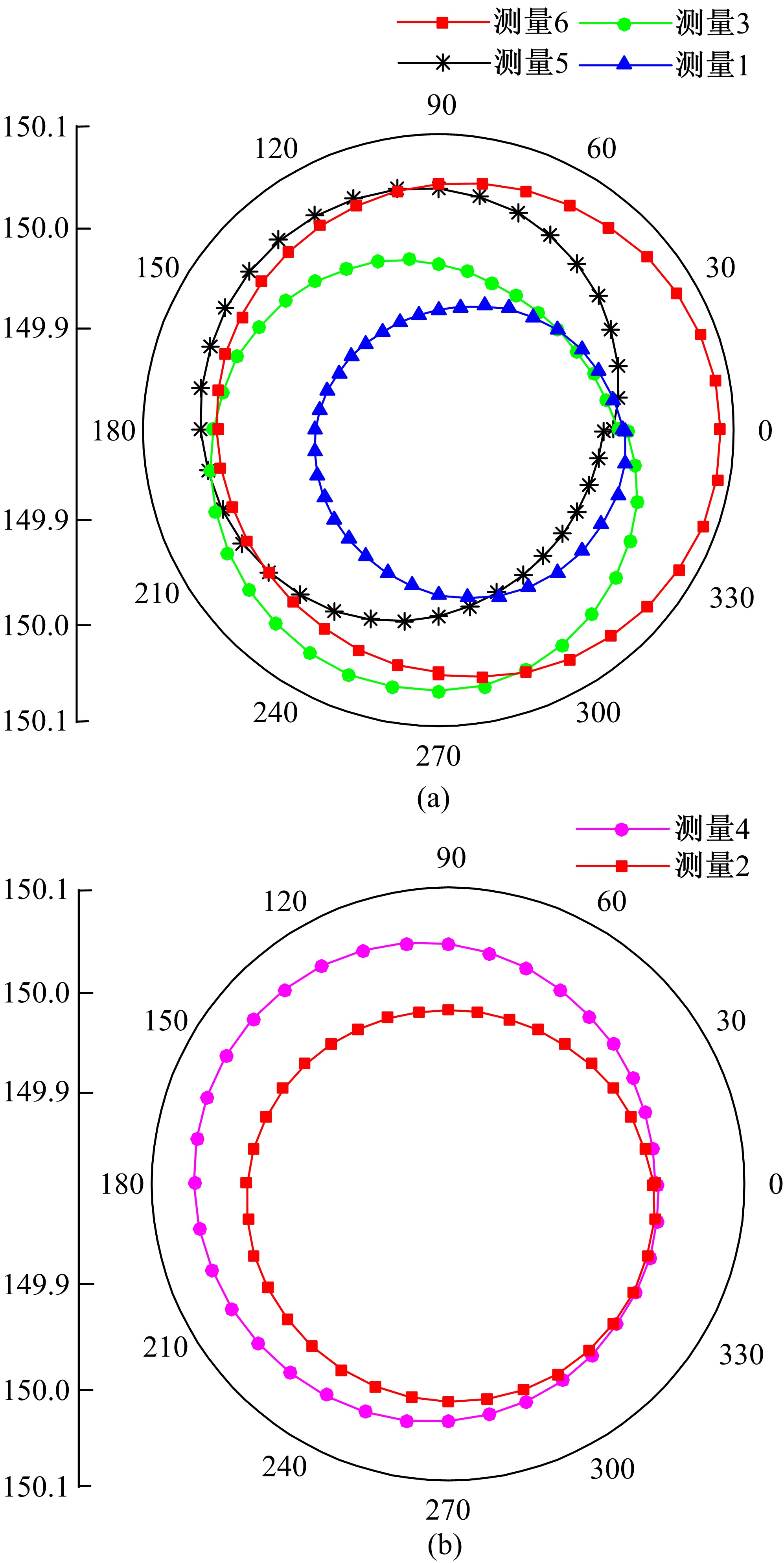
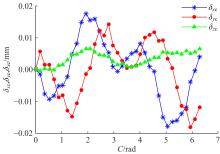
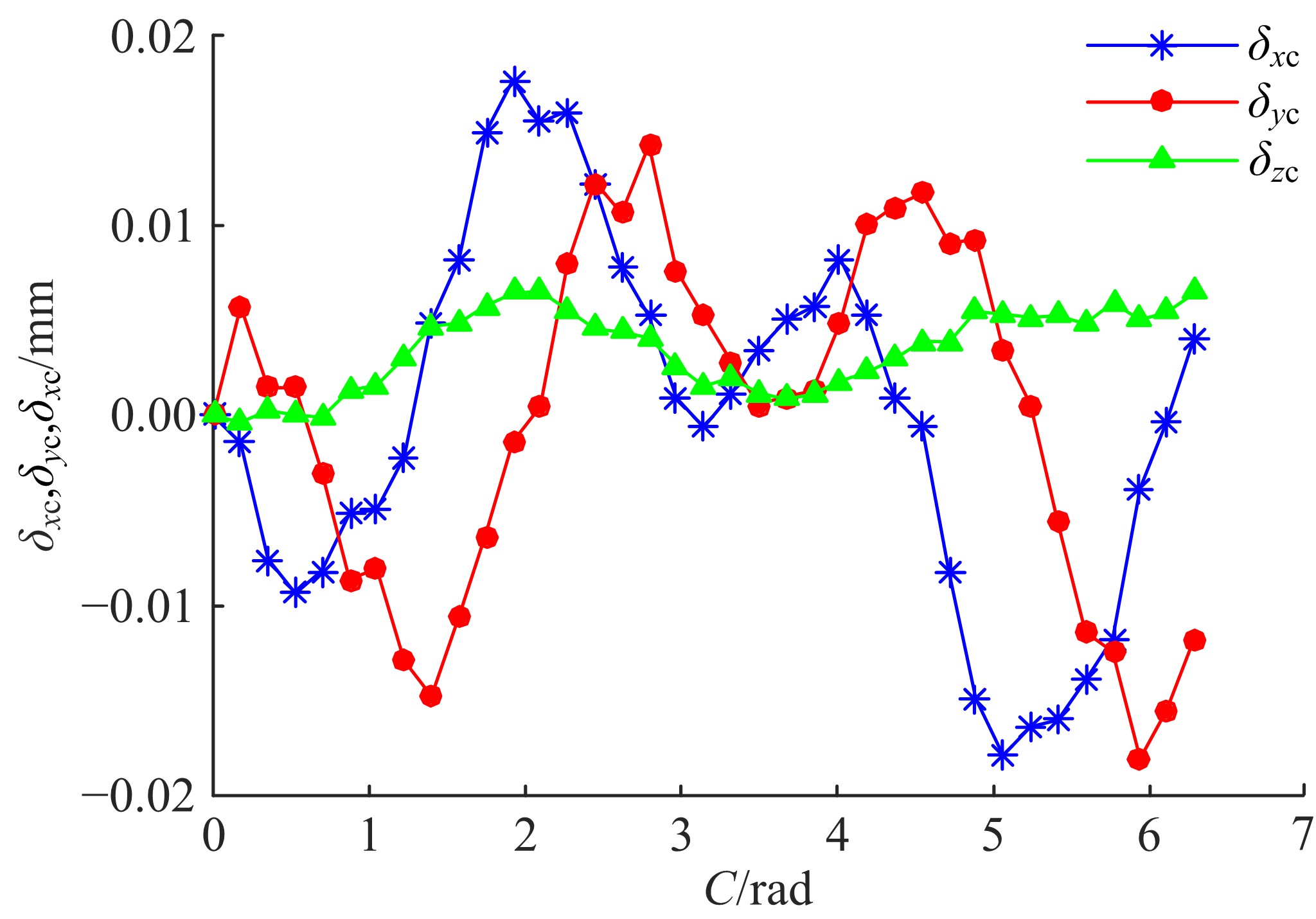
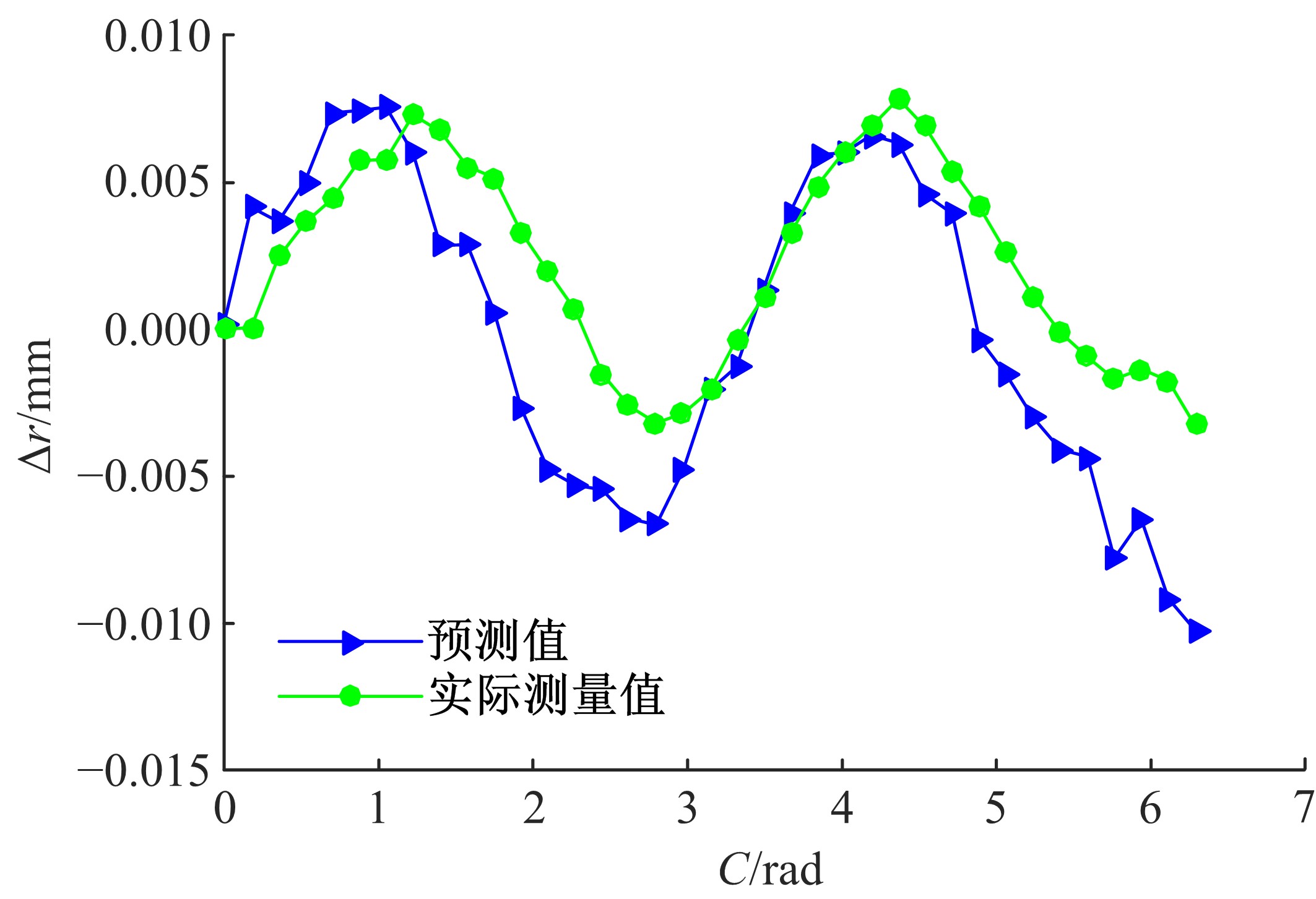
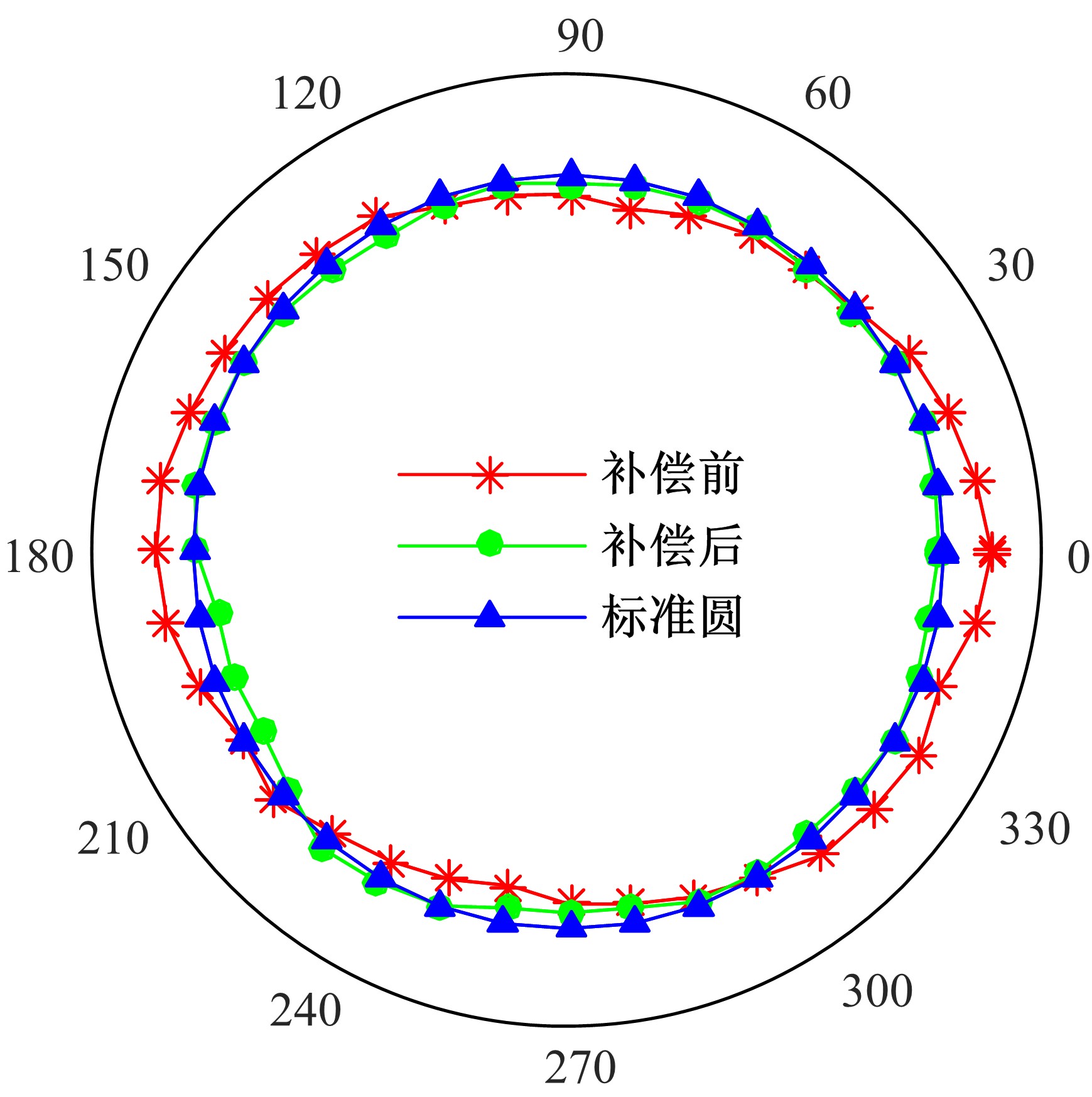
为快速辨识数控机床转台位置相关几何误差，提出一种基于球杆仪的转台位置相关几何误差快速测量辨识方法。首先，基于齐次坐标变换建立转台位置相关几何误差模型，得到球杆仪杆长变化量与几何误差的关系；其次，设计球杆仪六次锥形安装方式，推导出误差辨识矩阵，记录球杆仪杆长变化量，快速辨识出转台位置相关几何误差，并提出一种球杆仪安装误差消除方法，有效剔除了安装误差的影响；最后，基于转台位置相关几何误差的辨识结果，对附加实验中球杆仪杆长变化量进行预测，预测精度较高；在此基础上，对转台位置相关几何误差进行补偿，补偿后的精度明显提高。结果表明：该方法可准确快速辨识出数控机床转台位置相关几何误差，对提高机床精度具有重要的意义。

关键词: 机械制造及其自动化, 数控机床转台, 位置相关几何误差, 球杆仪, 安装误差

Abstract:

In order to quickly and systematically identify the position dependent geometric error terms of CNC machine tool turntable， a rapid measurement and identification method of the geometric error of the turntable based on a double ballbar is proposed. Firstly， based on the homogeneous coordinate transformation theory， the position dependent geometric error model of the machine tool turntable is established， and the relationship between the change in ballbar length and the geometric error during the movement of the ballbar is obtained. Then， a six-time tapered installation method of the ballbar is designed， the error identification matrix expression is direved， the change in the length of the ballbar during the movement of the ballbar is record， and the position dependent geometric error terms of the turntable can be quickly identified. Then， a method for eliminating the installation error of the double ballbar is proposed， which can effectively eliminate the influence of the installation error in the raw data of the ballbar measurement. Finally， based on the identification results of the position dependent geometric errors of the turntable， the change in the length of the ballbar in the additional experiment is predicted， and compared with the experimental results， the prediction accuracy is high. On this basis， the position dependent geometric error of the turntable is compensated. It is show that after compensation， the accuracy is significantly improved compared with that before compensation. The experimental results show that the method can accurately and quickly identify the position dependent geometric error terms of the turntable， which has important significance for improving the accuracy of the machine tool.

Key words: mechanical manufacturing and automation, CNC machine tool turntable, position dependent geometric errors, the double ballbar, installation error

中图分类号:

TH161

李国龙,陶小会,徐凯,李喆裕. 数控机床转台位置相关几何误差的快速测量与辨识[J]. 吉林大学学报(工学版), 2021, 51(2): 458-467.

Guo-long LI,Xiao-hui TAO,Kai XU,Zhe-yu LI. Rapid measurement and identification of position dependent geometric errors of CNC machine tool turntable[J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(2): 458-467.

图/表 14

图1

图2

图3

图4

表1

表2

表3

表4

图5

图6

图7

图8

图9

图10

参考文献 24

1	杨建国, 范开国, 杜正春. 数控机床误差实时补偿技术[M]. 北京: 机械工业出版社, 2013.
2	Abbaszadeh-Mir Y, Mayer J R R, Cloutier G, et al. Theory and simulation for the identification of the link geometric errors for a five-axis machine tool using a telescoping magnetic ball-bar[J]. International Journal of Production Research, 2002, 40(18): 4781-4797.
3	. Test code for machine tools—part 7: geometric accuracy of axes of rotation[S].
4	Zargarbashi S H H, Mayer J R R. Single setup estimation of a five-axis machine tool eight link errors by programmed end point constraint and on the fly measurement with capball sensor[J]. International Journal of Machine Tools and Manufacture, 2009, 49(10): 759-766.
5	Wang M, Hu J Z, Zan T. Kinematic error separation on five-axis NC machine tool based on telescoping double ball bar[J]. Frontiers of Mechanical Engineering, 2010, 5(4): 431-437.
6	He Z, Fu J, Zhang L, et al. A new error measurement method to identify all six error parameters of a rotational axis of a machine tool[J]. International Journal of Machine Tools and Manufacture, 2015, 88: 1-8.
7	Hong C, Ibaraki S, Oyama C. Graphical presentation of error motions of rotary axes on a five-axis machine tool by static R-test with separating the influence of squareness errors of linear axes[J]. International Journal of Machine Tools and Manufacture, 2012, 59: 24-33.
8	Ibaraki S, Oyama C, Otsubo H. Construction of an error map of rotary axes on a five-axis machining center by static R-test[J]. International Journal of Machine Tools and Manufacture, 2011, 51(3): 190-200.
9	Bi Q, Huang N, Sun C, et al. Identification and compensation of geometric errors of rotary axes on five-axis machine by on-machine measurement[J]. International Journal of Machine Tools and Manufacture, 2015, 89: 182-191.
10	Ibaraki S, Iritani T, Matsushita T. Calibration of location errors of rotary axes on five-axis machine tools by on-the-machine measurement using a touch-trigger probe[J]. International Journal of Machine Tools and Manufacture, 2012, 58: 44-53.
11	Uddin M S, Ibaraki S, Matsubara A, et al. Prediction and compensation of machining geometric errors of five-axis machining centers with kinematic errors[J]. Precision Engineering, 2009, 33(2): 194-201.
12	Xiang S, Yang J, Zhang Y. Using a double ball bar to identify position-independent geometric errors on the rotary axes of five-axis machine tools[J]. The International Journal of Advanced Manufacturing Technology, 2014, 70(9-12): 2071-2082.
13	Zhang Y, Yang J, Zhang K. Geometric error measurement and compensation for the rotary table of five-axis machine tool with double ballbar[J]. International Journal of Advanced Manufacturing Technology, 2013, 65(1-4): 275-281.
14	Zargarbashi S H H, Mayer J R R. Assessment of machine tool trunnion axis motion error, using magnetic double ball bar[J]. International Journal of Machine Tools and Manufacture, 2006, 46(14): 1823-1834.
15	Tsutsumi M, Tone S, Kato N, et al. Enhancement of geometric accuracy of five-axis machining centers based on identification and compensation of geometric deviations[J]. International Journal of Machine Tools and Manufacture, 2013, 68(5): 11-20.
16	Lee K I, Lee D M, Yang S H. Parametric modeling and estimation of geometric errors for a rotary axis using double ball-bar[J]. International Journal of Advanced Manufacturing Technology, 2012, 62(5-8): 741-750.
17	徐凯, 李国龙, 何坤, 等. 基于球杆仪的直线轴位置相关误差辨识研究[J]. 仪器仪表学报, 2019, 40(5): 1-9.
	Xu Kai, Li Guo-long, He Kun, et. al. Research on dependent error identification of linear axes based on double ball-bar[J]. Chinese Journal of Scientific Instrument, 2019, 40(5): 1-9.
18	付国强, 傅建中, 沈洪垚. 五轴数控机床旋转轴几何误差辨识新方法[J]. 浙江大学学报: 工学版, 2015, 49(5): 848-857.
	Fu Guo-qiang, Fu Jian-zhong, Shen Hong-yao. One novel geometric error identification of rotary axes for five-axis machine tool[J]. Journal of Zhejiang University (Engineering Science), 2015, 49(5): 848-857.
19	郭世杰, 姜歌东, 梅雪松. 摆头转台型五轴机床旋转轴运动误差测量与辨识[J]. 农业机械学报, 2019, 50(2): 402-410, 426.
	Guo Shi-jie, Jiang Ge-dong, Mei Xue-song. Motion error measurement and identification of rotary axis of five-axis machine tool[J]. Transactions of the Chinese Society for Agricultural Machinery, 2019, 50(2): 402-410, 426.
20	Ding S, Wu W, Huang X, et al. Single-axis driven measurement method to identify position-dependent geometric errors of a rotary table using double ball bar[J]. The International Journal of Advanced Manufacturing Technology, 2019,101(5-8): 1715-1724.
21	Zhu S, Ding G, Qin S, et al. Integrated geometric error modeling, identification and compensation of CNC machine tools[J]. International Journal of Machine Tools & Manufacture, 2012, 52(1): 24-29.
22	刘志峰, 刘广博, 程强, 等. 基于多体系统理论的精密立式加工中心精度建模与预测[J]. 吉林大学学报: 工学版, 2012, 42(2): 388-391.
	Liu Zhi-feng, Liu Guang-bo, Cheng Qiang, et al. Precision modeling and prediction of precise vertical machining center based on theory of multi-body system[J]. Journal of Jilin University (Engineering and Technology Edition), 2012, 42(2): 388-391.
23	曲兴田, 赵永兵, 刘海忠, 等. 基串并混联机床几何误差建模与实验[J]. 吉林大学学报: 工学版, 2017, 47(1): 137-144.
	Qu Xing-tian, Zhao Yong-bing, Liu Hai-zhong, et al. Modeling and experiment of spatial geometric errors of hybrid serial parallel machine tool[J]. Journal of Jilin University (Engineering and Technology Edition), 2017, 47(1): 137-144.
24	Lee K I, Yang S H. Measurement and verification of position-independent geometric errors of a five-axis machine tool using a double ball-bar[J]. International Journal of Machine Tools and Manufacture, 2013, 70(4): 45-52.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

测量模式	拟合圆半径
测量模式	计算值/mm	仿真值/mm	差值/mm
1	100.0480	100.0453	0.0027
2	150.0498	150.0431	0.0067
3	100.0520	100.0458	0.0062
4	150.0525	150.0438	0.0087
5	100.0480	100.0453	0.0027
6	100.0514	100.0593	-0.0079

测量模式	拟合圆圆心x坐标
测量模式	计算值/mm	仿真值/mm	差值/mm
1	-0.0400	-0.0333	-0.0067
2	-0.0267	-0.0184	-0.0083
3	-0.0480	-0.0503	0.0023
4	-0.0320	-0.0367	0.0047
5	-0.0400	-0.0336	-0.0064
6	-0.0295	-0.0360	0.0065

测量模式	拟合圆圆心y坐标
测量模式	计算值/mm	仿真值/mm	差值/mm
1	-0.0480	-0.0550	0.0070
2	-0.0320	-0.0437	0.0117
3	0.0400	0.0289	0.0111
4	0.0267	0.0123	0.0144
5	-0.0400	-0.0489	0.0089
6	-0.0386	-0.0300	-0.0086

测量	刀具球P₁	工件球P₂
1	（0,0,60）	（80,0,0）
2	（0,0,126.886）	（80,0,0）
3	（0,0,60）	（0,80,0）
4	（0,0,126.886）	（0,80,0）
5	（0,0,60）	（-80,0,0）
6	（-60,80,80）	（0,80,0）

[1]	段春争,张方圆,寇文能,魏斌. 高速硬切削表面白层马氏体相变[J]. 吉林大学学报(工学版), 2019, 49(5): 1575-1583.
[2]	刘国政, 史文库, 陈志勇. 考虑安装误差的准双曲面齿轮传动误差有限元分析[J]. 吉林大学学报(工学版), 2018, 48(4): 984-989.