Journal of Jilin University(Engineering and Technology Edition) ›› 2023, Vol. 53 ›› Issue (7): 1911-1919.doi: 10.13229/j.cnki.jdxbgxb.20211023

Previous Articles    

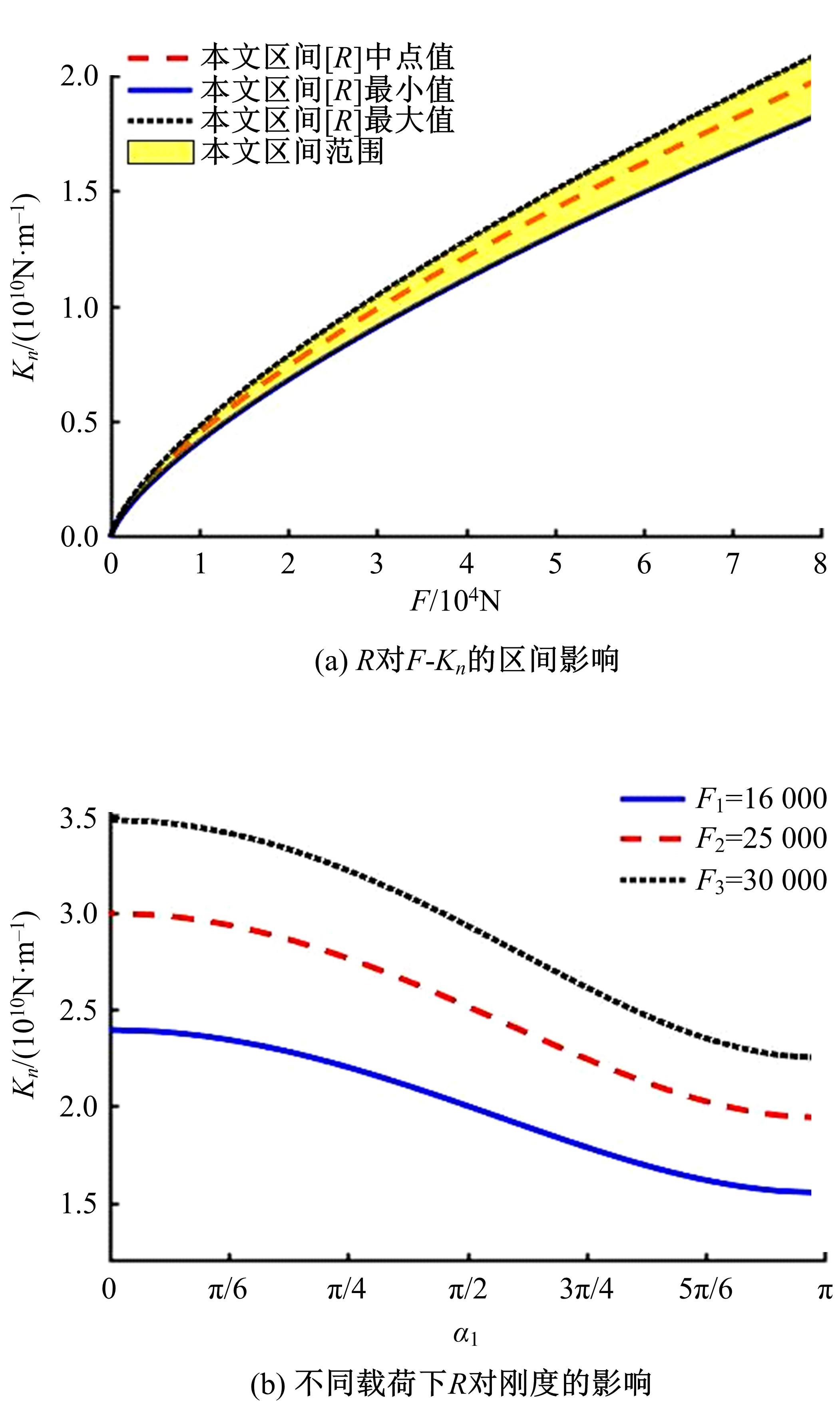
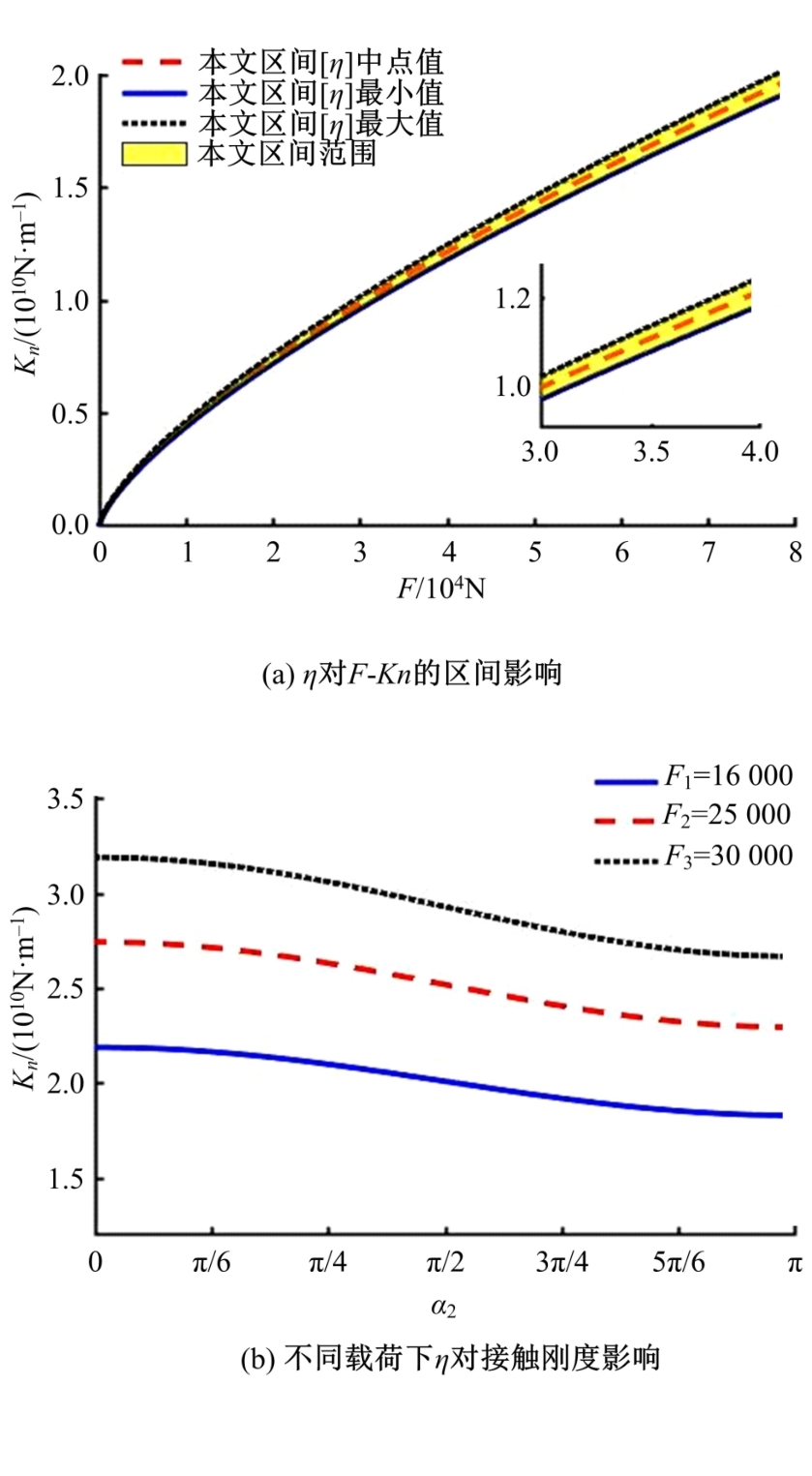
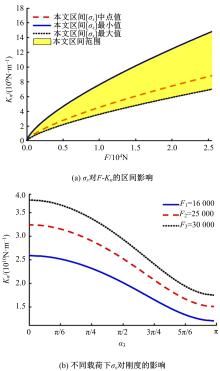
Uncertainty quantification of normal contact stiffness of bolt joint surface

Ling LI(),Kai ZHAO,Hong LIN(),Jing-jing WANG,An-jiang CAI   

  1. School of Mechanical and Electrical Engineering，Xi'an University of Architecture and Technology，Xi'an 710055，China
  • Received:2021-10-27 Online:2023-07-01 Published:2023-07-20
  • Contact: Hong LIN E-mail:liling@xauat.edu.cn;lh759@163.com

RICH HTML

 1   

PDF (PC)

342

Abstract:

There are many uncertainties in the contact of bolted joints. It is difficult to determine the reasonable interval of contact stiffness in existing models. Therefore， the range of contact stiffness of joint surface with uncertain micromorphology is obtained by using interval Estimation theory. Firstly， based on fractal theory to characterize the contour height of the micro-convex body of the combined surface， the structural function method and interval algorithm are used to solve the uncertainty interval of the fractal parameters of the combined surface. Then， the surface topography parameters are connected in parallel with the fractal parameters by moment spectroscopy. The Chebyshev envelope function is introduced to calculate the surface morphology parameters interval under the influence of uncertainty. Finally， the uncertainty interval of surface morphology parameters is introduced into the statistical model to establish the contact stiffness model of joint surface considering the uncertainty of surface morphology parameters. The range of joint surface contact stiffness is obtained， and the influence of surface morphology parameters on the joint surface contact stiffness is explored. The results indicate that the model can accurately predict the range of changes in the surface contact stiffness of bolted connections， which can provide guidance for the design of the joint surface.

Key words: friction mechanics, uncertainty, joint surface, contact stiffness, surface topography parameters, Chebyshev envelope function

CLC Number: 

  • TH131.3

Fig.1

Sample and measurement location"

Table 1

Fractal parameter values under the samemeasured surface"

实验次数DG/10-7 mm
11.39086.6440
21.39718.5597
31.39219.1981
41.450323.635
51.472825.739
61.39176.9936
71.45258.9967
81.463540.223
91.507030.278
101.495951.1981

Fig.2

Surface contour height under different fractalparameters"

Fig.3

Interval influence of fractal parameters on surface topography parameters"

Table 2

Comparison table of comprehensive influenceof fractal parameters on joint surface parameters"

区间区间半径区间中点
［R］/μm［2.8028， 6.7898］2.05334.7963
［η］/μm -2［0.1378， 0.1649］0.013910.1514
［σs ］/μm［2.5352， 11.8701］4.80757.2027

Fig.4

Effect of contact gap on stiffness"

Fig.5

Influence of R on tangential contact stiffness"

Fig.6

Influence of η on tangential contact stiffness"

Fig.7

Influence of σs on tangential contact stiffness"

1 Burdekin M, Back N, Cowley A. Analysis of the local-deformations in machine joints[J]. ARCHIVE Journal of Mechanical Engineering Science, 1979, 21(1): 25-32.
2 杨成, 赵永胜, 刘志峰, 等.基于多尺度理论的栓接结合部动力学建模[J]. 吉林大学学报:工学版, 2019, 49(4): 1212-1220.
Yang Cheng, Zhao Yong-sheng, Liu Zhi-feng, et al. Stiffness model of bolted joint based on multi-scale theory[J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(4): 1212-1220.
3 廖静平, 张建富, 郁鼎文, 等. 基于虚拟梯度材料的螺栓结合面建模方法[J]. 吉林大学学报:工学版, 2016, 46(4): 1149-1155.
Liao Jing-ping, Zhang Jian-fu, Yu Ding-wen, et al. Modeling method of bolted joint interface based on gradient virtual materials[J]. Journal of Jilin University (Engineering and Technology Edition), 2016, 46(4): 1149-1155.
4 Ahmadian H, Mohsen M. A distributed mechanical joint contact model with slip/slap coupling effects[J]. Mechanical Systems and Signal Processing, 2016, 80: 206-223.
5 Brake M. The Mechanics of Jointed Structures: Recent Research and Open Challenges for Developing Predictive Models for Structural Dynamics[M]. Switzerland: Springer Nature, 2018.
6 Greenwood J A, Williamson J B P. Contact of nominally flat surfaces[J]. Proceedings of the Royal Society of London, 1966, 295(1442): 300-319.
7 Chang W R, Etsion I, Bogy D B. An elastic-plastic model for the contact of rough surfaces[J]. Asme J Trib, 1987, 109(2): 257-263.
8 Ciavarella M, Greenwood J A, Paggi M. Inclusion of "interaction" in the Greenwood and Williamson contact theory[J]. Wear, 2008, 265(5/6): 729-734.
9 Li Ling, Wang Jing⁃jing, Pei Xi⁃yong, et al. A modified elastic contact stiffness model considering the deformation of bulk substrate[J]. Journal of Mechanical Science and Technology, 2020, 34(10): 777-790.
10 Sayles R S, Thomas T R. Surface topography as a nonstationary random process[J]. Nature, 1978, 271(5644): 431-434.
11 Wang S, Komvopoulos K. A fractal theory of the interfacial temperature distribution in the slow sliding regime: part I—elastic contact and heat transfer analysis[J]. Journal of Tribology, 1994, 116(4): 812-822.
12 Wang S, Komvopoulos K. A fractal theory of the interfacial temperature distribution in the slow sliding regime: part II—multiple domains[J]. Journal of Tribology, 1994, 116(4): 824-832.
13 Yan W, Komvopoulos K. Contact analysis of elastic-plastic fractal surfaces[J]. Journal of Applied Physics, 1998, 84(7): 3617-3624.
14 Zhao Yong-sheng, Wu Hong-chao, Yang Cong-bin, et al. Interval estimation for contact stiffnes-s of bolted joint with uncertain parameters[J]. Advances in Mechanical Engineering, 2019, 11(11): 1-16.
15 Seibel A, Japing A, Schlattmann J. Uncertainty analysis of the coefficients of friction during the tightening process of bolted joints[J]. Journal of Uncertainty Analysis & Applications, 2014, 2(1): 1-11.
16 Langer P, Sepahvand K, Guist C, etal. Finite element modeling for structural dynamic analysis of bolted joints under uncertainty[J]. Procedia Engineering, 2017, 199: 954-959.
17 Dohnal F, Mace B R, Ferguson N S. Joint uncertainty propagation in linear structural dynamics using stochastic reduced basis methods[J]. AIAA Journal, 2009, 47(4): 961-969.
18 李坤, 曾劲, 于明月, 等. 考虑螺栓连接刚度不确定性的带法兰-圆柱壳结构频响函数分析[J]. 振动工程学报, 2020(3): 517-524.
Li Kun, Zeng Jin, Yu Ming-yue, et al. Analysis of frequency response function of flanged-cylinder shell structure considering the uncertainty of bolt connection stiffness[J]. Chinese Journal of Vibration Engineering, 2020(3): 517-524.
19 Li Hong-shuang, Gu Ru⁃jia, Zhao Xiang. Global sensitivity analysis of load distribution and displacement in multi-bolt composite joints. Composites[J]. Composites Part B, 2017, 116:200-210.
20 Majumdar A, Bhushan B. Fractal model of elastic-plastic contact between rough surfaces[J]. Tribol Trans ASME, 1991, 113(1): 1-11.
21 Xiao H, Sun Y. On the normal contact stiffness and contact resonance frequency of rough surface contact based on asperity micro-contact statistical models[J]. European Journal of Mechanics-A/Solids, 2019, 75: 450-460.
[1] Hai-bo LONG,Jia-qi YANG,Liang YIN,Xue-yu ZHAO,Zi-quan XIANG. Multi-objective decision-making on emergency material distribution under uncertain demand based on robust optimization [J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(4): 1078-1084.
[2] Dao WU,Li-bin ZHANG,Yun-xiang ZHANG,Hong-ying SHAN,Hong-mei SHAN. Visual detection method for vehicle braking time sequence based on slip rate identification [J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(1): 206-216.
[3] Gong CHENG,Ke XIAO,Jia-xu WANG,Wei PU,Yan-feng HAN. Gear contact stiffness under mixed lubrication status [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(2): 494-503.
[4] KOU Shu-qing, SHI Zhou. Three-dimensional reconstruction of fracture-split connecting rod joint surface and its strength and stiffness [J]. Journal of Jilin University(Engineering and Technology Edition), 2018, 48(5): 1515-1523.
[5] JIANG Lai-wei, SHA Xue-jun, WU Xuan-li, ZHANG Nai-tong. Novel joint user association and resource allocation method in LTE-A HetNets [J]. 吉林大学学报(工学版), 2017, 47(6): 1926-1932.
[6] JIANG Hai-yu, LIU Yu-hai, SUN Hai-lin, XU Ke-bin, BAI Tian-zeng, CHEN Zu-bin. Stratum undulation velocity model optimization algorithm for microseismic monitoring on surface [J]. 吉林大学学报(工学版), 2017, 47(6): 1969-1975.
[7] FENG Jian-xin. Recursive robust filtering for uncertain systems with delayed measurements [J]. 吉林大学学报(工学版), 2017, 47(5): 1561-1567.
[8] CHEN He, YANG Zhi-jun, WU Zhao-chun, Feng Zhi-gang, ZHAO Ke-jia, LI Di-fei, TIAN Di. Standard generator and its calibration method for analog component video signal with distortion [J]. 吉林大学学报(工学版), 2017, 47(4): 1159-1164.
[9] FENG Jian-xin, WANG Ting-feng, GUO Jin. Iterative robust filtering for uncertain systems with missing measurements [J]. 吉林大学学报(工学版), 2014, 44(4): 1057-1061.
[10] FU Shuang,LI Yi-bing,YE Fang,GAO Zhen-guo. Fast blind spectrum sensing using Sevcik fractal dimension in frequency domain [J]. 吉林大学学报(工学版), 2014, 44(3): 854-860.
[11] YANG Zhi-xiao, FAN Yan-feng, SUN Fu-yan. Uncertainty control based on normal cloud model for nodding actions of virtual human [J]. 吉林大学学报(工学版), 2012, 42(02): 476-482.
[12] JIAO De-yu. Robust trajectory tracking control of four-wheel mobile car [J]. 吉林大学学报(工学版), 2011, 41(增刊2): 301-305.
[13] SHAO Ji-ye,WANG Ri-xin,XU Min-qiang. Application of Bayesian network in model-based fault diagnosis [J]. 吉林大学学报(工学版), 2010, 40(01): 234-0237.
[14] WANG Xiao-bing,CHEN Jian-jun,CHEN Yong-qin,XIE Yong-qiang,CHEN Long . Robust control of uncertain piezothermoelasticity intelligent laminated plate with small interval parameters [J]. 吉林大学学报(工学版), 2009, 39(01): 182-187.
[15] WANG Xiao-li, ZHANG De-jun, ZHANG Shao-jie, YANG Yin-sheng . Study on Benefit Analysis and Calculation of Uncertain Anti-disaster Investment [J]. 吉林大学学报(工学版), 2002, (2): 22-27.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
Copyright © Journal of Jilin University(Engineering and Technology Edition), All Rights Reserved.
Tel: +86-431-85095297　Fax: +86-431-85094074　E-mail: xbgxb@jlu.edu.cn
Powered by Beijing Magtech Co. Ltd