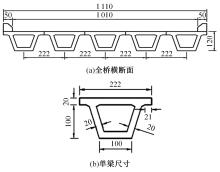
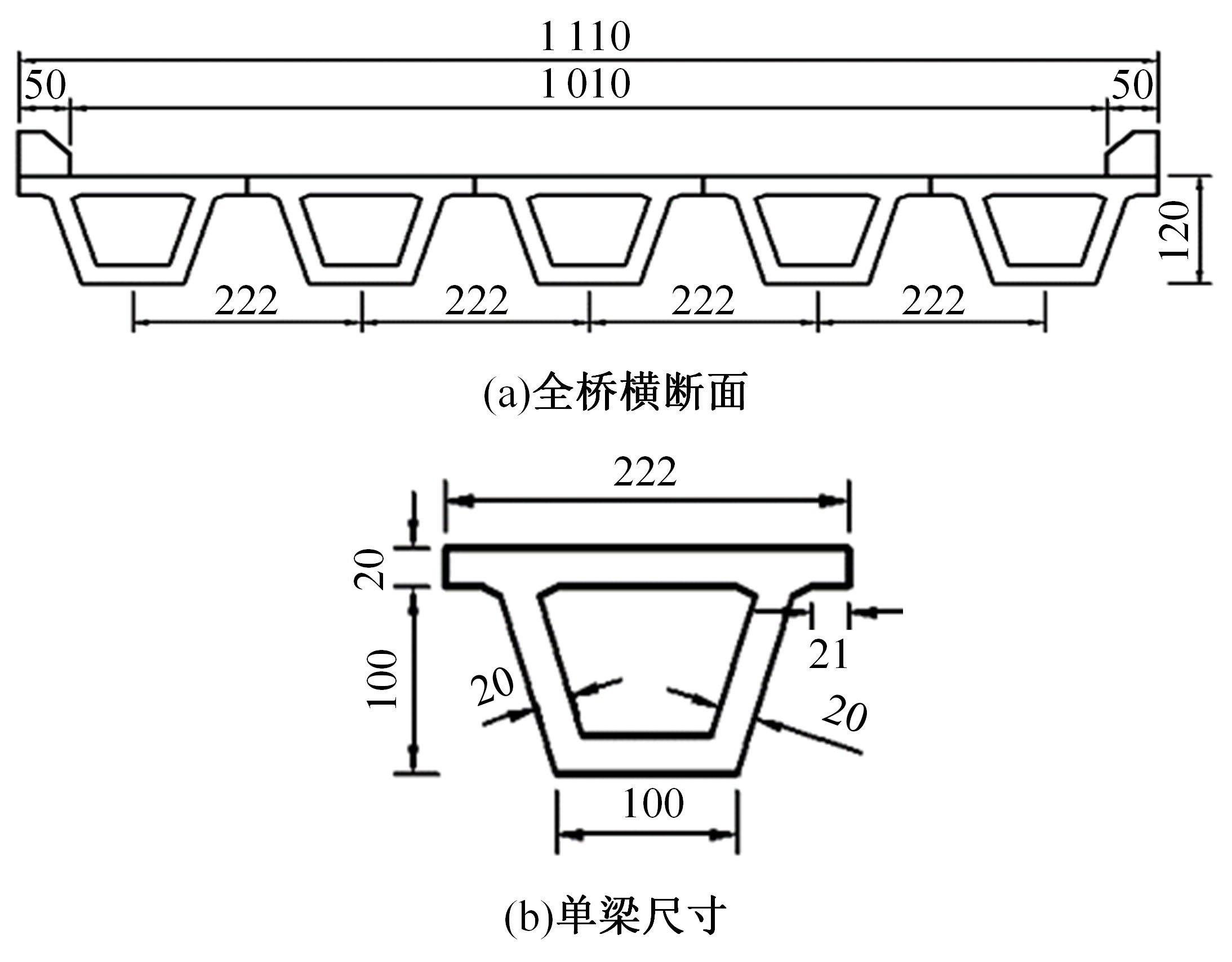
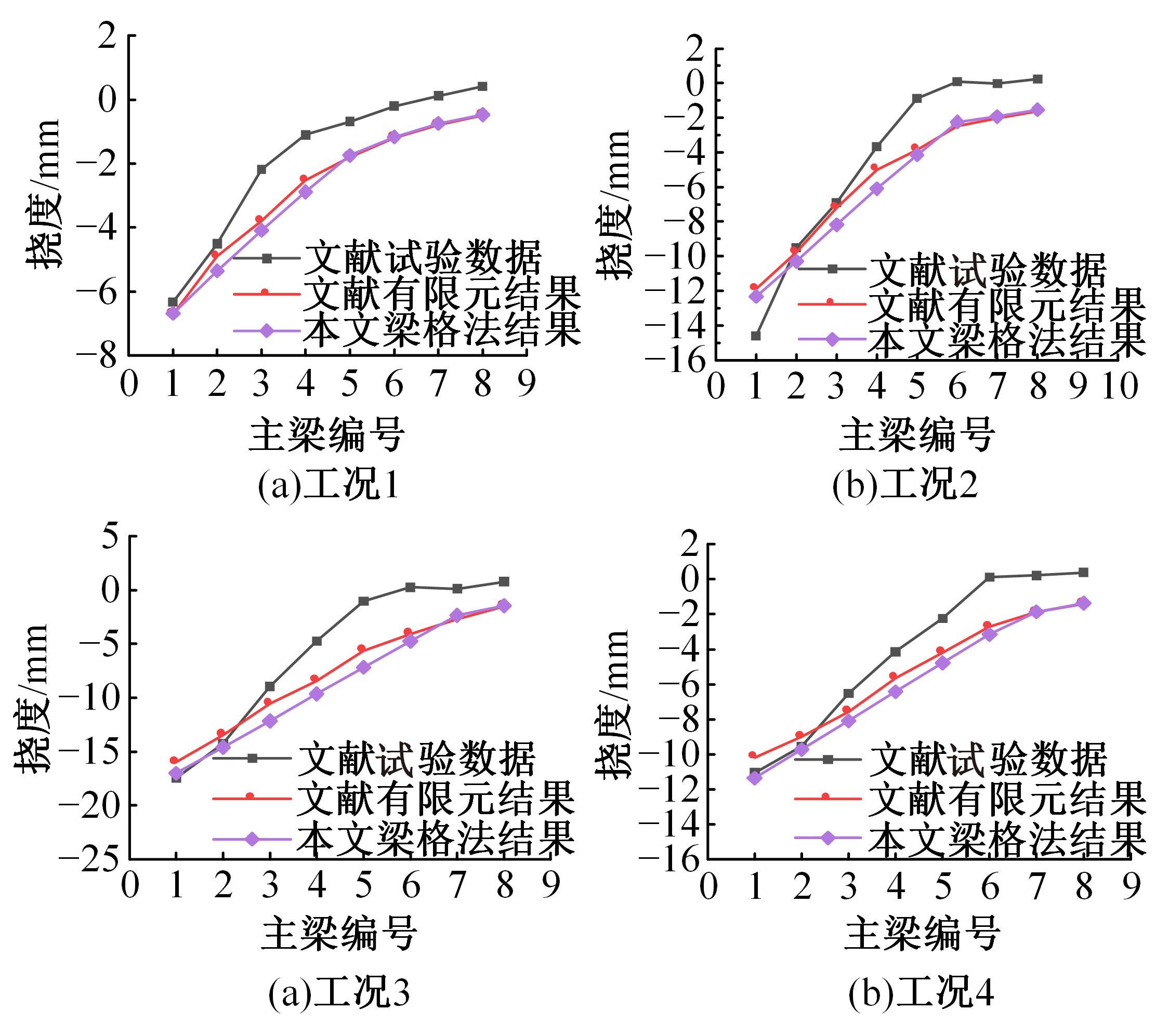
Journal of Jilin University(Engineering and Technology Edition) ›› 2024, Vol. 54 ›› Issue (6): 1688-1700.doi: 10.13229/j.cnki.jdxbgxb.20221079
Proposed formulae for transverse distribution factor of internal forces of prefabricated small box-girder bridge
Yan-ling ZHANG1,2( ), JIAYun-fei1,2,Xiao-yuan JIA1,2,Wang ZHENG1,2,Yun-sheng LI1,2(
), JIAYun-fei1,2,Xiao-yuan JIA1,2,Wang ZHENG1,2,Yun-sheng LI1,2( )
)
- 1.School of Civil Engineering,Shijiazhuang Tiedao University,Shijiazhuang 050043,China
2.Key Laboratory of Roads and Railway Engineering Safety Control of Ministry of Education,Shijiazhuang Tiedao University,Shijiazhuang 050043,China
CLC Number:
- U448.25
| 1 | American Association of State Highway & Transportation Officials. AASHTO LRFD bridge design specifications[EB/OL].[2022-08-15]. |
| 2 | Bernardi P, Cerioni R, Leurini F, et al. A design method for the prediction of load distribution in hollow-core floors[J]. Engineering Structures, 2016, 123: 473-481. |
| 3 | Zhao Y, Cao X Z, Zhou Y J, et al. Lateral load distribution for hollow slab bridge: field test investigation [J]. International Journal of Concrete Structures and Materials, 2020, 14:No. 22. |
| 4 | 战家旺, 高胜星, 闫宇智,等. 基于模型修正的公路简支板梁桥荷载横向分布系数计算方法[J]. 中国公路学报, 2019, 32(5): 72-79. |
| Zhan Jia-wang, Gao Sheng-xing, Yan Yu-zhi, et al.A calculation method for transverse load distribution coefficient of highway simply-supported slab-girder bridges based on model updating[J]. China J Highw Transp, 2019,32(5): 72-79. | |
| 5 | 王渠, 吴庆雄, 陈康明, 等. 拼宽空心板桥荷载横向分布计算方法[J]. 中国公路学报, 2019, 32(7): 57-65. |
| Wang Qu, Wu Qing-xiong, Chen Kang-ming, et al. Calculation method of load transverse-distribution for widening hollow slab bridge[J]. China J Highw Transp, 2019,32(7): 57-65. | |
| 6 | Tevfik T, Mary B D H, John B M. Live load distribution factors for spread slab beam bridges[J]. J Bridge Eng, 2017, 22(10): No. 04017067. |
| 7 | 邬晓光, 魏俊杰. 宽幅装配式箱梁桥荷载横向分布系数计算[J]. 沈阳建筑大学学报:自然科学版, 2020, 36(1): 76-85. |
| Wu Xiao-guang, Wei Jun-jie. Calculation of load transverse distribution coefficient of wide assembled box girder bridge[J]. Journal of Shenyang Jianzhu University (Natural Science), 2020,36(1): 76-85. | |
| 8 | 何伟南, 周怀治, 王银辉. 多室宽箱梁桥横向分布计算的刚接梁法[J]. 公路交通科技:应用技术版, 2016, 12(1): 212-216. |
| He Wei-nan, Zhou Huai-zhi, Wang Yin-hui. Rigid-jointed girder method for transverse distribution calculating of wide multi-cell box girder bridges[J]. Journal of Highway and Transportation Research and Development (Application Technology Edition), 2016,12(1): 212-216. | |
| 9 | 闫林君, 张经伟, 罗奎. 装配式多主梁钢-混组合梁桥的荷载横向分布研究[J]. 公路交通科技, 2020, 37(3): 59-69. |
| Yan Lin-jun, Zhang Jing-wei, Luo Kui. Study on lateral load distribution of prefabricated multi-girder steel-concrete composite girder bridge[J]. Journal of Highway and Transportation Research and Development, 2020, 37(3): 59-69. | |
| 10 | Kong S Y, Zhuang L D, Tao M X, et al. Load distribution factor for moment of composite bridges with multi-box girders[J]. Engineering Structures, 2020, 215(10): No. 110716. |
| 11 | Ma L, Zhou L Y, Wan S. Study of the calculation method of lateral load distribution on a continuous composite box girder bridge with corrugated steel webs[J]. Journal of Highway and Transportation Research and Development, 2014, 8(2): 42-46. |
| 12 | 聂鑫, 樊健生, 付裕. 箱形截面连续组合梁桥的荷载横向分布[J]. 清华大学学报:自然科学版, 2009, 49(12): 1930-1933, 1938. |
| Nie Xin, Fan Jian-sheng, Fu Yu. Transverse load distribution on box section continuous composite steel-concrete bridges[J]. Journal of Tsinghua University (Sci&Tech), 2009,49(12): 1930-1933, 1938. | |
| 13 | 余泉. 多箱式连续小箱梁桥受力特性的分析及其试验研究[D]. 杭州: 浙江大学建筑工程学院, 2006. |
| Yu Quan. Analysis of structure behavior of continuous multi-box girder bridges and its experimental study[D]. Hangzhou: College of Civil Engineering and Architecture, Zhejiang University, 2006. | |
| 14 | Huang H X, Shenton H W. Chajes M J. Load distribution for a highly skewed bridge: testing and analysis[J]. J Bridge Eng, 2004, 9(6): 558-562. |
| 15 | Fatemi S J, Mohamed Ali M S, Sheikh A H. Load distribution for composite steel-concrete horizontally curved box girder bridge[J]. Journal of Constructional Steel Research, 2016, 116: 19-28. |
| 16 | 魏志刚, 刘寒冰, 时成林, 等. 考虑桥面铺装作用的简支梁桥横向分布系数计算[J]. 吉林大学学报:工学版, 2018, 48(1): 105-112. |
| Wei Zhi-gang, Liu Han-bing, Shi Cheng-lin, et al. Calculation of transverse distribution coefficient of simply supported beam bridge with effect of bridge deck pavement[J]. Journal of Jilin University (Engineering and Technology Edition), 2018, 48(1): 105-112. | |
| 17 | 张学龙. 小箱梁的梁格划分及虚拟横梁刚度分析研究[D]. 西安: 长安大学公路学院, 2013. |
| Zhang Xue-long. Study and analysis on beam meshing and the virtual beam stiffness of Small box girder [D]. Xi'an: School of Highway, Chang'an University, 2013. | |
| 18 | 管路, 贾鹏, 向天华,等. 组合小箱梁横向分布系数影响因素分析研究[J]. 福建建材, 2020(6): 10-13. |
| Guan Lu, Jia Peng, Xiang Tian-hua, et al. Analysis of the influencing factors on the transverse distribution factor of the composite small box girder[J]. Fujian Building Materials, 2020(6): 10-13. |
| [1] | Yan-ling ZHANG,Can WANG,Xu ZHANG,Ang-yang WANG,Yun-sheng LI. Human⁃induced vibration analysis and pedestrian comfort evaluation for suspension footbridge with different hunger systems [J]. Journal of Jilin University(Engineering and Technology Edition), 2022, 52(11): 2644-2652. |
| [2] | Chang-jun ZHONG,Zhong-bin WANG,Chen-yang LIU. Influencing factors and structural optimization of main cable saddle bearing capacity of suspension bridge [J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(6): 2068-2078. |
| [3] | Lun-hua BAI,Rui-li SHEN,Xing-biao ZHANG,Lu WANG. In-plane stability of self-anchored suspension bridge [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(5): 1500-1508. |
|
||