自锚式悬索桥的面内稳定性

doi:10.13229/j.cnki.jdxbgxb20180178

Abstract

Abstract:

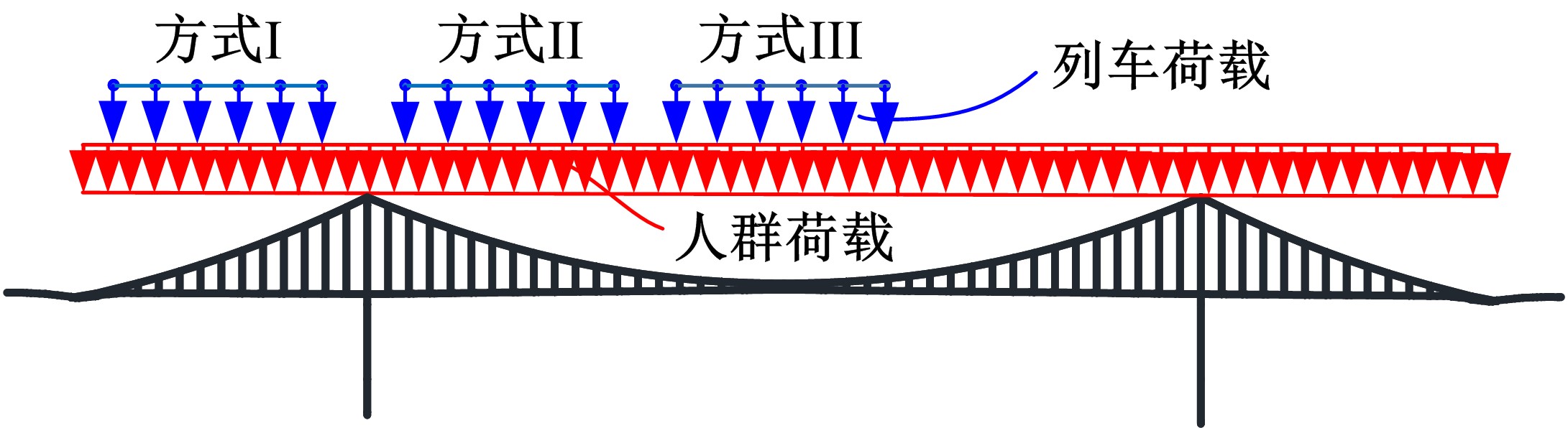
In order to consummate the in-plane stability theory of self-anchored suspension bridge, firstly it is preliminarily determined that the bifurcation failure mode of this type bridge can not occur through the concept of structural stability. Furthermore, by introducing the displacement interference which is assumed as power series form in the deflection equation of the self-anchored suspension bridge, it is proved that the elastic bifurcation instability will not occur. Finally, a practical bridge is taken as an example, the numerical models according to the elastic stability and elastic-plastic stability theory are calculated and analyzed to obtain the load coefficient, bridge failure modes etc.. The results show that there is no in-plane bifurcation failure mode for self-anchored suspension bridge in the scope of application of deflection theory. Numerical analysis shows that the bifurcation instability in the actual bridge deck is caused by the breakage of the sling, which exceeds the application range of deflection theory, and the ultimate bearing capacity satisfies the safety requirements.

Key words: bridge engineering, self-anchored suspension bridge stability theory, numerical analysis method, cable-sling-girder closed transmission path, deflection theory, bifurcation instability

CLC Number:

U448.25

Lun-hua BAI,Rui-li SHEN,Xing-biao ZHANG,Lu WANG. In-plane stability of self-anchored suspension bridge[J].Journal of Jilin University(Engineering and Technology Edition), 2019, 49(5): 1500-1508.

Figures/Tables 14

Fig.1

Fig.2

Fig.3

Fig.4

Fig.5

Fig.6

Fig.7

Fig.8

Table 1

Fig.9

Fig.10

Fig.11

Table 2

Fig.12

References 15

1	Nie Jian-guo , Zhou Meng , Wang Yu-hang , et al . Cable anchorage system modeling methods for self-anchored suspension bridges with steel box girders[J]. Journal of Bridge Engineering, 2014, 19(2): 172-185.
2	王邵锐, 周志祥, 高燕梅, 等 . 考虑缆-梁联合作用的自锚式悬索桥恒载状态计算方法研究［J］. 土木工程学报, 2015, 48(8): 70-76.
	Wang Shao-rui , Zhou Zhi-xiang , Gao Yan-mei , et al . Study on the calculation method of the dead load state for the self-anchored suspension bridge considering the joint action of cable-stiffening girder[J]. China Civil Engineering Journal, 2015, 48(8): 70-76.
3	李建慧, 李爱群 . 自锚式悬索桥静力随机分析与可靠度评估［J］. 中国公路学报, 2012, 25(6): 74-79.
	Li Jian-hui , Li Ai-qun . Stochastic analysis of static charateristics and reliability assessment for self-anchored suspension bridge[J]. China Journal of Highway and Transport, 2012, 25(6): 74-79.
4	王保群, 张强勇, 张凯, 等 . 自锚式斜拉-悬吊协作体系桥梁动力性能［J］. 吉林大学学报: 工学版, 2009, 39(3): 686-690.
	Wang Bao-qun , Zhang Qiang-yong , Zhang Kai , et al . Dynamic characteristics for self-anchored cable-stayed suspension bridges[J]. Journal of Jilin University (Engineering and Technology Edition), 2009, 39(3): 686-690.
5	沈锐利, 齐东春, 唐茂林 . 杭州江东大桥静力特性全桥模型试验研究［J］. 土木工程学报, 2011, 44(1): 74-80.
	Shen Rui-li , Qi Dong-chun , Tang Mao-lin . Model test study of the static property of the Jiangdong Bridge in Hangzhou[J]. China Civil Engineering Journal, 2011, 44(1): 74-80.
6	胡建华, 沈锐利, 张贵明, 等 . 佛山平胜大桥全桥模型试验研究[J]. 土木工程学报, 2007, 40(5): 17-25.
	Hu Jian-hua , Shen Rui-li , Zhang Gui-ming , et al . Total bridge model study of the Pingsheng Bridge in Foshan[J]. China Civil Engineering Journal, 2007, 40(5): 17-25.
7	王桢, 吴海军, 周志祥, 等 . 大跨径自锚式悬索桥吊索索力相邻影响分析［J］. 土木工程学报, 2016, 49(6): 51-60.
	Wang Zhen , Wu Hai-jun , Zhou Zhi-xiang , et al . Analysis on near influence of cable force in large-span self-anchored suspension bridges[J]. China Civil Engineering Journal, 2016, 49(6): 51-60.
8	胡建华, 王连华, 沈锐利, 等 . 大跨度自锚式悬索桥稳定性研究［J］. 湖南大学学报：自然科学版, 2008, 35(7): 12-15.
	Hu Jian-Hua , Wang Lian-hua , Shen Rui-li , et al . Research on the stability of long span self-anchored suspension bridges[J]. Journal of Hunan University (Natural Sciences), 2008, 35(7): 12-15.
9	Jung M R , Shin S U , Attard M M , et al . Deflection theory for self-anchored suspension bridges under live load[J]. Journal of Bridge Engineering, 2014, 20(7): 1-19.
10	Jung M R , Jang M J , Attard M M , et al . Elastic stability behavior of self-anchored suspension bridges by the deflection theory[J]. International Journal of Structural Stability & Dynamics, 2017, 17(4): 1-23.
11	李立峰, 程翔云 . 代换梁法在自锚式悬索桥上的推广应用［J］. 工程力学, 2008, 25(8): 212-217.
	Li Li-feng , Cheng Xiang-yun . Extensional application of substitutional beam method to self-anchored suspension bridge[J]. Engineering Mechanics, 2008, 25(8): 212-217.
12	赵维贺 . 新型自锚式悬索桥的稳定性及极限承载力分析［D］. 大连：大连理工大学土木工程学院, 2007.
	Zhao Wei-he . The buckle and ultimate bearing capacity analysis for a new style self-anchored suspension bridge[D]. Dalian: School of Civil Engieering, Dalian University of Technology, 2007.
13	铁道第三勘察设计院 . 铁路桥涵设计基本规范［M］. 2版. 北京：中国铁道出版社, 2005.
14	重庆交通科研设计院 . 公路斜拉桥设计细则(JTG/T D65-01-2007)［M］. 北京：人民交通出版社， 2007.
15	沈锐利, 成新, 白伦华, 等 . 自锚式悬索桥极限承载力及安全性评价方法研究［J］. 铁道学报, 2017, 39(11): 89-96.
	Shen Rui-li , Cheng Xin , Bai Lun-hua , et al . Study on static ultimate bearing capacity and safety evaluation method of self-anchored suspension bridges[J]. Journal of the China Railway Society, 2017， 39(11): 89-96.

Related Articles 15

[1]	Shi⁃cheng WAN,Qiao HUANG,Jian GUAN,Zhao⁃yuan GUO. Strengthening of continuous steel⁃concrete composite beams in negative moment region using prestressed carbon fiber⁃reinforced polymer plates [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(4): 1114-1123.
[2]	Jin⁃gang ZHAO,Ming ZHANG,Yu⁃lin ZHAN,Ming⁃zhi XIE. Damage criterion of reinforced concrete pier based on plastic strain energy density [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(4): 1124-1133.
[3]	Wan⁃heng LI,Lin SHEN,Shao⁃peng WANG,Shang⁃chuan ZHAO. Damage assessment of bridge construction based onmulti⁃stage subregion mobile test [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(3): 773-780.
[4]	HUI Ying-xin,MAO Ming-jie,LIU Hai-feng,ZHANG Shang-rong. Influence of structural seismic response of bridges crossing active fault [J]. Journal of Jilin University(Engineering and Technology Edition), 2018, 48(6): 1725-1734.
[5]	ZHENG Yi-feng, ZHAO Qun, BAO Wei, LI Zhuang, YU Xiao-fei. Wind resistance performance of long-span continuous rigid-frame bridge in cantilever construction stage [J]. 吉林大学学报(工学版), 2018, 48(2): 466-472.
[6]	GONG Ya-feng, HE Yu-long, TAN Guo-jin, SHEN Yang-fan. Anti-overturning stability analysis for three-span continuous curved girder bridge with single column pier [J]. 吉林大学学报(工学版), 2018, 48(1): 133-140.
[7]	WEI Zhi-gang, LIU Han-bing, SHI Cheng-lin, GONG Ya-feng. Calculation of transverse distribution coefficient of simply supported beam bridge with effect of bridge deck pavement [J]. 吉林大学学报(工学版), 2018, 48(1): 105-112.
[8]	WEI Zhi-gang, SHI Cheng-lin, LIU Han-bing, ZHANG Yun-long. Dynamic characteristics of steel-concrete composite simply supported beam under vehicles [J]. 吉林大学学报(工学版), 2017, 47(6): 1744-1752.
[9]	ZHANG Yun-long, LIU Zhan-ying, WU Chun-li, WANG Jing. Static and dynamic responses of steel-concrete composite beams [J]. 吉林大学学报(工学版), 2017, 47(3): 789-795.
[10]	LIU Han-bing, SHI Cheng-lin, TAN Guo-jin. Finite element solution of composite beam with effect of shear slip [J]. 吉林大学学报(工学版), 2016, 46(3): 792-797.
[11]	TAN Guo-jin, LIU Zi-yu, WEI Hai-bin, WANG Long-lin. Calculation of natural frequency of simply supported beam bridge reinforced with eccentric prestressed tendons [J]. 吉林大学学报(工学版), 2016, 46(3): 798-803.
[12]	CAO Shan-shan, LEI Jun-qing. Fatigue life prediction of steel structure considering interval uncertainty [J]. 吉林大学学报(工学版), 2016, 46(3): 804-810.
[13]	XIAO Yun, LEI Jun-qing, ZHANG Kun, LI Zhong-san. Fatigue stiffness degradation of prestressed concrete beam under multilevel amplitude cycle loading [J]. 吉林大学学报(工学版), 2013, 43(03): 665-670.
[14]	JIAO Chang-ke, LI Ai-qun, WU Xiao-ping. Double-deck long-span cable-stayed bridge seismic response to multi-support excitation [J]. , 2012, 42(04): 910-917.
[15]	LIU Han-bing, ZHENG Ji-guang, ZOU Pin-de. Calculation on bearing capacity of eccentric compression reinforced concrete short column with circular combined-section [J]. 吉林大学学报(工学版), 2011, 41(增刊2): 159-163.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

Comments

Recommended 0

No Suggested Reading articles found!

工况号	列车布载方式	桥塔效应
1	1	不考虑
2	2	不考虑
3	3	不考虑
4	1	考虑
5	2	考虑
6	3	考虑

工况号	活载布载方式	荷载模式	最大荷载倍数
7	截面①轴力最不利	活载单独放大	10.08
8	截面①正弯矩最不利		11.79
9	截面②轴力最不利		10.14
10	截面②负弯矩最不利		9.01
11	截面③轴力最不利		10.13
12	截面③正弯矩最不利		10.02
7a	截面①轴力最不利	恒载活载同比放大	2.21
8a	截面①正弯矩最不利		2.17
9a	截面②轴力最不利		2.21
10a	截面②负弯矩最不利		1.98
11a	截面③轴力最不利		2.27
12a	截面③正弯矩最不利		2.59

In-plane stability of self-anchored suspension bridge

RICH HTML

PDF (PC)