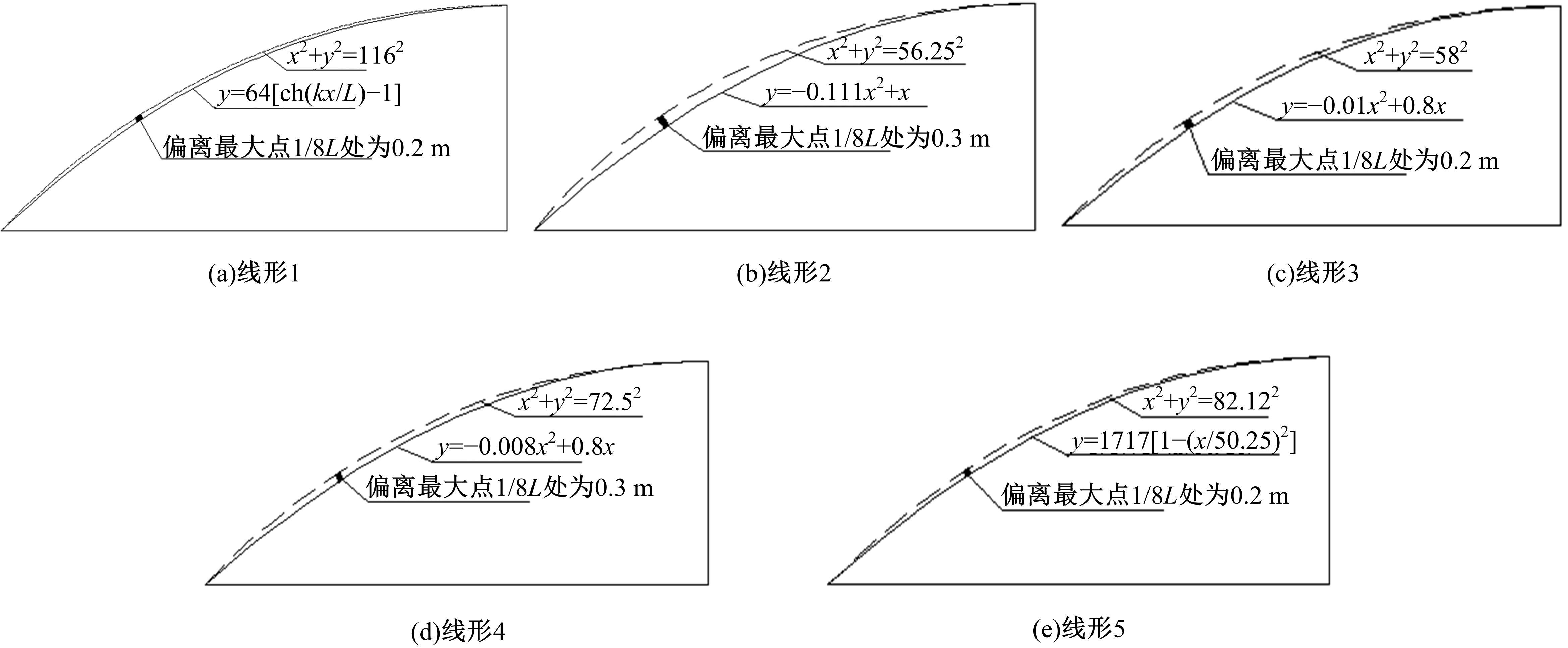
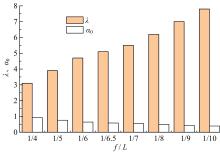
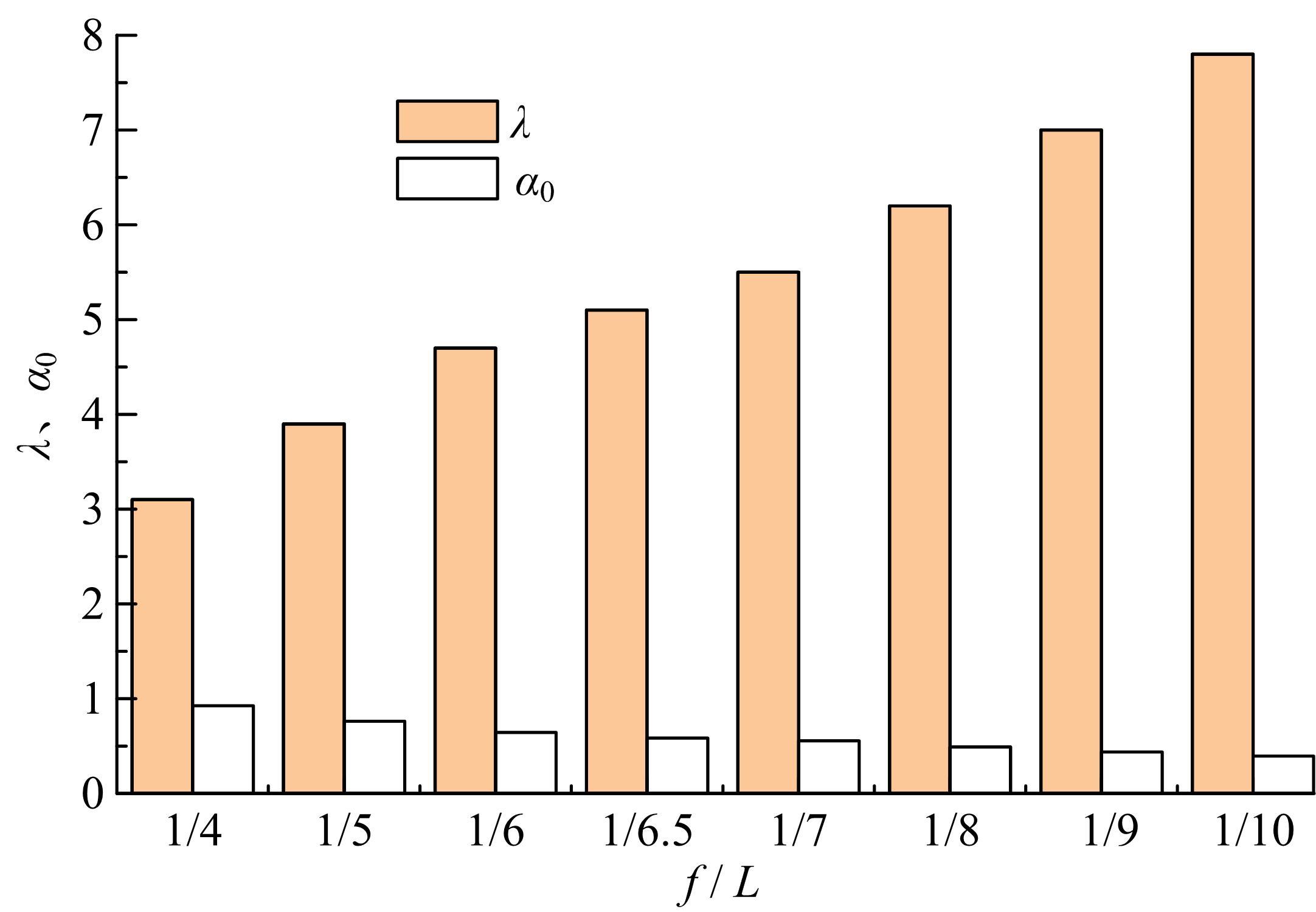
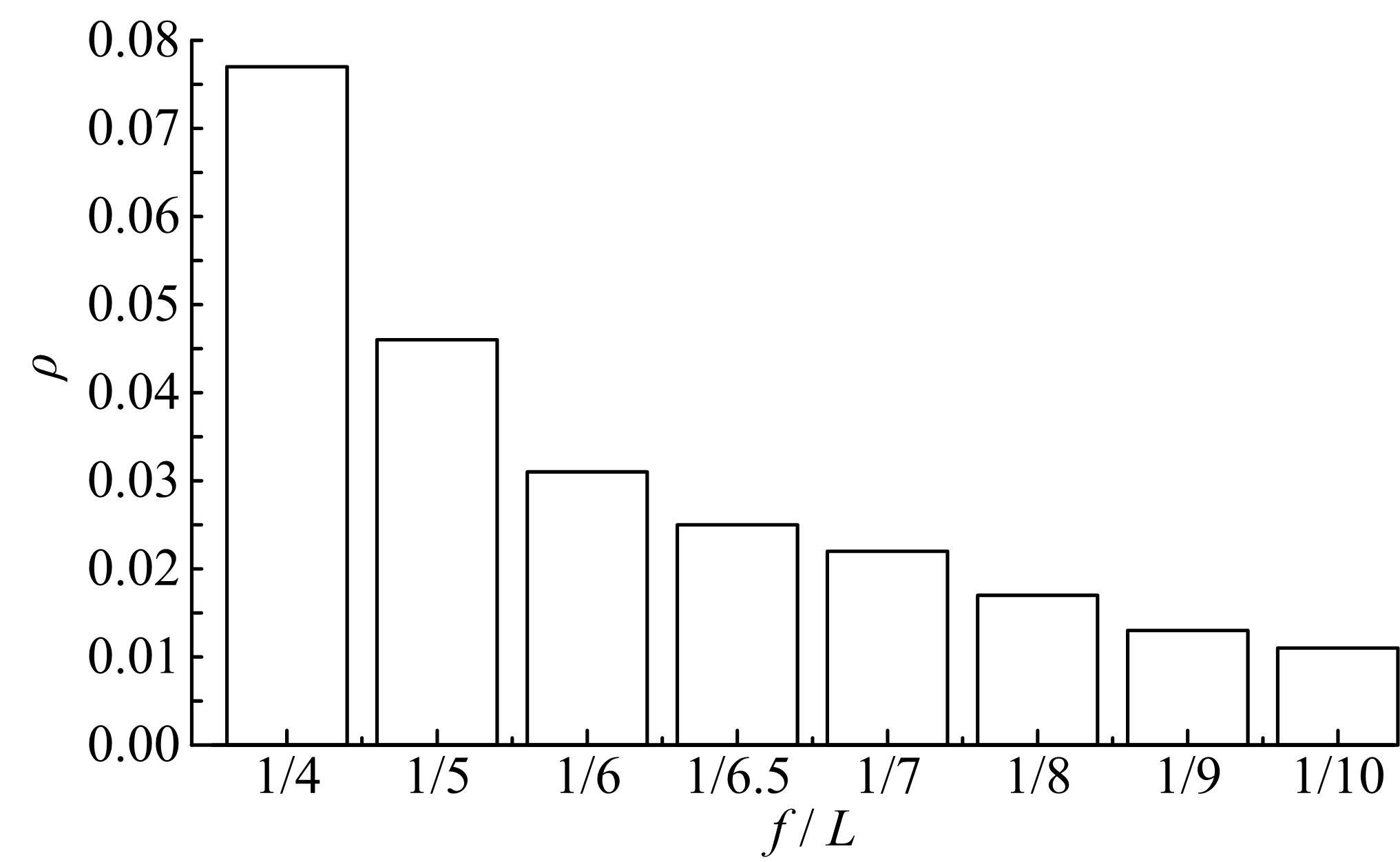
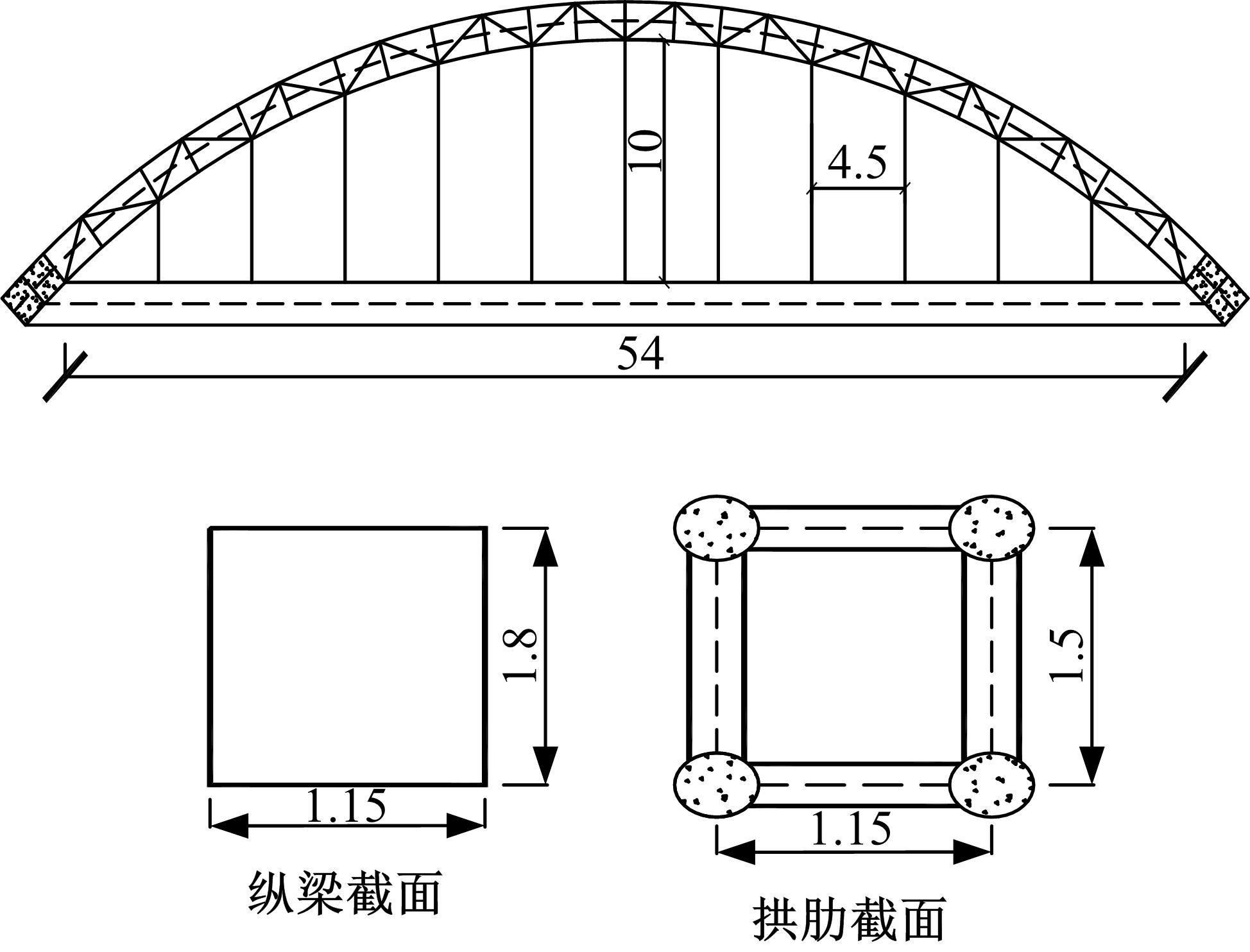
Journal of Jilin University(Engineering and Technology Edition) ›› 2022, Vol. 52 ›› Issue (6): 1404-1412.doi: 10.13229/j.cnki.jdxbgxb20220147

Previous Articles    

Calculation method of eccentricity increase coefficient of arch rib of long⁃span arch bridge

Feng GUO1,2(),Peng-fei LI3(),Jia-yan MAO4,Yan-zhao DONG4   

  1. 1.School of Civil Engineering，Shijiazhuang Tiedao University，Shijiazhuang 050043，China
    2.Key Laboratory of Roads and Railway Engineering Safety Control，Ministry of Education，Shijiazhuang Tiedao University，Shijiazhuang 050043，China
    3.Key Laboratory of Transportation Industry of Old Bridge Inspection and Reinforcement Technology （Beijing），Beijing 100085，China
    4.Shijiazhuang Rail Transportation Group Co. ，Ltd. ，Shijiazhuang 050035，China
  • Received:2022-01-30 Online:2022-06-01 Published:2022-06-02
  • Contact: Peng-fei LI E-mail:guofeng2013@126.com;pf.li@rioh.cn

RICH HTML

 4   

PDF (PC)

256

Abstract:

Combined with the basic principle of variational method and the characteristics of interaction after deformation of tied arch structure， a practical calculation method of eccentric distance increase coefficient is proposed. Through engineering case analysis， the calculation result of this paper is compared with the normative method of bridge and the finite element method. The results show that the calculation formula specified in the code has the largest result， the calculation result of the formula is large， the finite element calculation result is small. This above means the proposed method is widely applicable and safe. The calculations of the eccentricity increase coefficient of are quite different in catenary， parabola， circular arc and straight rod with constraints at both ends， related to the constraint conditions of the tie-rod arch and the forms of load.

Key words: variational method, moment amplification coefficient, strain potential energy, second-order moment effect, arch rib

CLC Number: 

  • TU318

Fig.1

Symbolic provisions of arch ring"

Table 1

Comparison of three linear parameters of parabola， catenary and circular arc"

桥名偏离图示跨径/m矢跨比拱肋线形拱截面高度/m与圆弧线偏离值/m弧度长度偏离值/m
拱肋1I1601/5.1三次抛物线3.80.152.01
拱肋2II901/4.8悬链线2.00.271.90
拱肋3III801/4.7悬链线1.40.181.11
拱肋4IV1001/5.1三次抛物线2.60.191.21
拱肋5V100.51/5.75三次抛物线2.70.211.01

Fig.2

Comparison diagram of catenary， parabola and circular arc after equivalence"

Fig.3

Diagram of deformed arch structure"

Fig.4

Comparison of λ、α0 values"

Fig.5

Comparison of ρ value"

Fig.6

Dimension drawing of arch structure（unit：m）"

Fig.7

Calculation model of tied arch"

Table 2

Internal force distribution of arch ribin key section under elastic and geometric nonlinearity"

关键截面位置轴向压力值/kN弹性弯矩值/（kN·m）几何非线性弯矩值/（kN·m）
1/2L6501.21641.6541292.598
1/4L9104.71731.4501210.842

Table 3

Calculation results of eccentricity increase coefficient"

参数关键截面位置参数关键截面位置
L/2L/4L/2L/4
系杆截面刚度/（N·m-1）0.570.57K1.101.10
拱肋截面刚度/（N·m-1）0.330.33P0.050.05
化解为圆弧后半径R/m42.2842.28η11.431.60
拱肋弧线长度S/m64.3564.35η21.441.61
截面偏心距e0/m0.260.20η31.891.89
圆心角值α/（°）0.220.22η41.301.50

Table 4

Eccentricity increasing coefficient comparison of this paper with other algorithms"

关键截面位置η1-η2η2/%η1-η3η3/%η1-η4η4/%
L/20.7124.6610.35
L/41.3215.949.24

Fig.8

Comparison of calculation results of differentformulas at key sections"

1 黄侨, 黄义理, 郑清刚, 等. 常泰长江大桥塔柱偏心距增大系数的计算方法[J].长安大学学报: 自然科学版, 2021, 41(3): 42-51.
Huang Qiao, Huang Yi-li, Zheng Qing-gang, et al. Calculation methods of pylon eccentricity magnified coefficient of Changtai Yangtze River Bridge[J]. Journal of Chang'an University(Natural Science Edition), 2021, 41(3): 42-51.
2 李春阳. 复杂边界下柔性高墩的受力性能研究[D]. 长沙:湖南大学土木工程学院, 2018.
Li Chun-yang. The research on mechanical behavior of flexible high-piers with complex boundary conditions[D]. Changsha: School of Civil Engineering, Hunan University, 2018.
3 . 公路钢筋混凝土及预应力混凝土桥涵设计规范 [S].
4 Wang Qiu-wei, Shi Qing-xuan, Jiang Wei-shan. The second-order effect of src columns under eccentric compression[J]. Mechanics in Engineering, 2011, 33(3): 34-37, 41.
5 王浩然, 许晶. 钢筋混凝土结构的二阶效应分析方法[C]∥北京力学会第二十四届学术年会, 中国, 北京, 2018: 946-948.
Wang Hao-ran, Xu Jing. Second order effect analysis method of reinforced concrete structures[C]∥Proceedings of the 24th Annual Academic Conference of Beijing Society of Mechanics, Beijing, China, 2018: 946-948.
6 苑仁安, 傅战工, 郑清刚, 等. 超高桥塔结构偏心距增大系数计算方法[J]. 桥梁建设, 2021, 51(5): 37-43.
Yuan Ren-an, Fu Zhan-gong, Zheng Qing-gang, et al. Calculation method of eccentricity increasing coefficient of super high bridge tower structure[J]. Bridge Construction, 2021, 51 (5): 37-43.
7 李志渊, 陈全红. 钢筋砼长柱偏心距增大系数计算方法比较[J]. 兰州交通大学学报:自然科学版, 2007, 26(4): 66-69.
Li Zhi-yuan, Chen Quan-hong. Comparative study on the calculation method for eccentricity accreting factor of reinforced concrete slender columns[J] Journal of Lanzhou Jiaotong University(Natural Science), 2007, 26(4): 66-69.
8 徐田. FRP约束钢筋混凝土柱的承载性能研究[D]. 哈尔滨:哈尔滨工业大学土木工程学院, 2007.
Xu Tian. Research on bearing capacity of FRP confined reinforced concrete columns[D]. Harbin: School of Civil Engineering, Harbin Institute of Technology, 2007
9 Yun Y W, Liu X H, Kim S K, et al. Research on eccentricity magnification factor of eccentric compression lightweight aggregate concrete member[J]. Advanced Materials Research, 2011, 152-153: 717-721.
10 Rahman M E, Ting T Z H, Lau H H, et al. Behaviour of lightweight concrete wall panel under axial loading: experimental and numerical investigation toward sustainability in construction industry[J]. Buildings, 2021, 11(12): 620.
11 Robinson G P, Palmeri A, Austin S A. Design methodologies for one way spanning eccentrically loaded minimally or centrally reinforced pre-cast RC panels[J]. Engineering Structures, 2013, 56: 1945-1956.
12 Ting T Z H, Rahman M E, Lau H H, et al. Recent development and perspective of lightweight aggregates based self-compacting concrete[J]. Construction and Building Materials, 2019, 201: 763-777.
13 Ho N M, Doh J H. Prediction of ultimate strength of concrete walls restrained on three sides[J]. Structural Concrete, 2019, 20(3): 942-954.
[1] Jun ZHANG,Cheng QIAN,Chun⁃yan GUO,Yu⁃jun QIAN. Dynamic design of building livability based on multi⁃source spatiotemporal data [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(4): 1169-1173.
[2] NI Ying-sheng,SUN Qi-xin,MA Ye,XU Dong,LIU Chao. Shear distribution of multi-cell corrugated steel web composite beams based on space grid analysis [J]. Journal of Jilin University(Engineering and Technology Edition), 2018, 48(6): 1735-1746.
[3] NI Ying-sheng, SUN Qi-xin, MA Ye, XU Dong. Calculation of capacity reinforcement about composite box girder with corrugated steel webs based on tensile stress region theory [J]. 吉林大学学报(工学版), 2018, 48(1): 148-158.
[4] NI Ying-sheng, MA Ye, XU Dong, LI Jin-kai. Space mesh analysis method for shear lag effect of cable-stayed bridge with corrugated steel webs [J]. 吉林大学学报(工学版), 2017, 47(5): 1453-1464.
[5] XIAO Xiang, HUANG En-hou, NI Ying-sheng. Theoretical analysis and experiment of the effect of flange width on beam-plates system of prestressed concrete [J]. 吉林大学学报(工学版), 2015, 45(6): 1784-1790.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
Copyright © Journal of Jilin University(Engineering and Technology Edition), All Rights Reserved.
Tel: +86-431-85095297　Fax: +86-431-85094074　E-mail: xbgxb@jlu.edu.cn
Powered by Beijing Magtech Co. Ltd