Journal of Jilin University(Engineering and Technology Edition) ›› 2019, Vol. 49 ›› Issue (3): 749-756.doi: 10.13229/j.cnki.jdxbgxb20180120

Previous Articles     Next Articles

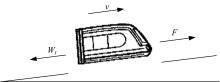
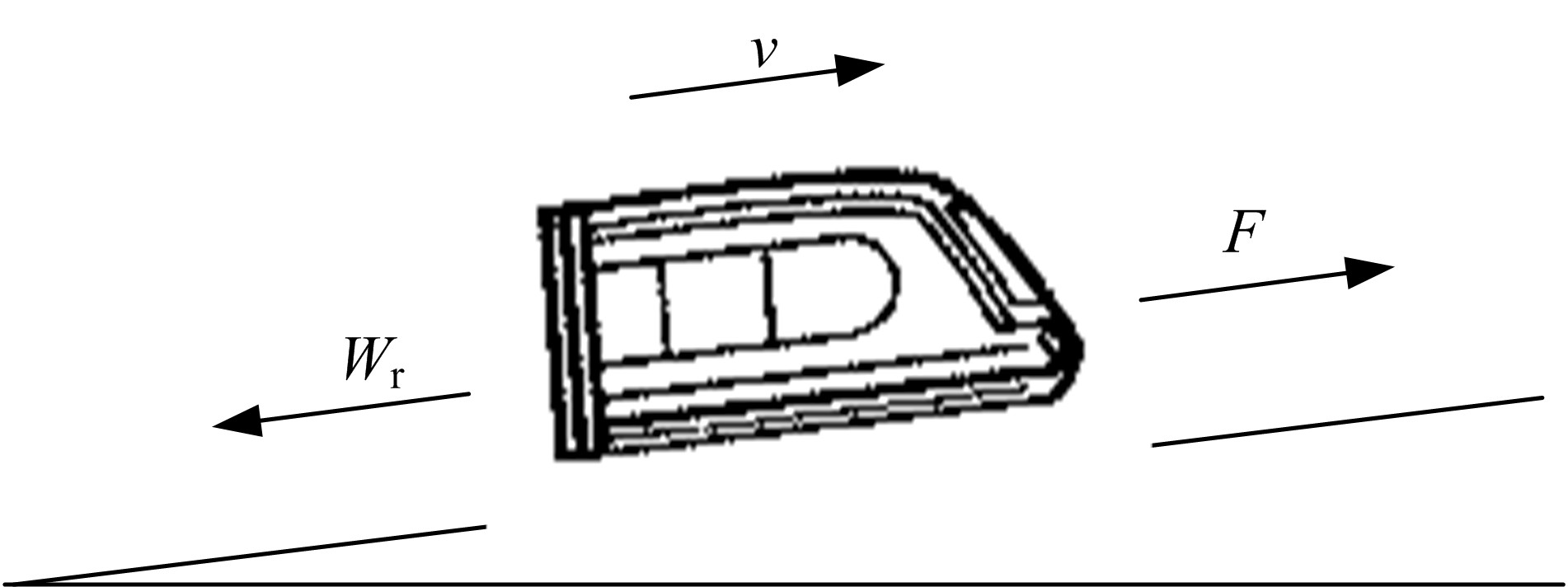
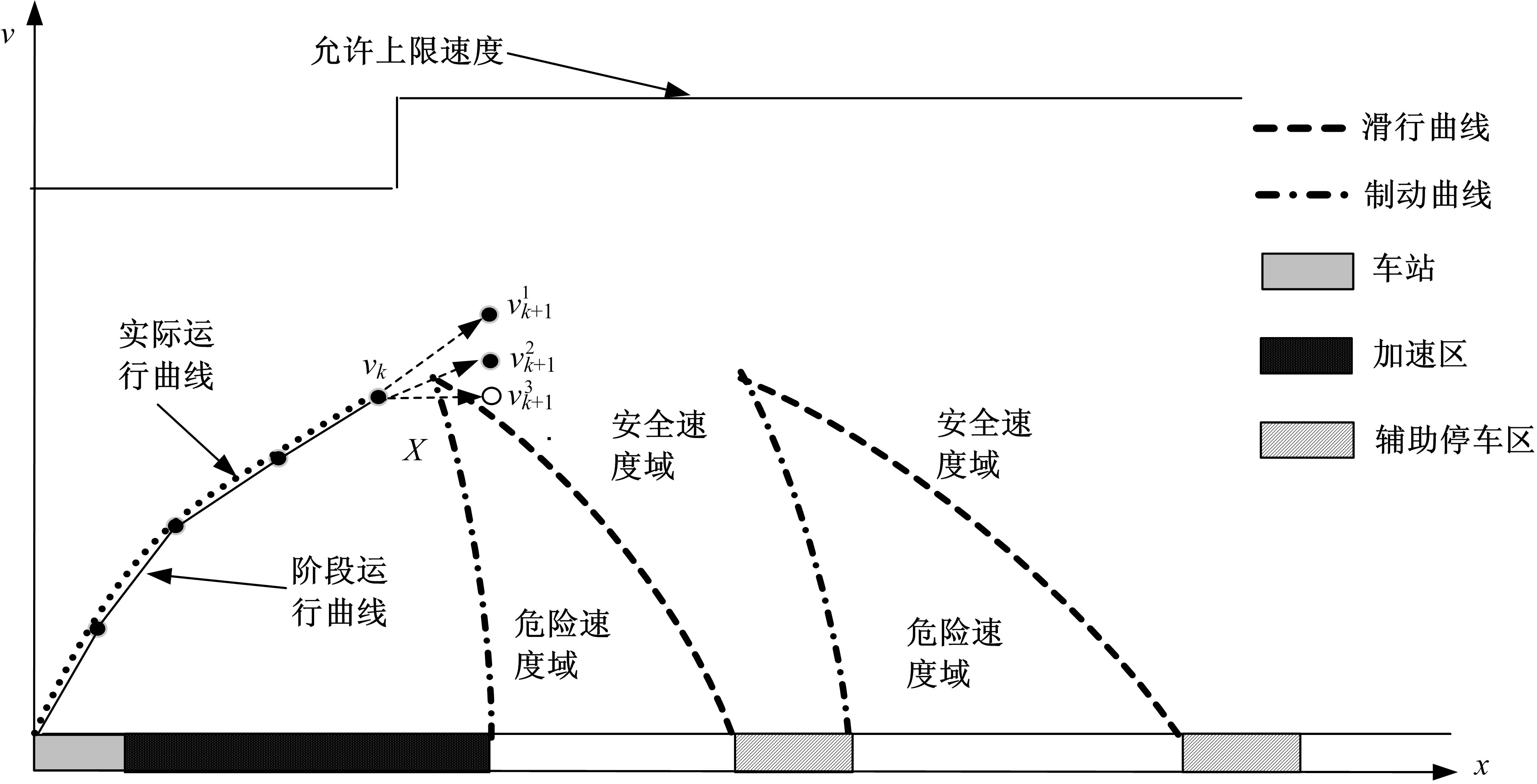
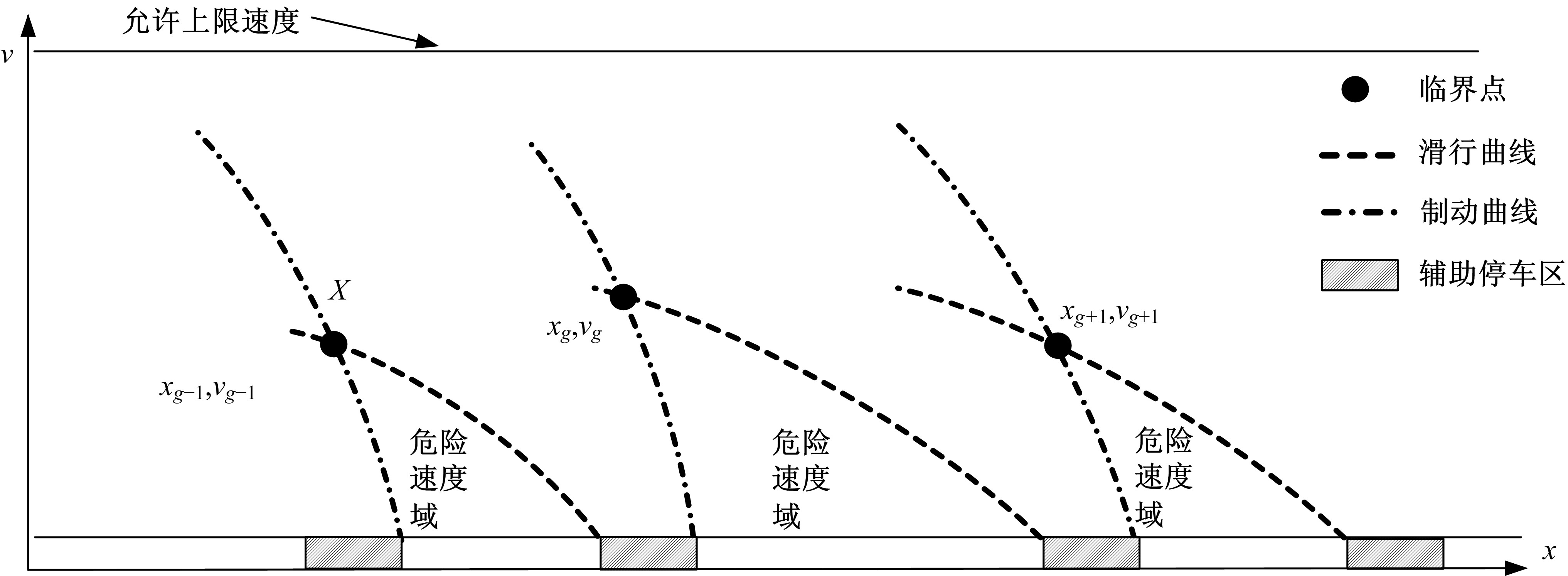
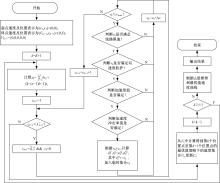
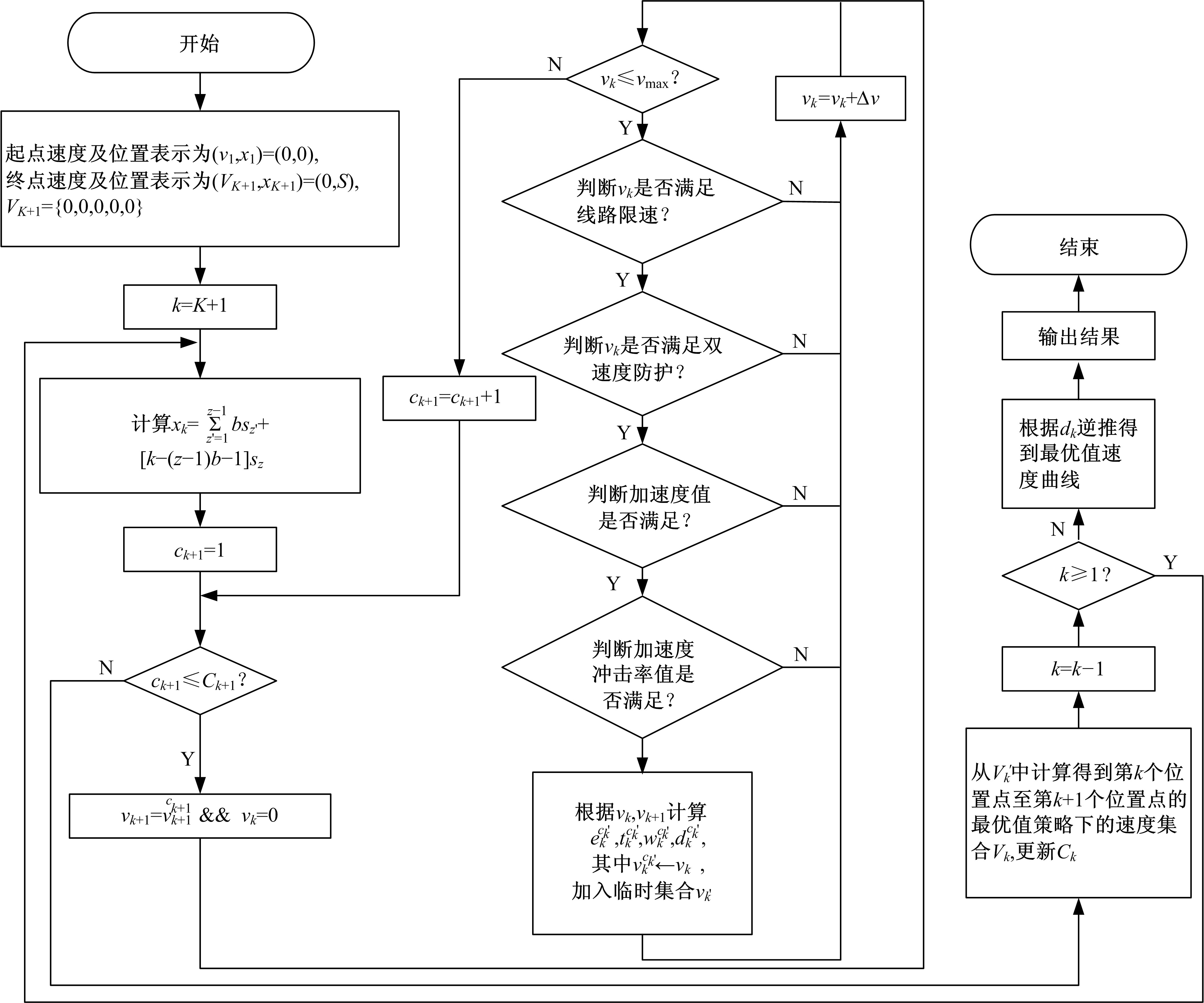
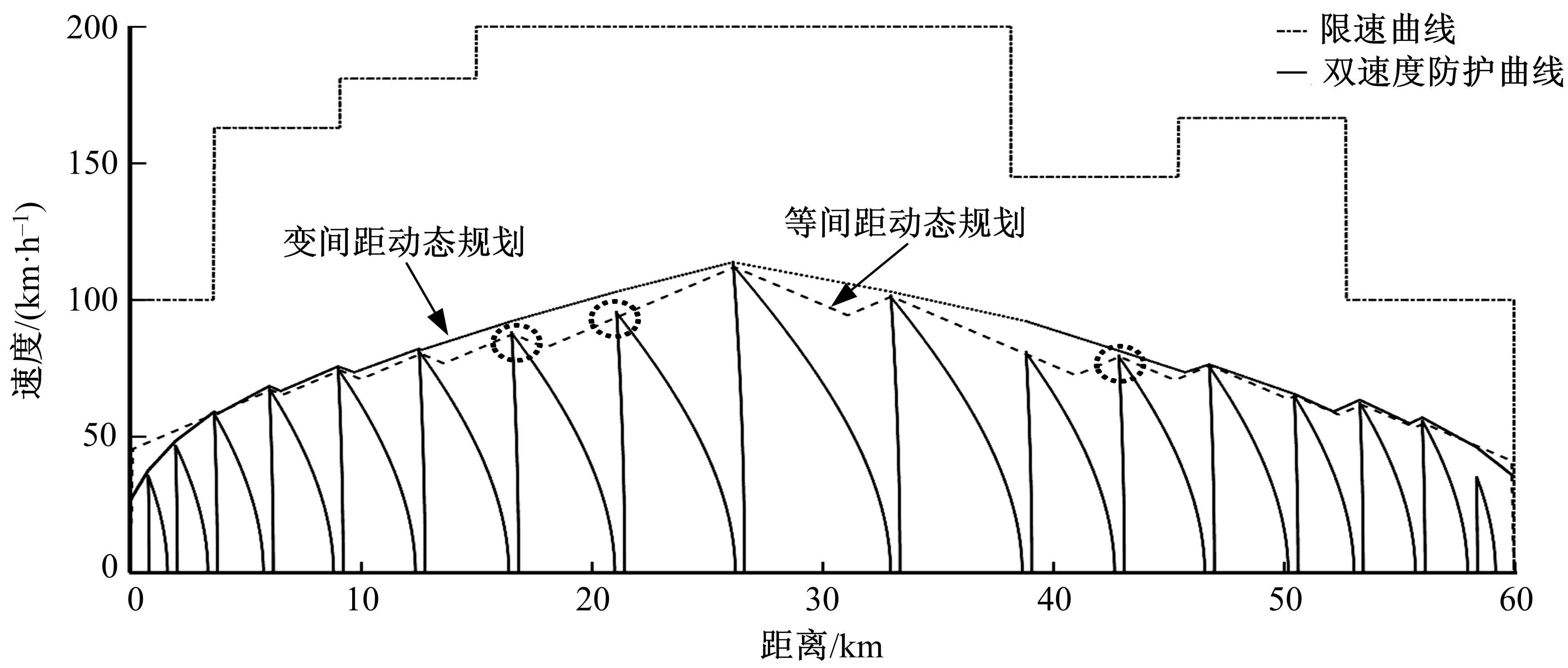
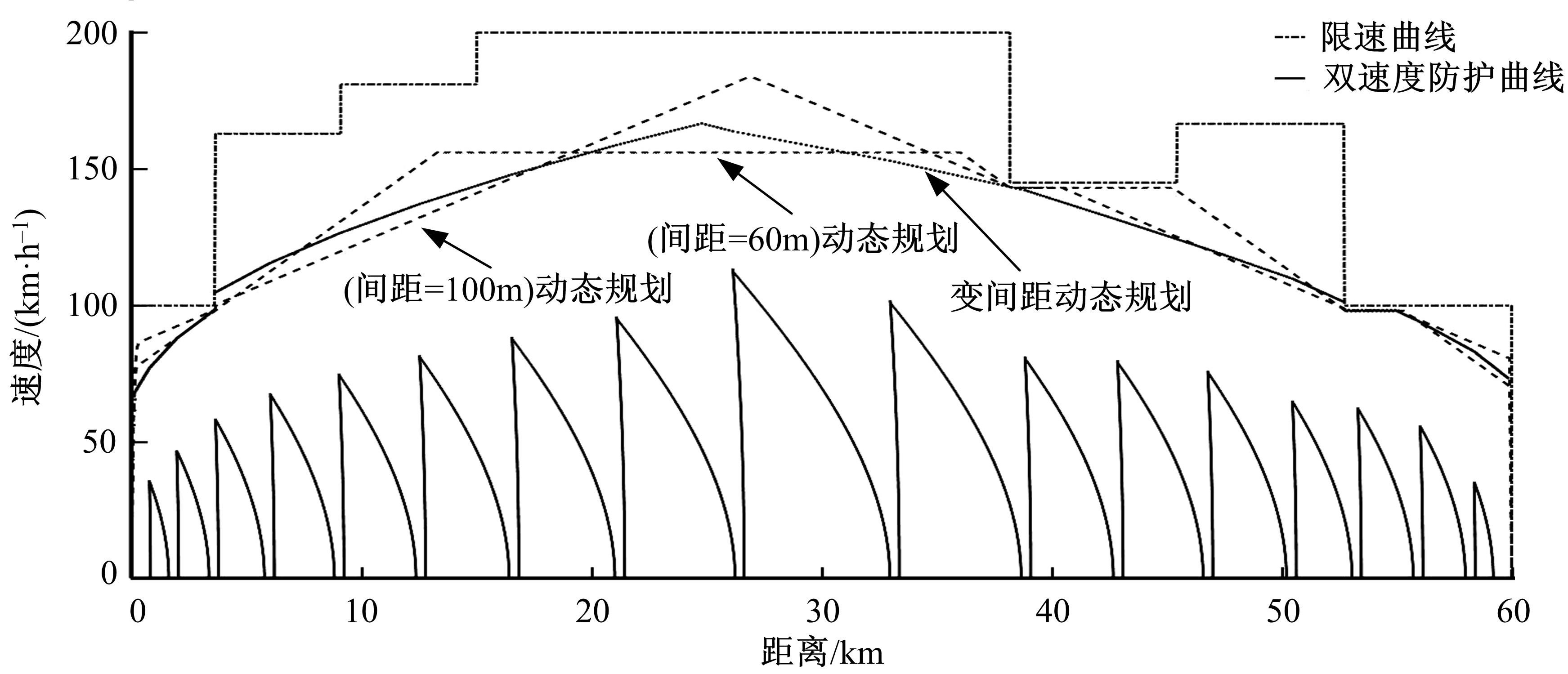
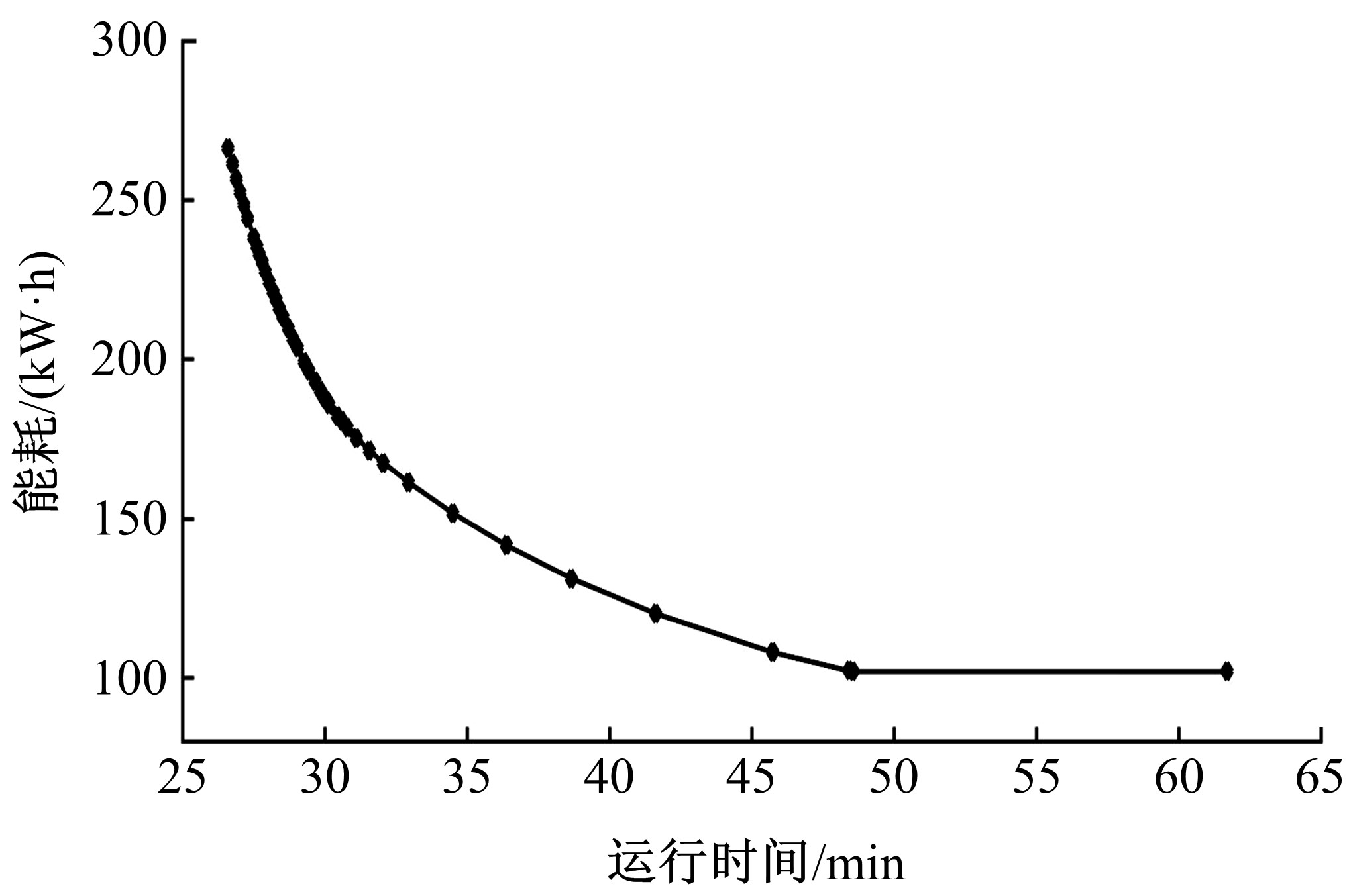
Optimal trajectory planning for middle⁃to⁃high speed maglev based on dynamic programming with mutative spacing

Qing⁃ying LAI1(),Jun LIU1(),Ruo⁃yu ZHAO1,Yong⁃ji LUO2,Ling⁃yun MENG1,Ya⁃zhi XU3   

  1. 1. School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044, China
    2. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 610031, China
    3. CRRC Tangshan Co. , Ltd. , Tangshan 064000, China
  • Received:2018-02-02 Online:2019-05-01 Published:2019-07-12
  • Contact: Jun LIU E-mail:15114243@bjtu.edu.cn;jliu@bjtu.edu.cn

RICH HTML

 3   

PDF (PC)

250

Abstract:

A significant approach to save energy of the middle?to?high speed maglev is to optimize the trajectory planning. This paper establishes a model based on dynamic programming with mutative spacing after analyzing the kinetic equations of the middle?to?high speed maglev and the effect of the assistant?stop area. The model firstly uses the crossover point of double protected curve as the foundation of partition. Then, model further divides the partition into small sub?stages with different spacing and formulates the equation of energy and time respectively. Finally, the model is solved by reversing push method under certain constraints. The established model is compared the conventional dynamic programming method through the numerical examples. The results indicate the advantage of the proposed model in energy saving and computational efficiency.

Key words: railway transportation, middle?to?high speed maglev, optimal trajectory planning, dynamic programming with mutative spacing, assistant?stop area

CLC Number: 

  • U293.1

Fig.1

Sketch map of longitudinal force to Maglev train"

Fig.2

Transfer situation of speed"

Fig.3

Crossover point of double protected curve"

Fig.4

Flow chart of dynamic programming with mutative spacing"

Table 1

Position coordinates of assistant?stop area"

编号起始点/km终止点/km编号起始点/km终止点/km
10.000.821032.9733.38
21.612.041138.6839.10
33.373.771242.6843.11
45.776.201346.5947.01
58.819.231450.2150.63
612.3712.781553.0653.46
716.4116.841655.7256.14
821.0121.441757.9958.41
926.2326.631859.2060.43

Table 2

Limit speed of different sections"

区段/km限速/（km?h–1）
0.0~3.6100
3.6~9.1163
9.1~15.0181
15.0~38.2200
38.2~45.5145
45.5~52.7167
52.7~60.0100

Fig.5

Comparison of optimal trajectory planning in different models (travel time = 50 min)"

Fig.6

Comparison of optimal trajectory planning in different models (travel time = 30 min)"

Table 3

Comparison of parameters in different models (expected travel time = 30 min)"

情况方法间距/m阶段数能耗/(kW·h)时间误差/%计算时长/s
一变间距动态规划-551196.40.67101.3
二等间距动态规划601000186.70.42565.6
三等间距动态规划100600245.20.33125.6

Fig.7

Relationship between energy consumed and"

1 荀径, 杨欣, 宁滨,等. 列车节能操纵优化求解方法综述[J]. 铁道学报, 2014, 36(4): 14⁃20.
XunJing, YangXin, NingBin, et al. Survey on trajectory optimization for train operation[J]. Journal of the China Railway Society, 2014, 36(4): 14⁃20.
2 杨光. 高速磁悬浮列车最优速度曲线及其跟踪控制研究[D]. 北京: 北京交通大学电子信息工程学院, 2007.
YangGuang. Study on high speed maglev train optimum speed curve and its tracking control[D]. Beijing: College of Electronic Information Engineering, Beijing Jiaotong University, 2007.
3 杨轲. 磁悬浮列车仿真平台设计及运控算法研究[D]. 杭州:浙江大学电气工程学院, 2008.
YangKe. Research on maglev train simulation platform design and operation and control algorithm[D]. Hanzhou: College of Electrical Engineering，Zhejiang University, 2008.
4 IchikawaK. Application of optimization theory for bounded state variable problems to the operation of a train[J]. Bulletin of Japanese Society of Mechanical Engineering，1968, 11(47): 857⁃865.
5 MilroyI P. Aspects of automatic train control[D]. Loughborough：Loughborough University, 1980.
6 AsnisI A, DmitrukA V, OsmolovskiiN P. Solution of the problem of the energetically optimal control of the motion of a train by the maximum principle[J]. USSR Computational Mathematics and Mathematical Physics, 1985, 25(6): 37⁃44.
7 KhmelnitskyE. On an optimal control problem of train operation[J]. IEEE Transactions on Automatic Control, 2000, 45(7):1257⁃1266.
8 HowlettP. The optimal control of a train[J]. Annals of Operations Research, 2000, 98(1⁃4):65⁃87.
9 DongH, ZhangL, ChenY, et al. Multi⁃objective train trajectory design based on dynamic programming[C]∥The 33rd Chinese Control Conference (CCC), Nanjing, China, 2014: 9060⁃9065.
10 XuY, ZhaoX, WangL, et al. Optimal control of automatic train operation based on multi⁃scale dynamic programming[C]∥The 33rd Chinese Control Conference (CCC), Nanjing, China, 2014: 3429⁃3433.
11 LuS, HillmansenS, HoT K, et al. Single⁃train trajectory optimization[J]. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(2): 743⁃750.
12 刘进, 吴汶麒. 高速磁悬浮交通二维速度防护曲线及其算法研究[J]. 中国铁道科学, 2002, 23(4):106⁃110.
LiuJin, WuWen⁃lin. Research on 2⁃D speed protection curve and its algorithm of high⁃speed maglev transportation[J]. China Railway Science, 2002, 23(4):106⁃110.
13 江亚, 吴汶麒, 刘进. 磁悬浮列车运行控制系统二维速度防护曲线仿真[J]. 同济大学学报：自然科学版, 2004, 32(3):397⁃400.
JiangYa, WuWen⁃lin, LiuJin, et al. Simulation of high⁃speed maglev train 2⁃D speed protection curve[J]. Journal of Tongji University(Natural Science), 2004, 32(3):397⁃400.
14 杨光, 唐祯敏. 高速磁悬浮列车的安全速度防护问题研究[J]. 北京交通大学学报, 2007, 31(2):38⁃42.
YangGuang, TangZhen⁃min. Study on safety speed protection of the high maglev train[J]. Journal of Beijing Jiaotong University, 2007, 31(2):38⁃42.
15 HowardR A. Dynamic programming[J]. Management Science, 1966, 12(5):317⁃348.
[1] YIN Zi-hong, ZHU Bo, SHAO Guo-xia, KONG De-hui, JIANG Liang-wei. Response of railway track and subgrade under the effect overweight goods [J]. 吉林大学学报(工学版), 2017, 47(5): 1446-1452.
[2] ZUO Jing, SHUAI Bin, HUANG Wen-cheng. Railway emergency rescue program searching based on improved distance entropy MULTIMOORA [J]. 吉林大学学报(工学版), 2017, 47(4): 1068-1074.
[3] NIU Zhi-hui, SU Jian, ZHANG Yi-rui, XU Guan, TAN Fu-xing. Track irregularity simulation based on bogie test rig [J]. 吉林大学学报(工学版), 2017, 47(2): 400-407.
[4] WANG Qi-ming, SU Jian, ZHANG Lan, CHEN Qiu-yu, XU Guan. Forward kinematics of orthogonal Stewart platform based on L-M algorithm [J]. 吉林大学学报(工学版), 2017, 47(1): 97-104.
[5] LIU Yu-mei, ZHAO Cong-cong, XIONG Ming-ye, GUO Wen-cui, ZHANG Zhi-yuan. Reliability assessment of high-speed railway drivetrain based on matter-element model [J]. 吉林大学学报(工学版), 2015, 45(4): 1063-1068.
[6] SHI Huai-long, SONG Ye, WU Ping-bo, ZENG Jing, ZHU Hai-yan. Calculation and testing of suspension stiffness of a bogie of high speed EMU [J]. 吉林大学学报(工学版), 2015, 45(3): 776-782.
[7] WANG Xiu-gang, SU Jian, CAO Xiao-ning, XU Zhen, LU Hai-ge, TIAN Zong-ju. Forward kinematics solution of bogie 6-DOF platform based on the orthogonality of rotation matrix [J]. 吉林大学学报(工学版), 2013, 43(05): 1241-1246.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
Copyright © Journal of Jilin University(Engineering and Technology Edition), All Rights Reserved.
Tel: +86-431-85095297　Fax: +86-431-85094074　E-mail: xbgxb@jlu.edu.cn
Powered by Beijing Magtech Co. Ltd