Journal of Jilin University(Engineering and Technology Edition) ›› 2019, Vol. 49 ›› Issue (3): 865-871.doi: 10.13229/j.cnki.jdxbgxb20180309

Previous Articles     Next Articles

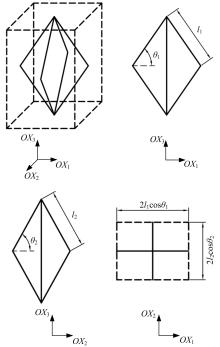
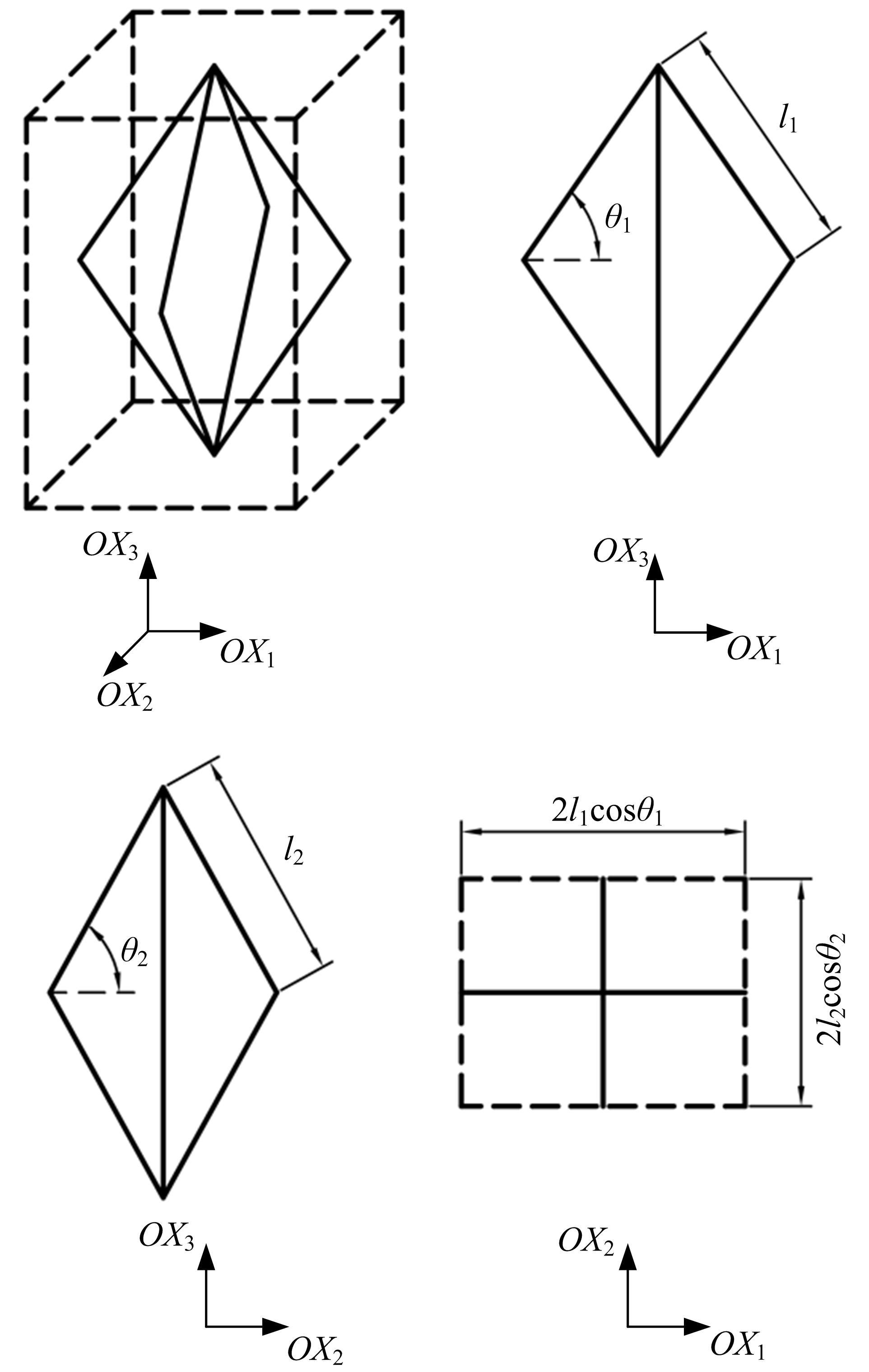
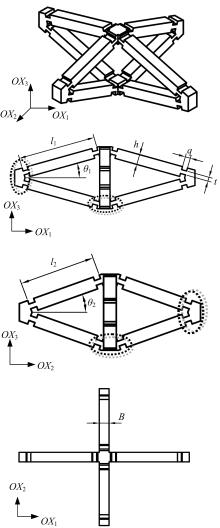
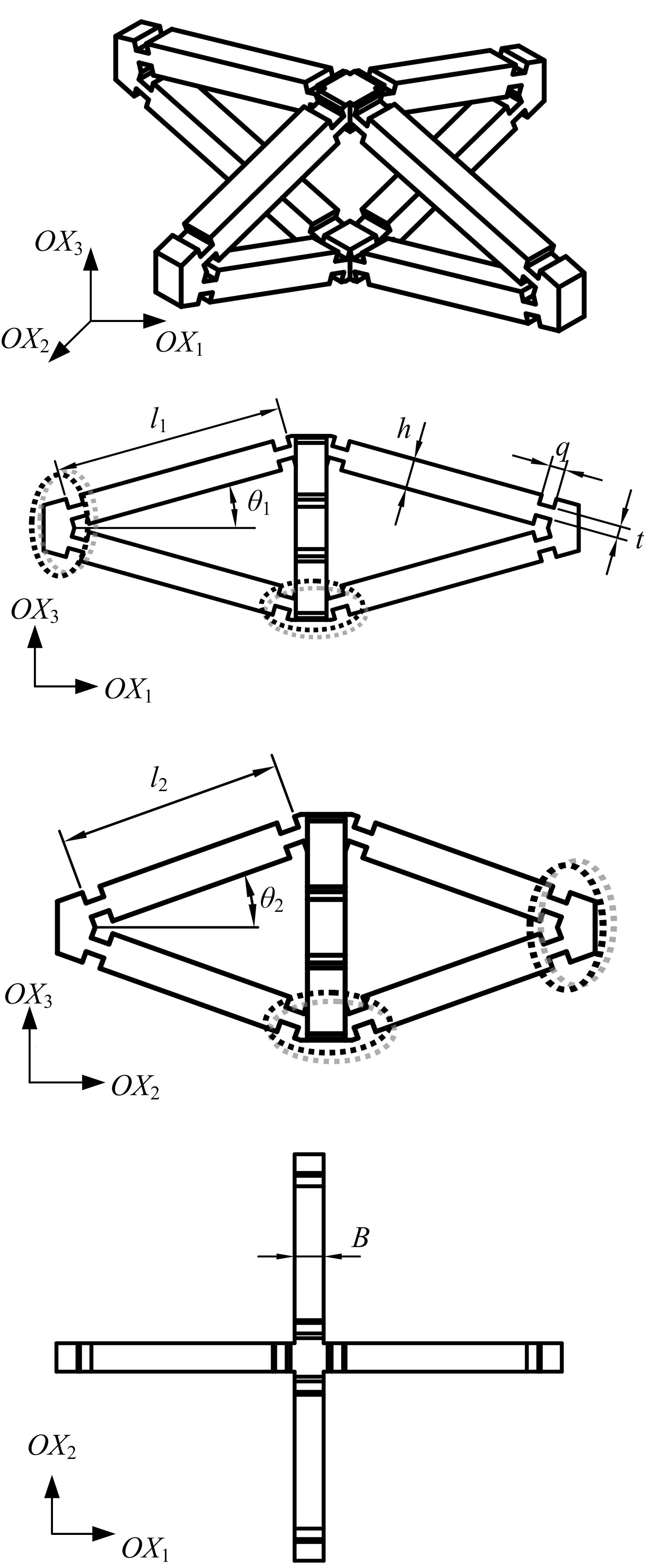
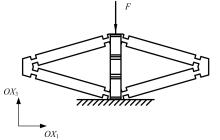
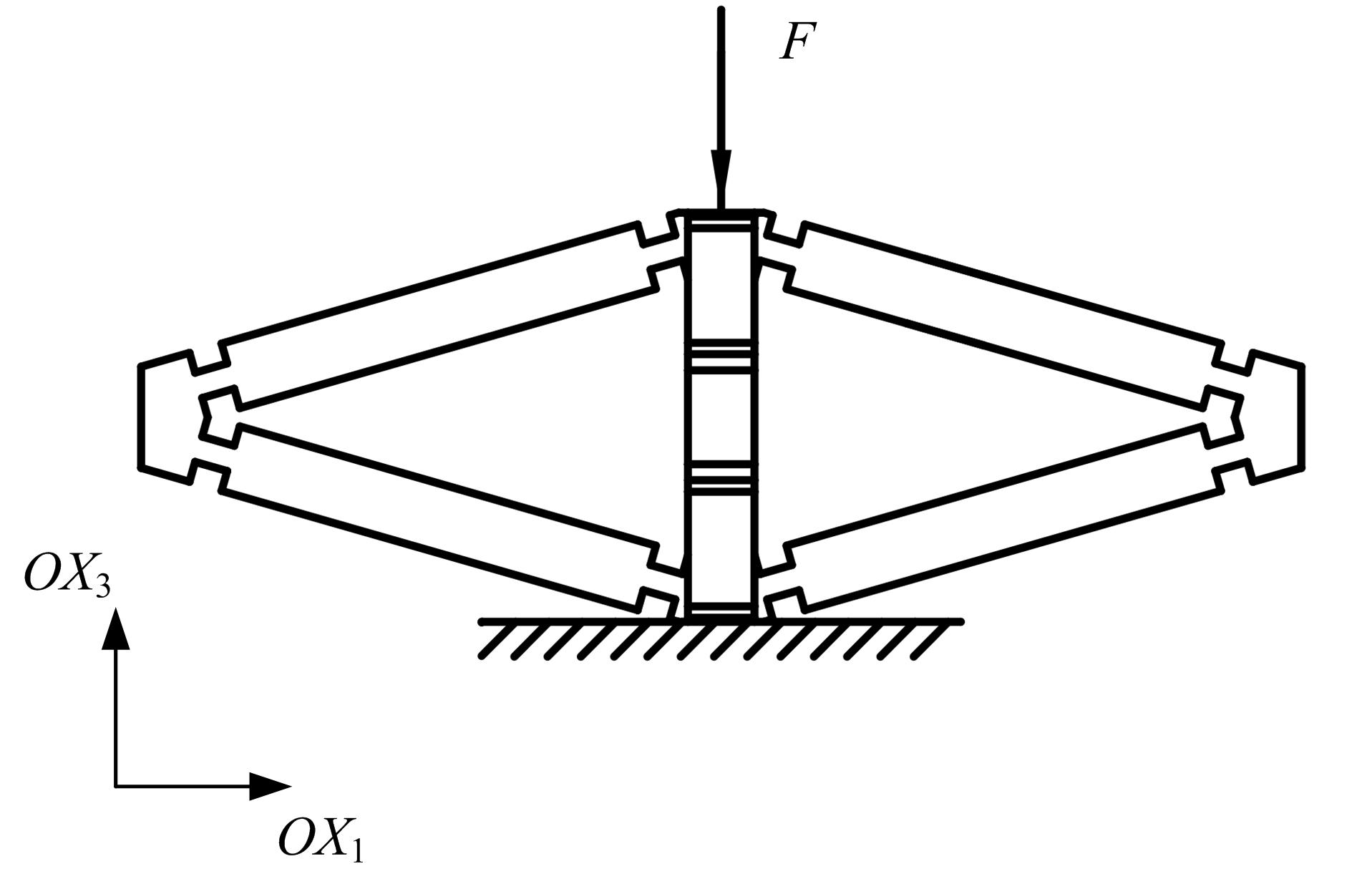
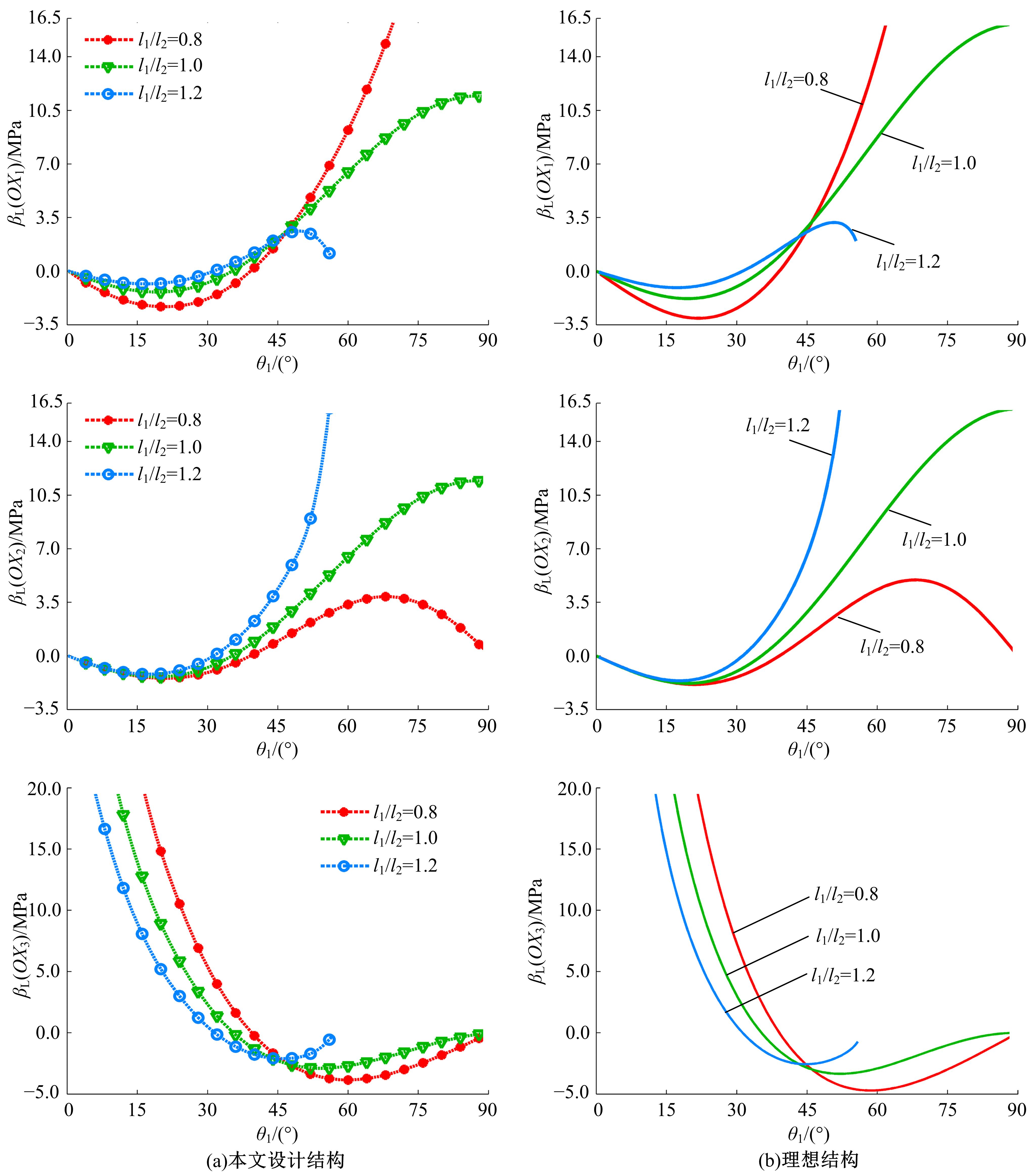
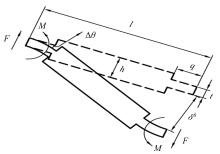
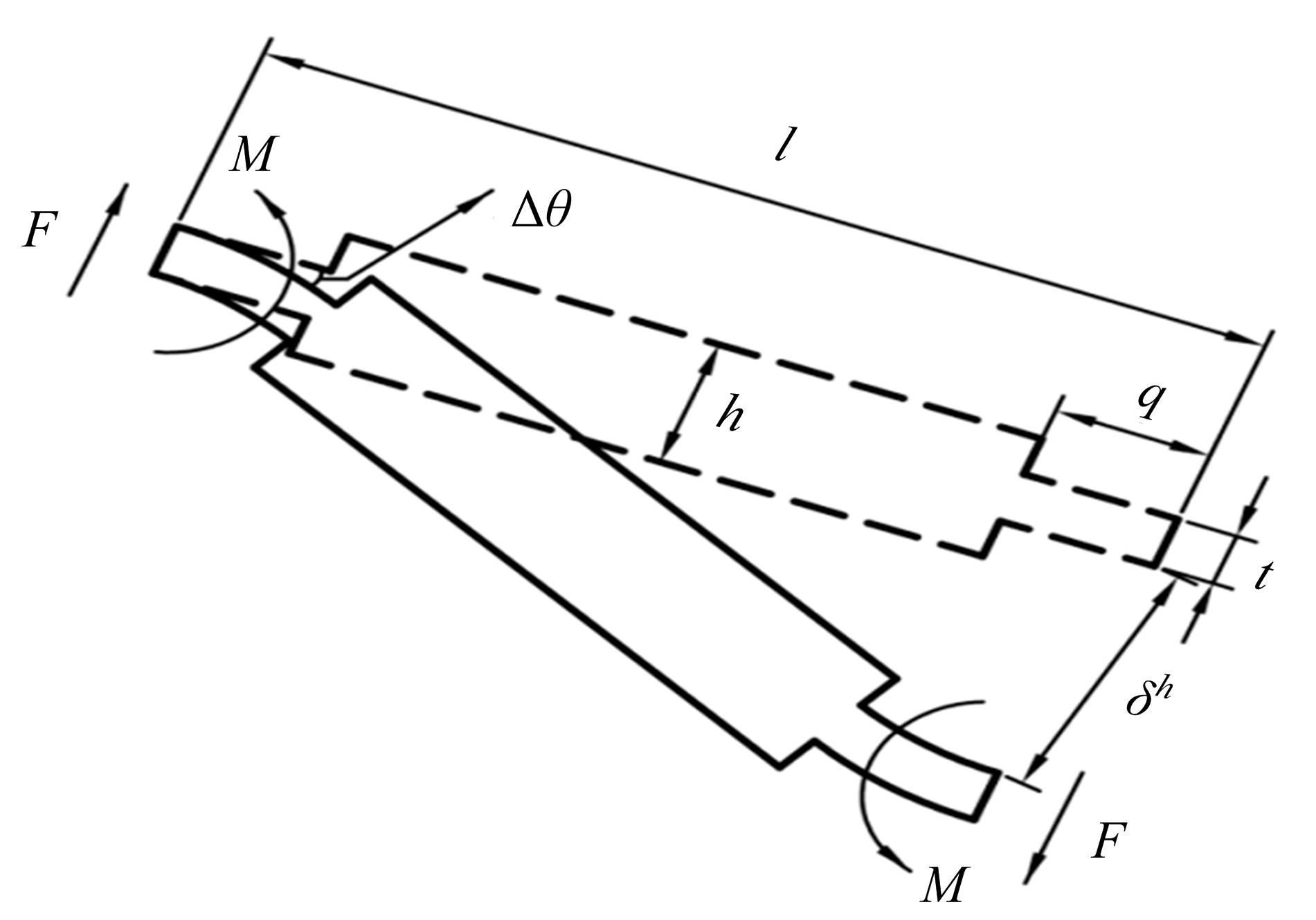
Finite element analysis of hinging octahedron structure withnegative compressibility

Xiao⁃qin ZHOU1(),Lu YANG1,Lei ZHANG1,Li⁃jun CHEN2()   

  1. 1. College of Mechanical Science and Aerospace Engineering, Jinlin University, Changchun 130022, China
    2. Big Data and Network Management Center, Jilin University, Changchun 130022, China
  • Received:2018-04-09 Online:2019-05-01 Published:2019-07-12
  • Contact: Li?jun CHEN E-mail:xqzhou@jlu.edu.cn;clj@jlu.edu.cn

RICH HTML

 5   

PDF (PC)

393

Abstract:

In order to investigate the inherent link between the linear compressibility properties and the geometrical parameters, the 3D hinging octahedron structure was analyzed by a finite element method. With constant geometry size, different finite element models were established by changing the rod length ratio of l1/l2 and angle θ1 between the two rods. The effects of these two structure parameters on the magnitude as well as the range of negative linear compressibility (i.e. NLC) of this structure were analyzed and discussed. It is shown that through carefully choosing the geometry parameters, NLC can be exhibited in this model along the three?axis directions. More specifically, the sign of the linear compressibility is determined by the angle θ1 while the magnitude and range of NLC are determined by the l1/l2 ratio.

Key words: solid mechanics, negative compressibility, finite element method, hinging octahedron structure

CLC Number: 

  • O342

Fig.1

Idealised hinging octahedron model and its two?dimensional projections in three axes"

Fig.2

Dimensions of finite element model of octahedron model"

Fig.3

Schematic diagram of hinging octahedronmodel when subjected to force along oneon?axis direction"

Fig.4

Simulated linear compressibilities of hinging octahedron model compared with theoretical results predicated by idealised hinging model"

Fig.5

Deformation analysis of the flexure hinge"

1 MorosinB, SchirberJ E. Linear compressibilities and the pressure dependence of the atomic positional parameter of As[J]. Solid State Communications, 1972, 10(3): 249⁃251.
2 SkeltonE F, FeldmanJ L, LiuC Y, et al. Study of the pressure⁃induced phase transition in paratellurite (TeO2)[J]. Physical Review B, 1976, 13(6): 2605⁃2613.
3 MariathasanJ W E, FingerL W, HazenR M. High⁃pressure behavior of LaNbO4[J]. Acta Crystallographica Section B: Structural Science, 1985, 41(3): 179⁃184.
4 FortesA D, SuardE, KnightK S. Negative linear compressibility and massive anisotropic thermal expansion in methanol monohydrate[J]. Science, 2011, 331(6018): 742⁃746.
5 BaughmanR H, StafstromS, CuiC, et al. Materials with negative compressibility in one or more dimensions[J]. Science, 1998, 279(5356): 1522⁃1524.
6 GrimaJ N, AttardD, Caruana⁃GauciR, et al. Negative linear compressibility of hexagonal honeycombs and related systems[J]. Scripta Materialia, 2011, 65(7): 565⁃568.
7 BarnesD L, MillerW, EvansK E, et al. Modelling negative linear compressibility in tetragonal beam structures[J]. Mechanics of Materialia, 2012, 46: 123⁃128.
8 GrimaJ N, Caruana⁃GauciR, WojciechowskiK W, et al. Smart hexagonal truss systems exhibiting negative compressibility through constrained angle stretching[J]. Smart Materials and Structures, 2013, 22(8): 84015.
9 GrimaJ N, AttardD, GattR. Truss⁃type systems exhibiting negative compressibility[J]. Physical Status Solidi, 2008, 245(11): 2405⁃2414.
10 ChoiJ B, LakesR S. Analysis of elastic modulus of conventional foams and of re⁃entrant foam materials with a negative Poisson's ratio[J]. International Journal of Mechanical Science, 1995, 37(1): 51⁃59.
11 ChoiJ B, LakesR S. Nonlinear analysis of the Poisson's ratio of negative Poisson's ratio foams[J]. Journal of Composite Materials, 1995, 29(1): 113⁃128.
12 LuZ X, LiuQ, YangZ Y. Predictions of Young's modulus and negative Poisson's atio of auxetic foams[J]. Physica Status Solidi B, 2011, 248: 167⁃174.
13 LiK, GaoX L, RoyA K. Micromechanics model for three⁃dimensional open⁃cell foams using a tetrakaidecahedral unit cell and Castigliano's second theorem[J]. Composites Science and Technology, 2003, 63(12): 1769⁃1781.
14 GrimaJ N, Caruana⁃GauciR, AttardD,et al. Three⁃dimensional cellular structures with negative Poisson's ratio and negative compressibility properties[J]. Proceedings of the Royal Society A: Mathematical Physical and Engineering Sciences, 2012, 468(2146): 3121⁃3138.
15 XieY M, YangX Y, ShenJ H et. al. Designing orthotropic materials for negative or zero compressibility[J]. International Journal of Solids and Structures, 2014, 51(23/24): 4038⁃4051.
16 ZhouX Q, ZhangL, ZhangH, et al. 3D cellular models with negative compressibility through the wine⁃rack⁃type mechanism: 3D cellular models with negative compressibility[J]. Physica Status Solidi, 2016, 253(10): 1977⁃1993.
17 MastersI G, EvansK E. Models for the elastic deformation of honeycombs[J]. Composite Structures, 1996, 35: 403⁃422.
[1] BI Qiu-shi,WANG Guo-qiang,HUANG Ting-ting,MAO Rui,LU Yan-peng. Tooth strength analysis of mineral sizer by coupling discrete element method and finite element method [J]. Journal of Jilin University(Engineering and Technology Edition), 2018, 48(6): 1770-1776.
[2] WANG Jing-yu, YU Xu-tao, HU Xing-jun, GUO Peng, XIN Li, GUO Feng, ZHANG Yang-hui. Fluid-induced vibration and flow mechanism of automotive external rearview mirror [J]. 吉林大学学报(工学版), 2017, 47(6): 1669-1676.
[3] SUN Rong-jun, GU Shuan-cheng, JU Pei, GAO Ke. Optimal design of new arc angle PDC drill bit for coal mining based on finite element method [J]. 吉林大学学报(工学版), 2017, 47(6): 1991-1998.
[4] ZHANG Yun-long, LIU Zhan-ying, WU Chun-li, WANG Jing. Static and dynamic responses of steel-concrete composite beams [J]. 吉林大学学报(工学版), 2017, 47(3): 789-795.
[5] LIU Yu, LI Peng-fei, ZHANG Yi-min. Analysis and prediction of micro milling deformation of copper thin-wall parts [J]. 吉林大学学报(工学版), 2017, 47(3): 844-849.
[6] LIU Cheng, SHI Wen-ku, CHEN Zhi-yong, HE Wei, RONG Ru-song, SONG Huai-lan. Experiment on tooth root bending stress of driving axle hypoid gear of automobile [J]. 吉林大学学报(工学版), 2017, 47(2): 344-352.
[7] YAN Guang, ZHUANG Wei, LIU Feng, ZHU Lian-qing. Preload package and characteristics of a sensitizing effect sensor based Fiber Bragg Grating (FBG) [J]. 吉林大学学报(工学版), 2016, 46(5): 1739-1745.
[8] ZHUANG Ye, CHEN Yu-hang, YANG Ye-hai, XU Shu-fang. Twin-tube hydraulic shock absorber F-V modeling based on structure parameters [J]. 吉林大学学报(工学版), 2016, 46(3): 732-736.
[9] LIU Han-bing, SHI Cheng-lin, TAN Guo-jin. Finite element solution of composite beam with effect of shear slip [J]. 吉林大学学报(工学版), 2016, 46(3): 792-797.
[10] XIAO Xiang, HUANG En-hou, NI Ying-sheng. Theoretical analysis and experiment of the effect of flange width on beam-plates system of prestressed concrete [J]. 吉林大学学报(工学版), 2015, 45(6): 1784-1790.
[11] MENG Guang-wei,LI Xiao-lin,LI Feng,ZHOU Li-ming,WANG Hui. Smoothed multiscale finite element method for flow in fractured media [J]. 吉林大学学报(工学版), 2015, 45(2): 481-486.
[12] FU Zhi-qiang,AN Zi-jun,DU Feng-shan,DUAN Li-ying,YU Hui,YANG Fan. Elongation of rectangular tube in continuous roll forming [J]. 吉林大学学报(工学版), 2015, 45(2): 487-493.
[13] MA Yao, DONG Xiao-long, LI Ze-jun, SHEN Lin, ZHAO Hong-wei. Finite element simulation of the effect of different initial contact on nano-indentation [J]. 吉林大学学报(工学版), 2014, 44(5): 1366-1370.
[14] MA Biao, ZHAO Jia-xin, LI He-yan, NING Ke-yan, HE Chun-ping. Effect of clutches' structural parameters on thermalelastic instability [J]. 吉林大学学报(工学版), 2014, 44(4): 933-938.
[15] LI Xiao-jun,LIANG Lu-lu,XIE Cheng-wei,YANG Shuo. Auto-generation and application of virtual mechanical simulation model of asphalt concrete [J]. 吉林大学学报(工学版), 2014, 44(3): 655-660.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
Copyright © Journal of Jilin University(Engineering and Technology Edition), All Rights Reserved.
Tel: +86-431-85095297　Fax: +86-431-85094074　E-mail: xbgxb@jlu.edu.cn
Powered by Beijing Magtech Co. Ltd