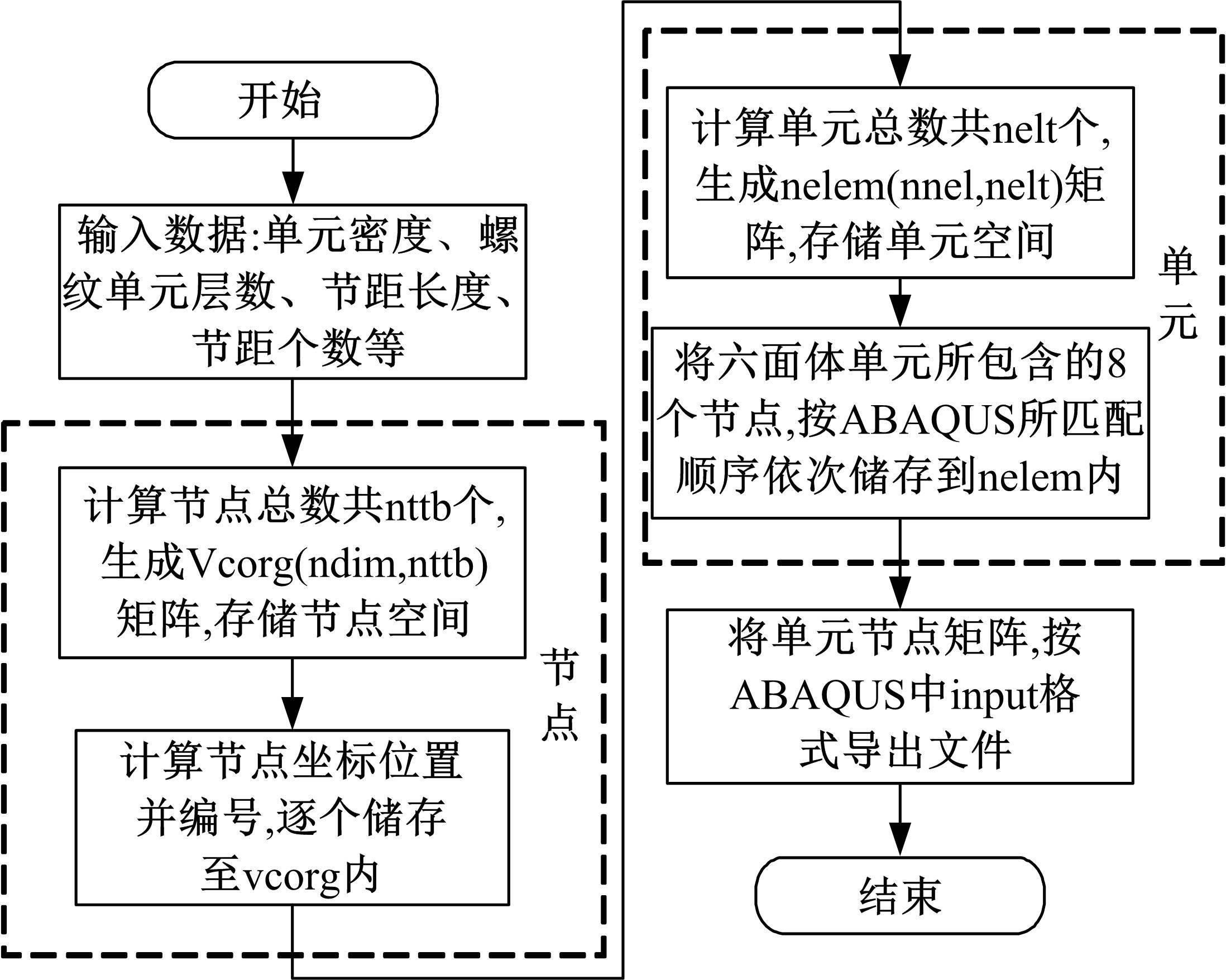
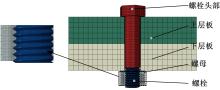
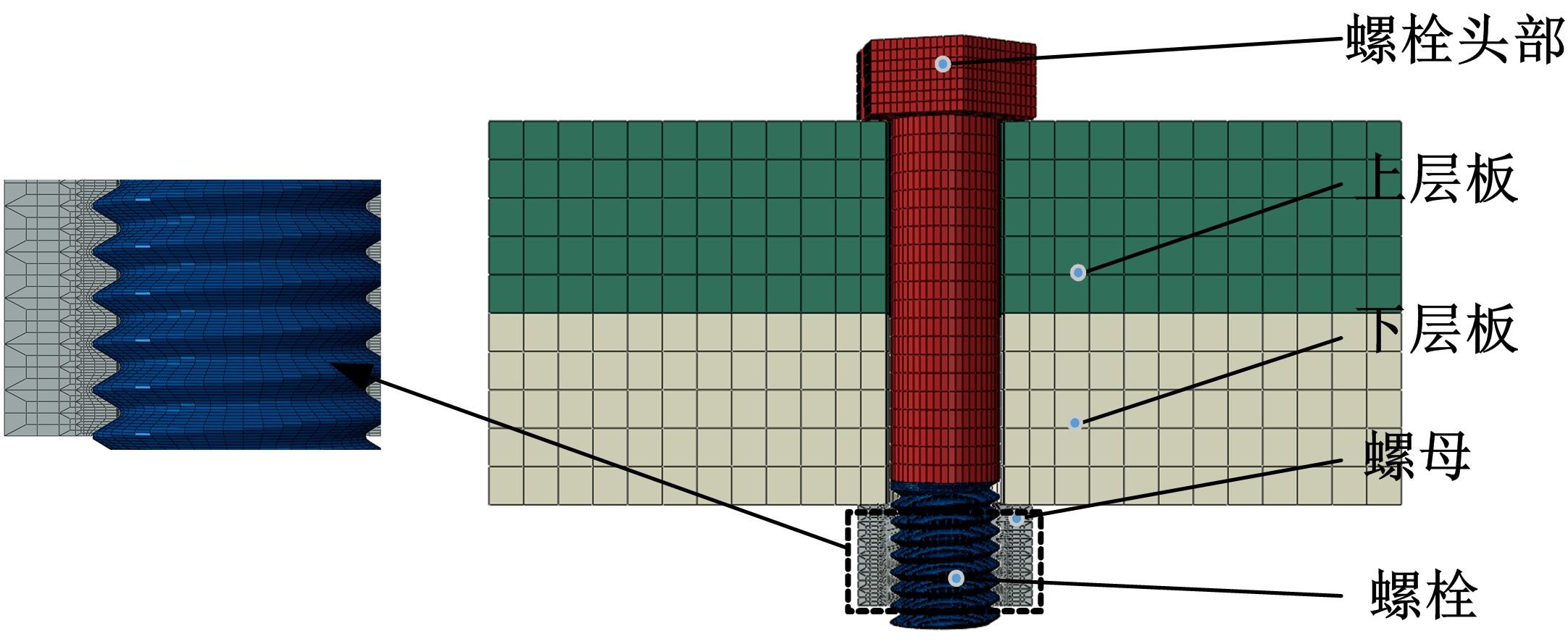
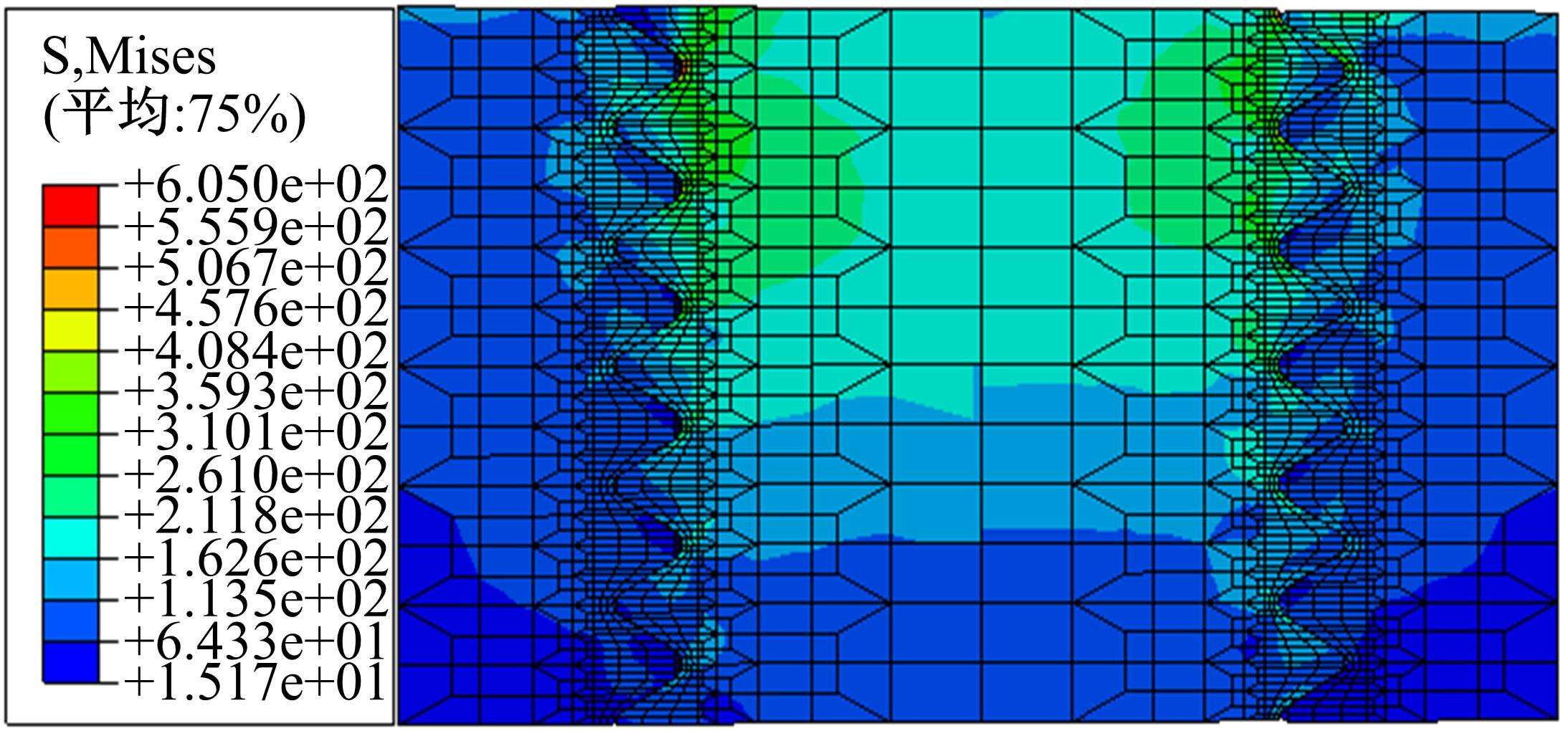
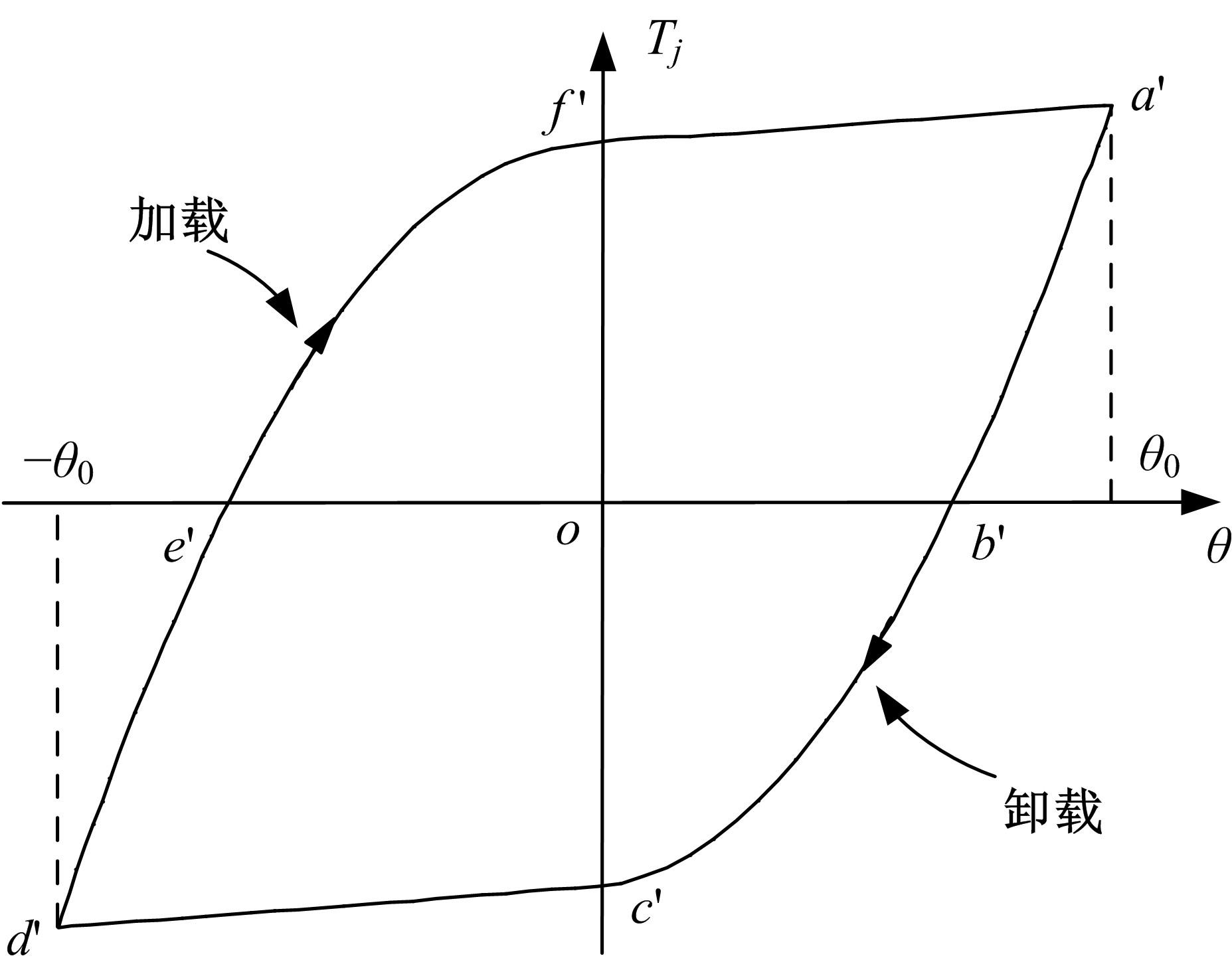
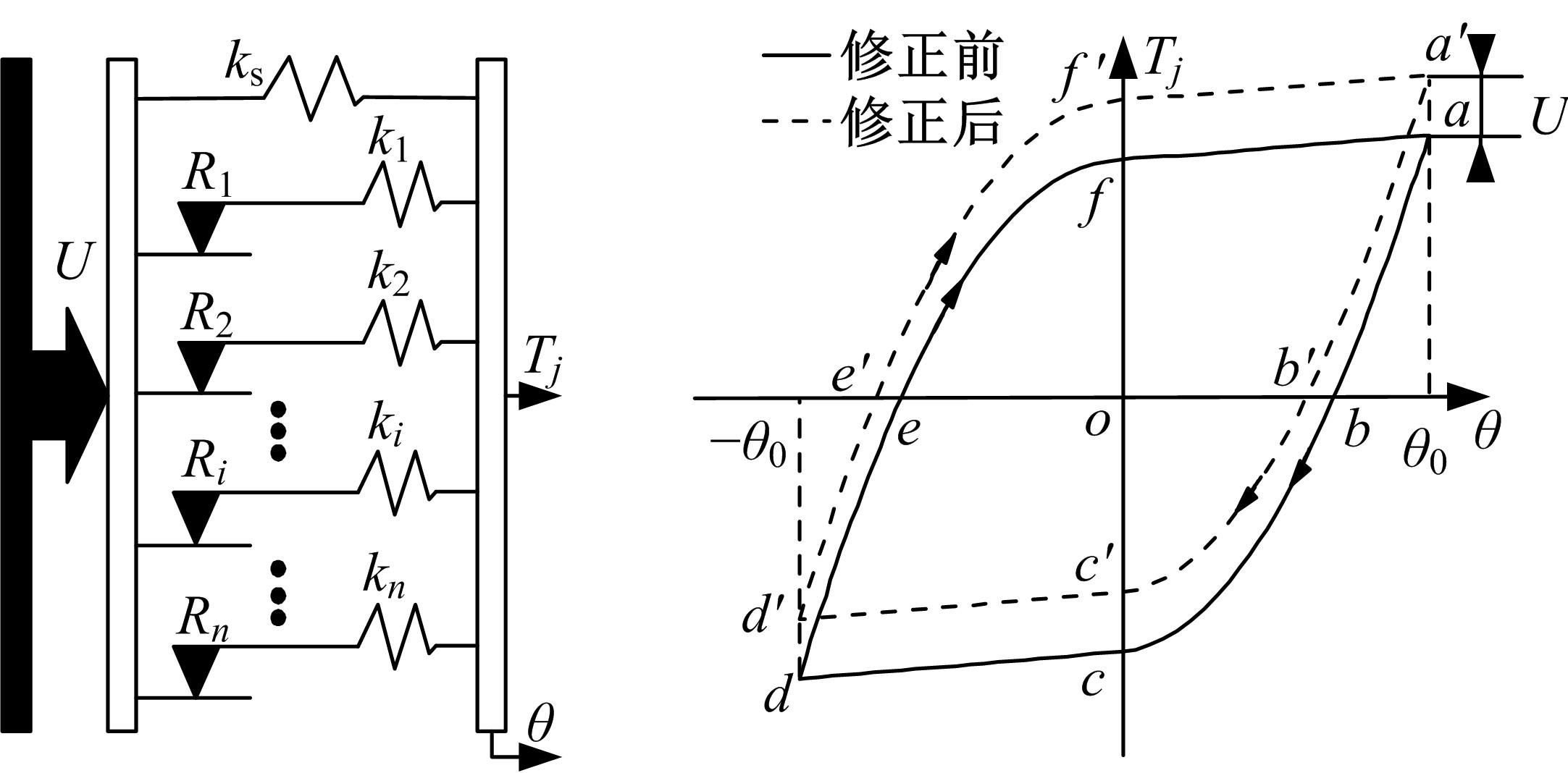
Journal of Jilin University(Engineering and Technology Edition) ›› 2023, Vol. 53 ›› Issue (5): 1305-1314.doi: 10.13229/j.cnki.jdxbgxb.20210914

Previous Articles    

Modified IWAN model of helical threaded connector imposed to torsional load

Jiu-yi LI1(),Feng-jun ZHOU1(),Jian-hua LIU2,Yun-hou SUN1,Jing-zhong ZHU1,Ming-kun QIU3   

  1. 1.National Defense Engineering Research Institute，Academy of Military Science of PLA，Beijing 100850，China
    2.School of Materials Science and Engineering，Southwest Jiao Tong University，Chengdu 610031，China
    3.Internal Control Audit Center of PLA General Hospital，Beijing 100850，China
  • Received:2021-09-13 Online:2023-05-01 Published:2023-05-25
  • Contact: Feng-jun ZHOU E-mail:jylee.swjtu@foxmail.com;zhoufj@cae.cn

RICH HTML

 4   

PDF (PC)

140

Abstract:

A three-dimensional finite element model of spiral thread is established in the paper， and the effectiveness of the model scheme is verified by the numerical calculations of "stress distribution on the surface of thread"， the mechanical properties of threaded structure under torsional load are numerically studied. The results show that： The thread structure experiences three states： adhesion， partial slip and macro slip in the loading and unloading stages； In the macro sliding stage of the tightening process， the torque increases due to the increase of axial force， and decreases due to the decrease of axial force in the loosening process. Based on the finite element calculation results of threaded structure， for the three-dimensional threaded structure with lifting angle under torsional load， the modified IWAN model is established by adding the overall correction of residual stiffness and torque during macro slip. The calculation results show that the modified IWAN model can accurately reproduce the relationship between torque and rotation angle in the finite element simulation results， The modified IWAN model composed of three Jenkins element models can accurately restore the dissipated energy obtained by finite element simulation.

Key words: engineering mechanics, thread structure, finite element modeling, torsional load, IWAN model

CLC Number: 

  • TH112

Fig.1

Thread section along the central axis of the bolt"

Fig.2

Sketch diagram of external thread profile"

Fig.3

Modeling platform main interface"

Fig.4

Model building process"

Fig.5

Integral finite element model of threaded connection components"

Table 1

Material parameters of each component"

部件（材料）密度/ （kg·m-3）弹性模量 /MPa泊松比
螺栓（35CrMn）7.87213 0000.286
螺母（45钢）7.87209 0000.269
板（碳钢）7.87210 0000.280

Table 2

Plastic strain behavior of bolt and nut"

螺栓（35CrMn）螺母（45钢）
应力/MPa塑性应变应力/MPa塑性应变
48004000
5000.002 824200.001 52
5800.0125000.0295
6800.0456300.056
8500.117000.095
10000.37600.25

Fig.6

Equivalent stress contour"

Fig.7

Plastic strain contour"

Table 3

Summary of finite element calculation conditions"

工况序号Cont2Cont3扭转角度/rad预紧力/kN
10.10.10.0055
20.10.10.00510
30.10.10.00520
40.10.10.00220
50.10.10.003520
60.050.10.00520
70.150.10.00520
80.10.050.00520
90.10.150.00520

Fig.8

Influence of Fp， A，μh and μb on the dynamic response of threaded connection structures"

Fig.9

Hysteresis curve of classical IWAN model"

Fig.10

Hysteresis curve incorporated ks"

Fig.11

Modified IWAN model with integral torque correction and its hysteretic curve"

Fig.12

Modified IWAN model with modified residual stiffness and its hysteretic curve"

Table 4

Parameter extraction results of Jenkins unit model with different number"

滞回曲线类型kiRi单周期耗散能/J
有限元模拟//451.34
经典IWAN//453.26
1阶修正k1=15.70R1=68.50367.04
2阶修正k1=23.09R1=52.06438.58
k2=6.90R2=16.43
3阶修正k1=26.81R1=42.03440.10
k2=13.65R2=21.60
k3=4.01R3=4.87
公共修正项ks=0.64；U=12.179 15 N?m；kp=0.55

Fig.13

Modified IWAN model hysteresis curve"

1 侯世远, 廖日东. 螺纹联接松动过程的研究现状与发展趋势[J]. 强度与环境, 2014(2): 39-52.
Hou Shi-yuan, Liao Ri-dong. Research progress on self-loosening of threaded fasteners[J]. Structure and Environment Engineering, 2014(2): 39-52.
2 Fukuoka T, Nomura M. Proposition of helical thread modeling with accurate geometry and finite element analysis[J]. ASME Journal of Pressure Vessels and Piping Technology, 2008, 130(1): 011204.
3 Hess D P, Basava S, Rasquinha I A. Variation of clamping force in a single-bolt assembly subjected to axial vibration[J]. Journal of Mechanical Design, 1996, 90(1): 97-102.
4 施刚, 石永久, 王元清. 钢结构梁柱连接节点域剪切变形计算方法[J]. 吉林大学学报: 工学版, 2006,36(4): 462-466.
Shi Gang, Shi Yong-jiu, Wang Yuan-qing. Calculational method of shear deform action for beam-to-column connection panel zone in steel frames[J]. Journal of Jilin University(Engineering and Technology Edition), 2006, 36(4): 462-466.
5 庄蔚敏, 赵文增, 解东旋, 等. 超高强钢/铝合金热铆连接接头性能[J]. 吉林大学学报: 工学版, 2018, 48(4): 1016-1022.
Zhuang Wei-min, Zhao Wen-zeng, Xie Dong-xuan, et al. Joint performance analysis on connection of ultrahigh-strength steel and aluminum alloy with hot riveting[J]. Journal of Jilin University(Engineering and Technology Edition), 2018, 48(4): 1016-1022.
6 Junker H G. Criteria for self loosening of fasteners under vibration[J]. Aircraft Engineering and Aerospace Technology, 1972, 44(10): 14-16.
7 Jiang Y, Chang J, Lee C H. An experimental study of the torque-tension relationship for bolted joints[J]. International Journal of Materials and Product Technology, 2001, 16(4/5): 417-429.
8 Liu J H, Ouyang H J, Feng Z Q. Study on self-loosening of bolted joints excited by dynamic axial load[J]. Tribology International, 2017, 115: 432-451.
9 Liu J H, Ouyang H J, Ma L J. Numerical and theoretical studies of bolted joints under harmonic shear displacement[J]. Latin American Journal of Solids and Structures, 2015, 12(1): 115-132.
10 Wriggers P. Computational Contact Mechanics[M]. Berlin: Wiley, 2002.
11 van Basshuysen R, Schäfer F. Internal Combustion Engine Handbook: Basics, Components, Systems, and Perspectives[M]. Warrendale: SAE International, 2004.
12 Gaul L, Nitsche R. The role of friction in mechanical joints[J]. Applied Mechanics Reviews, 2001, 54: 93-106.
13 Gaul L, Lenz J. Nonlinear dynamics of structures assembled by bolted joints[J]. Acta Mechanica, 1997, 125(1): 169-181.
14 Liu J H, Ouyang H J. Dynamic behaviour of a bolted joint subjected to torsional excitation[J]. Tribology International, 2019, 140: 105877.
15 Valanis K C. Fundamental consequences of a new intrinsic time measure: plasticity as a limit of the endochronic theory[J]. Archiwum Mechaniki Stossowanej, 1980, 32(2): 171-191.
16 Ikhouane F, Hurtado J E, Rodellar J. Variation of the hysteresis loop with the Bouc-Wen model parameters[J]. Nonlinear Dynamics, 2007, 48(4): 361-380.
17 Wen Y K. Methods of random vibration for inelastic structures[J]. Applied Mechanics Reviews, 1989, 42(2): 39-52.
18 Iwan W D, A distributed-element model for hysteresis and its steady-state dynamic response[J]. Journal of Applied Mechanics, 1966, 33(4): 893-900.
19 张相盟, 王本利, 卫洪涛. Iwan模型非线性恢复力及能量耗散计算研究[J]. 工程力学, 2012, 29(11): 33-39.
Zhang Xiang-meng, Wang Ben-li, Wei Hong-tao. Calculation of nonlinear restoring forces and energy dissipation of Iwan model[J]. Engineering Mechanics, 2012, 29(11): 33-39.
20 Iwan W D. On a class of models for the yielding behavior of continuous and composite systems[J]. Journal of Applied Mechanics, 1967, 34(3): 612-617.
21 全国螺纹标准化技术委员会. 公制、美制和英制螺纹标准手册[M]. 3版. 北京: 中国标准出版社, 2009.
22 Eramo M D, Cappa P. An experimental validation of load distribution in screw threads[J]. Experimental Mechanics, 1991, 31(1): 70-75.
23 濮良贵, 陈国定, 吴立言. 机械设计[M]. 9版. 北京: 高等教育出版社, 2013.
24 Segalman D J, Starr M J. Inversion of masing models via continuous Iwan systems[J]. International Journal of Non-linear Mechanics, 2008, 43(1): 74-80.
[1] Guang-wei MENG,Chuan-xin REN,Feng LI,Tong-hui WEI. Interval analysis of structural fatigue life under random load [J]. Journal of Jilin University(Engineering and Technology Edition), 2022, 52(1): 46-52.
[2] Bi⁃xiong LI,Qiao LIAO,Yi⁃ping ZHANG,Lian ZHOU,Ping WEI,Kan LIU. Theoretical on flexural behavior of ultra high strength rebar reinforced engineered cementitious composites beam [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(4): 1153-1161.
[3] NI Ying-sheng,SUN Qi-xin,MA Ye,XU Dong,LIU Chao. Shear distribution of multi-cell corrugated steel web composite beams based on space grid analysis [J]. Journal of Jilin University(Engineering and Technology Edition), 2018, 48(6): 1735-1746.
[4] YAN Ya-bin, WANG Xiao-yuan, WAN Qiang. Low-cycle fatigue fracture behavior of nanoscale interface [J]. 吉林大学学报(工学版), 2017, 47(4): 1201-1206.
[5] CHEN Jiang-yi, LIU Bao-yuan. Influence of fiber fracture damage on dispersion characteristic of guided wave in composite plate [J]. 吉林大学学报(工学版), 2017, 47(1): 180-184.
[6] MENG Guang-wei, FENG Xin-yu, ZHOU Li-ming, Li Feng. Structural reliability analysis based on dimension reduction algorithm [J]. 吉林大学学报(工学版), 2017, 47(1): 174-179.
[7] LI Chun-liang, WANG Fang-yan, ZHANG Li-hui, WANG Jing. Stress analysis of adhesively bonded single lap joint under eccentric load [J]. 吉林大学学报(工学版), 2016, 46(6): 1874-1880.
[8] YANG Hui-yan, HE Xiao-cong, ZHOU Sen. Simulation and calculation methods for clinched joint strength [J]. 吉林大学学报(工学版), 2015, 45(3): 864-871.
[9] ZHANG Qing,WANG Lei. Internal force analysis of multiple rows of piles based on differential equation set [J]. 吉林大学学报(工学版), 2014, 44(5): 1327-1333.
[10] ZHAO Shi-jia, XU Tao, CHEN Wei, TAN Li-hui. Efficient approach for modal sensitivity analysis for near defective systems [J]. 吉林大学学报(工学版), 2013, 43(增刊1): 497-499.
[11] XU Tao, ZHAO Shi-jia, ZHANG Wei, TAN Li-hui, LV Gang, LI Heng. Perturbed origin shift combined approximation method of N repeated defective systems [J]. 吉林大学学报(工学版), 2012, 42(增刊1): 147-150.
[12] YAN Guang, FAN Zhou, LI Zhong-hai, CHENG Xiao-quan, LIU Ke-ge, ZUO Chun-cheng. Analysis and design of composite cylindrical shell with cover [J]. , 2012, (06): 1437-1441.
[13] JIANG Hao, GUO Xue-dong. Concrete bridge modal parameter identification under seismic excitations [J]. 吉林大学学报(工学版), 2011, 41(增刊2): 185-188.
[14] TIAN Wei, GUO Xue-dong, YIN Xin-sheng. Theoretical and experimental research on oblique cross-section cracking resistance of wall-beam by concrete hollow block [J]. 吉林大学学报(工学版), 2011, 41(增刊2): 189-193.
[15] LI Chun-liang, WANG Guo-qiang, LIU Fu-shou, ZHAO Kai-jun. Mechanical behavior analysis of shield segment structure [J]. 吉林大学学报(工学版), 2011, 41(6): 1669-1674.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
Copyright © Journal of Jilin University(Engineering and Technology Edition), All Rights Reserved.
Tel: +86-431-85095297　Fax: +86-431-85094074　E-mail: xbgxb@jlu.edu.cn
Powered by Beijing Magtech Co. Ltd