Journal of Jilin University(Engineering and Technology Edition) ›› 2022, Vol. 52 ›› Issue (1): 46-52.doi: 10.13229/j.cnki.jdxbgxb20200502

Previous Articles     Next Articles

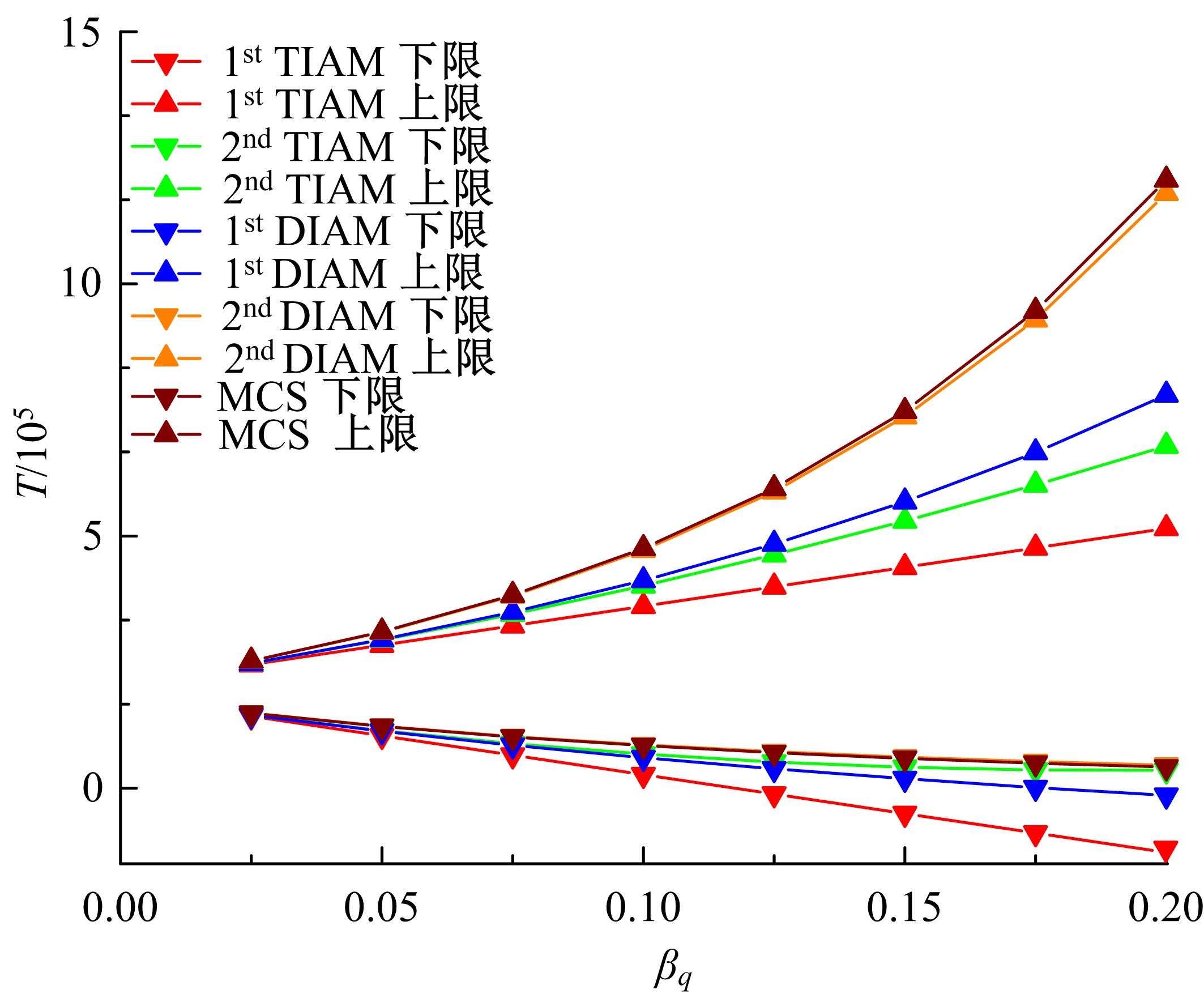
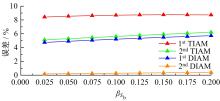
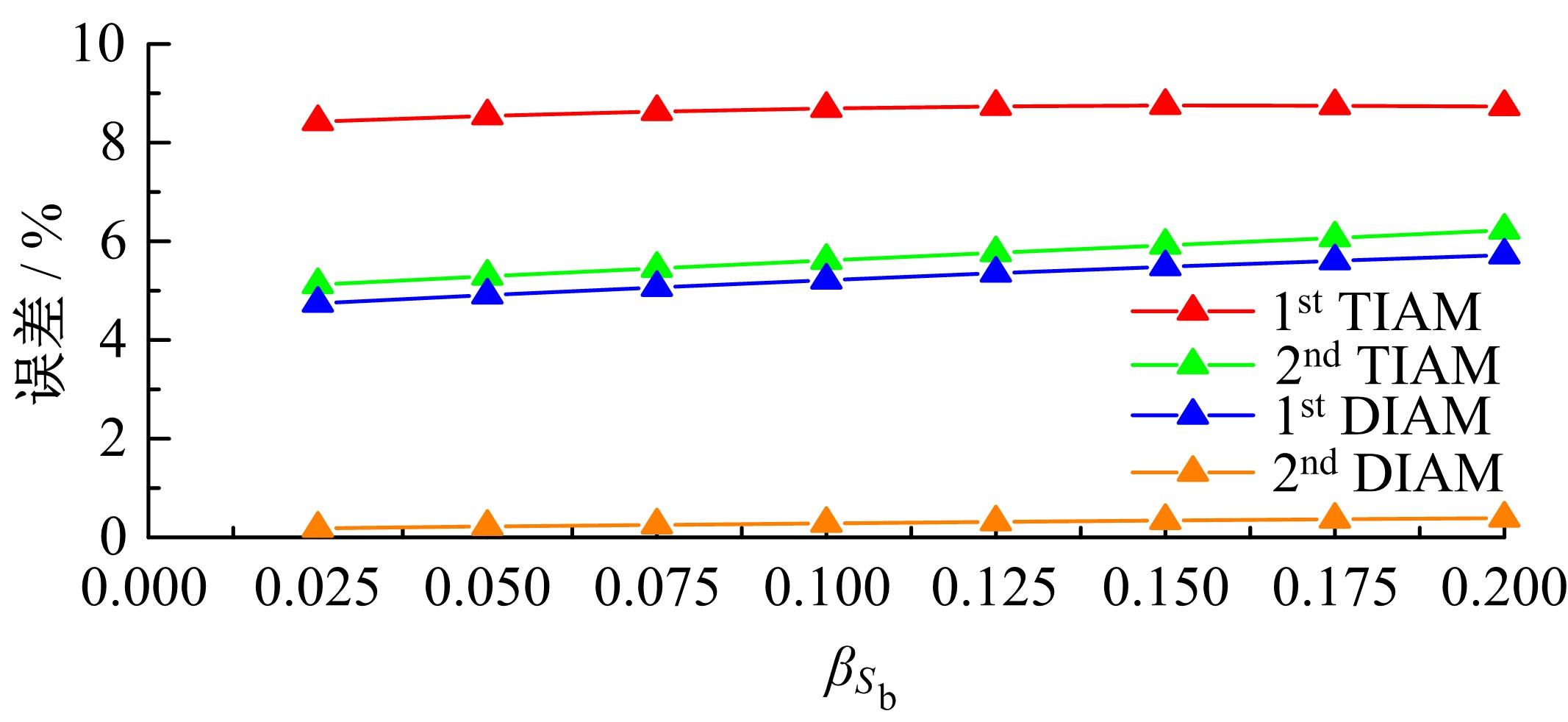
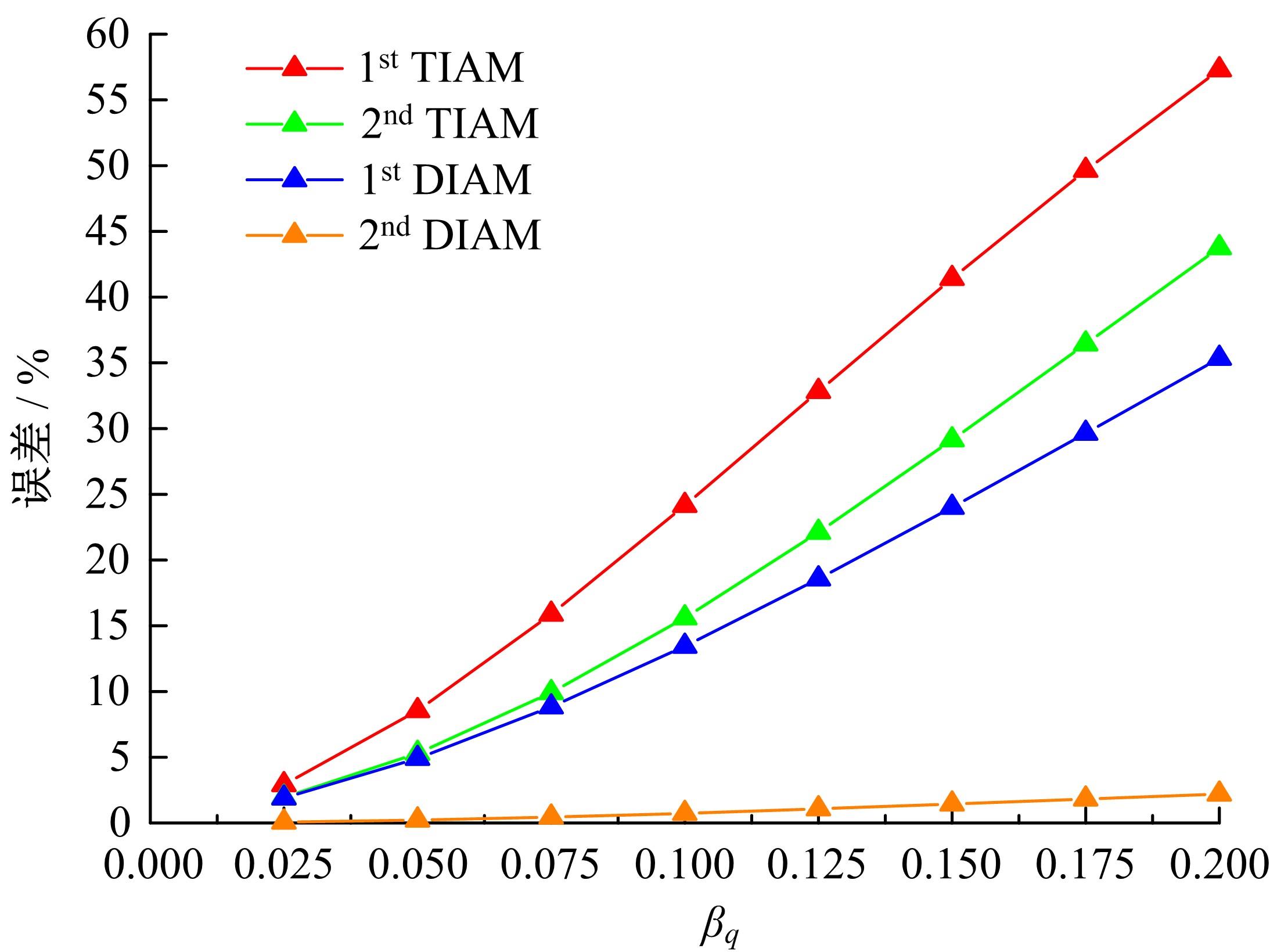
Interval analysis of structural fatigue life under random load

Guang-wei MENG1(),Chuan-xin REN2,Feng LI1(),Tong-hui WEI1   

  1. 1.School of Mechanical and Aerospace Engineering，Jilin University，Changchun 130022，China
    2.Institute of Optics and Electronics，Chinese Academy of Science，Chengdu 610041，China
  • Received:2020-06-07 Online:2022-01-01 Published:2022-01-14
  • Contact: Feng LI E-mail:mgw@jlu.edu.cn;fengli@jlu.edu.cn

RICH HTML

 1   

PDF (PC)

219

Abstract:

Traditional probabilistic methods require large number of samples to determine the probability density distribution of the dependent variable when analyzing the fatigue life of structures， and a small error in the probability density function will cause a large error in the fatigue life of the structure. To solve this problem， an interval analysis model for structural fatigue life under random loads were proposed. The uncertain factors that affect the fatigue life of the structure were regarded as interval variables. The dimensionality reduction expression of the fatigue life of the structure under random load was given. Combined with the interval mathematical method， the upper and lower limits of the fatigue life of the structure were obtained. Numerical examples show that compared with the Taylor method， the structural fatigue life interval analysis method based on dimensionality reduction algorithm proposed in this paper has higher accuracy. For the strength limit and fatigue parameters， the first-order dimensionality reduction algorithm has almost the same accuracy compared with the second-order Taylor method. For fatigue loads， when the variation range is large， the Taylor method cannot meet the accuracy requirements， but the second-order dimensionality reduction algorithm is still steady. It has high calculation accuracy and stability. Its calculation accuracy is roughly equivalent to genetic algorithm within a certain range， but the calculation efficiency is much higher than that of the genetic algorithm.

Key words: engineering mechanics, fatigue life, random load, interval analysis, dimensionality reduction algorithm, Taylor expansion

CLC Number: 

  • TP202.1

Fig.1

Structure diagram"

Fig.2

Load spectrum"

Fig.3

Comparison of fatigue life interval with βSb"

Fig.4

Comparison of fatigue life interval with βC"

Fig.5

Comparison of fatigue life interval with βq"

Fig.6

Comparison of error of upper limit of fatigue life varying with βSb"

Fig.7

Comparison of error of upper limit of fatigue life varying with βC"

Fig.8

Comparison of error of upper limit of fatigue life varying with βq"

Table 1

Comparison of calculation accuracy of fatigue life median"

βqMCS二阶降维算法遗传算法
中值/105中值/105误差/%中值/105误差/%
0.0252.0062.0050.02.0030.1
0.0502.1642.1620.12.1610.1
0.0752.4232.4190.22.4130.4
0.1002.8012.7900.42.7900.4
0.1253.3253.3020.73.2980.8
0.1504.0333.9921.04.0010.8
0.1754.9804.9091.44.9420.8
0.2006.2406.1261.86.1920.8
1 Karandikar J M, Kim N H, Schmitz T L. Prediction of remaining useful life for fatigue-damaged structures using Bayesian inference[J]. Engineering Fracture Mechanics, 2012, 96: 588-605.
2 Tsianika V, Geroulas V, Papadimitriou D, et al. A methodology of design for fatigue using an accelerated life testing approach with saddlepoint approximation[C]∥SAE International Paper, United States, 2019: 1-13.
3 李亚波, 宋清源, 杨凯, 等. 试样疲劳性能尺度效应的概率控制体积方法[J]. 力学学报, 2019, 51(5): 1363-1371.
Li Ya-bo, Song Qing-yuan, Yang Kai, et al. Probabilistic control volume method for the size effect of specimen fatigue performance [J]. Chinese Journal of Theoretical and Applied Mechanics, 2019, 51(5): 1363-1371.
4 孙祝岭. Birnbaum-Saunders疲劳寿命分布参数的回归估计方法[J]. 兵工学报, 2010, 31(9): 1259-1262.
Sun Zhu-ling. Regression estimation of the parameters of the Birnbaum-Saunders fatigue life distribution[J]. Acta Armamentarii, 2010, 31(9): 1259-1262.
5 Moore R E. Methods and Applications of Interval Analysis[M]. Philadephia: SIAML, 1979.
6 Long X Y, Jiang C, Liu K, et al. An interval analysis method for fatigue crack growth life prediction with uncertainty [J]. Computers and Structures, 2018, 210(2018): 1-11.
7 王军, 邱志平, 金延伟. 疲劳寿命的区间名义应力法及灵敏度分析[J]. 飞机设计, 2012, 32(6): 42-46.
Wang Jun, Qiu Zhi-ping, Jin Yan-wei. Nominal stress method of fatigue life and sensitivity analysis[J]. Aircraft Design, 2012, 32(6): 42-46.
8 陈小月, 文桂林, 刘杰,等. 基于泛灰数的结构疲劳寿命区间估计方法[J]. 计算机仿真, 2017, 34(4): 245-249.
Chen Xiao-yue, Wen Gui-lin, Liu Jie, et al. Estimation approach of structure fatigue life based on universal grey number[J]. Computer Simulation, 2017, 34(4): 245-249.
9 邱志平, 王晓军. 结构疲劳寿命的区间估计[J]. 力学学报, 2005(5): 653-657.
Qiu Zhi-ping, Wang Xiao-jun. Interval estimation for structural fatigue lifetime [J]. Chinese Journal of Theoretical and Applied Mechanics, 2005(5): 653-657.
10 孙作振, 孟广伟, 李锋, 等. 基于二阶区间摄动法的结构疲劳寿命估计[J]. 东北大学学报:自然科学版, 2013, 34(): 75-78.
Sun Zuo-zhen, Meng Guang-wei, Li Feng, et al. Structure fatigue life estimation based on the second-order interval perturbation method[J]. Journal of Northeastern University (Natural Science), 2013, 34(Sup.2): 75-78.
11 李锋, 孟广伟, 沙丽荣. 考虑模糊失效准则的结构疲劳寿命可靠性[J]. 航空学报, 2009, 30(12): 2316-2321.
Li Feng, Meng Guang-wei, Sha Li-rong. Reliability analysis of structural fatigue life under fuzzy failure criteria[J].Acta Aeronautica Et Astronautica Sinica, 2009, 30(12): 2316-2321.
12 Rahman S. A dimensional decomposition method for stochastic fracture mechanics[J]. Engineering Fracture Mechanics, 2006, 73(15): 2093-2109.
13 Li G, Zhang K. A combined reliability analysis approach with dimension reduction method and maximum entropy method[J]. Structural and Multidisciplinary Optimization, 2011, 43(1): 121-143.
14 付酥昇.ANSYS ncode designlife: 疲劳分析基础与实例教程[M].北京:人民邮电出版社, 2020.
15 Ponticelli G S, Guarino S, Giannini O. An optimal genetic algorithm for fatigue life control of medium carbon steel in laser hardening process[J]. Applied Sciences-Basel, 2020, 10(1401): 1-14.
16 闫楚良, 郝云霄, 刘克格. 基于遗传算法优化的BP神经网络的材料疲劳寿命预测[J]. 吉林大学学报:工学版, 2014, 44(6): 1710-1715.
Yan Chu-liang, Hao Yun-xiao, Liu Ke-ge. Fatigue life prediction of materials based on BP neural networks optimized by genetic algorithm[J]. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(6): 1710-1715.
[1] Yong PENG,Han-duo YANG,Xue-yuan LU,Yan-wei LI. Effect of void characteristics on virtual shear fatigue life of asphalt mixtures using discrete element method [J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(3): 956-964.
[2] Bi⁃xiong LI,Qiao LIAO,Yi⁃ping ZHANG,Lian ZHOU,Ping WEI,Kan LIU. Theoretical on flexural behavior of ultra high strength rebar reinforced engineered cementitious composites beam [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(4): 1153-1161.
[3] NI Ying-sheng,SUN Qi-xin,MA Ye,XU Dong,LIU Chao. Shear distribution of multi-cell corrugated steel web composite beams based on space grid analysis [J]. Journal of Jilin University(Engineering and Technology Edition), 2018, 48(6): 1735-1746.
[4] MAO Yu-ze, WANG Li-qin. Influence of squirrel-cage flexible support on the dynamic performance of ball bearing [J]. Journal of Jilin University(Engineering and Technology Edition), 2018, 48(5): 1508-1514.
[5] WANG Chun-sheng, ZOU Li, YANG Xin-hua. Analysis of fatigue life factors of aluminum alloy welded joints based on neighborhood rough set theory [J]. 吉林大学学报(工学版), 2017, 47(6): 1848-1853.
[6] YAN Ya-bin, WANG Xiao-yuan, WAN Qiang. Low-cycle fatigue fracture behavior of nanoscale interface [J]. 吉林大学学报(工学版), 2017, 47(4): 1201-1206.
[7] CHEN Jiang-yi, LIU Bao-yuan. Influence of fiber fracture damage on dispersion characteristic of guided wave in composite plate [J]. 吉林大学学报(工学版), 2017, 47(1): 180-184.
[8] MENG Guang-wei, FENG Xin-yu, ZHOU Li-ming, Li Feng. Structural reliability analysis based on dimension reduction algorithm [J]. 吉林大学学报(工学版), 2017, 47(1): 174-179.
[9] CAO Shan-shan, LEI Jun-qing. Fatigue life prediction of steel structure considering interval uncertainty [J]. 吉林大学学报(工学版), 2016, 46(3): 804-810.
[10] JIANG Rong-chao, WANG Deng-feng, QIN Min, JIANG Yong-feng. Lightweight design of twist beam of rear suspension of passenger car based on fatigue life [J]. 吉林大学学报(工学版), 2016, 46(1): 35-42.
[11] XING Bao-ying, HE Xiao-cong, WANG Yu-qi, DENG Cheng-jiang. Mechanism of mechanical properties of self-piercing riveted joints with multiple rivets [J]. 吉林大学学报(工学版), 2015, 45(5): 1488-1494.
[12] YANG Hui-yan, HE Xiao-cong, ZHOU Sen. Simulation and calculation methods for clinched joint strength [J]. 吉林大学学报(工学版), 2015, 45(3): 864-871.
[13] DENG Cheng-jiang, HE Xiao-cong, XING Bao-ying, WANG Yu-qi, ZENG Kai, DING Yan-fang. Mechanical properties of self-piercing riveted lap joints in dissimilar metal sheets of aluminum and copper [J]. 吉林大学学报(工学版), 2015, 45(2): 473-480.
[14] YAN Chu-liang, HAO Yun-xiao, LIU Ke-ge. Fatigue life prediction of materials based on BP neural networks optimized by genetic algorithm [J]. 吉林大学学报(工学版), 2014, 44(6): 1710-1715.
[15] ZHANG Qing,WANG Lei. Internal force analysis of multiple rows of piles based on differential equation set [J]. 吉林大学学报(工学版), 2014, 44(5): 1327-1333.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
Copyright © Journal of Jilin University(Engineering and Technology Edition), All Rights Reserved.
Tel: +86-431-85095297　Fax: +86-431-85094074　E-mail: xbgxb@jlu.edu.cn
Powered by Beijing Magtech Co. Ltd