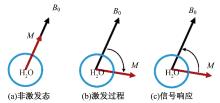
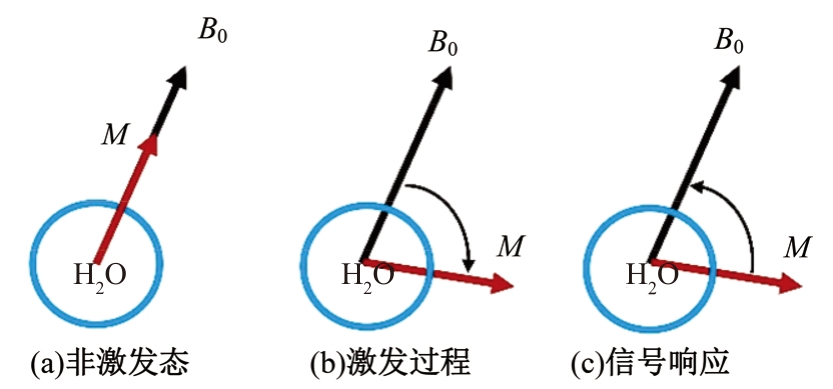
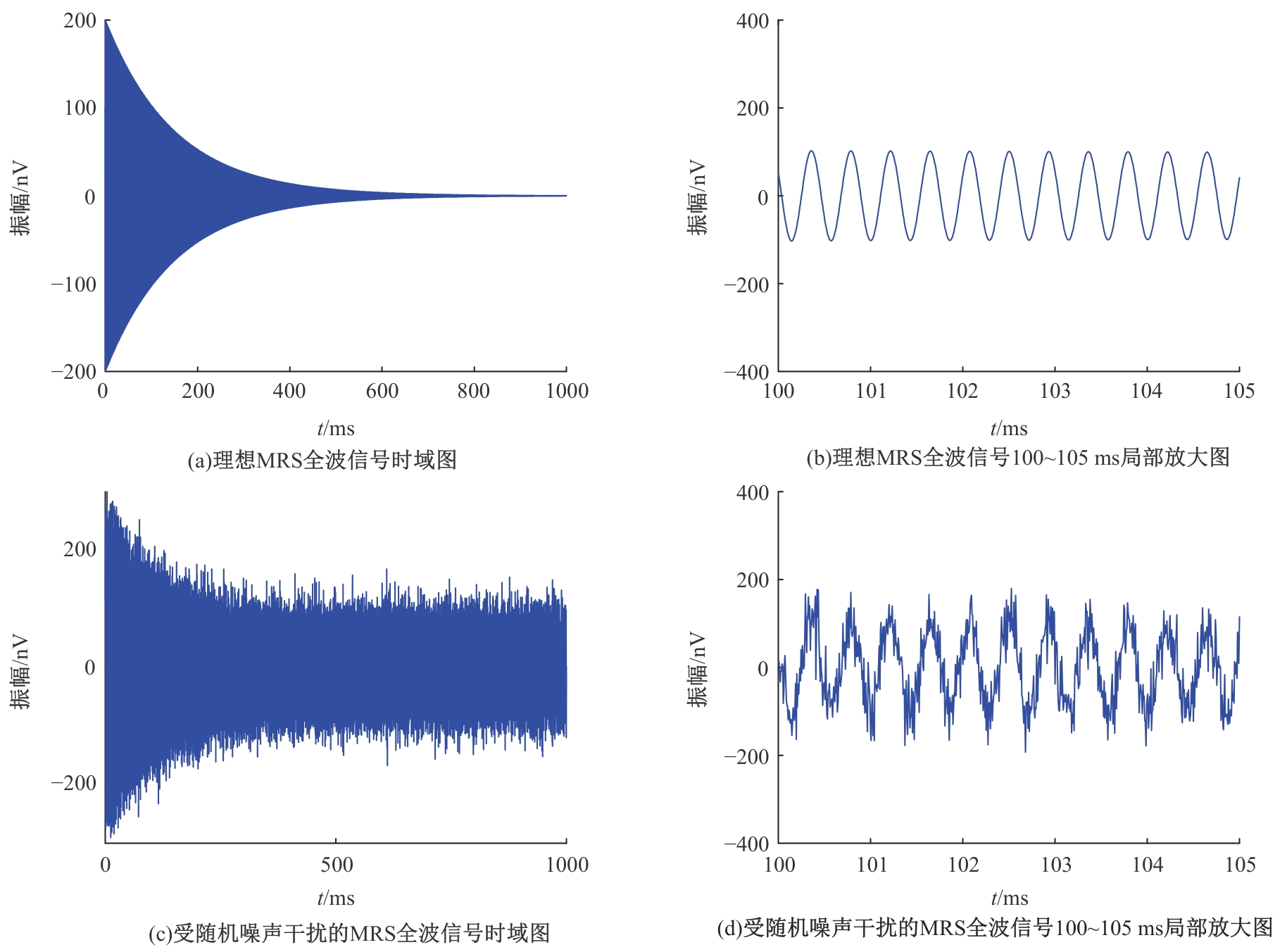
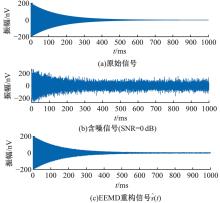
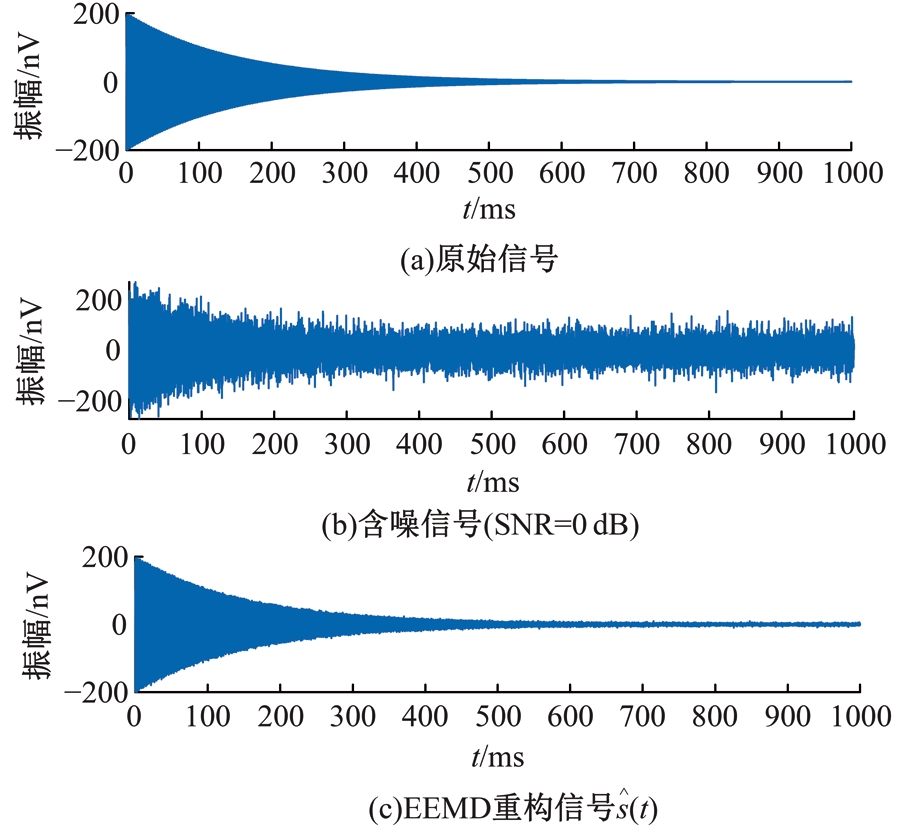
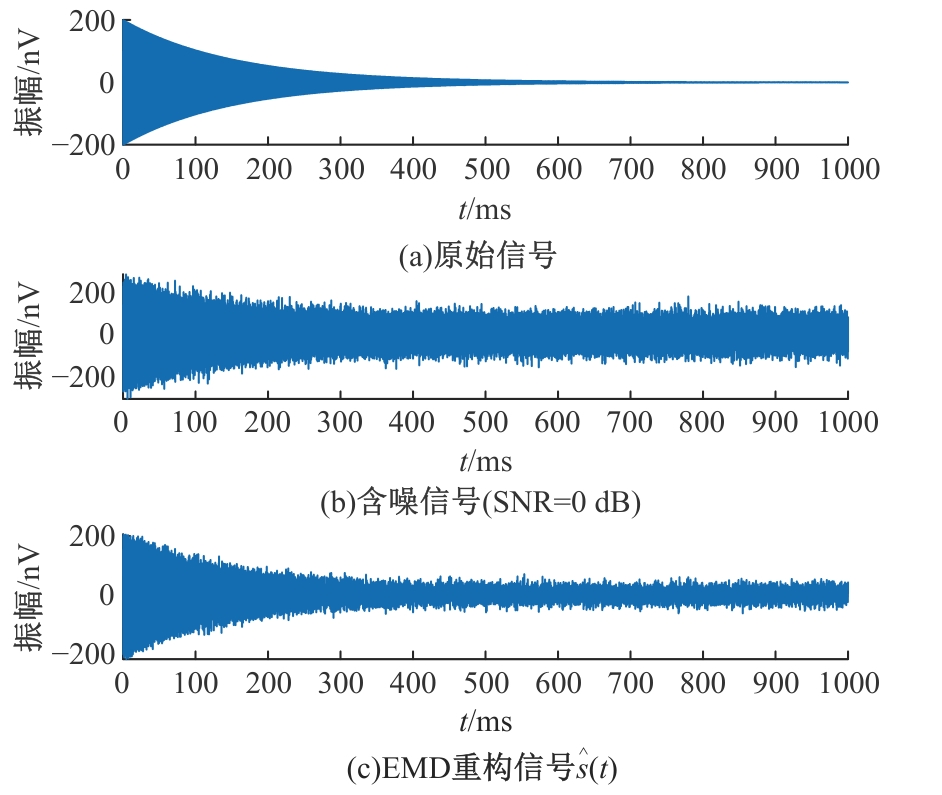
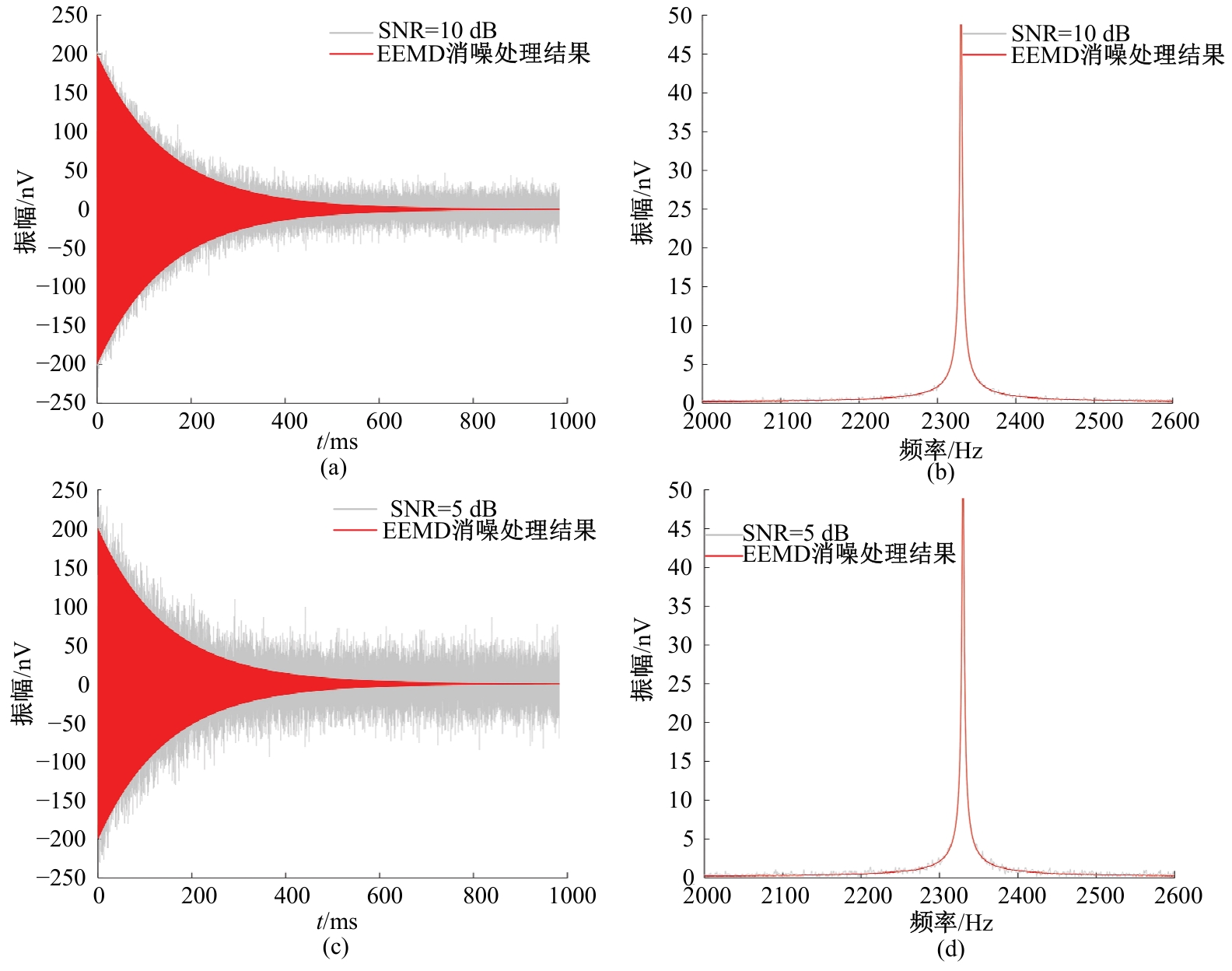
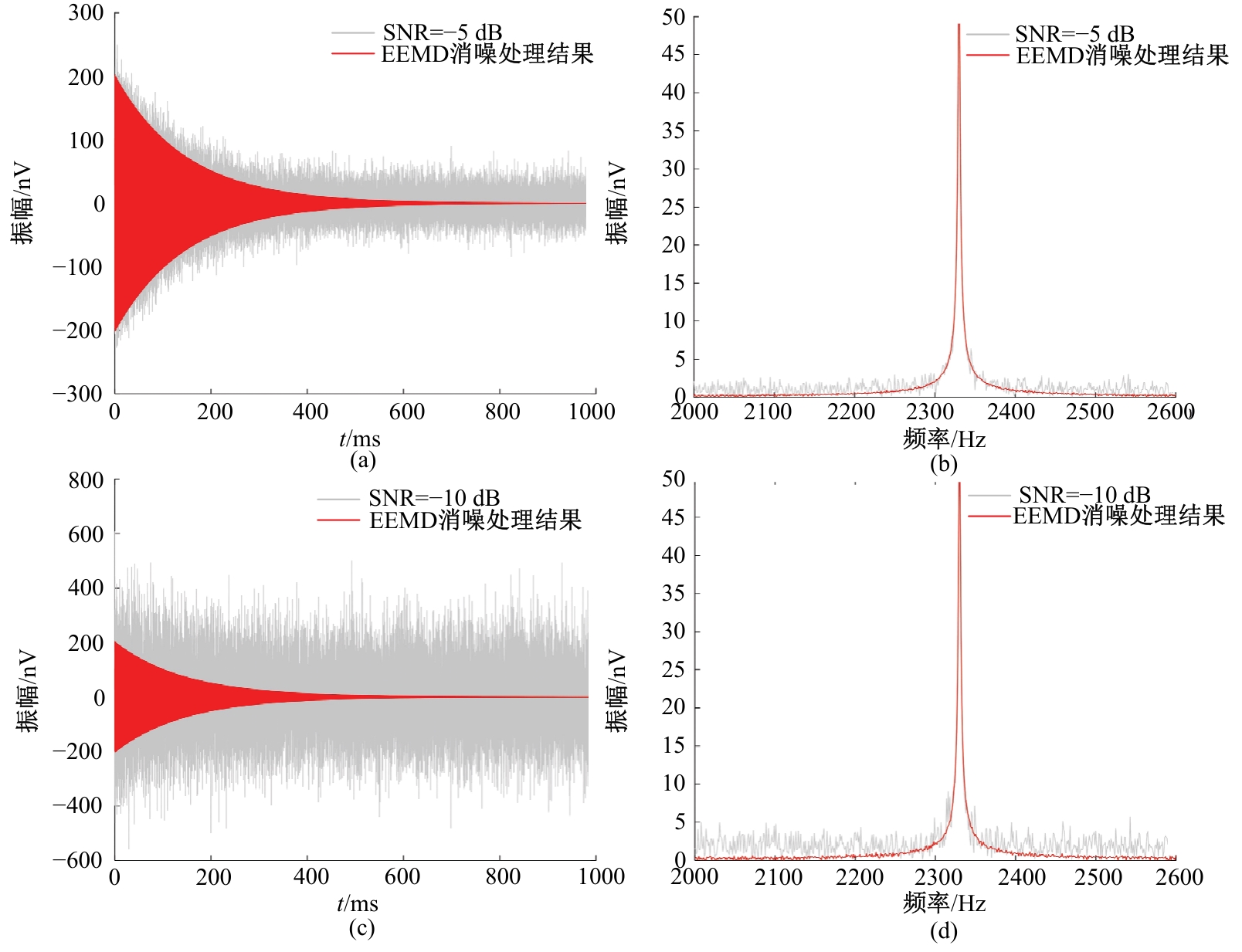
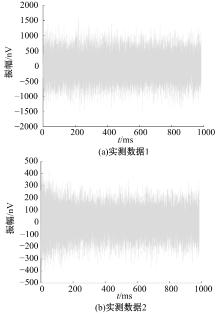
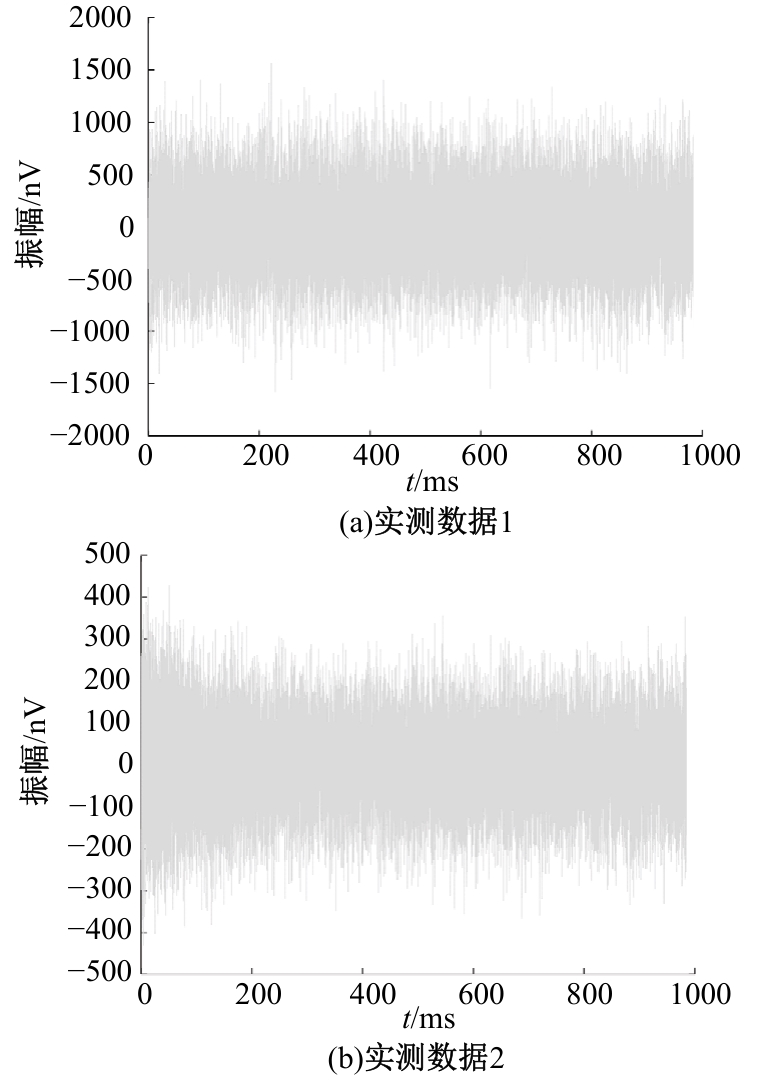
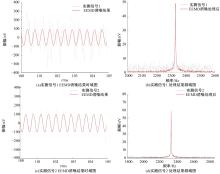
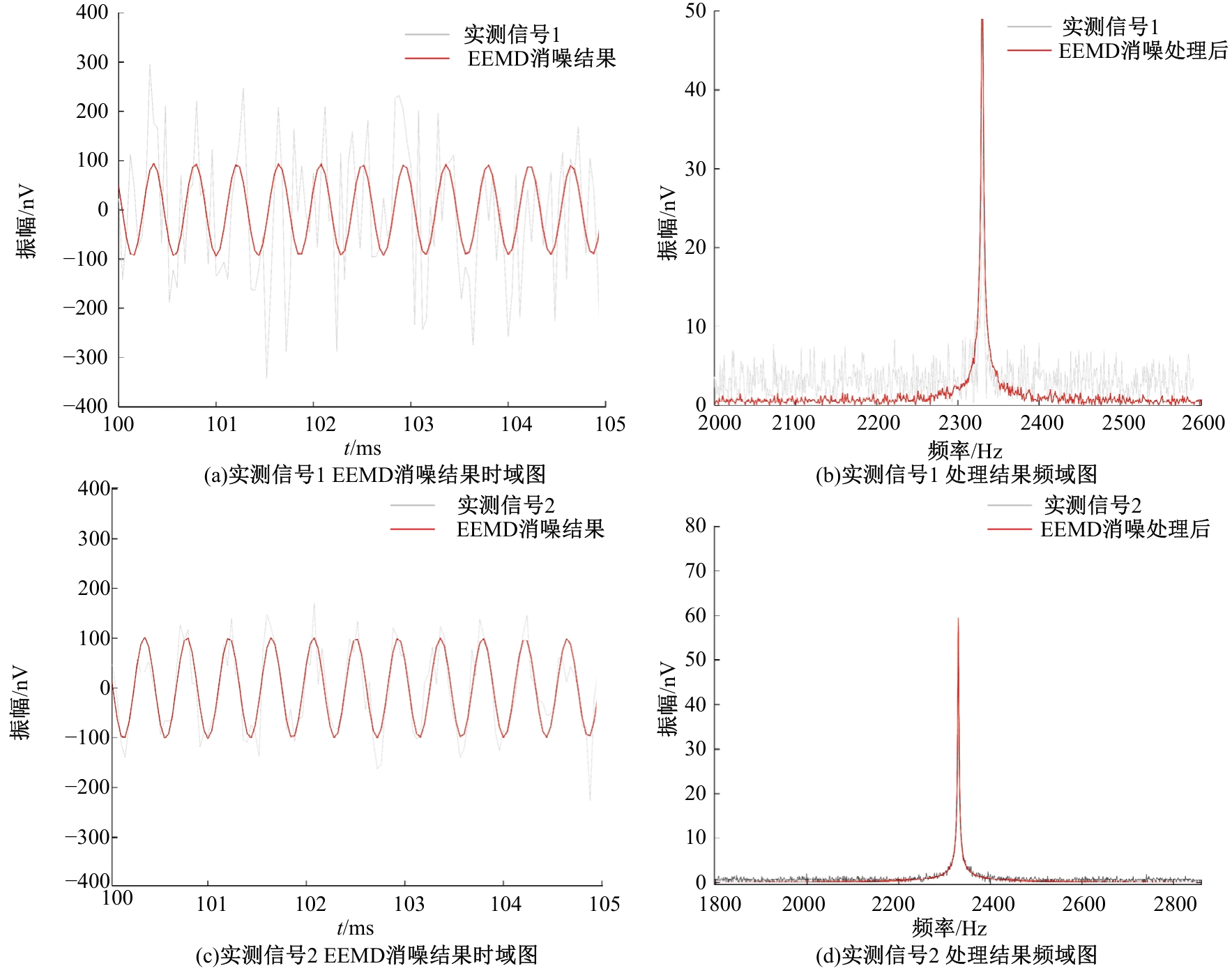
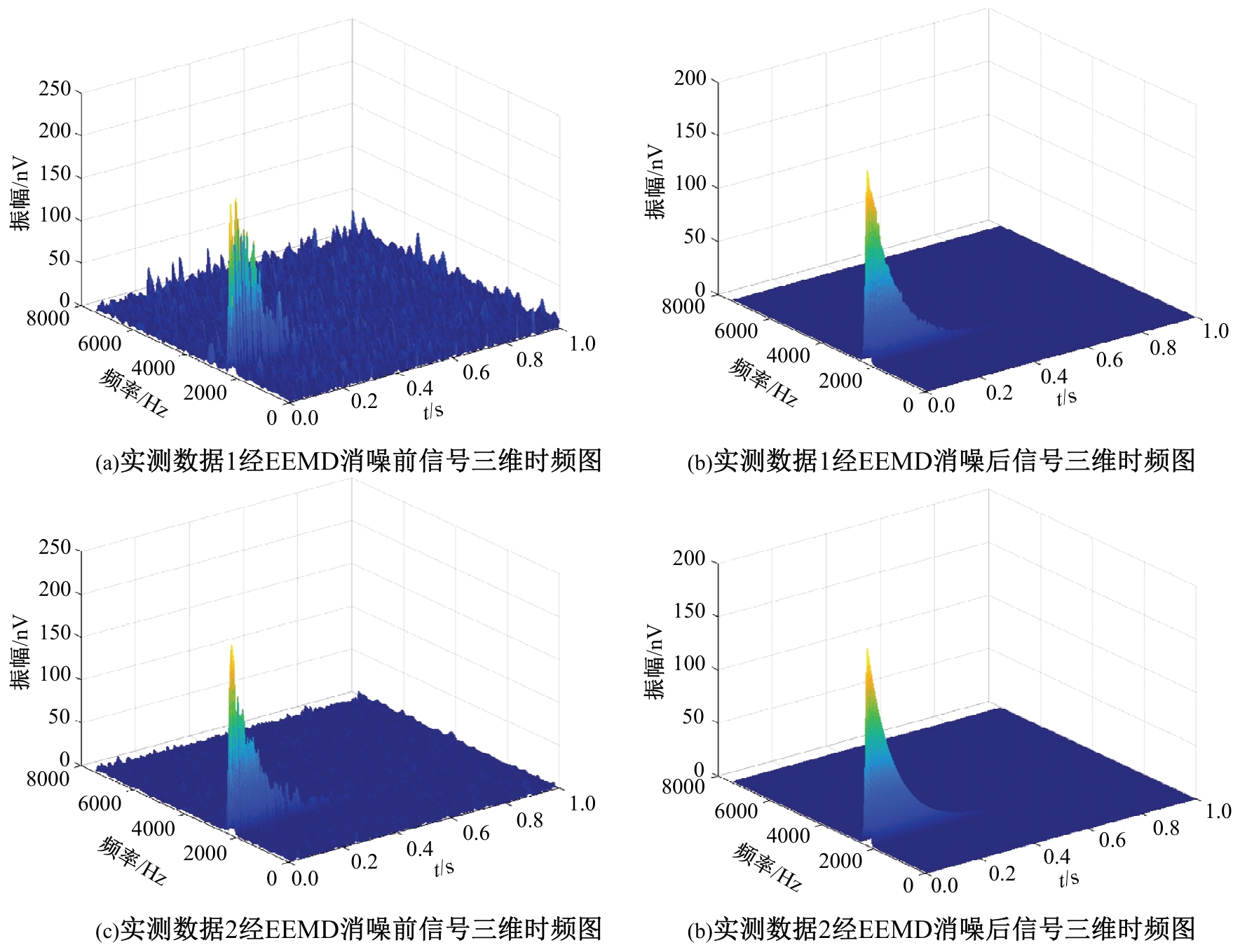
Journal of Jilin University(Engineering and Technology Edition) ›› 2025, Vol. 55 ›› Issue (8): 2771-2781.doi: 10.13229/j.cnki.jdxbgxb.20231282

Previous Articles    

Random noise suppression method for magnetic resonance full-wave signal with ensemble empirical mode decomposition

Ling WAN1,2(),Jia-lin ZHANG1,Shi-he LI1,Qing-yu PING1   

  1. 1.College of Instrumentation & Electrical Engineering，Jilin University，Changchun 130026，China
    2.Key Laboratory of Geo-Information Detection Instruments，Ministry of Education，Changchun 130026，China
  • Received:2023-11-20 Online:2025-08-01 Published:2025-11-14

RICH HTML

 0   

PDF (PC)

6

Abstract:

This article uses the ensemble empirical mode decomposition （EEMD） method to decompose and denoise the magnetic resonance full-wave signal， after obtaining a series of intrinsic mode function （IMF） components， the energy density and average period of each IMF component are calculated based on the principle of adaptive denoising，the IMF components dominated by noise are removed， and the selected IMF components are reconstructed，solved the problem of severe environmental noise interference in magnetic resonance full-wave signals. The simulation experimental data results show that when the signal-to-noise ratio of the magnetic resonance signal is as low as -10 dB， after EEMD processing， the magnetic resonance parameters can still be effectively extracted. The relative error of initial amplitude E0 extraction is 1.57%， the relative error of relaxation time T2* extraction is 2.96%， and the signal-to-noise ratio is improved to 10.31 dB. The noise suppression results of the measured data further validate the effectiveness and practicality of the algorithm studied in this paper， provides technical support for the application of magnetic resonance groundwater detection technology in complex roise environments.

Key words: ground magnetic resonance technology, magnetic resonance full-wave signal, ensemble empirical mode decomposition, random noise, data processing

CLC Number: 

  • TH763

Fig.1

Hydrogen proton magnetic resonance response model"

Fig.2

Simulated MRS full-wave signal"

Fig.3

Simulation data upper and lower envelope lines"

Fig.4

Simulated data mean signal"

Fig.5

MRS full-wave signal and signal s（t）containing random noise"

Fig.6

Decomposition diagram of simulation signal s（t） EEMD"

Table 1

RP j of IMF components obtained from EEMD decomposition"

IMF分量RP jIMF分量RP j
IMF10.724IMF70.791
IMF20.838IMF80.809
IMF30.852IMF90.863
IMF41.176IMF100.899
IMF52.528IMF110.834
IMF60.807IMF120.743

Fig.7

EEMD reconstruction signal diagram"

Table 2

RP j of IMF components obtained from EMD decomposition"

IMF分量RP jIMF分量RP j
IMF11.509IMF60.296
IMF20.175IMF70.271
IMF30.137IMF80.200
IMF40.069IMF90.596
IMF50.034res0.480

Fig.8

EMD reconstruction signal diagram"

Fig.9

Simulated MRS full-wave signal processing results with SNR=10 dB andSNR=5 dB"

Fig.10

Time-frequency map of simulated MRS full-wave signal processing results with SNR=-5dB andSNR=-10 dB"

Table 3

Signal parameter extraction results and signal-to-noise ratio of simulated signals with different signal-to-noise ratios after EEMD denoising processing"

仿真信号E0/nVfL/HzT2*/msSNR/dB
理想信号200.002 330.00150.00
SNR=10 dB200.912 330.01149.0332.587 2
SNR=5 dB200.012 330.03148.2827.443 8
SNR=0 dB202.192 330.03146.9523.138 6
SNR=-5 dB202.422 330.09146.2217.432 6
SNR=-10 dB203.172 329.98145.5610.316 7

Fig.11

Results of the measured data after noise processing"

Fig.12

Processing results of measured data"

Fig.13

3D time-frequency map of measured data processing results"

[1] Price W S. Spin dynamics: basics of nuclear magnetic resonance, 2nd edition[J]. Concepts in Magnetic Resonance Part A, 2009, 34A(1): 60-61.
[2] Dalgaard E, Christiansen P, Larsen J J, et al. A temporal and spatial analysis of anthropogenic noise sources affecting SNMR[J]. Journal of Applied Geophysics, 2014, 110: 34-42.
[3] Grunewald E, Grombacher D, Walsh D. Adiabatic pulses enhance surface nuclear magnetic resonance measurement and survey speed for groundwater investigations[J]. Geophysics, 2016, 81(4): 85-96.
[4] Lin T T, Zhang Y, Müller-Petke M. Random noise suppression of magnetic resonance sounding oscillating signal by combining empirical mode decomposition and time-frequency peak filtering[J]. IEEE Access, 2019, 7: 79917-79926.
[5] Li F, Li K T, Lu K, et al. Random noise suppression and parameter estimation for Magnetic Resonance Sounding signal based on maximum likelihood estimation[J]. Journal of Applied Geophysics, 2020, 176: No.104007.
[6] Lin T T, Yu S J, Wang P F, et al. Removal of a series of spikes from magnetic resonance sounding signal by combining empirical mode decomposition and wavelet thresholding[J]. Review of Scientific Instruments, 2022, 93(2): No.024502.
[7] Lin T T, Li Y, Lin Y S, et al. Magnetic resonance sounding signal extraction using the shaping-regularized Prony method[J]. Geophysical Journal International, 2022, 231(3): 2127-2143.
[8] 李丹丹. 基于集合经验模态分析的滚动轴承故障特征提取 [D].合肥: 安徽农业大学工学院, 2014.
Li Dan-dan. Rolling bearing fault feature extraction based on set empirical modal analysis[D]. Hefei: College of Engineering, Anhui Agricultural University, 2014.
[9] Behroozmand A A, Keating K, Auken E. A review of the principles and applications of the NMR technique for near-surface characterization[J]. Surveys in Geophysics, 2015, 36(1): 27-85.
[10] Chen L, Li X, Li X B, et al. Signal extraction using ensemble empirical mode decomposition and sparsity in pipeline magnetic flux leakage nondestructive evaluation[J]. Review of Scientific Instruments, 2009, 80(2): No.025105.
[11] Larsen J J. Model-based subtraction of spikes from surface nuclear magnetic resonance data[J]. Geophysics, 2016, 81(4): 1-8.
[12] Zheng J, Cheng J, Yang Y. Partly ensemble empirical mode decomposition: An improved noise-assisted method for eliminating mode mixing[J]. Signal Processing, 2014, 96: 362-374.
[13] Du S C, Liu T, Huang D L, et al. An optimal ensemble empirical mode decomposition method for vibration signal decomposition[J]. Journal of Vibration and Acoustics-Transactions of the Asme, 2017, 139(3): No.031003.
[14] Wang X X, Qi Y, Li Z, et al. A comparative study of DWT and EEMD methods for validation and correction of pyroshock data[J]. Journal of Aerospace Engineering, 2022, 35(5): No.0001458.
[15] Jiang Y, Tang C, Zhang X, et al. A novel rolling bearing defect detection method based on bispectrum analysis and cloud model-improved EEMD[J]. IEEE Access, 2020, 8: 24323-24333.
[16] 薛嫚. 总体平均经验模式分解法的理论研究 [D]. 哈尔滨: 哈尔滨工程大学水声工程学院, 2007.
Xue Man. Theoretical research on the decomposition method of overall average empirical mode[D]. Harbin: College of Underwater Acoustic Engineering, Harbin Engineering University, 2007.
[17] 李文志, 屈晓旭. 基于EEMD和共振峰的自适应语音去噪[J]. 现代电子技术, 2021, 44(23): 52-56.
Li Wen-zhi, Qu Xiao-xu. Adaptive speech denoising based on EEMD and resonance peaks[J]. Modern Electronic Technology, 2021, 44 (23): 52-56.
[18] 连雄飞. 基于改进经验模态分解的轴承故障诊断研究 [D]. 邯郸: 河北工程大学机械与装备工程学院, 2022.
Lian Xiong-fei. Research on bearing fault diagnosis based on improved empirical mode decomposition [D]. Handan: School of Mechanical and Equipment Engineering, Hebei University of Engineering, 2022.
[19] Kong Y L, Meng Y, Li W, et al. Satellite image time series decomposition based on EEMD[J]. Remote Sensing, 2015, 7(11): 15583-15604.
[20] Chang K M, Liu S H. Gaussian noise filtering from ECG by wiener filter and ensemble empirical mode decomposition[J]. Journal of Signal Processing Systems for Signal Image and Video Technology, 2011, 64(2): 249-264.
[21] 林婷婷, 李玥, 刘大震, 等. 基于频域对称法的磁共振数据残余噪声消除方法[J]. 中南大学学报: 自然科学版, 2021, 52(10): 3494-3504.
Lin Ting-ting, Li Yue, Liu Da-zhen, et al. Residual noise elimination method for magnetic resonance data based on frequency domain symmetry method[J]. Journal of Central South University (Natural Science Edition), 2021, 52 (10): 3494-3504.
[1] Wen-li JI,Zhong TIAN,Jing CHAI,Ding-ding ZHANG,Bin WANG. Prediction of water⁃flowing height in fractured zone based on distributed optical fiber and multi⁃attribute fusion [J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(4): 1200-1210.
[2] Li-na LI,Xiao-hui WEI,Lin-lin HAO,Xing-wang WANG,Chu WANG. Cost⁃effective elastic resource allocation strategy in large⁃scale streaming data processing [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(5): 1832-1843.
[3] Bo-xin WANG,Hai-tao YANG,Qing WANG,Xin GAO,Xiao-xu CHEN. Bridge vibration signal optimization filtering method based on improved CEEMD⁃multi⁃scale permutation entropy analysis [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(1): 216-226.
[4] WEI Xiao-hui, LIU Zhi-liang, ZHUANG Yuan, LI Hong-liang, LI Xiang. Adaptive checkpoint mechanism supporting large-scale stream data processing [J]. 吉林大学学报(工学版), 2017, 47(1): 199-207.
[5] TIAN Ya-nan, LI Yue, LIN Hong-bo, XU Xue-chun. Frequency-domain regularized Wiener filtering for seismic random noise suppression [J]. 吉林大学学报(工学版), 2015, 45(6): 2043-2048.
[6] JIANG Wan-lu,LU Chuan-qi,ZHU Yong. HHT and fuzzy C-means clustering-based fault recognition for axial piston pump [J]. 吉林大学学报(工学版), 2015, 45(2): 429-436.
[7] ZHANG Jie, LI Yue. Reduction of random noise in seismic data by parallel radial-trace time-frequency peak filtering [J]. 吉林大学学报(工学版), 2014, 44(3): 882-887.
[8] LIN Hong-bo, LI Yue, ZHANG Chao, MA Hai-tao. Based on fuzzy multi-level time-frequency peak filtering attenuation of seismic random noise [J]. 吉林大学学报(工学版), 2013, 43(增刊1): 410-413.
[9] WU Yong-zhi, LIU Yi-sheng, WAN Qiu-hua, DING Lin-hui. Dynamic interpolation error measuring system for high precision optical encoder [J]. 吉林大学学报(工学版), 2012, 42(增刊1): 309-313.
[10] QUAN Yong, LUYi-Na, HUANG Yong-Ping, LI Wen-Hui, ZHANG Zhen-Hua, ZHOU Bin. Resampling of pointbased models [J]. 吉林大学学报(工学版), 2010, 40(增刊): 315-0319.
[11] Quan Yong，Li Wen-hui，Lu Yi-nan，Zhang Zhen-hua . New method for simplification of 3D scattered points [J]. 吉林大学学报(工学版), 2008, 38(增刊): 156-0162.
[12] GANG Long-hui, JIANG Gui-yan, ZHANG Xiao-dong, WANG Jiang-feng. Screening and checking for ITS traffic sensor data [J]. 吉林大学学报(工学版), 2004, (1): 122-126.
[13] CAI Zhong-yi, SUN Xi-hong, LI Ming-zhe, FENG Zhao-hua. Smoothing-finite element method for representation and differentiation of discrete experimental data [J]. 吉林大学学报(工学版), 2003, (2): 64-68.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
Copyright © Journal of Jilin University(Engineering and Technology Edition), All Rights Reserved.
Tel: +86-431-85095297　Fax: +86-431-85094074　E-mail: xbgxb@jlu.edu.cn
Powered by Beijing Magtech Co. Ltd