Journal of Jilin University(Engineering and Technology Edition) ›› 2020, Vol. 50 ›› Issue (1): 216-226.doi: 10.13229/j.cnki.jdxbgxb20190013

Previous Articles    

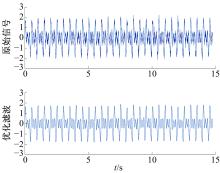
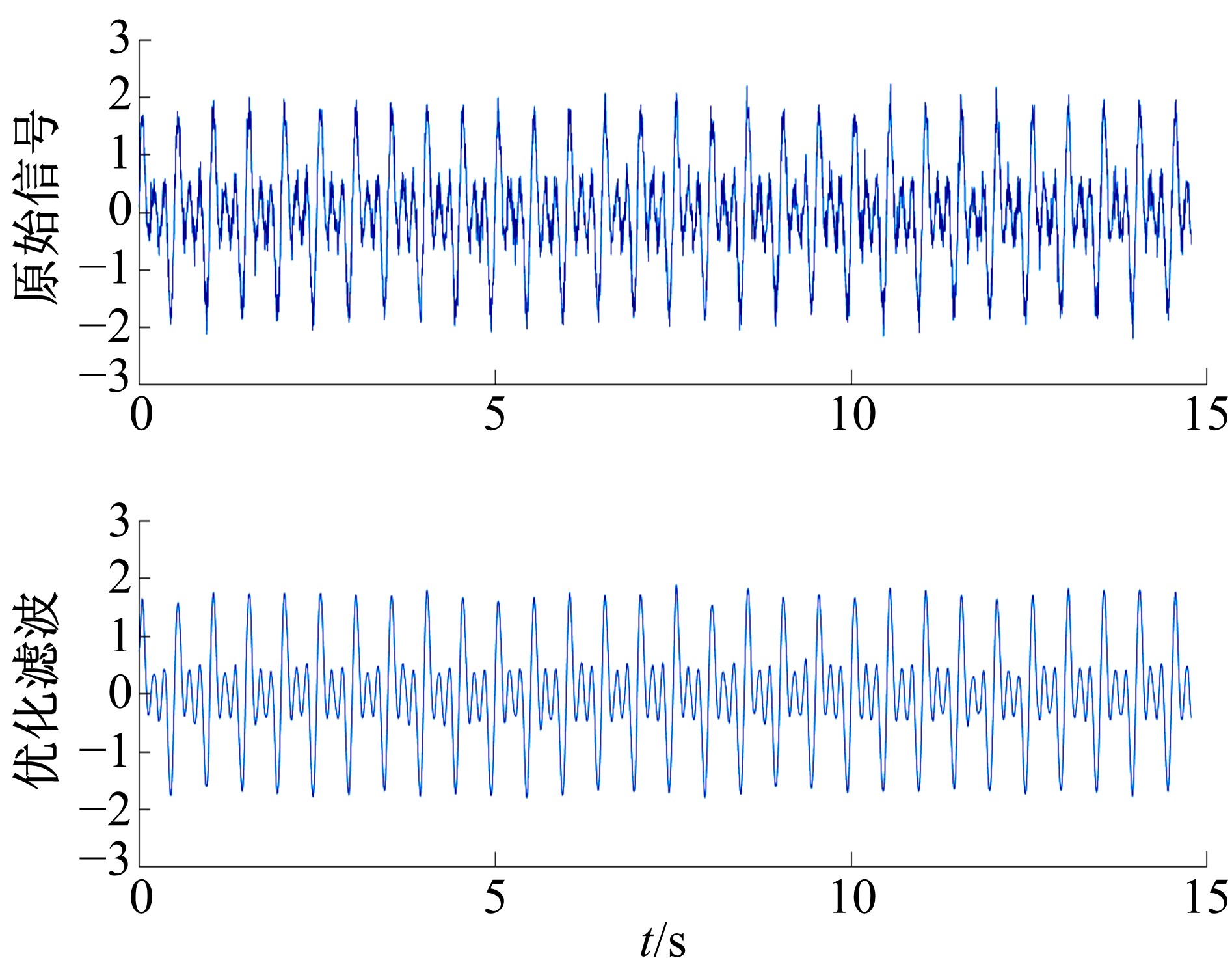
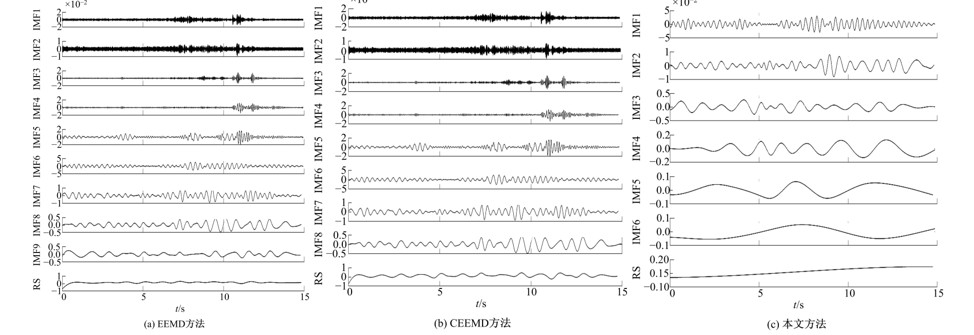
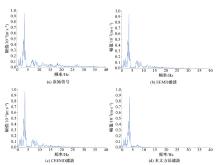
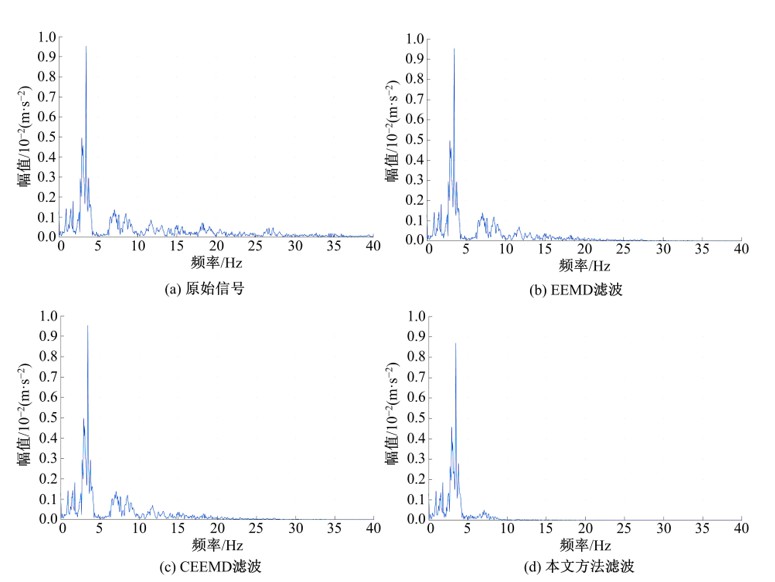
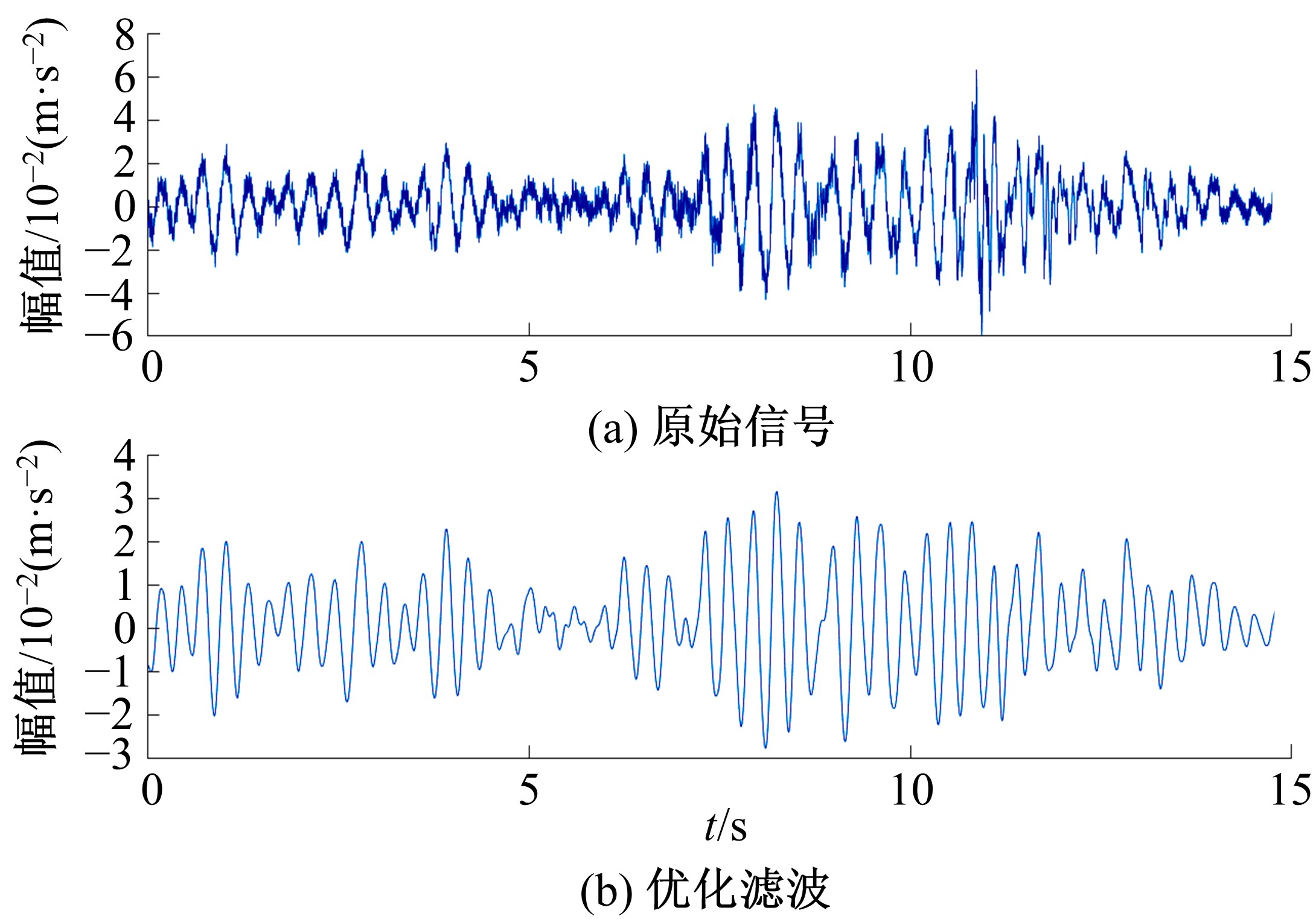
Bridge vibration signal optimization filtering method based on improved CEEMD⁃multi⁃scale permutation entropy analysis

Bo-xin WANG1(),Hai-tao YANG1,Qing WANG1,Xin GAO1(),Xiao-xu CHEN2   

  1. 1. College of Construction Engineering, Jilin University, Changchun 130021, China
    2. Changchun Smart City Science and Technology Co. Ltd. , Changchun 130033, China
  • Received:2019-01-04 Online:2020-01-01 Published:2020-02-06
  • Contact: Xin GAO E-mail:boxinwang@jlu.edu.cn;gao_xin@jlu.edu.cn

RICH HTML

 3   

PDF (PC)

178

Abstract:

To solve the problem of bridge vibration signal with high degree of non-stationary feature, an optimization filtering method of adaptive decomposition and reconstruction is proposed for the bridge health monitoring. On the basis of complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN), the original signal is decomposed into multiple intrinsic mode functions (IMFs) with different feature time-scales. The endpoint mirroring method is used to suppress endpoint effect. In order to find the IMFs with high randomness, the multi-scale permutation entropy (MPE) is introduced to analyze the mean entropy value of each IMF at different scales. Then the noise component and abnormal component are respectively eliminated to complete the first filtering. In order to achieve better similarity and smoothness for the final filter, the optimized reconstruction model is established to complete the second filtering. The research shows that adaptive decomposition stage of the proposed method has better completeness, orthogonality and computational efficiency than traditional ensemble empirical mode decomposition (EEMD) and complementary ensemble empirical mode decomposition (CEEMD) methods. Meanwhile, the proposed method suppresses the mode mixing phenomenon to a certain extent, and the endpoint effect is improved. Through the optimized reconstruction, the final filter signal has high signal-to-noise ratio. Finally, the measured signal analysis once again proves the advantages of the proposed method, the filter result can be used as the basis of bridge health monitoring technology.

Key words: bridge engineering, bridge health monitoring, decomposition and reconstruction, filtering, complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN)

CLC Number: 

  • U448.27

Fig.1

"

Fig.2

Simulated signal"

Table 1

Simulated signal basic condition setting"

方 法 加噪次数 加噪幅值 迭代次数
EEMD 200 0.2 100
CEEMD 100(对)×2 0.2 100
本文 200 0.2 100

Fig.3

"

Fig.4

MPE mean value distribution in each IMF"

Fig.5

Final decomposition of proposed method"

Table 2

EEMD decomposition IMF correlation analysis"

s1 s2 s3
IMF1 -0.002 5 -0.001 5 0.003 7
IMF2 -0.001 3 0.000 2 0.002 7
IMF3 0.004 1 0.008 2 0.019 3
IMF4 0.005 5 0.106 9 0.896 3
IMF5 -0.058 4 0.397 7 0.894 7
IMF6 0.243 9 0.937 4 0.019 6
IMF7 0.983 0 0.023 4 0.015 6
IMF8 0.320 9 0.021 3 0.019 2
IMF9 0.054 9 0.028 1 0.019 5
RS 0.088 6 0.045 1 0.030 1

Table 3

CEEMD decomposition IMF correlation analysis"

s1 s2 s3
IMF1 -0.001 9 -0.001 9 0.003 4
IMF2 -0.001 2 -0.000 3 0.002 8
IMF3 0.006 0 0.011 0 0.018 3
IMF4 0.002 7 0.098 0 0.907 6
IMF5 -0.065 3 0.431 5 0.877 8
IMF6 0.287 2 0.921 9 0.018 8
IMF7 0.981 4 0.019 7 0.014 2
IMF8 0.311 1 0.023 3 0.019 8
RS 0.102 9 0.052 3 0.035 2

Table 4

Proposed method decomposition IMF correlation analysis"

s1 s2 s3
IMF1 0.069 7 0.473 6 0.861 3
IMF2 0.098 4 0.953 4 0.001 9
IMF3 0.972 5 0.027 3 0.024 1
IMF4 0.049 0 0.022 8 0.014 8
IMF5 0.032 5 0.016 0 0.010 6
IMF6 0.033 4 0.016 6 0.011 1
RS 0.032 4 0.016 2 0.010 8

Fig.6

"

Table 5

Evaluation indicators for different methods"

方 法 Mse t/s Ort
EEMD 0.003 3 324.5855 0.216 8
CEEMD 0.002 8 294.0562 0.222 4
本文 4.103 8×10-5 50.1826 0.103 5

Table 6

Filter signal analysis of proposed method"

相似度 光滑度 目标函数
LB 1 0.419 2 0.007 0 0.997 3
LB 2 0.350 3 0.007 0 0.917 1
LB 3 0.190 3 0.007 1 0.727 0
LB 4 0.189 3 0.007 1 0.725 8
LB 5 0.187 2 0.007 1 0.723 3
LB 6 0.187 3 0.007 1 0.723 4
LB 7 0.185 8 0.007 1 0.721 7

Fig.7

Simulation signal optimization filter"

Table 7

Real signal basic condition setting"

方法 加噪次数 加噪幅值 迭代次数
EEMD 300 0.2 200
CEEMD 150(对)×2 0.2 200
本文 300 0.2 200

Fig.8

Real signal decomposition results for each method"

Table 8

Evaluation indicators for each methods"

方 法 t /s Ort dnSNR
EEMD 936.8431 0.2184 9.1537
CEEMD 880.8714 0.2135 9.1488
本文方法 82.9216 0.0063 6.0958

Fig.9

Unilateral spectrum of each method filters"

Fig.10

Comparison between original signal and optimized filter of proposed method"

1 Huang N E , Shen Z , Long S R , et al . The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceeding of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995.
2 Gai G H . The processing of rotor startup signals based on empirical mode decomposition[J]. Mechanical Systems and Signal Processing, 2006, 20(1): 222-235.
3 Huang N E , Shen Z , Long S R . A new view of non-linear water waves: the hilbert spectrum[J]. Annual Review of Fluid Mechanics, 1999, 31(1): 417-457.
4 Wu Z H , Huang N E , Chen X Y . The multi-dimensional ensemble empirical mode decomposition method[J]. Advances in Adaptive Data Analysis, 2009, 1(3): 339-472.
5 Wu Z H , Huang N E . Ensemble empirical mode decomposition:a noise assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41.
6 Yeh J R , Shieh J S , Huang N E . Complementary ensemble empirical mode decomposition: a novel noise enhanced data analysis method[J]. Advances in Adaptive Data Analysis, 2010, 2(2): 135-156.
7 Huang N E , Wu M , Long S R , et al . A confidence limit for the empirical mode decomposition and Hilbert spectral analysis[J]. Proceedings of the Royal Society A, 2003, 459: 2317-2345.
8 刘薇娜, 周小龙, 姜振海, 等 . 基于最优特征的改进经验模态分解方法[J]. 吉林大学学报：工学版, 2017, 47(6): 1957-1963.
Liu Wei-na , Zhou Xiao-long , Jiang Zhen-hai , et al . Improved empirical mode decomposition method based on optimal features[J]. Journal of Jilin University(Engineering and Technology Edition), 2017, 47(6): 1957-1963.
9 吴琛, 项洪, 杜喜朋 . 基于数据/极值联合对称延拓的端点效应处理及其应用[J]. 振动与冲击, 2017, 36(22): 178-184.
Wu Chen , Xiang Hong , Du Xi-peng . A process method for end effects of HHT based on data/extrema symmetrical extension and its application[J]. Journal of Vibration and Shock, 2017, 36(22): 178-184.
10 刘慧婷, 张旻, 程家兴 . 基于多项式拟合算法的EMD端点问题的处理[J]. 计算机工程与应用, 2004, 40(16): 84-86, 100.
Liu Hui-ting , Zhang Min , Cheng Jia-xing . Dealing with the end issue of EMD based on polynomial fitting algorithm[J]. Computer Engineering and Applications, 2004, 40(16): 84-86, 100.
11 徐健, 周志祥, 赵丽娜 . 基于AEEMD和改进DATA-SSI算法桥梁结构模态参数自动化识别[J]. 土木工程学报, 2017, 50(7): 87-98.
Xu Jian , Zhou Zhi-xiang , Zhao Li-na . Automatic identification of modal parameter for bridges based on AEEMD and improved DATA-SSI[J]. China Civil Engineering Journal, 2017, 50(7): 87-98.
12 陈永高, 钟振宇 . 基于CEEMD分解和DATA-SSI算法的斜拉桥模态参数识别[J]. 振动与冲击, 2016, 35(8): 166-172, 200.
Chen Yong-gao , Zhong Zhen-yu . Modal parameter identification of a cable-stayed bridge based on CEEMD and DATA-SSI algorithm[J]. Journal of Vibration and Shock, 2016, 35(8): 166-172, 200.
13 单德山, 李乔, 黄珍 . 桥梁动力测试信号的自适应分解与重构[J]. 振动与冲击, 2015, 34(3): 1-6, 13.
Shan De-shan , Li Qiao , Huang Zhen . Adaptive decomposition and reconstruction for bridge dynamic testing signals[J]. Journal of Vibration and Shock, 2015, 34(3): 1-6, 13.
14 郑近德, 程军圣, 杨宇 . 改进的EEMD算法及其应用研究[J]. 振动与冲击, 2013, 32(21): 21-26, 46.
Zheng Jin-de , Cheng Jun-sheng , Yang Yu . Modified EEMD algorithm and its applications[J]. Journal of Vibration and Shock, 2013, 32(21): 21-26, 46.
15 胡显能, 蔡改贫, 罗小燕, 等 . 基于CEEMDAN和多尺度排列熵的球磨机负荷识别方法[J]. 噪声与振动控制, 2018, 38(3): 146-151.
Hu Xian-neng , Cai Gai-pin , Luo Xiao-yan , et al . Load identification method for ball mills based on CEEMDAN and multi-scale permutation entropy[J]. Noise and Vibration Control, 2018, 38(3): 146-151.
16 Bandt C , Pompe B . Permutation entropy: a natural complexity measure for time series[J]. Physical Review Letters, The American Physiological Society, 2002, 88(17): 174102.
17 姚文坡, 刘铁兵, 戴加飞, 等 . 脑电信号的多尺度排列熵分析[J]. 物理学报, 2014, 63(7): 078704.
Yao Wen-po , Liu Tie-bing , Dai Jia-fei , et al . Multiscale permutation entropy analysis of electro encephalogram[J]. Acta Physica Sinica, 2014, 63(7): 078704.
[1] Miao ZHANG,Yong-jiu QIAN,Fang ZHANG,Shou-qin ZHU. Experimental analysis of spatial force performance of concrete-reinforced stone arch bridge based on enlarged section method [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(1): 210-215.
[2] Yi JIA,Ren-da ZHAO,Yong-bao WANG,Fu-hai LI. Sensitivity analysis of viscous damper parameters for multi⁃span and long⁃unit continuous girder bridges [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(6): 1871-1883.
[3] En-ze LIU,Wen-fu WU. Monochrome fruit growth detection internet architecture based oncomprehensive indicator quality evaluation algorithm [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(6): 2019-2026.
[4] Chun-ling ZHONG,Dong LIANG,Yun-long ZHANG,Jing WANG. Calculation of natural vibration frequency of simply supported beam strengthened by external prestressing [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(6): 1884-1890.
[5] Lun-hua BAI,Rui-li SHEN,Xing-biao ZHANG,Lu WANG. In-plane stability of self-anchored suspension bridge [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(5): 1500-1508.
[6] Jin⁃gang ZHAO,Ming ZHANG,Yu⁃lin ZHAN,Ming⁃zhi XIE. Damage criterion of reinforced concrete pier based on plastic strain energy density [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(4): 1124-1133.
[7] Shi⁃cheng WAN,Qiao HUANG,Jian GUAN,Zhao⁃yuan GUO. Strengthening of continuous steel⁃concrete composite beams in negative moment region using prestressed carbon fiber⁃reinforced polymer plates [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(4): 1114-1123.
[8] Jing LI,Qiu⁃jun SHI,Peng LIU,Ya⁃wei HU. Neural network sliding mode control of commercial vehicle ABS based on longitudinal vehicle speed estimation [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(4): 1017-1025.
[9] Wan⁃heng LI,Lin SHEN,Shao⁃peng WANG,Shang⁃chuan ZHAO. Damage assessment of bridge construction based onmulti⁃stage subregion mobile test [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(3): 773-780.
[10] Tohtonur,Hai⁃long ZHANG,Jie WANG,Na WANG,Xin⁃chen YE,Wan⁃qiong WANG. High speed median filtering algorithm based on graphics processing unit [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(3): 979-985.
[11] HUI Ying-xin,MAO Ming-jie,LIU Hai-feng,ZHANG Shang-rong. Influence of structural seismic response of bridges crossing active fault [J]. Journal of Jilin University(Engineering and Technology Edition), 2018, 48(6): 1725-1734.
[12] LIU Yuan-ning, LIU Shuai, ZHU Xiao-dong, CHEN Yi-hao, ZHENG Shao-ge, SHEN Chun-zhuang. LOG operator and adaptive optimization Gabor filtering for iris recognition [J]. Journal of Jilin University(Engineering and Technology Edition), 2018, 48(5): 1606-1613.
[13] LIU Shu, JIANG Qi-gang, ZHU Hang, LI Xiao-dong. Reconstruction of Landsat NDVI time series of Xianghai natural deserve based on a hybrid filtering algorithm Hyb-F [J]. 吉林大学学报(工学版), 2018, 48(3): 957-967.
[14] ZHENG Yi-feng, ZHAO Qun, BAO Wei, LI Zhuang, YU Xiao-fei. Wind resistance performance of long-span continuous rigid-frame bridge in cantilever construction stage [J]. 吉林大学学报(工学版), 2018, 48(2): 466-472.
[15] GONG Ya-feng, HE Yu-long, TAN Guo-jin, SHEN Yang-fan. Anti-overturning stability analysis for three-span continuous curved girder bridge with single column pier [J]. 吉林大学学报(工学版), 2018, 48(1): 133-140.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
Copyright © Journal of Jilin University(Engineering and Technology Edition), All Rights Reserved.
Tel: +86-431-85095297　Fax: +86-431-85094074　E-mail: xbgxb@jlu.edu.cn
Powered by Beijing Magtech Co. Ltd