叶锦华(1982),男,博士研究生.研究方向:机器人技术.E-mail:jinhuayea@gmail.com
针对包含执行器动力学模型的三阶不确定非完整轮式移动机器人系统,提出了一种基于反演设计和双强化学习自适应模糊系统的轨迹跟踪控制方法。该控制方法对运动学控制器采用分流控制技术,防止系统运行初期的速度跳变。对本体动力学和执行器动力学分别使用强化学习自适应模糊控制,优化补偿常规方法难以解决的系统未知参数和非参数不确定性,并利用鲁棒项来消除未知外部扰动和模糊控制逼近误差对系统的影响,提高了系统的控制性能。Lyapunov理论证明:控制系统是稳定且最终有界收敛的,仿真结果表明了该方法的有效性。
A trajectory tracking method is proposed for three-order uncertain nonholonomic mobile robot with actuator dynamic model. This method is based on the backstepping technique and dual reinforcement learning adaptive fuzzy logic system. The shunting control technique is used to prevent the velocity jump at the beginning of system for the motion controller. The reinforcement learning adaptive fuzzy logic control is employed for both body dynamics and actuator dynamics, such that the unknown system uncertainties of parameters and non-parameters can be compensated optimally. Moreover, in order to enhance the control performance, the robust compensators are applied to eliminate the impact of unknown external disturbance and approximation error of fuzzy system. The stability and ultimately bounded convergence of the control system are proven by Lyapunov theory. The validity of this method is verified by the simulation results.
非完整轮式移动机器人(NWMR)作为典型的非完整系统,其控制问题一直受到广泛关注。由于不满足Brockett的必要条件[ 1],常规光滑时不变控制方法不再适用,加上其本身是一个MIMO耦合的非线性系统,因此,对此类系统的控制变得特别困难。实际系统不可避免地存在模型不确定性,并受到未知外部扰动的影响,此时如何保证NWMR仍然能够进行精确的轨迹跟踪,国内外学者对此提出了诸多解决方法,主要有鲁棒控制[ 2, 3]、自适应控制[ 4, 5]和智能控制[ 6, 7]等方法。其中,鲁棒控制往往需要知道系统不确定的上界,自适应控制则更适用于固定或慢时变的结构参数不确定性,具备逼近未知不确定性函数能力的智能控制尽管解决了上述不足,然而对于具有高度不确定因素的系统,控制效果有限。此外,现有的NWMR轨迹跟踪控制方法中,尽管已经考虑了系统动力学对系统的影响,却较少考虑执行器动力学对系统的影响,这在高速、高精的应用场合中,将导致系统跟踪控制性能下降,而控制器输出直接为执行器控制量,更符合实际情况。另外,由系统运行初期初始误差较大而引起的速度跳变将导致很大的控制量,这对于受到机构和执行器限制的实际系统是难以实现的。
为了解决上述问题,本文综合考虑了NWMR的运动学、本体动力学和执行器动力学几方面,结合反演设计技术,提出了一种双强化学习自适应模糊控制(RLAFC)方法,解决了系统包含复杂未知不确定因素的NWMR轨迹跟踪控制问题,并通过鲁棒项来消除系统扰动和模糊控制逼近误差的影响,还利用基于仿生神经动力学的分流控制技术[ 8],解决了系统运行初期的速度跳变问题。RLAFC[ 9]不仅具备自适应模糊控制优化逼近任意不确定函数的能力,还利用强化学习方法对自适应参数向量进行进一步优化,加快了RLAFC的收敛速度,并使得控制系统能够适应未知模型信息少或未知参数大范围变化等传统方法难以消除的不确定性,解决了常规智能控制的不足,提高了系统的适应性和鲁棒性。
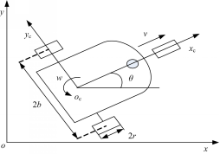
研究对象为如图1所示的(2,0)型[ 10]NWMR,两轮间的距离为2b,轮子半径为r,质心o c为两轮轴线的中心,NWMR整车质量为m,绕通过o c点轴线的转动惯量为I。
定义质心o c点在全局坐标系xoy下的位姿为: q=[ x, y, θ]T则根据理想非完整约束条件,其运动学模型为[ 11]:
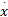

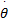
式中: v为 NWMR的前进速度; w为 NWMR的转动角速度。
使用拉格朗日乘子法,可建立 NWMR从 oc输出的动力学模型为[ 11]:
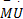

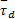
式中: τ=[τv,τw ]T为 NWMR的前进驱动力矩和转动驱动力矩; U=[ v, w]T,标称值矩阵 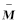

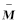
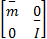


Ψ1=Δ 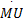
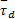
文中假设NWMR两轮采用特性相同的独立直流电机驱动,则NWMR执行器动力学模型为[ 12]:
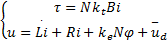 | (3) |
式中:N为电机输出端到轮子的减速比;kt为电机力矩常数; L、 R分别为电机电感和内阻; ke为反电动势常数; i为电机的励磁电流; 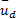
B= 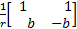
u=[ur,ul ]T为两轮驱动电机的控制电压输入; φ=[φr,φl ]T为两轮转速,满足:
φ= JU= 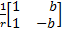
根据式(3)(4)可知控制力矩 τ与控制电压 u的动态关系式为:
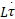
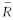

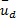
式中: Ψ2=Δ 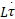
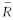

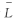
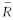

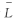
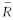
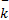
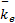
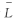
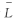
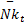
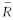
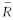
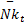

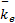
为了降低设计复杂度,文中结合反演设计思想,对系统的运动学(式(1)),本体动力学(式(2))和执行器动力学(式(3))3个子系统分别进行控制器设计。反演设计方法将复杂的非线性系统分解成不超过系统阶数的子系统,然后与普适性强的 Lyapunov理论结合,为每个子系统设计辅助控制器,前一个子系统的辅助控制器作为控制目标集成到下一个子系统的控制器中去,并在最后一步完成总体控制器的设计。文中控制器设计分3个步骤进行。
(1)设计运动学辅助控制器 Uc
定义时变参考轨迹位姿: qr= 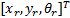
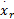
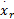
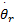
式中: vr、 wr为期望参考速度值。
定义 NWMR的轨迹跟踪误差为:
ec=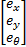 = = 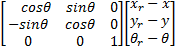 | (7) |
则轨迹跟踪误差动态方程为:
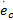 = = 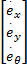 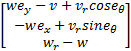 | (8) |
运动学轨迹跟踪是设计一个合理的辅助速度控制器 Uc= 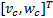
Uc=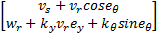 | (9) |
式中: k y >0, k θ >0,有界 vs为与引起速度跳变变量相关的辅助信号,其动态更新表达式为:
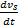
式中: A为 vs的无源衰减率; B1、 B2分别为 vc的设计上界和下界值;上界门限线性函数 g1( e x)和下界门限线性函数 g2( e x)分别设计为:
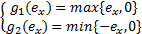 | (11) |
通过门限线性函数的切换,基于式(10)由系统误差 e x引起的速度跳变将被限制在[ -B2, B1]内。定义速度跟踪误差 e U= 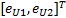
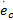 = = 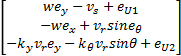 | (12) |
(2)设计本体动力学辅助控制器 τc
第(2)步的设计目标是以 Uc为参考输入,设计辅助力矩控制器 τc= 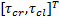
τc= kp e U+ 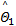
式中: kp=diag( κp, κp), κp为正的常数;设计鲁棒补偿项 γ1为:
γ1=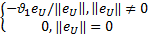 | (14) |
式中:ϑ1为正的常数;自适应模糊补偿项 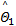
Θ1( U, 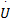
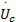
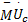

式中: e v= 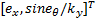
Θ1= 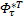
式中: ω1为模糊系统的逼近误差; ξ τ为模糊基向量; 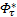
用估计值 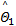
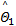
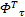
为了获得接近最优的参数向量,文中参数向量通过强化学习自适应方法进行更新,更新律为:
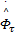 = Γ τ ξ τ = Γ τ ξ τ 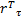 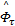 | (18) |
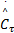 =- Γ τc‖ e U‖ ξ τ =- Γ τc‖ e U‖ ξ τ 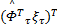 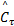 | (19) |
式中: Γ τ=diag( ν τ, ν τ); Γ τc=diag( ν τc, ν τc); ν τ、 ν τc、 η τ为正的常数;强化学习信号 r τ取:
r τ= e U+‖ e U‖ 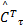
定义力矩跟踪误差 e T= 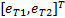
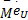

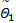
式中: 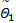
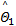
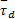
(3)设计执行器控制器 u
以第(2)步力矩控制输出 τc为参考输入,第(3)步是设计电压控制输入 u,来消除误差 e T,进一步考虑实际执行器存在饱和问题,取 u为:
u= k I D I+ k v D v+ 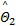
式中: k I=diag( κ I, κ I); k v=diag( κ v, κ v);
D I= 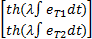
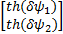
滤波跟踪误差 ψ= 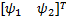
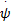
β=diag( κ ψ, κ ψ); λ、 δ、 α、 κ I、 κ v和 κ ψ为正的常数;符号th(·)等价于饱和函数tanh(·)。设计鲁棒补偿项 γ2为:
γ2=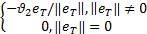 | (24) |
式中:ϑ2为正的常数。
与第(2)步设计相似,利用自适应模糊估计值 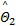
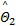
Θ2( τ, 
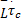
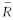

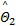
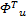
取参数向量估计 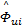
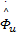 = Γ u ξ u = Γ u ξ u 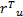 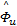 | (27) |
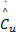 =- Γ uc‖ e T‖ ξ u =- Γ uc‖ e T‖ ξ u 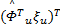 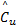 | (28) |
r u= e T+‖ e T‖ 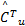
式中: Γ u=diag( ν u); Γ uc=diag( ν uc, ν uc); ν u、 ν uc、 η u为正的常数。
将式(22)代入式(5)有:
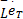
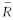
式中: Θ2= Θ2- 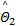
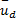
根据上述设计步骤,有如下定理成立:
定理1 给定系统(1),(2),(5),选择运动学控制器(9)、本体动力学控制器(13)、执行器动力学控制器(22),分流模型(10)和参数强化学习自适应律(18) ~(20)、(27) ~(29),则闭环控制系统可实现最终有界稳定轨迹跟踪。
证明 选择如下总体 Lyapunov函数
L=L1 +L2 +L3(31)
式中:
L1= 
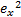
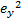
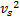
L2= 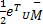

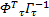

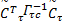
L3=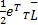 e T+ e T+  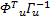  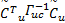 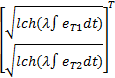 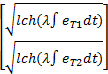 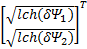 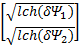 | (34) |
式中: Λ=diag( λ); Δ=diag( δ);符号lch(·)与符号ln(cosh(·))等价。令 B1 =B2 =B,对 L1求导,并将式(9)(10)(12)代入求导后的 L1可得:
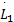
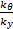
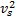
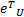
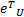
对于NWMR本体动力学系统有如下性质:
性质1 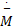

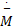

将式(18) ~(21)代入求导后的 L2,并结合性质1有:
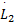
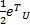
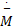

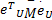
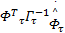
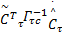
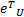
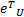
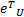
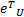
式中:
F1=‖ e U‖tr{= 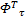
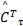
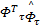
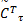
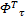
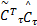
定义: D1=- k I D I- k v D v;
D2=2 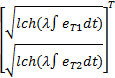
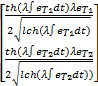
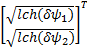
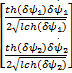
V2 =α ψT k v 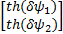
将式(27) ~(30)代入求导后的 L3,得到:
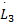
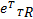
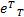
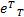
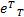
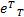
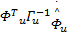
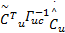
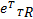
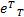
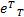
式中:
F2=‖ e T‖tr{= 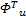
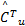
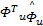
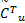
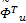
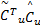
为了方便下一步分析,进行如下假设:
假设1 ‖ ρ1‖≤ Ξ1,‖ ρ2‖≤ Ξ2, Ξ1 >0, Ξ2 >0。
将式(14)(24)(35)(36)(38)代入求导后的式(31),再结合假设1,当取 ϑ i≥ Ξ i, i=1,2,有:
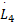
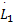
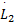
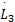
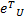
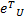
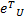
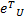
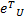
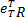
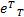
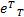
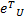
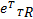
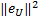
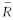
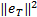
式中:λmin( kp)、 λmin( 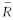
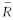
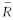
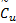
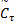
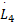
注1 通过增大 λmin( kp), e U可收敛于任意小值,而当‖ e T‖
注2 文中控制器采用质心输出,而非轮子输出,并用强化学习自适应模糊系统逼近包含了系统本体动力学和执行器动力学结构参数矩阵的不确定项,这使得文中控制器可适用于同类型(如(2,1)型[ 10])的其他非完整轮式移动机器人系统的轨迹跟踪控制。
通过 Matlab软件来验证文中方法的可行性,移动机器人本体的物理参数为: 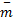
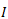
执行器的物理参数为:N=21, 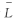
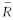
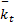
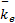
本体动力学不确定项为: Ψ1=(10sin( t-8) +e -t,10cos( t-8)=2 e -t)。
电机动力学的不确定项为: Ψ2=(sin(2 t)=2cos( t-2),2sin( t-2)=cos(3 t)),
扰动项 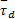
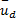
运动学控制器参数取: k y=8, k θ=10, A=2, B=4。本体动力学控制器参数取: κ p=80, ϑ1=25。电机动力学控制器参数取: κ I=0 .6, κ v=2, α=6; κ ψ=8, λ=10, δ=10, ϑ2=10。
模糊系统、逻辑系统使用如下模糊推理规则:
R l:如果 X j为 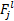
式中: j为模糊系统输入变量个数; l为模糊规则数,为了减少计算量,提高系统的实时性,文中每个变量使用3个与模糊规则相对应的高斯隶属度函数, RLAFC的参数为: ν τ=28, ν τc=20, ν u=6, ν uc=4, η τ =η u=1。
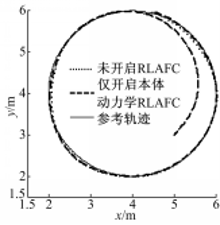
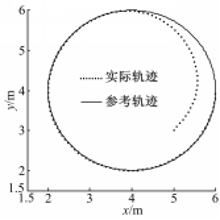
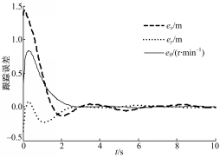
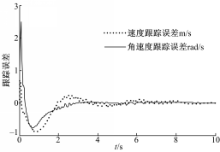
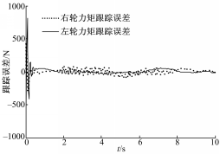
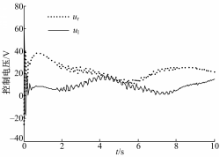
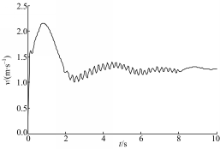
首先进行圆轨迹跟踪试验,轨迹参数为: Ur=[2π/5,π/5]T, qr(0)=[6,4, π/2]T, NWMR的初始参数为: q(0)=[5,3, π/3]T, U(0)=[0,0]T,在关闭 RLAFC和仅开启本体动力学 RLAFC的情况下进行轨迹跟踪控制,仿真结果如图2所示,可见执行器动力学不确定性对系统有着不可忽略的影响,实际应用应给予考虑。应用文中双 RLAFC控制器的轨迹跟踪仿真结果如图3 ~图8所示。从图3可以看出:控制器同时消除了本体动力学、执行器动力学不确定性和外部扰动的影响,保证NWMR精确地跟踪参考轨迹。图4~图6表明3个子系统的跟踪误差都收敛于有界范围,达到了反演控制的目标。图7描述了执行器控制输入的变化情况,可见通过饱和约束使得控制量处于合理范围,而由于使用分流控制技术,图8所示的NWMR移动速度变化初期过渡平稳,未发生跳变现象。
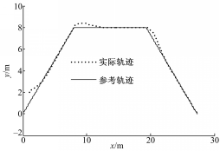
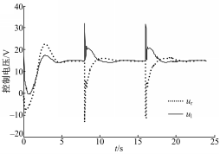
再进行分段直线轨迹跟踪,轨迹参数取: Ur=[1 .414,0]T, qr(0)=[0,0, π/4]T,第2段和第3段直线参数为: θr | t=8 s=0, θr | t=16 s =-π/4, NWMR的初始位姿为: q(0)=[1,2, π/3]T,试验结果如图9和图10所示。从图9可以看出对于分段直线,在过渡处误差明显加大,但控制器使得系统跟踪误差迅速减小, NWMR很快重新实现对参考轨迹的渐进跟踪,跟踪效果良好。而尽管过渡处的控制输入变化较为剧烈,如图10所示,其幅度依然处在合理范围内。
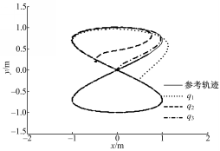
最后进行多个初始位姿的8字形轨迹跟踪,轨迹参数: xr=sin( t/3), yr=sin( t/6), qr(0)=[0,0,0 .4634]T, NWMR初始位姿分别为: q1=[0.5,-0.2,π/4]T, q2=[-0.5,0.2,π]T, q3=[0,0,π/2]T,跟踪情况如图11所示,结果表明了文中控制器具有半全局性,且对于变曲率复杂曲线也具有良好的控制效果。
NWMR的执行器动力学对控制器性能有着不可忽略的影响,当考虑执行器动力学时,NWMR为三阶系统,加大了控制器的设计难度,而通过反演设计有效地降低了控制系统的设计复杂度,文中提出的带鲁棒项的双RLAFC,提高了系统的收敛效率,并保证了NWMR在本体动力学系统和执行器动力学系统同时存在复杂不确定性和未知外界扰动时能够实现精确的轨迹跟踪。控制器结合基于仿生神经动力学的分流控制技术使得系统能在较大初始偏差时不发生常规控制器的速度跳变。对圆弧轨迹、分段直线轨迹和多个初始位姿的8字型曲线的仿真试验结果表明:文中控制策略使得系统是最终有界收敛的,并可以有效地消除系统复杂不确定性的影响,抑制外部扰动,提高NWMR的轨迹跟踪效果。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|