基于可穿戴传感系统的人体肢段定位动态评估

引用本文

刘坤, 韩宣, 刘政. 基于可穿戴传感系统的人体肢段定位动态评估. 2014, 44(4): 1016-1023
[LIU Kun, HAN Xuan, LIU Zheng. Ambulatory assessment of human segmental orientation using accelerometers. Journal of Jilin University Engineering and Technology Edition, 2014, 44(4): 1016-1023] 复制到剪切板

Permissions

基于可穿戴传感系统的人体肢段定位动态评估

刘坤, 韩宣, 刘政

吉林大学机械科学与工程学院,长春130022

作者简介：刘坤（1981-）,男,副教授,博士.研究方向:下肢智能康复训练设备.E-mail:kunliu@jlu.edu.cn

基金:国家自然科学基金青年基金项目(81101138); 中国博士后科学基金项目(2011M500601); 长春市社会发展科技计划项目(2012111-12SF39);

摘要

介绍了一种采用双传感器差分算法分析人体肢段双向偏转角并进行肢段定位的新方法;基于本方法开发了一套使用三轴加速度计的可穿戴式传感系统,用于获取和分析下肢肢段前后摆角和左右偏转角信息。为了评估本方法,将该系统分别在二自由度机械臂和受验志愿者大腿上进行了测试。结果表明:在理想条件下,只使用加速度计组成可穿戴式传感系统,通过测量髋关节和大腿上的加速度,就可以得到人体局部坐标系内下肢段定向的动态分析。

关键词: 生物医学工程; 双传感器差分算法; 可穿戴传感器系统; 肢段定位

中图分类号:TP212.9 文献标志码:A 文章编号:1671-5497(2014)04-1016-08

Ambulatory assessment of human segmental orientation using accelerometers

LIU Kun, HAN Xuan, LIU Zheng

College of Mechanical Science and Engineering, Jilin University, Changchun 130022, China

Abstract

A new method using a double-sensor difference based algorithm for analyzing human segment rotational angles in two directions for segmental orientation analysis in three-dimensional (3D) space was presented. A wearable sensor system based only on triaxial accelerometers was developed to obtain the pitch and yaw angles of thigh segment with an accelerometer approximating translational acceleration of the hip joint and two accelerometers measuring the actual accelerations on the thigh. To evaluate the method, the system was tested on a mechanical arm of two degrees of freedom and on the thighs of eight volunteer subjects. The results show that, without integration and switching between different sensors, using only one kind of sensor, the wearable sensor system is suitable for ambulatory analysis of normal gait orientation of thigh and shank in two directions of the segment-fixed local coordinate system in 3D space. It can then be applied to assess spatio-temporal gait parameters and monitoring the gait function of patients in clinical settings.

Keyword: biomedical engineering; double-sensor difference based algorithm; wearable sensor system; segmental orientation

Show Figures

0 引言

在医学领域中,人体运动参数,特别是下肢的运动情况对于临床医生制定诊疗方案具有重要作用^{[ 1, 2]}。在量化外科手术效果和评估患者下肢康复运动状况方面,步态分析已经变成一种有效的诊疗参考手段^{[ 3]}。因此,检测下肢段的运动定位情况很有必要。为了实现应用传感器进行步态分析,国内外已研发了多种可穿戴式传感器系统^{[ 4, 5, 6, 7, 8, 9]}。例如,在下肢段运动位置的测量方面,已经可以采用加速度计和(或)陀螺仪估算出下肢关节角度^{[ 10, 11]}。然而,当采用加速度计测量人体下肢段加速度时,测量信号是一个合成加速度,它由重力加速度、平移加速度、肢段旋转加速度及误差信号组成,这些分加速度并不能在测得的加速度中分辨出来^{[ 12]}。文献[13]中通过对陀螺仪测得的角速度进行数值积分获得肢段转动角位移,但是积分结果会由于信号漂移而产生失真。因此,如果仅仅简单地把实际检测得到的合加速度视为所测位置的角加速度,然后直接积分获得肢段角速度和角位移^{[ 14]},尽管受验者肢体在低速运动时,所测加速度已经很接近角加速度,但是实测到的合加速度除了肢段角加速度外,仍然含有以上提到的其他加速度分量,这些必将导致积分误差,使得所求的肢段摆动角速度和角位移并不准确。另外,如果肢段角位移采用含有竖直方向加速度 a_z的等式 θ=(180 /π×arcsin( a_z/g))来计算,那么,测量时必须使受验者保持静止,或者在非静止状态下测量时,忽略线性加速度分量。可见这种方法只适合测量静态时的下肢段定位,对于运动的人体,采用这种方法进行下肢定位测量和计算并不十分准确。Luinge和Veltink于2005年提出了另一种方法^{[ 15]},但是在测量过程中需要不断地重新校准陀螺仪的偏移量和方向。文献[16]中提出了一种解决这个矛盾的方法,通过加速度计和陀螺仪的测量信号分别计算角位移,然后根据下肢摆动频率来切换所要采用的计算结果。然而这个切换频率定为多少是合适的,又是一个比较难以确定的问题。文献[17]中给出了另一种计算关节角的方法,但是该方法采用了3种传感器(陀螺仪、加速度计和磁力计),并且同样仅适用于人体静态模式下的检测评估,没有考虑人体运动时线性加速度的存在。

本文提出一种适合单片机运算的简单算法,仅采用受验者身上的加速度计所测数据对下肢定位和其他步态参数进行测量计算。提出的双传感器差分算法能够计算局部坐标系内下肢肢段双向旋转状况,从而实现受验者行走时大腿肢段前屈/后伸和外展/内收角度的计算,因为本文方法不需要使用陀螺仪测量数据,所以不会出现前述方法中提到的用陀螺仪测量数据计算角度时的积分误差。

此外,当传感器固定在下肢上的时候,由于冲击载荷和肌肉活动,所测信号极易受皮肤运动的影响。因此,采用加速度计所测数据进行下肢肢段定位的运算评估时,需做如下假设:认为下肢段是刚体,并且受验者沿直线向前行走,躯干摆动很小,测量所受皮肤运动的干扰很小,并且腿部没有明显的内外扭转。基于此条件,当两个加速度计同轴同向地安装在肢段两个不同位置时,除了旋转加速度之外,重力加速度、平移加速度、皮肤运动影响和其他干扰对于两个传感器的作用应该是一样的。为了利用两个旋转加速度之间的差异达到测量下肢肢段在空间运动定位的目的,下面给出一种新型的基于双传感器测量信号差异的差分算法,来评估下肢段在两个方向上的转动情况。为了验证这个方法,在实验部分开发了一套基于三轴加速度计的可穿戴传感系统,并在机械臂和人体肢段上进行了测试和验证。

1 方法介绍

应用加速度计测量信号时,所得信号为合加速度,其中的平移加速度分量、重力加速度分量以及误差信号等并不能单独分离出来^{[ 18]}。当不考虑误差与干扰时,一个三轴加速度计安装在刚体局部坐标系内的已知位置 r上,所测加速度 a如下所示:

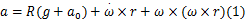
式中: R是刚体对地姿态矩阵; a₀是刚体局部坐标系原点对地加速度; g=(0,0, -g)^T是重力场; ω是刚体在局部坐标系内的角速度。

1.1 平面坐标系内分析转动刚体定位的双传感器差分算法

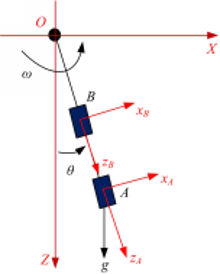
为了分析平面内刚体的旋转,引入3个参考坐标系:在刚体旋转点定义一个固定的全局坐标系 XOZ,另外两个局部坐标系 X_AO_AZ_A和 X_BO_BZ_B分别定义在两个传感器所固定的 A和 B位置, Z_A和 Z_B轴沿刚体长度方向,如图1所示。则 A和 B处的加速度和角位移关系通过下列表达式得出:

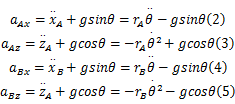
式中:( a_Ax, a_Az)和( a_Bx, a_Bz)是局部坐标系 X_AO_AZ_A和 X_BO_BZ_B内各传感器相应轴向的加速度;( x_A, z_A)和( x_B, z_B)是 A、 B点在全局坐标系内的坐标; θ是刚体在全局坐标系 XOZ中的转角位移。

	Figure Option View Download New Window
	图1 平面坐标系内刚体的运动示意图Fig.1 Motion of a rigid body in 2D coordinate frame

根据式(2)· r_B-式(4)· r_A和式(3)· r_B-式(5)· r_A,得出角位移计算式如下:

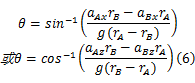
根据式(2)~(4)和式(3)~(5),刚体的角速度和角加速度计算式如下:

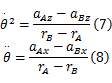
式中:旋转点到 A、 B点的距离 r_A、 r_B可直接用尺测出; a_Ax、 a_Bx、 a_Az、 a_Bz可通过加速度计测出。

1.2 下肢肢段定位角度的计算

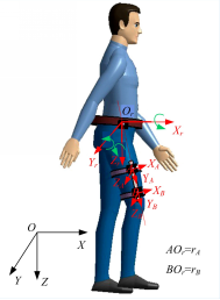
为了确定局部坐标系中人体肢段的定位角度,以分析三维空间中大腿与骨盆的相对姿态为例,测量右侧大腿的旋转角度,并作以下设定:认为髋关节为理想球套关节,允许大腿在3个方向的自由运动(前屈/后伸,外展/内收和大腿的向内/向外旋转)。引入图2中坐标系来表示髋关节的前屈/后伸和外展/内收:

(1) O-XYZ是全局坐标系, X轴向体前, Y轴向体右, Z轴竖直向下。

(2) O_r-X_rY_rZ_r是髋关节处固定的局部坐标系,原点 O_r在髋关节。当人体只向前做无转身的平移运动时,各轴在三维空间中保持与全局坐标系相应各轴平行。在求解髋关节旋转时^{[ 19]}, Y_r轴描述前屈 /后伸运动, X_r轴描述外展/内收运动。

(3) A-x_Ay_Az_A和 B-x_By_Bz_B是两个加速度计传感器的局部坐标系,加速度计分别安装在大腿的 A、 B位置。 z_A轴沿大腿骨径向, x_A轴在股骨矢状面内与 z_A轴垂直。两个坐标系 o_B-x_By_Bz_B与 o_A-x_Ay_Az_A中相对应的轴方向相同(同轴同向)。

受验者进行直线行走实验时,局部坐标系的原点 O_r(髋关节)随身体向前只做矢状面内的平移运动,即本文只考虑髋关节的平移加速度,则大腿上 A点的实际合加速度( a_A)可通过加速度计测量并且通过下式表示:

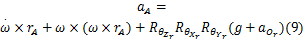
式中: 是全局坐标系内髋关节的平移加速度;( g+ )是髋关节的实测加速度,在下面的等式中将用表示; 是关于 Y_r轴的屈 /伸角(俯仰角); 是关于 X_r轴的外展 /内收角(偏航角); 是关于 Z_r轴的向内/向外转角; 、和是对应的旋转矩阵。

	Figure Option View Download New Window
	图2 加速度计在下肢的安装位置示意图Fig.2 Schematic diagram of lower limb with accelerometers

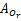
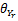
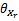
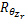
如图2所示,两个相同的三轴加速度计以同轴同向的方式分别固定在大腿上 A、 B位置,因此,能够测量出 A和 B位置的两组加速度 a_A和 a_B,加速度计安装到位后,测量旋转半径( r_A和 r_B),于是得到下面的等式:

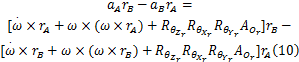
根据等式(6)中计算角位移的方法,局部坐标系中关于 X_r、 Y_r和 Z_r轴的角位移可从式(10)中计算出来。为了简化计算,如前所述,认为受验者是沿直线向前行走,不考虑躯干发生扭动和肌肉运动造成的误差,不考虑腿部向内/向外的偏转。只用角 θ_Yr和 θ_Xr来描述局部坐标系内大腿运动时的角度定位,得到计算式如下:

如等式(11)(12)所示,仅用加速度计所测的3个位置(髋关节和大腿上任意两点)的实际加速度( 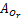, a_A和 a_B)就能获得局部坐标系内大腿相对躯干的前屈/后伸、外展/内收的角度。

1.3 实验设计

在第一个实验中,为了在简化的理想情况下检验该方法,装配了一个由刚性轴和编码器组成的二自由度机械臂,由手驱动模拟下肢摆动。如图3所示,在机械装置的两个旋转轴 X_r和 Y_r处分别安装编码器(RS-32-0/1000ER.11KB),用来测量机械臂关于 X_r和 Y_r轴的转角。为了测量机械臂的加速度,按照前述方法,机械臂的相应位置固定了两个同轴同向的三轴加速度计。

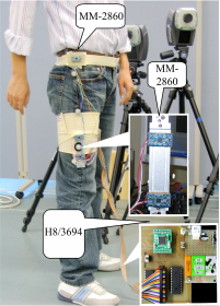
在第二个实验中,基于前述的理论方法,初步制作了一套可穿戴式传感检测系统,分别固定于髋关节处和大腿上。该系统采用了三片三轴加速度计和一片MCU,如图4所示。单片机用来实时存储与处理加速度计测量的信号,并且可在检测完毕后与PC机离线通信,把存储的测量信号传到电脑,以备后期信号处理与分析。

	Figure Option View Download New Window
	图3 参考机械臂系统及可穿戴传感系统Fig.3 Reference mechanical system and wearable sensor system

	Figure Option View Download New Window
	图4 应用所开发设备对大腿进行方向定位检测分析Fig.4 Thigh orientation analysis with developed device

对比理论方法中的理想假设发现,在实验中还是存在一定的实际问题,即很难精确地把加速度计固定于髋关节去测量理想的髋关节处的点加速度。但是,本实验中髋关节和受验者躯干向前平移运动时的加速度是相同的,所以,可以把加速度计固定在髋关节之上的腰胯部位所测的加速度信号作为理论方法中的髋关节加速度。本实验中,第一个加速度计固定于髋关节之上的腰部,可以获得更稳定的加速度。但是应该注意的是:加速度计在腰胯部应尽量保持竖直,才能最大程度地保证所测加速度与理论方法中描述的理想平移加速度一致,也才能保证重力加速度最大程度上在加速度计的 Z轴上测得。因此,安放在腰胯部的这个加速度计首先被固定在了一块平面铝板上,然后再通过松紧带固定在腰胯部。在初始校准时,应将带有加速度计的铝板最大程度地调整到竖直方向,即与大腿的矢径面一致,并且保持加速度计的 Z轴竖直向下。

为采集大腿上两点的加速度,两片加速度计被同轴同向地固定于一片L形不反光的铝板上,并在L形铝板的端点和拐角处固定3个反光球,作为摄像拍摄参考点。在每位受验者使用穿戴式传感系统进行测试的初始安装中,应校准两个加速度计在大腿肢段的方向与髋关节和膝关节的连线保持一致。

本文实验中,8位受验者(6男2女,年龄为(25±3)岁,身高为(170±5) cm,体重为(60±11) kg无肌肉骨骼损伤等病史,要求他们在自选的慢速、正常和快速下沿直线行走测试。每次运动测试中,可通过穿戴传感系统获得三组加速度信号。同时,应用实验室光学运动分析系统(NAC Hi-Dcam II高速数码摄像系统)测量反光球的三维轨迹,分析得出受验者下肢运动参数,作为本传感器检测方法的标准参考值。

2 实验结果

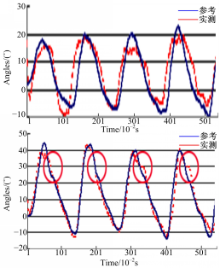
实验所测信号由MCU存储后,离线传到计算机后经Matlab分析处理。图5和图6分别给出了在高角速度(85°/s)和低角速度(55°/s)模式下,从传感系统和编码器中得到的关于 X_r和 Y_r轴的实测角位移和参考角位移。图7和图8中分别给出了在受验者自选慢速和快速行走时,基于实测信号的关于 X_r和 Y_r轴的大腿运动转角曲线。

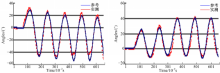	Figure Option View Download New Window
	图5 当机械臂高速摇摆时关于 X_r和 Y_r轴的计算角速度和参考角速度Fig.5 Calculated and referenced angular displacements about X_r and Y_r axes when mechanical arm swung at a higher speed

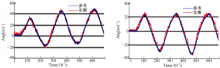	Figure Option View Download New Window
	图6 当机械臂低速摇摆时关于 X_r和 Y_r轴的计算角速度和参考角速度Fig.6 Calculated and referenced angular displacements about the X_r and Y_r axes when mechanical arm swung at a lower speed

	Figure Option View Download New Window
	图7 在自选慢速情况下关于 X_r和 Y_r轴的计算角位移和参考角位移Fig.7 Calculated and referenced angular displacements about X_r and Y_r axes at self-selected slow speed

	Figure Option View Download New Window
	图8 在自选快速情况下关于 X_r和 Y_r轴的计算角位移和参考角位移Fig.8 Calculated and referenced angular displacements about the X_r and Y_r axes at self-selected high speed

3 分析与讨论

在不同实验情况下,关于 X_r轴和 Y_r轴的参考角位移和实测角位移之间的分析数据已列在表1~表4中,其中RMSE为均方根误差, R是相关系数, r_A和 r_B是每个三轴加速度计的旋转半径, e_max是最大误差,ROM是在各方向上被测物体的转动范围。如表1和表2所示,当 r_A和 r_B的值相同但是机械臂的转速不同时,转速越高导致 e_max和RMSE越大,相关系数 R越小。当转速相同但 r_A和 r_B不同时, r_A和 r_B之间的差值越大,导致 e_max和RMSE越小,相关系数 R越大。这表明计算得到的角位移精度与加速度计之间的距离和机械臂的转速有关。因此,为了获得更精确的角位移和转速,可增加两片加速度计之间的距离并且减小机械臂转速。

表1 基于机械臂系统编码器和传感检测系统轴加速度计检测结果的关于 X_r轴角位移的对比 Table 1 Result comparison of angular displacement about X_r axis between referenced mechanical system and two triaxial accelerometers based measuring system

表2 基于机械臂系统编码器和传感检测系统轴加速度计检测结果的关于 Y_r轴角位移的对比 Table 2 Result comparison of angular displacement around Y_raxis between the referenced mechanical system and two triaxial accelerometers based measuring system

当在大腿上应用所开发的可穿戴传感检测系统测试时,从髋关节到大腿上第一个加速度计的距离 r_A取决于在每次测试时它被固定的位置,范围是(200±50) mm。

如表3和表4所示,在大腿上检测并计算得到的角位移的 e_max和RMSE比在机械臂上检测计算所得到的数值大得多,这是因为相对于机械臂而言,很难把可穿戴传感系统稳定地固定在大腿上。尤其是在快速步行时,由于肌肉运动引起的冲击载荷会导致传感器在肢体表面的不稳定,为所测加速度增加了干扰误差。此外,髋关节处的加速度计也不能像理论设计中那样被精确地固定在髋关节中。随着步行速度的增加,局部坐标原点的非平移加速度也会增大,这将导致更大的误差,尤其是当腰胯部的加速度计不是完全竖直时,重力加速度将会在各轴上都产生分量,这也会导致计算误差。因此,为了得到髋关节更精确的平移加速度,应该改进加速度计在腰胯部的固定方法。此外,从对比结果看,第一个实验中的机械臂是二自由度的刚性臂,驱动它摆动时完全没有 Z轴方向的转动,这也使得由等式(11)和(12)在不考虑 Z轴转动下求解二自由度旋转肢段定位更加精确。当计算大腿的方向角时,忽略了躯干摆动,尽管受验者已经尽量保持正向前行,但因个人行走时而实际存在的躯干摆动也必然会存在并引起误差。

表3 在不同步态速度条件(平均值±SD)下,摄像机参考系统和可穿戴传感检测系统关于 X_r轴角位移的对比 Table 3 Result comparison of angular displacements around X_r axis(yaw angle)between referenced camera system and developed wearable sensor system under gait velocity conditions(mean±SD)

表4 在不同步态速度条件(平均值±SD)下,摄像机参考系统和可穿戴传感检测系统关于 Y_r轴角位移的对比 Table 4 Result comparison of angular displacements around Y_r axis(pitch angle)between referenced camera system and developed wearable sensor system under gait velocity conditions(mean±SD)

当受验者执行3种不同速度的行走实验时,在每次步态的摆动阶段后期,大腿开始主动减速,并且大腿的倾斜和偏移角位移逐渐达到最大值^{[ 20]}。当身体继续向前移动时,髋关节也随之向前移动。在脚触地之前,大腿的角位移逐渐减小。当脚触地时,身体重量转移到该侧肢体上,于是脚与地面的反作用力立即增加,随后在径向方向上的加速度急剧上升。因此,由传感器得到的实测结果与由摄像系统得到的参考数据之间的最大误差发生在整个步态的这一阶段,如图7和图8中圆圈内部分所示。

4 结束语

本文给出的创新型双传感器差分算法是积分算法的一种改进,本文实验虽是在理想假设情况下进行的,但是从量化的实验结果来看,充分验证了本文方法的可行性与正确性,并得出定性的结论:本文方法可以应用于开发可穿戴传感器系统。但值得提出的是,如果想进一步把该方法应用于开发满足临床应用精度的可穿戴式传感系统,还需要进一步改善测量方法,提高测量精度。实验结果表明,重力场下的三维空间中,在肢段局部坐标系内,基于双传感器差分算法在两个轴向上对身体肢段定位进行动态测量分析是可行的。这也表明,仅使用加速计一种传感器,应用无积分误差的简单算法就可实现对人体肢段定位评估。本文方法和所开发的实际设备,可以运用于步态分析,再进一步加以改进,可为研究人员或者临床医生提供准确的肢体运动分析信息。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Findlow A, Goulermas J Y, Nester C, et al. Predicting lower limb joint kinematics using wearable motion sensors[J]. Gait & Posture, 2008, 28(1): 120-126. [本文引用:1] [JCR: 1.969]
[2]	Favre J, Jolles B M, Aissaoui R, et al. Ambulatory measurement of 3D knee joint angle[J]. Journal of Biomechanics, 2008, 41(5): 1029-1035. [本文引用:1] [JCR: 2.716]
[3]	Aminian K, Trevisan C, Najafi B, et al. Evaluation of an ambulatory system for gait analysis in hip osteoarthritis and after total hip replacement[J]. Gait & Posture, 2004, 20(1): 102-107. [本文引用:1] [JCR: 1.969]
[4]	Mayagoitiaa Ruth E, Neneb Anand V, Veltinkc Peter H. Accelerometer and rate gyroscope measurement of kinematics: an inexpensive alternative to optical motion analysis systems[J]. Journal of Biomechanics, 2002, 35(4): 537-542. [本文引用:1] [JCR: 2.716]
[5]	Turcot K, Aissaoui R, Boivin K, et al. New accelerometric method to discriminate between asymptomatic subjects and patients with medial knee osteoarthritis during 3-D gait[J]. IEEE Transactions on Biomedical Engineering, 2008, 55(4): 1415-1422. [本文引用:1] [JCR: 2.348]
[6]	Kavanagh J J, Menz H B. Accelerometry: a technique for quantify movement patterns during walking[J]. Gait & Posture, 2008, 28(1): 1-15. [本文引用:1] [JCR: 1.969]
[7]	Nyan M N, Tay F E H, Seah K H W, et al. Classification of gait patterns in the time-frequency domain[J]. Journal of Biomechanics, 2006, 39(14): 2647-2656. [本文引用:1] [JCR: 2.716]
[8]	Liu Kun, Liu Tao, Shibata K, et al. Novel approach for lower limb segment orientation in gait analysis using triaxial accelerometers[C]∥IEEE/ASME International Conference on Advanced Intelligent Mechatronics, 2008: 488-492. [本文引用:1]
[9]	Williamson R, Andrews B J. Detecting absolute human knee angle and angular velocity using accelerometers and rate gyroscopes[J]. Medical And Biological Engineering and Computing, 2001, 39(3): 294-302. [本文引用:1] [JCR: 1.79]
[10]	Mehmet Engin, Alparslan Demirel, Engin Zeki, et al. Recent developments and trends in biomedical sensors[J]. Measurement, 2005, 37: 173-188. [本文引用:1] [JCR: 1.13]
[11]	Roetenberg D, Slycke P J, Veltink P H. Ambulatory position and orientation tracking fusing magnetic and inertial sensing[J]. IEEE Transactions on Biomedical Engineering, 2007, 54(3): 883-890. [本文引用:1] [JCR: 2.348]
[12]	Kavanagh J J, Morrison S, James D A, et al. Reliability of segmental accelerations measured using a new wireless gait analysis system[J]. Journal of Biomechanics, 2006, 39(15): 2863-2872. [本文引用:1] [JCR: 2.716]
[13]	Jolles Dejnabadi H, Casanova Brigitte M, Pascal Emilio Fua, et al. Estimation and visualization of sagittal kinematics of lower limbs orientation using body-fixed sensors[J]. IEEE Transactions on Biomedical Engineering, 2006, 53(7): 1385-1392. [本文引用:1] [JCR: 2.348]
[14]	Zijlstra Agnes, Goosen Jon H M, Verheyen Cees C P M, et al. A body-fixed-sensor based analysis of compensatory trunk movements during unconstrained walking[J]. Gait & Posture, 2008, 27(1): 164-167. [本文引用:1] [JCR: 1.969]
[15]	Luinge H J, Veltink P H. Measuring orientation of human body segments using miniature gyroscopes and accelerometers[J]. Medical and Biological Engineering and Computing, 2005, 43(2): 273-282. [本文引用:1] [JCR: 1.79]
[16]	Dejnabadi H, Jolles B M, Aminian K. A new approach to accurate measurement of uniaxial joint angles based on a combination of accelerometers and gyroscopes[J]. IEEE Transactions on Biomedical Engineering, 2005, 52(8): 1478-1484. [本文引用:1] [JCR: 2.348]
[17]	O'Donovan Karol J, Kamnik Roman, O'Keeffe Derek T, et al. An inertial and magnetic sensor based technique for joint angle measurement[J]. Journal of Biomechanics, 2007, 40(12): 2604-2611. [本文引用:1] [JCR: 2.716]
[18]	Hagemeister Nicola, Parent Gerald, Van de Putte Maxime. A reproducible method for studying three-dimensional knee kinematics[J]. Journal of Biomechanics, 2005, 38(9): 1926-1931. [本文引用:1] [JCR: 2.716]
[19]	Zatsiorsky V M. Kinematics of Human Motion[M]. Champaign, LI: Human Kinetics, 2002. [本文引用:1]
[20]	Rose Jessica, Gamble James G. Human Walking, 3rd ed[M]. New York: Lippincott Williams & Wilkins, 2006: 111-114. [本文引用:1]

2008

1.969

0.0

. 2008, 28(1):120-126 DOI:10.1016/j.gaitpost.2007.11.001

Predicting lower limb joint kinematics using wearable motion sensors

Abstract The aim of this study was to estimate sagittal plane ankle, knee and hip gait kinematics using 3D angular velocity and linear acceleration data from motion sensors on the foot and shank. We explored the accuracy of intra-subject predictions (i.e., where training and testing uses trials from the same subject) and inter-subject (where testing uses subjects different from the ones used for training) predictions, and the effect of loss of sensor data on prediction accuracy. Hip, knee and ankle kinematic data were collected using reflective markers. Simultaneously, foot and shank angular velocity and linear acceleration data were collected using small integrated accelerometers/gyroscope units. A generalised regression networks algorithm was used to predict the former from the latter. The best results were from intra-subject predictions, with very high correlations (0.93–0.99) and low mean absolute deviation (≦2.3°) between measured kinematic joint angles and predicted angles. The inter-subject case produced poorer correlations (0.70–0.89) and larger absolute differences between measured and predicted angles, ranging from 4.91° (left ankle) to 9.06° (right hip). The angular velocity data added little to the accuracy of predictions and there was also minimal benefit to using sensor data from the shank. Thus, a wearable system based only on footwear mounted sensors and a simpler sensor set providing only acceleration data shows potential. Whilst predictions were generally stable when sensor data was lost, it remains to be seen whether the generalised regression networks algorithm is robust for other activities such as stair climbing.

... 0 引言在医学领域中,人体运动参数,特别是下肢的运动情况对于临床医生制定诊疗方案具有重要作用^[1,2] ...

2008

2.716

0.0

. 2008, 41(5):1029-1035 DOI:10.1016/j.jbiomech.2007.12.003

Ambulatory measurement of 3D knee joint angle

Abstract Three-dimensional measurement of joint motion is a promising tool for clinical evaluation and therapeutic treatment comparisons. Although many devices exist for joints kinematics assessment, there is a need for a system that could be used in routine practice. Such a system should be accurate, ambulatory, and easy to use. The combination of gyroscopes and accelerometers (i.e., inertial measurement unit) has proven to be suitable for unrestrained measurement of orientation during a short period of time (i.e., few minutes). However, due to their inability to detect horizontal reference, inertial-based systems generally fail to measure differential orientation, a prerequisite for computing the three-dimentional knee joint angle recommended by the Internal Society of Biomechanics (ISB). A simple method based on a leg movement is proposed here to align two inertial measurement units fixed on the thigh and shank segments. Based on the combination of the former alignment and a fusion algorithm, the three-dimensional knee joint angle is measured and compared with a magnetic motion capture system during walking. The proposed system is suitable to measure the absolute knee flexion/extension and abduction/adduction angles with mean (SD) offset errors of −1° (1°) and 0° (0.6°) and mean (SD) root mean square (RMS) errors of 1.5° (0.4°) and 1.7° (0.5°). The system is also suitable for the relative measurement of knee internal/external rotation (mean (SD) offset error of 3.4° (2.7°)) with a mean (SD) RMS error of 1.6° (0.5°). The method described in this paper can be easily adapted in order to measure other joint angular displacements such as elbow or ankle.

... 0 引言在医学领域中,人体运动参数,特别是下肢的运动情况对于临床医生制定诊疗方案具有重要作用^[1,2] ...

2004

1.969

0.0

. 2004, 20(1):102-107 DOI:10.1016/S0966-6362(03)00093-6

Evaluation of an ambulatory system for gait analysis in hip osteoarthritis and after total hip replacement

Abstract Spatial and temporal parameters of gait have clinical relevance in the assessment of motor pathologies, particularly in orthopaedics. A new gait analysis system is proposed which consists of (a) an ambulatory device (Physilog ® ) including a set of miniature gyroscopes and a portable datalogger, and (b) an algorithm for gait analysis. The aim of this study was the validation of this system, for accuracy and clinical applicability. Eleven patients with coxarthrosis, eight patients with total hip arthroplasty and nine control subjects were studied using this portable system and also a reference motion analyzer and force plate. The small differences in the stance period (19±31 ms), stride length and velocity (0.4±9.6 cm and 2.5±8.3 cm/s, respectively), as well as thigh and shank rotations (2.4±4.3° and 0.3±3.3°, respectively), confirmed good agreement of the proposed system with the reference system. In addition, nearly the same accuracy was obtained for all three groups. Gait analysis based on Physilog ® was also in agreement with their Harris Hip Scores (HHS): the subjects with lower scores had a greater limp, a slower walking speed and a shorter stride. This ambulatory gait analysis system provides an easy, reproducible and objective method of quantifying changes in gait after joint replacement surgery for coxarthrosis.

... 在量化外科手术效果和评估患者下肢康复运动状况方面,步态分析已经变成一种有效的诊疗参考手段^[3] ...

2002

2.716

0.0

. 2002, 35(4):537-542 DOI:10.1016/S0021-9290(01)00231-7

Accelerometer and rate gyroscope measurement of kinematics: an inexpensive alternative to optical motion analysis systems

Abstract A general-purpose system to obtain the kinematics of gait in the sagittal plane based on body-mounted sensors was developed. It consisted of four uniaxial seismic accelerometers and one rate gyroscope per body segment. Tests were done with 10 young healthy volunteers, walking at five different speeds on a treadmill. In order to study the system's accuracy, measurements were made with an optic, passive-marker system and the body-mounted system, simultaneously. In all the comparison cases, the curves obtained from the two systems were very close, showing root mean square errors representing

... 为了实现应用传感器进行步态分析,国内外已研发了多种可穿戴式传感器系统^{[4,5,6,7,8,9]} ...

2008

2.348

0.0

... 为了实现应用传感器进行步态分析,国内外已研发了多种可穿戴式传感器系统^{[4,5,6,7,8,9]} ...

2008

1.969

0.0

. 2008, 28(1):1-15 DOI:10.1016/j.gaitpost.2007.10.010

Accelerometry: a technique for quantify movement patterns during walking

Abstract The popularity of using accelerometer-based systems to quantify human movement patterns has increased in recent years for clinicians and researchers alike. The benefits of using accelerometers compared to more traditional gait analysis instruments include low cost; testing is not restricted to a laboratory environment; accelerometers are small, therefore walking is relatively unrestricted; and direct measurement of 3D accelerations eliminate errors associated with differentiating displacement and velocity data. However, accelerometry is not without its disadvantages, an issue which is scarcely reported in gait analysis literature. This paper reviews the use of accelerometer technology to investigate gait-related movement patterns, and addresses issues of acceleration measurement important for experimental design. An overview of accelerometer mechanics is provided before illustrating specific experimental conditions necessary to ensure the accuracy of gait-related acceleration measurement. A literature review is presented on how accelerometry has been used to examine basic temporospatial gait parameters, shock attenuation, and segmental accelerations of the body during walking. The output of accelerometers attached to the upper body has provided useful insights into the motor control of normal walking, age-related differences in dynamic postural control, and gait patterns in people with movement disorders.

... 为了实现应用传感器进行步态分析,国内外已研发了多种可穿戴式传感器系统^{[4,5,6,7,8,9]} ...

2006

2.716

0.0

... 为了实现应用传感器进行步态分析,国内外已研发了多种可穿戴式传感器系统^{[4,5,6,7,8,9]} ...

2008

0.0

... 为了实现应用传感器进行步态分析,国内外已研发了多种可穿戴式传感器系统^{[4,5,6,7,8,9]} ...

2001

1.79

0.0

. 2001, 39(3):294-302 DOI:10.1007/BF02345283

Detecting absolute human knee angle and angular velocity using accelerometers and rate gyroscopes

1.LLC Second Sight Stanford California USA Stanford California USA 2.National Spinal Injuries Center at the Stoke Mandeville Hospital UK UK 3.University of Reading Department of Cybernetics UK UK

Knee joint angle and angular velocity were calculated in real time during standing up and sitting down. Two small modules comprising rate gyroscopes and accelerometers were attached to the thigh and shank of two able-bodied volunteers and one T 5 ASIA(A) paraplegic assisted by functional electrical stimulation (FES). The offset and drift of the rate gyroscopes was compensated for by auto-resetting and auto-nulling algorithms. The tilt of the limb segments was calculated by combining the signals of the accelerometer and the rate gyroscope. The joint angle was calculated as the difference in tilt of the segments. The modules were also tested on a two-dimensional model. The mean differences between the rate gyroscope-accelerometer system and the reference goniometer for the model, able-bodied and paraplegic standing trials were 2.1°, 2.4° and 2.3° respectively for knee angle and 2.3° s −1 , 5.0° s −1 and 11.8° s −1 respectively for knee velocity. The rate gyroscope-accelerometer system was more accurate than using the accelerometer as a tilt meter, possibly due to the greater bandwidth of the rate gyroscope-accelerometer system.

... 为了实现应用传感器进行步态分析,国内外已研发了多种可穿戴式传感器系统^{[4,5,6,7,8,9]} ...

2005

1.13

0.0

. 2005, 37:null-null

Recent developments and trends in biomedical sensors

... 例如,在下肢段运动位置的测量方面,已经可以采用加速度计和(或)陀螺仪估算出下肢关节角度^[10,11] ...

2007

2.348

0.0

... 例如,在下肢段运动位置的测量方面,已经可以采用加速度计和(或)陀螺仪估算出下肢关节角度^[10,11] ...

2006

2.716

0.0

... 然而,当采用加速度计测量人体下肢段加速度时,测量信号是一个合成加速度,它由重力加速度、平移加速度、肢段旋转加速度及误差信号组成,这些分加速度并不能在测得的加速度中分辨出来^[12] ...

2006

2.348

0.0

2008

1.969

0.0

. 2008, 27(1):164-167 DOI:10.1016/j.gaitpost.2007.02.010

A body-fixed-sensor based analysis of compensatory trunk movements during unconstrained walking

Abstract This paper presents a body-fixed-sensor (BFS) based approach for quantifying compensatory trunk movements during unconstrained walking. Orientation of trunk segments was calculated by fusing low-pass filtered accelerometer data and high-pass filtered data from gyroscopes. To evaluate accuracy, frontal plane angular movements of the pelvis during different treadmill walking conditions were compared to results based on a high-accuracy camera system. Mean differences between the two methods remained within 0.31°, standard deviations of differences within 1.4° and error percentages within 17.7%. Correlations ranged from 0.87 to 0.99. To test whether the method could discriminate between hip arthroplasty patients with and without compensatory trunk movements, the BFS based method was applied to patients and healthy controls during overground walking. Within a walking speed range of 0.40–1.10 m/s, the peak-to-peak amplitudes of trunk movements ranged from 5.7° to 7.9° in healthy subjects and from 13.5° to 26.3° versus 7.4° to 13.8° in patients with and without compensatory trunk movements, respectively. The presented BFS based approach can be used to assess spatio-temporal gait parameters and trunk movements and thus to objectively monitor gait function in hip arthroplasty patients in a clinical setting.

... 因此,如果仅仅简单地把实际检测得到的合加速度视为所测位置的角加速度,然后直接积分获得肢段角速度和角位移^[14],尽管受验者肢体在低速运动时,所测加速度已经很接近角加速度,但是实测到的合加速度除了肢段角加速度外,仍然含有以上提到的其他加速度分量,这些必将导致积分误差,使得所求的肢段摆动角速度和角位移并不准确 ...

2005

1.79

0.0

. 2005, 43(2):273-282 DOI:10.1007/BF02345966

Measuring orientation of human body segments using miniature gyroscopes and accelerometers

1.University of Twente Signals Systems Group, Department of Electrical Engineering Enschede The Netherlands Enschede The Netherlands

In the medical field, there is a need for small ambulatory sensor systems for measuring the kinematics of body segments. Current methods for ambulatory measurement of body orientation have limited accuracy when the body moves. The aim of the paper was to develop and validate a method for accurate measurement of the orientation of human body segments using an inertial measurement unit (IMU). An IMU containing three single-axis accelerometers and three single-axis micromachined gyroscopes was assembled in a rectangular box, sized 20×20×30 mm. The presented orientation estimation algorithm continuously corrected orientation estimates obtained by mathematical integration of the 3D angular velocity measured using the gyroscopes. The correction was performed using an inclination estimate continuously obtained using the signal of the 3D accelerometer. This reduces the integration drift that originates from errors in the angular velocity signal. In addition, the gyroscope offset was continuously recalibrated. The method was realised using a Kalman filter that took into account the spectra of the signals involved as well as a fluctuating gyroscope offset. The method was tested for movements of the pelvis, trunk and forearm. Although the problem of integration drift around the global vertical continuously increased in the order of 0.5° s −1 , the inclination estimate was accurate within 3° RMS. It was shown that the gyroscope offset could be estimated continuously during a trial. Using an initial offset error of 1 rad s −1 , after 2 min the offset error was roughly 5% of the original offset error. Using the Kalman filter described, an accurate and robust system for ambulatory motion recording can be realised.

... Luinge和Veltink于2005年提出了另一种方法^[15],但是在测量过程中需要不断地重新校准陀螺仪的偏移量和方向 ...

2005

2.348

0.0

2007

2.716

0.0

. 2007, 40(12):2604-2611 DOI:10.1016/j.jbiomech.2006.12.010

An inertial and magnetic sensor based technique for joint angle measurement

Abstract This paper describes the design and evaluation of a miniature kinematic sensor based three dimensional (3D) joint angle measurement technique. The technique uses a combination of rate gyroscope, accelerometer and magnetometer sensor signals. The technique enables 3D inter-segment joint angle measurement and could be of benefit in a variety of applications which require monitoring of joint angles. The technique is not dependent on a fixed reference coordinate system and thus may be suitable for use in a dynamic system such as a moving vehicle. The technique was evaluated by applying it to joint angle measurement of the ankle joint. Experimental results show that accurate measurement of ankle joint angles is achieved by the technique during a variety of lower leg exercises including walking.

2005

2.716

0.0

... 1 方法介绍应用加速度计测量信号时,所得信号为合加速度,其中的平移加速度分量、重力加速度分量以及误差信号等并不能单独分离出来^[18] ...

2002

0.0

. 2002, :-

Kinematics of Human Motion

根据眼球的三维静力学模型与眼球运动的三维动力学模型建立的非线性方程组所求得的结果,利用Visual C++编程语言初步建立了眼球的三维立体模型,并设计了眼球运动的动画程序.介绍了程序各个组成模块的主要属性和主要功能,给出了程序设计过程所用到的坐标系统设定方式、控制界面的主要功能和动画实现的主要过程.

... 在求解髋关节旋转时^[19],Y_r轴描述前屈/后伸运动,X_r轴描述外展/内收运动 ...

2006

0.0

... 当受验者执行3种不同速度的行走实验时,在每次步态的摆动阶段后期,大腿开始主动减速,并且大腿的倾斜和偏移角位移逐渐达到最大值^[20] ...