基于自纠正最小和的LDPC译码改进算法

doi:10.13229/j.cnki.jdxbgxb.20221526

摘要/Abstract

摘要：

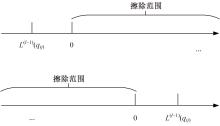
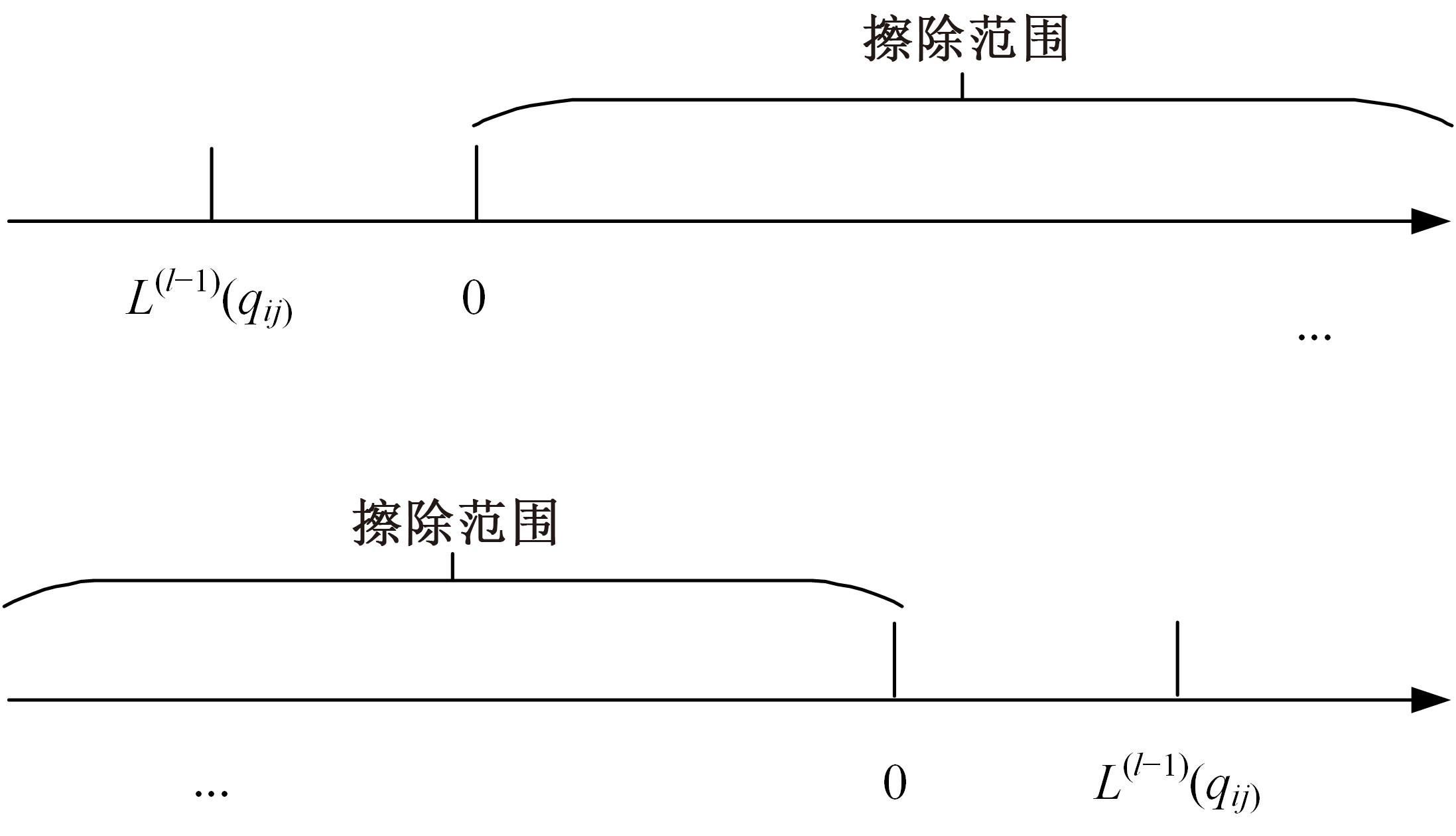
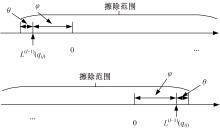
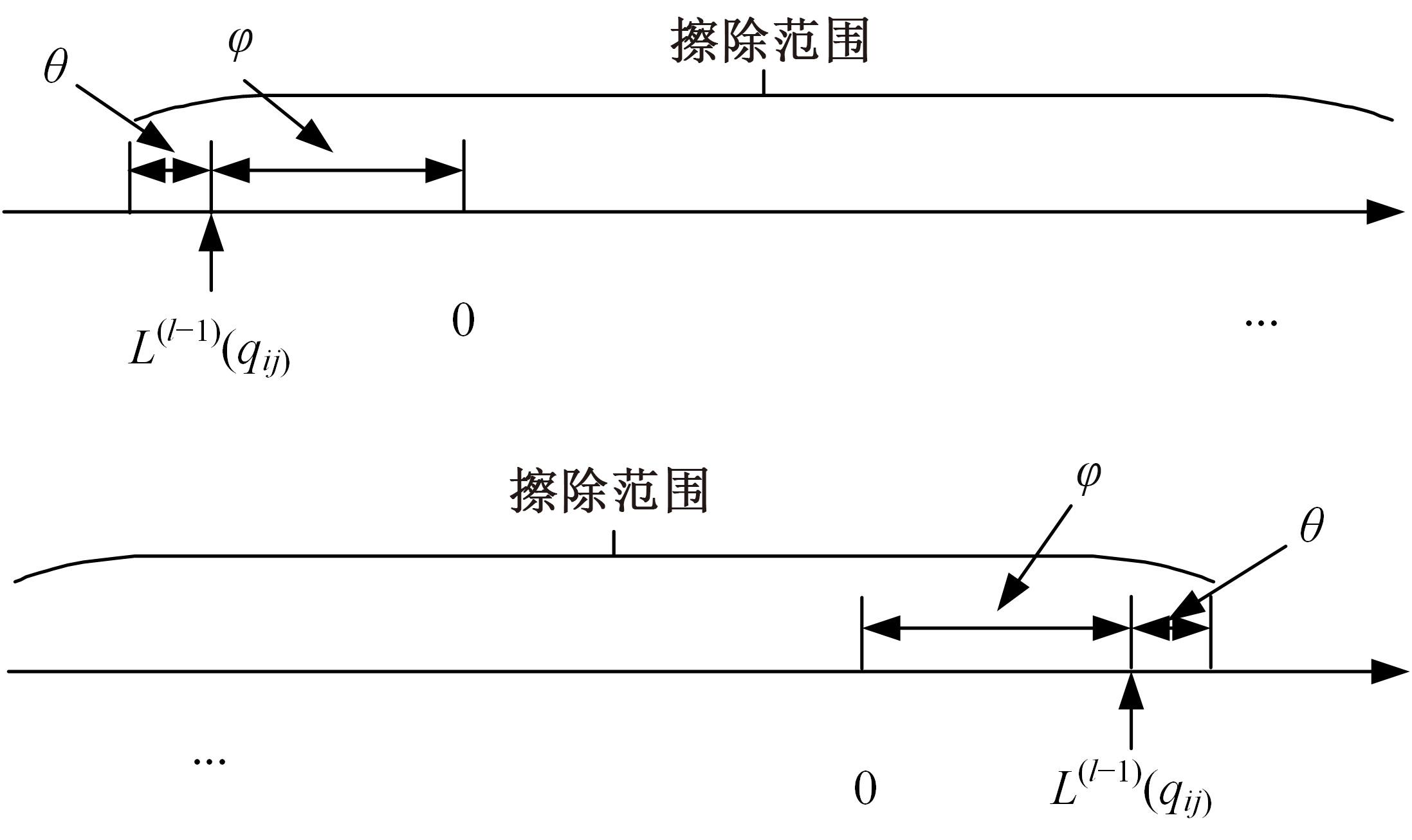
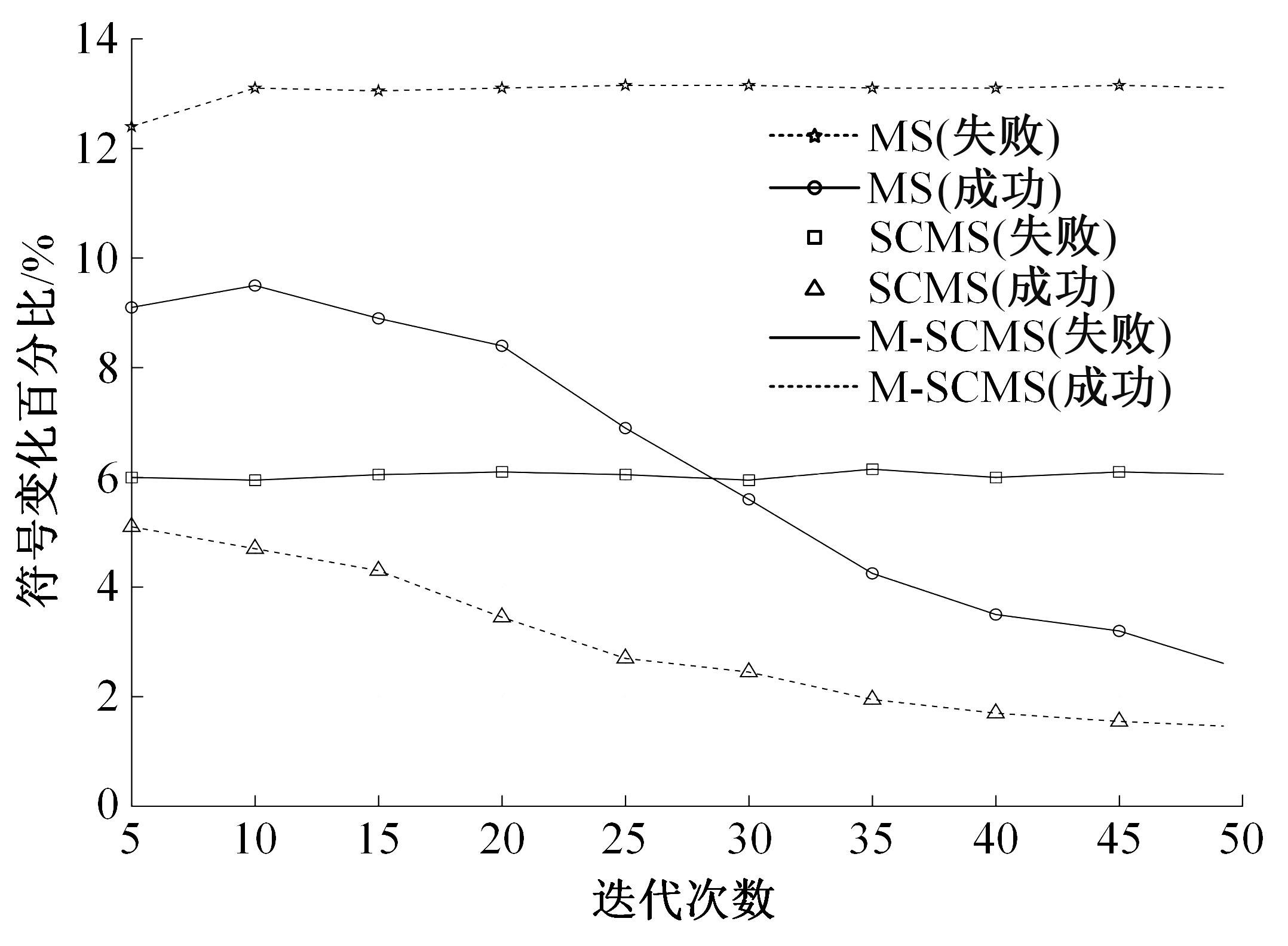
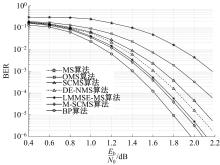
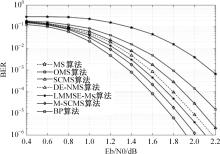
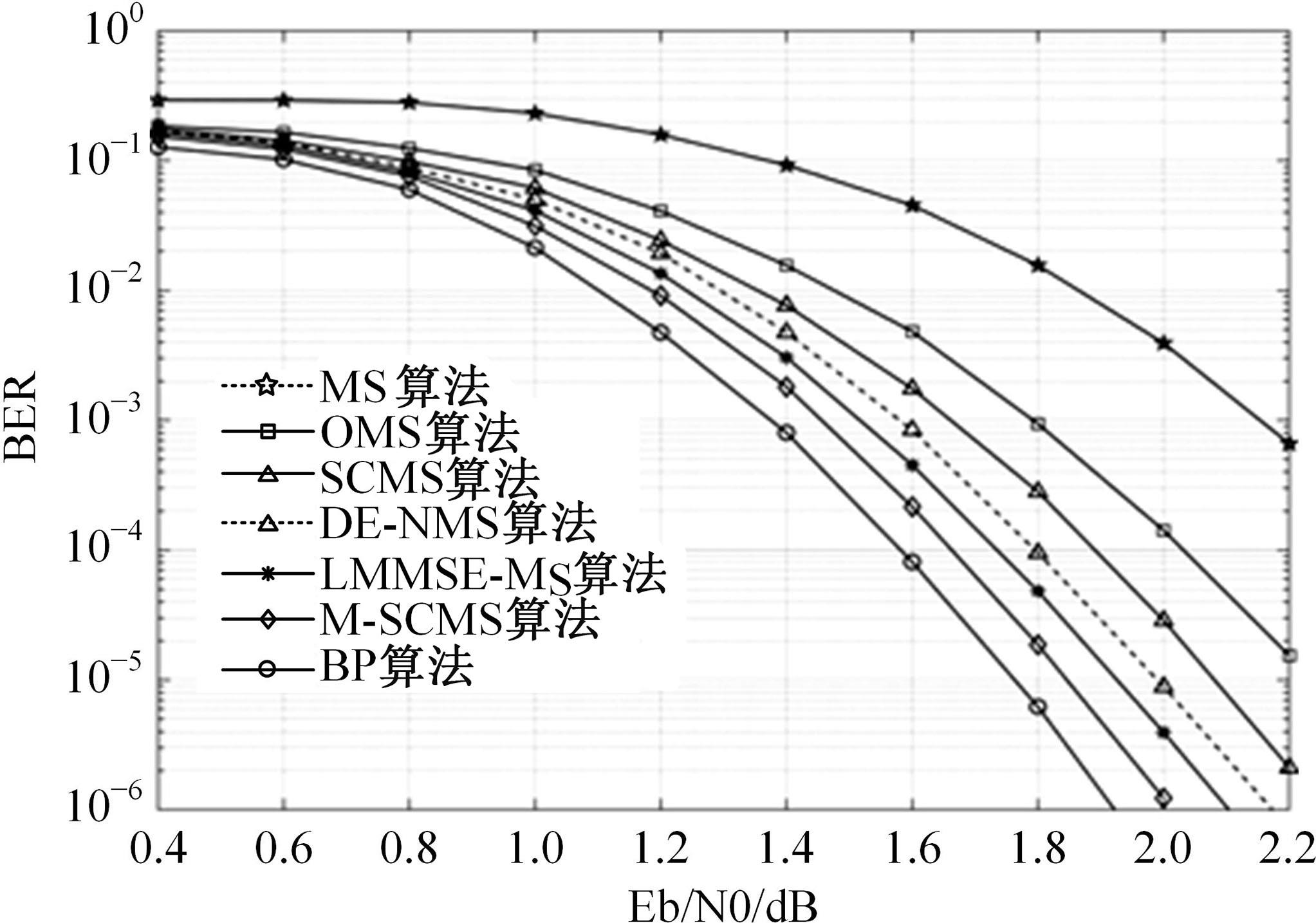
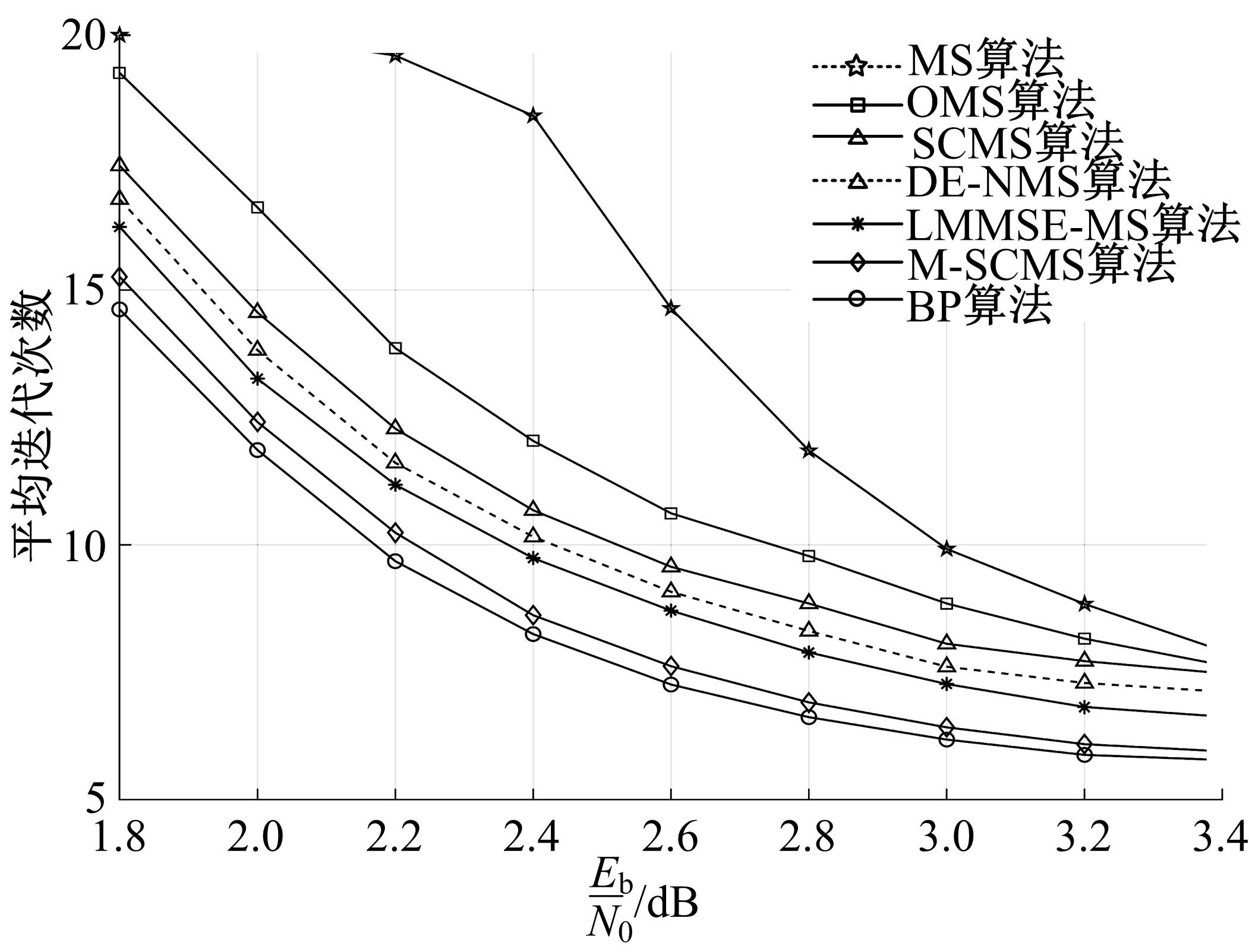
针对低密度奇偶校验码（LDPC）中非零元素含量较低，导致在译码过程中存在节点信息可靠度判定不够准确的问题，本文提出了一种基于自纠正最小和的LDPC译码改进算法。分析置信传播（BP）译码算法的迭代规律，利用最小和算法的第一最小值和第二最小值设置变量节点信息的修正阈值，改进自纠正最小和算法。采用次序统计量理论获取与两个最小值对应的归一化因子，阻止不可靠变量节点信息在迭代译码过程中的传递扩散。仿真结果表明：在误比特率为10^-5时，该算法可获得约0.2 dB的译码性能增益，平均迭代次数最多可降低18.2%，证明所提算法可有效提高译码性能和迭代收敛性能。

关键词: LDPC码, 自纠正最小和算法, 修正阈值, 次序统计量, 置信传播算法

Abstract:

Low density parity check code is a kind of linear block code. Due to the low content of non-zero elements， there is a problem that the node information reliability determination is not accurate enough in the decoding process. Therefore， an improved LDPC decoding algorithm based on self correcting minimum sum is proposed. The iteration rule of BP decoding algorithm is analyzed. The first minimum and the second minimum of the minimum sum algorithm are used to set the correction threshold of variable node information， and the self-corrected min-sum algorithm is improved. The order statistics theory is used to obtain the normalization factor corresponding to the two minimum values to prevent the transmission and diffusion of unreliable variable node information in the iterative decoding process. Simulation results show that when the bit error rate is 10^-5， the proposed algorithm can obtain about 0.2 dB of decoding performance gain， and the average number of iterations can be reduced by 18.2% at most， which proves that the proposed algorithm can effectively improve the decoding performance and iterative convergence performance.

Key words: LDPC code, self-corrected min-sum algorithm, modified threshold, order statistic, belief propagation algorithm

中图分类号:

TN911.22

江虹,徐洪亮. 基于自纠正最小和的LDPC译码改进算法[J]. 吉林大学学报(工学版), 2024, 54(4): 1136-1143.

Hong JIANG,Hong-liang XU. Improved algorithm based on self-corrected min-sum decoding for LDPC codes[J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(4): 1136-1143.

图/表 7

图1

图2

图3

图4

图5

表 1

图6

参考文献 20

1	Indoonundon M, Pawan F T. Overview of the challenges and solutions for 5G channel coding schemes[J]. Journal of Information and Telecommunication, 2021, 5(4): 460-483.
2	HU D W. On the implementation of 5G LDPC decoder[J]. Journal of Electronics & Information Technology,2021, 43(4): 1112-1119.
3	Wu X, Tian J Q, Yang X Y. Fast encoding algorithm for 5G new radio LDPC code[J]. Communications Technology, 2022, 55(1): 30-35.
4	Myung S, Park S I, Kim K J, et al. Offset and normalized min-sum algorithms for ATSC 3.0 LDPC decoder[J]. IEEE Trans on Broadcasting, 2017, 63(4): 734-739.
5	TRAN-THI B N, NGUYEN-LY T, Hong H N, et al. An improved offset min-sum LDPC decoding algorithm for 5G new radio[C]∥International Symposium on Electrical and Electronics Engineering (ISEE), Piscataway, USA, 2021: 106-109.
6	Shrinidhi J, Krishna P S, Yamuna B, et al. Modified min sum decoding algorithm for low density parity check codes[J]. Procedia Computer Science, 2020, 171: 2128-2136.
7	Wang X, Cao W, Li J, et al. Improved min-sum algorithm based on density evolution for low-density parity check codes[J]. IET Communications, 2017, 11(10): 1582-1586.
8	Chen F T, Zhang Y S, Du Z. Low complexity offset min-sum algorithm for 5G low density parity check codes[J]. Journal of Computer Applications, 2020, 40(7): 2028-2032
9	Nam-Ii K I M, Seung-Que L E, Jin-Up K I M. A modified min sum decoding algorithm based on approximation enhancement for LDPC codes[C]∥International Conference on Information and Communication Technology Convergence, Jeju, Korea (South), 2020: 1407-1410.
10	Wang D T, Zhou H, Qian H Y. LDPC Adaptive minimum sum decoding algorithm and its FPGA implementation[J]. Computer Science, 2021, 48(Sup.1): 608-612.
11	Zavertkin K, Panarina A, Ovinnikov A, et al. Efficient BP-based decoding algorithms for QC-LDPC codes[C]∥The 10th Mediterranean Conference on Embedded Computing, Budva, Montenegro,2021: 1-4.
12	Nimara S. Reliability assessment of flooded min-sum LDPC decoders based on sub-threshold processing units[C]∥The 22nd Euromicro Conference on Digital System Design, Kallithea, Greece, 2019: 620-623.
13	Sun R, Hou X, Sun J, et al. Reliability-based-layered belief propagation for iterative decoding of LDPC codes[C]∥IEEE International Symposium on Information Theory, Vail, USA, 2018: 1156-1160.
14	LIU X, YANG D, WANG Z. Improved decoding algorithms of LDPC codes based on reliability metrics of variable nodes[J]. IEEE Access, 2019, 7: 35769-35778.
15	Yacoub E B. Matched quantized min-sum decoding of low-density parity-check codes[C]∥IEEE Information Theory Workshop, Riva del Garda, Italy, 2021: 1-5.
16	Chen R, Chen L. Dual threshold self-corrected minimum sum algorithm for 5G LDPC decoders[J]. Information, 2020, 11(7): 355.
17	Li X, Zhang L, Tan J, et al. An improved self-corrected min-sum decoding for LDPC codes[C]∥The 16th International Conference on Intelligent Systems and Knowledge Engineering, Chengdu, China, 2021: 152-156.
18	Chen R, Chen L. A dynamic self-corrected minimum sum decoding algorithm for LDPC codes[J]. Journal of Beijing University of Posts and Telecommunications, 2020, 43(4): 15-20.
19	Chen F T, Li H B, Li P A. Improved algorithm based on offset min-sum decoding for LDPC codes[J]. Systems Engineering and Electronics, 2022, 44(7): 2350-2356.
20	Wu H, Wang H. A high throughput implementation of QC-LDPC codes for 5G NR[J]. IEEE Access, 2019, 7: 185373-185384.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

算法	Multiplication	Division	Addiction
BP	11NW-6（N+K）	N（W+1）	N（3W+1）
MS	0	0	N（4W-1）+K（lbW-2）
OMS	0	0	N（4W-1）+K（lbW-2）
SCMS	0	0	N（4W-1）+K（lbW-2）
DE-NMS	NW	0	N（4W-1）+K（lbW-2）
LMMSE-MS	NW	0	N（4W-1）+K（lbW-2）
M-SCMS	2NW	0	N（5W-1）+K（lbW-2）

[1]	李思佳, 毛玉泉, 曹祥玉, 裴鑫, 尹忠海. QC-LDPC码的普适Kronecker积-逐步边增加算法[J]. 吉林大学学报(工学版), 2013, 43(01): 244-249.
[2]	韩维, 黄建国, 韩晶. LDPC码在水下语音通信中的性能[J]. 吉林大学学报(工学版), 2010, 40(05): 1377-1380.
[3]	杨建华,,赵旦峰,赵春晖. LDPC编码超宽带系统的迭代多用户检测算法[J]. 吉林大学学报(工学版), 2009, 39(06): 1654-1658.
[4]	赵旦峰, 刘腾宇, 杨大伟, 石雷. 改进的 LDPC 码译码算法[J]. 吉林大学学报(工学版), 2009, 39(04): 1090-1093.
[5]	赵旦峰，佟宁宁，吴宇平 . 具有线性编码复杂度的非规则LDPC码[J]. 吉林大学学报(工学版), 2009, 39(02): 504-0507.
[6]	杨建华;赵旦峰;赵春晖 . 一种内部自适应的LDPC编码超宽带系统 [J]. 吉林大学学报(工学版), 2008, 38(03): 715-0718.