基于自适应莱维多样性的改进蚁群算法

doi:10.13229/j.cnki.jdxbgxb.20230372

摘要/Abstract

摘要：

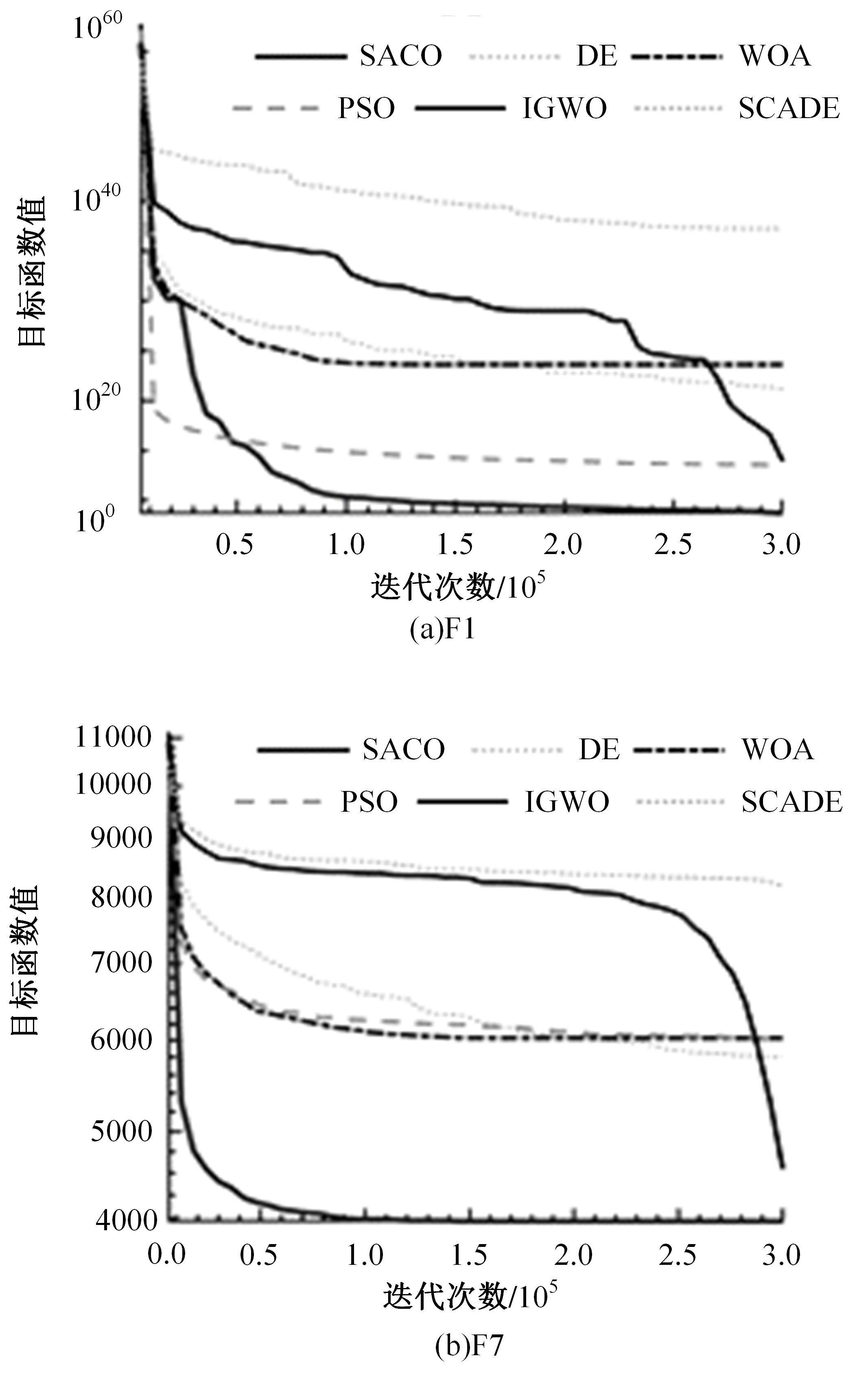
本文提出了一种基于自适应莱维（Lévy）多样性机制的改进蚁群优化（SACO）算法解决算法存在收敛精度差、易陷入局部最优的问题，并将新算法应用到焊接梁工程优化问题中。SACO算法结合该机制随机步长搜索的特点提升种群多样性，使算法避免局部最优。进一步，本文设计了一系列实验测试SACO算法的性能。实验结果显示，该算法在函数实验中表现出更好的收敛性、更高的精度及更强的避免陷入局部最优的能力。最后在工程应用实验结果中，SACO算法在函数优化和焊接梁优化上展现出较强的竞争力，可作为现实工程问题求解的有效工具。

关键词: 群智能算法, 蚁群算法, 工程优化, 莱维多样性机制

Abstract:

The papers proposed an improved ant colony optimization algorithm（SACO） based on the adaptive Lévy diversity mechanism to enhance convergence accuracy and the ability to avoid local optimum. The new algorithm was applied to welded beam engineering optimization problem. SACO combines the mechanism to enhance the population diversity， making the algorithm avoid local optimum. The paper designed a series of experiments to test the performance of SACO. Experimental results show that the algorithm shows better convergence， accuracy， and the ability to avoid local optimization in function experiments. Meanwhile， the proposed algorithm is applied to the welded beam design problem， obtaining significantly better results than other comparison algorithms. SACO shows competitiveness in function optimization and welded beam design optimization， which can be used as an effective tool for solving real-life engineering problems.

Key words: swarm intelligence algorithm, ant colony optimization, engineering optimization, Lévy diversity mechanism

中图分类号:

TP305

杨娇寰,王鹏. 基于自适应莱维多样性的改进蚁群算法[J]. 吉林大学学报(工学版), 2024, 54(10): 2978-2983.

Jiao-huan YANG,Peng WANG. Improved ant colony algorithm based on adaptive Lévy diversity[J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(10): 2978-2983.

图/表 4

表1

表2

图1

表3

参考文献 23

1	Socha K, Dorigo M. Ant colony optimization for continuous domains[J]. European Journal of Operational Research, 2008, 185(3): 1155-1173.
2	Zhao D, Liu L, Yu F H,et al. Ant colony optimization with horizontal and vertical crossover search: fundamental visions for multi-threshold image segmentation[J]. Expert Systems with Applications, 2021, 167(114122): 1-38.
3	赵鑫, 杨雄飞, 钱育蓉. 改进的蚁群优化算法求解旅行商问题[J]. 计算机工程与设计,2022, 43(4): 962-968.
	Zhao Xin, Yang Xiong-fei, Qian Yu-rong. Improved ant colony optimization algorithm for TSP[J].Computer Engineering and Design, 2022, 43(4): 962-968.
4	肖耀涛. 基于改进蚁群优化算法的云计算资源调度[J]. 微型电脑应用, 2022, 38(2): 160-163.
	Xiao Yao-tao.Cloud computing resource scheduling based on improved ant colony optimization algorithm[J].Microcomputer Applications, 2022, 38(2): 160-163.
5	朱显辉, 于越, 师楠, 等.BP神经网络的分层优化研究及其在风电功率预测中的应用[J].高压电器,2022, 58(2): 158-170.
	Zhu Xian-hui, Yu Yue, Shi Nan, et al. Research on hierarchical optimization of bp neural network and its application in wind power prediction[J].High Voltage Apparatus, 2022, 58(2): 158-170.
6	Islam M A, Qi H, RenY T, et al. An inverse simulation for simultaneous identification of randomly oriented arbitrarily shaped particle size distribution and its degree of non-sphericity from spectral transmittance measurement[J]. Measurement Science and Technology, 2021, 32(7): No.075205.
7	Wang Z H, Zhang W J, Liu B, et al. A joint and dynamic routing approach to connected vehicles via LEO constellation satellite networks[J]. Wireless Networks, 2021(2021): No.02712.
8	赵东, 臧雪柏, 赵宏伟. 基于果蝇优化的随机森林预测方法[J]. 吉林大学学报: 工学版, 2017, 47(2): 609-614.
	Zhao Dong, Zang Xue-bai, Zhao Hong-wei. Random forest prediction method based on optimization of fruit fly[J].Journal of Jilin University (Engineering and Technology Edition), 2017, 47(2): 609-614.
9	Xiao J, Li C Q, Zhou J. Minimization of energy consumption for routing in high-density wireless sensor networks based on adaptive elite ant colony optimization[J]. Journal of Sensors, 2021, 2021(2): No.5590951.
10	Xiong N, Zhou X Z, Yang X Q,et al. Mobile robot path planning based on time taboo ant colony optimization in dynamic environment[J]. Frontiers in Neurorobotics, 2021, 15: No.642733.
11	Zhao D, Liu L, Yu F H, et al. Chaotic random spare ant colony optimization for multi-threshold image segmentation of 2D Kapur entropy[J]. Knowledge-Based Systems, 2021, 216(15): No.106510.
12	Brociek R, Wajda A, Slota D. Inverse problem for a two-dimensional anomalous diffusion equation with a fractional derivative of the riemann-liouville type[J]. Energies, 2021, 14(11): 1-17.
13	赵东, 孙明玉, 朱金龙, 等. 结合粒子群和单纯形的改进飞蛾优化算法 [J]. 吉林大学学报: 工学版,2018, 48(6): 1867-1872.
	Zhao Dong, Sun Ming-yu, Zhu Jin-long, et al. Improved moth-flame optimization method based on combination of particle swarm optimization and simplex method[J].Journal of Jilin University (Engineering and Technology Edition), 2018, 48(6): 1867-1872.
14	García S, Fernández A, Luengo J,et al. Advanced nonparametric tests for multiple comparisons in the design of experiments in computational intelligence and data mining: experimental analysis of power[J]. Information Sciences, 2010, 180(10): 2044-2064.
15	Derrac J, García S, Molina D, et al. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms[J]. Swarm and Evolutionary Computation, 2011, 1(1): 3-18.
16	Storn R, Price K. Differential evolution-a simple and efficient heuristic for global[J]. Optimization over Continuous Spaces, 1997, 11(4): 341-359.
17	Mirjalili S, Lewis A.The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51-67.
18	Kennedy J, Eberhart R. Particle swarm optimization[C]//Proceedings of ICNN'95-International Conference on Neural Networks, Perth, Australia, 1995: No.488968.
19	Cai Z N, Gu J H, Luo J, et al. Evolving an optimal kernel extreme learning machine by using an enhanced grey wolf optimization strategy[J]. Expert Systems with Applications, 2019,138: No.112814.
20	Nenavath H, Jatoth R K. Hybridizing sine cosine algorithm with differential evolution for globaloptimization and object tracking[J]. Applied Soft Computing, 2018, 62: 1019-1043.
21	兰淼淼, 胡黄水, 王婷婷, 等. 基于改进鲸鱼优化PID的无刷直流电机转速控制算法[J]. 吉林大学学报: 理学版, 2024, 62(3): 704-712.
	Lan Miao-miao, Hu Huang-shui, Wang Ting-ting, et al. Speed control algorithm of brushless DC motor based on improved whale optimization PID[J]. Journal of Jilin University(Science Edition), 2024, 62(3): 704-712.
22	李汝嘉, 贺壹婷, 季荣彪, 等. 基于量子行为花朵授粉算法优化LSTM模型[J]. 吉林大学学报: 理学版, 2024, 62(5): 1163-1178.
	Li Ru-jia, He Yi-ting, Ji Rong-biao, et al. Optimizing LSTM model based on quantum-inspired flower pollination algorithm[J]. Journal of Jilin University (Science Edition), 2024, 62(5): 1163-1178.
23	胡黄水, 范新纪, 邓育欢. 基于改进Harris鹰优化的无线传感器网络分簇协议[J]. 吉林大学学报: 理学版, 2024, 62(5): 1228-1234.
	Hu Huang-shui, Fan Xin-ji, Deng Yu-huan. Improved Harris hawk optimization based clustering protocol for wireless sensor networks[J]. Journal of Jilin University(Science Edition), 2024, 62(5): 1228-1234.

相关文章 13

[1]	管仁初,贺宝润,梁艳春,时小虎. 基于亲缘关系选择的粒子群优化算法[J]. 吉林大学学报(工学版), 2022, 52(8): 1842-1849.
[2]	朱航,于瀚博,梁佳辉,李宏泽. 基于电场模型的无人机搜寻改进算法及仿真分析[J]. 吉林大学学报(工学版), 2022, 52(12): 3029-3038.
[3]	车翔玖, 张孙旻. 基于异步更新策略的蚁群边缘提取算法[J]. 吉林大学学报(工学版), 2017, 47(5): 1577-1582.
[4]	滕志军, 张帆, 宋明辉. 无线传感器网络能量均衡蚁群路由算法[J]. 吉林大学学报(工学版), 2016, 46(1): 327-332.
[5]	杨庆芳, 梅朵, 韩振波, 张彪. 基于云计算的蚁群算法求解城市路网最短路径[J]. 吉林大学学报(工学版), 2013, 43(05): 1210-1214.
[6]	翟治芬, 严昌荣, 张建华, 张燕卿, 刘爽. 基于蚁群算法和支持向量机的节水灌溉技术优选[J]. 吉林大学学报(工学版), 2013, 43(04): 997-1003.
[7]	申铉京, 刘阳阳, 黄永平, 徐铁, 何习文. 求解TSP问题的快速蚁群算法[J]. 吉林大学学报(工学版), 2013, 43(01): 147-151.
[8]	焦斌, 熊友平, 顾幸生. 改进的蚁群优化算法在无线传感器网络中的应用[J]. 吉林大学学报(工学版), 2011, 41(增刊1): 215-219.
[9]	杨靖^1,2,熊伟丽¹,秦宁宁¹,赵伟³,徐保国¹. 用于无线传感器网络的高能效数据收集算法[J]. 吉林大学学报(工学版), 2011, 41(6): 1720-1725.
[10]	于滨, 刘鸿婷, 闫博, 杨忠振, 赖禄元. 公交线路网优化的双层模型及其解法[J]. 吉林大学学报(工学版), 2010, 40(02): 402-0405.
[11]	陈谋，肖健，姜长生 . 基于改进蚁群算法的无人机三维航路规划[J]. 吉林大学学报(工学版), 2008, 38(04): 991-995.
[12]	李静，刘学，赵健 . 基于蚁群寻优的汽车牵引力PID控制参数整定[J]. 吉林大学学报(工学版), 2008, 38(04): 769-772.
[13]	段海滨, 王道波, 于秀芬 . 基于云模型的小生境MAX-MIN相遇蚁群算法[J]. 吉林大学学报(工学版), 2006, 36(05): 803-0808.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

算法	+/-/=	均值	排名
SACO	~	1.617	1
DE	9/0/1	2.843	3
WOA	10/0/0	4.877	5
PSO	8/1/1	3.563	4
IGWO	7/1/2	2.430	2
SCADE	10/0/0	5.670	6

算法	F1		F2
算法	AVG	STD	AVG	STD
SACO	5.2444E+08	1.5989E+09	8.291 3E+03	1.227 9E+04
DE	1.560 0E+21	5.881 4E+21	2.036 6E+04	5.919 5E+03
WOA	4.155 5E+23	2.260 9E+24	1.640 8E+05	5.519 0E+04
PSO	3.327 3E+13	3.868 3E+13	6.502 2E+02	5.125 6E+01
IGWO	7.843 2E+13	2.882 5E+14	1.258 0E+03	5.171 7E+02
SCADE	1.817 8E+37	7.773 0E+37	6.044 3E+04	6.326 4E+03
算法	F3		F4
算法	AVG	STD	AVG	STD
SACO	4.734 6E+02	2.592 7E+01	5.8626E+02	1.633 6E+01
DE	4.905 8E+02	9.447 3E+00	6.070 9E+02	7.021 7E+00
WOA	5.448 3E+02	3.986 1E+01	7.909 9E+02	6.029 6E+01
PSO	4.783 5E+02	2.428 8E+01	7.473 6E+02	3.374 0E+01
IGWO	5.030 8E+02	2.804 4E+01	6.115 8E+02	2.446 6E+01
SCADE	3.275 8E+03	9.181 5E+02	8.314 3E+02	1.893 9E+01
算法	F5		F6
算法	AVG	STD	AVG	STD
SACO	8.1792E+02	2.543 2E+01	8.9043E+02	2.482 6E+01
DE	8.464 2E+02	8.661 8E+00	9.079 9E+02	9.104 2E+00
WOA	1.194 7E+03	9.676 6E+01	1.002 1E+03	4.361 3E+01
PSO	9.208 8E+02	1.443 3E+01	9.938 1E+02	3.526 9E+01
IGWO	9.120 4E+02	4.126 1E+01	8.938 7E+02	2.336 5E+01
SCADE	1.171 6E+03	3.120 4E+01	1.085 6E+03	1.561 9E+01
算法	F7		F8
算法	AVG	STD	AVG	STD
SACO	4.176 1E+03	6.099 1E+02	2.397 8E+03	2.886 4E+01
DE	5.798 2E+03	2.406 9E+02	2.412 0E+03	6.8674E+00
WOA	6.028 1E+03	7.392 3E+02	2.575 2E+03	5.649 9E+01
PSO	5.996 0E+03	6.155 2E+02	2.536 8E+03	3.633 2E+01
IGWO	4.634 8E+03	6.653 8E+02	2.399 7E+03	2.563 0E+01
SCADE	8.181 0E+03	2.381 9E+02	2.583 9E+03	2.202 9E+01
算法	F9		F10
算法	AVG	STD	AVG	STD
SACO	2.919 8E+03	2.151 7E+01	3.190 2E+03	7.217 6E+01
DE	2.956 4E+03	1.331 6E+01	3.197 5E+03	5.191 0E+01
WOA	3.153 0E+03	9.208 7E+01	3.346 2E+03	2.515 3E+02
PSO	3.189 2E+03	1.027 4E+02	3.246 4E+03	2.243 9E+01
IGWO	2.942 0E+03	3.177 1E+01	3.251 3E+03	3.140 8E+01
SCADE	3.175 7E+03	2.519 6E+01	4.312 2E+03	2.152 4E+02

算法	变量的最有值				最优成本
算法	h	l	t	b	最优成本
SACO	0.182 00	3.731 00	9.042 39	0.205 70	1.7232 02
RO	0.203 69	3.528 47	9.004 23	0.207 24	1.7353 44
SSA	0.205 70	3.471 40	9.036 60	0.205 70	1.724 910
SSA	0.205 70	3.471 40	9.036 60	0.205 70	1.724 910