吉林大学学报(工学版) ›› 2019, Vol. 49 ›› Issue (3): 749-756.doi: 10.13229/j.cnki.jdxbgxb20180120

• • 上一篇    下一篇

基于变间距动态规划的中高速磁悬浮列车 速度曲线优化

赖晴鹰1(),刘军1(),赵若愚1,骆泳吉2,孟令云1,徐亚之3   

  1. 1. 北京交通大学 交通运输学院，北京 100044
    2. 西南交通大学 交通运输与物流学院，成都 610031
    3. 中车唐山机车车辆有限公司，河北 唐山 064000
  • 收稿日期:2018-02-02 出版日期:2019-05-01 发布日期:2019-07-12
  • 通讯作者: 刘军 E-mail:15114243@bjtu.edu.cn;jliu@bjtu.edu.cn
  • 作者简介:赖晴鹰（1991?），男，博士研究生. 研究方向：交通运输规划与管理. E?mail:15114243@bjtu.edu.cn
  • 基金资助:
    国家重点研发计划项目(2016YFB1200601)

Optimal trajectory planning for middle⁃to⁃high speed maglev based on dynamic programming with mutative spacing

Qing⁃ying LAI1(),Jun LIU1(),Ruo⁃yu ZHAO1,Yong⁃ji LUO2,Ling⁃yun MENG1,Ya⁃zhi XU3   

  1. 1. School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044, China
    2. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 610031, China
    3. CRRC Tangshan Co. , Ltd. , Tangshan 064000, China
  • Received:2018-02-02 Online:2019-05-01 Published:2019-07-12
  • Contact: Jun LIU E-mail:15114243@bjtu.edu.cn;jliu@bjtu.edu.cn

RICH HTML

 3   

PDF (PC)

97

摘要：

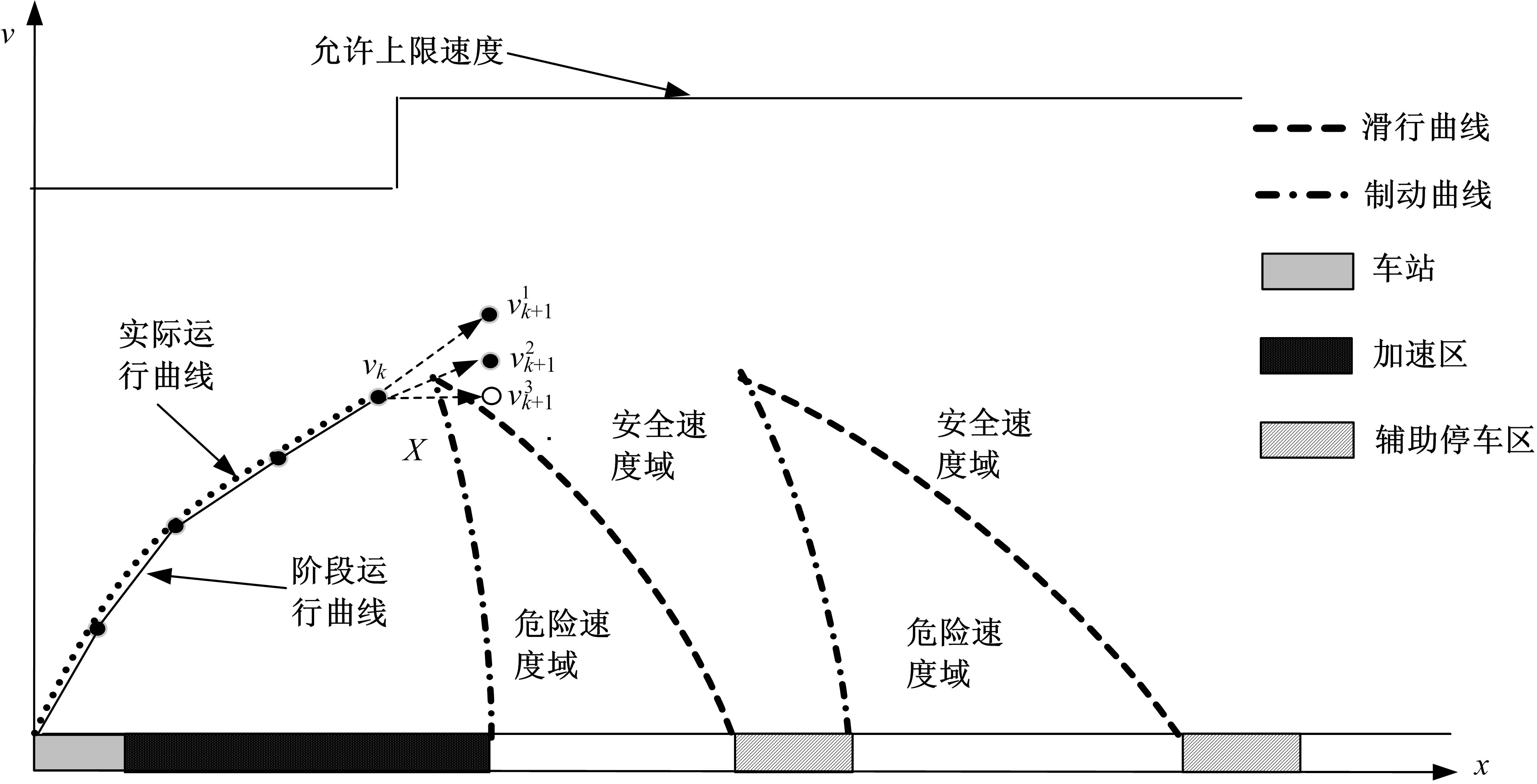
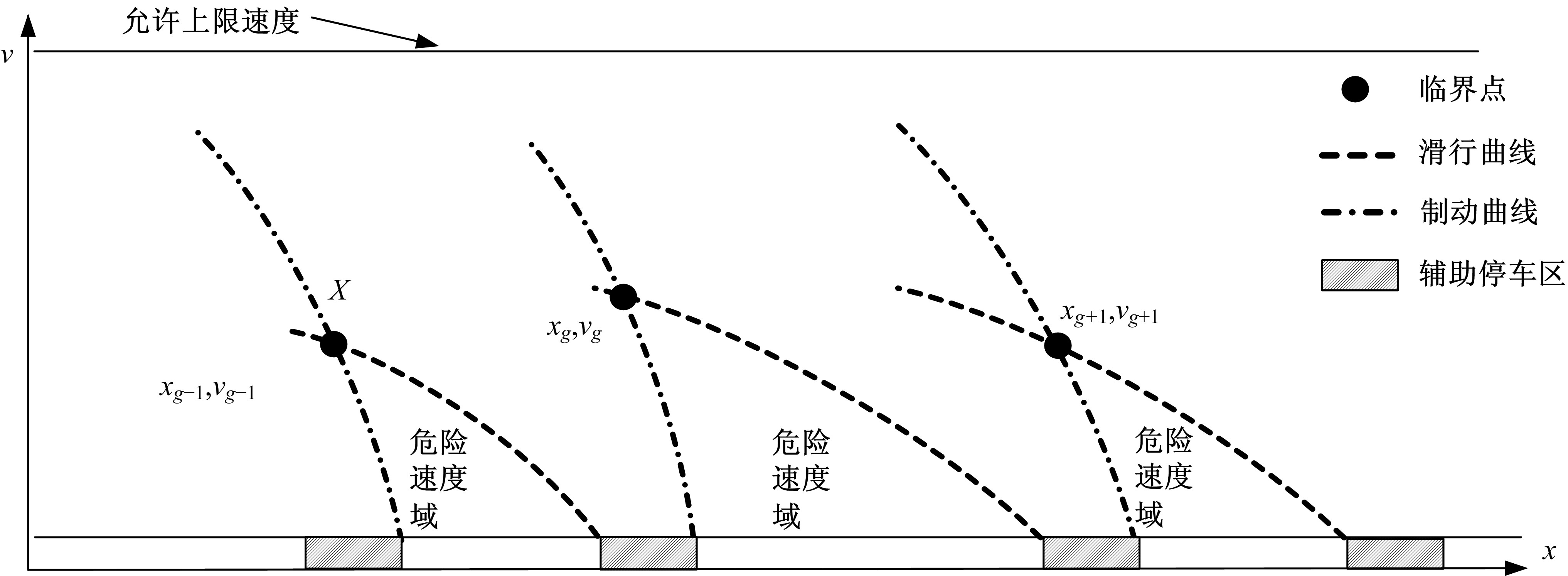
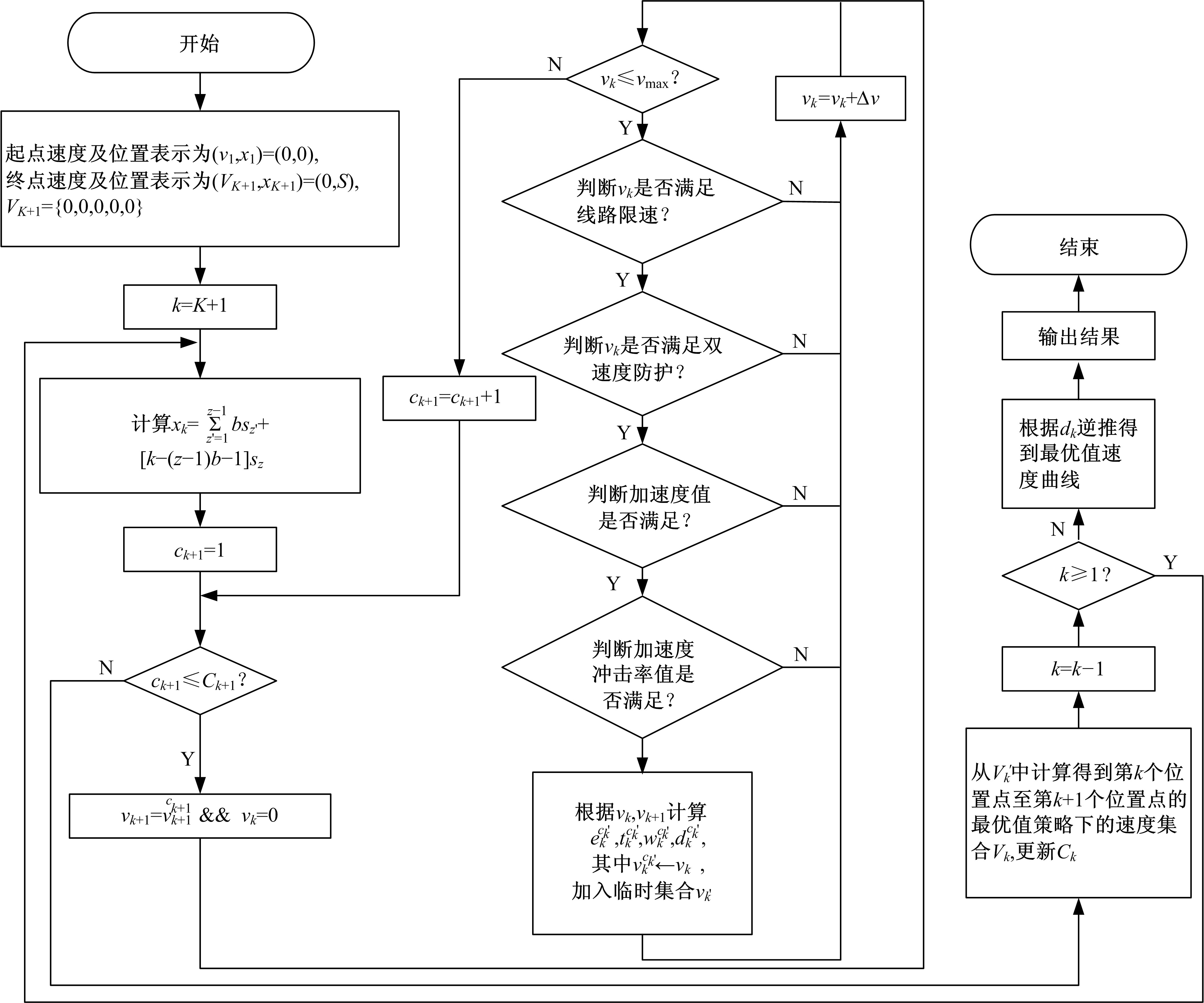
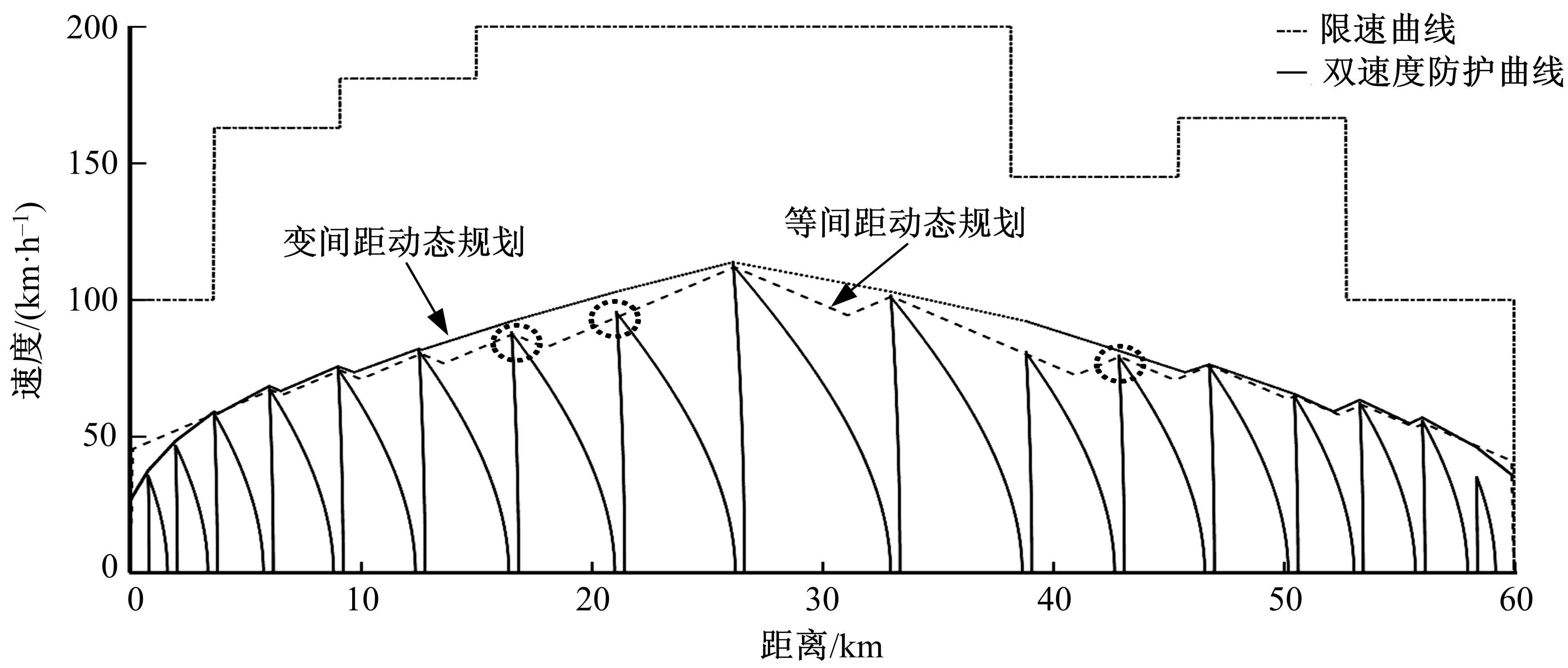
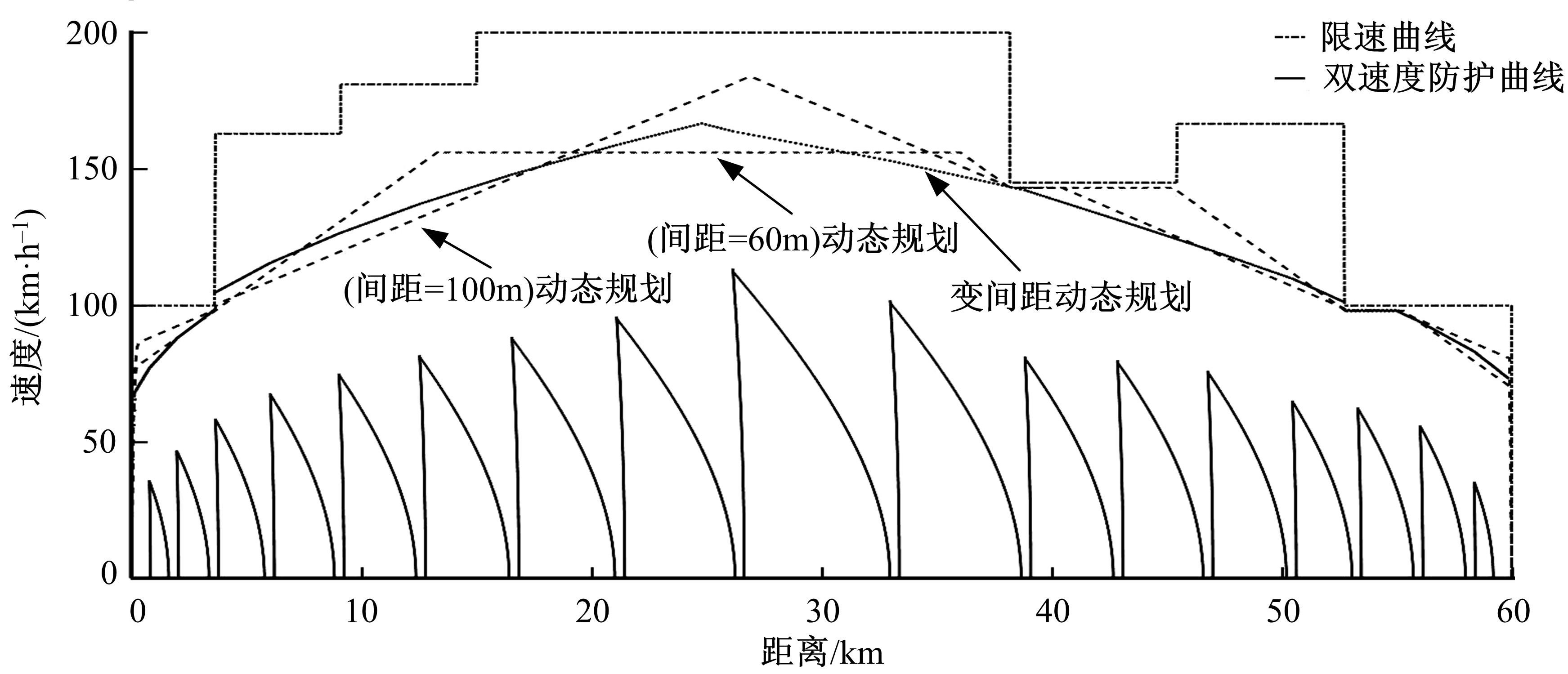
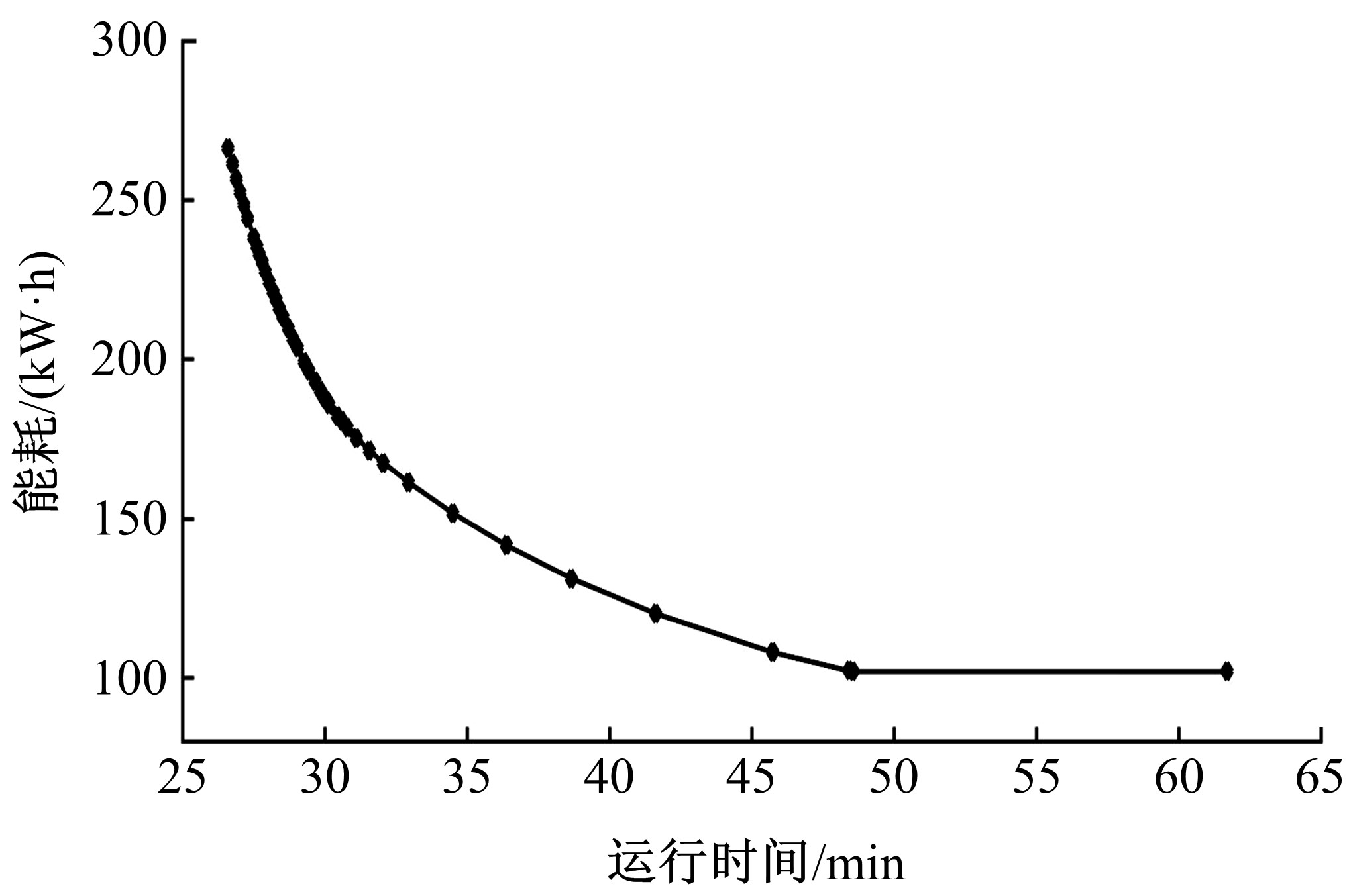
本文首先对中高速磁悬浮列车动力学模型进行分析，之后在考虑辅助停车区对列车运行影响的基础上提出了一种变间距的动态规划模型。该模型以双速度防护曲线临界点作为划分分区的依据，之后将分区再次划分为不同间距长度的子阶段，并构建阶段内能耗以及时间变化方程，最后在满足相关约束条件下采用逆推法求解变间距的动态规划模型。本文通过仿真案例，对比了变间距动态规划模型与等间距动态规划模型在列车速度曲线优化的异同，验证了本文提出的模型在时间效率以及能耗优化上的优势。

关键词: 铁路运输, 中高速磁悬浮, 速度曲线优化, 变间距动态规划, 辅助停车区

Abstract:

A significant approach to save energy of the middle?to?high speed maglev is to optimize the trajectory planning. This paper establishes a model based on dynamic programming with mutative spacing after analyzing the kinetic equations of the middle?to?high speed maglev and the effect of the assistant?stop area. The model firstly uses the crossover point of double protected curve as the foundation of partition. Then, model further divides the partition into small sub?stages with different spacing and formulates the equation of energy and time respectively. Finally, the model is solved by reversing push method under certain constraints. The established model is compared the conventional dynamic programming method through the numerical examples. The results indicate the advantage of the proposed model in energy saving and computational efficiency.

Key words: railway transportation, middle?to?high speed maglev, optimal trajectory planning, dynamic programming with mutative spacing, assistant?stop area

中图分类号: 

  • U293.1

图1

磁悬浮列车纵向受力分析图"

图2

速度转移情况示意图"

图3

双速度曲线防护临界点示意图"

图4

变间距动态规划算法流程图"

表1

辅助停车区位置坐标"

编号起始点/km终止点/km编号起始点/km终止点/km
10.000.821032.9733.38
21.612.041138.6839.10
33.373.771242.6843.11
45.776.201346.5947.01
58.819.231450.2150.63
612.3712.781553.0653.46
716.4116.841655.7256.14
821.0121.441757.9958.41
926.2326.631859.2060.43

表2

区段限速表"

区段/km限速/（km?h–1）
0.0~3.6100
3.6~9.1163
9.1~15.0181
15.0~38.2200
38.2~45.5145
45.5~52.7167
52.7~60.0100

图5

不同模型优化后速度曲线对比分析（运行时间=50 min）"

图6

不同模型优化后速度曲线对比分析（运行时间为30 min）"

表3

不同模型参数对比分析（期望运行时间为30 min）"

情况方法间距/m阶段数能耗/(kW·h)时间误差/%计算时长/s
一变间距动态规划-551196.40.67101.3
二等间距动态规划601000186.70.42565.6
三等间距动态规划100600245.20.33125.6

图7

能耗与运行时间关系图"

1 荀径, 杨欣, 宁滨,等. 列车节能操纵优化求解方法综述[J]. 铁道学报, 2014, 36(4): 14⁃20.
XunJing, YangXin, NingBin, et al. Survey on trajectory optimization for train operation[J]. Journal of the China Railway Society, 2014, 36(4): 14⁃20.
2 杨光. 高速磁悬浮列车最优速度曲线及其跟踪控制研究[D]. 北京: 北京交通大学电子信息工程学院, 2007.
YangGuang. Study on high speed maglev train optimum speed curve and its tracking control[D]. Beijing: College of Electronic Information Engineering, Beijing Jiaotong University, 2007.
3 杨轲. 磁悬浮列车仿真平台设计及运控算法研究[D]. 杭州:浙江大学电气工程学院, 2008.
YangKe. Research on maglev train simulation platform design and operation and control algorithm[D]. Hanzhou: College of Electrical Engineering，Zhejiang University, 2008.
4 IchikawaK. Application of optimization theory for bounded state variable problems to the operation of a train[J]. Bulletin of Japanese Society of Mechanical Engineering，1968, 11(47): 857⁃865.
5 MilroyI P. Aspects of automatic train control[D]. Loughborough：Loughborough University, 1980.
6 AsnisI A, DmitrukA V, OsmolovskiiN P. Solution of the problem of the energetically optimal control of the motion of a train by the maximum principle[J]. USSR Computational Mathematics and Mathematical Physics, 1985, 25(6): 37⁃44.
7 KhmelnitskyE. On an optimal control problem of train operation[J]. IEEE Transactions on Automatic Control, 2000, 45(7):1257⁃1266.
8 HowlettP. The optimal control of a train[J]. Annals of Operations Research, 2000, 98(1⁃4):65⁃87.
9 DongH, ZhangL, ChenY, et al. Multi⁃objective train trajectory design based on dynamic programming[C]∥The 33rd Chinese Control Conference (CCC), Nanjing, China, 2014: 9060⁃9065.
10 XuY, ZhaoX, WangL, et al. Optimal control of automatic train operation based on multi⁃scale dynamic programming[C]∥The 33rd Chinese Control Conference (CCC), Nanjing, China, 2014: 3429⁃3433.
11 LuS, HillmansenS, HoT K, et al. Single⁃train trajectory optimization[J]. IEEE Transactions on Intelligent Transportation Systems, 2013, 14(2): 743⁃750.
12 刘进, 吴汶麒. 高速磁悬浮交通二维速度防护曲线及其算法研究[J]. 中国铁道科学, 2002, 23(4):106⁃110.
LiuJin, WuWen⁃lin. Research on 2⁃D speed protection curve and its algorithm of high⁃speed maglev transportation[J]. China Railway Science, 2002, 23(4):106⁃110.
13 江亚, 吴汶麒, 刘进. 磁悬浮列车运行控制系统二维速度防护曲线仿真[J]. 同济大学学报：自然科学版, 2004, 32(3):397⁃400.
JiangYa, WuWen⁃lin, LiuJin, et al. Simulation of high⁃speed maglev train 2⁃D speed protection curve[J]. Journal of Tongji University(Natural Science), 2004, 32(3):397⁃400.
14 杨光, 唐祯敏. 高速磁悬浮列车的安全速度防护问题研究[J]. 北京交通大学学报, 2007, 31(2):38⁃42.
YangGuang, TangZhen⁃min. Study on safety speed protection of the high maglev train[J]. Journal of Beijing Jiaotong University, 2007, 31(2):38⁃42.
15 HowardR A. Dynamic programming[J]. Management Science, 1966, 12(5):317⁃348.
[1] 尹紫红, 朱波, 邵国霞, 孔德惠, 蒋良潍. 铁路超重货物作用下的轨道路基响应[J]. 吉林大学学报(工学版), 2017, 47(5): 1446-1452.
[2] 左静, 帅斌, 黄文成. 改进距离熵权MULTIMOORA的铁路应急救援方案搜索[J]. 吉林大学学报(工学版), 2017, 47(4): 1068-1074.
[3] 牛治慧, 苏建, 张益瑞, 徐观, 谭富星. 基于转向架试验台的轨道不平顺模拟试验[J]. 吉林大学学报(工学版), 2017, 47(2): 400-407.
[4] 王启明, 苏建, 张兰, 陈秋雨, 徐观. 基于L-M算法的正交Stewart平台位姿正解的初值补偿[J]. 吉林大学学报(工学版), 2017, 47(1): 97-104.
[5] 张益瑞, 苏建, 张兰, 谭富星, 徐观. 轨道车辆转向架一系悬挂刚度测定[J]. 吉林大学学报(工学版), 2016, 46(4): 1083-1089.
[6] 刘玉梅, 赵聪聪, 熊明烨, 郭文翠, 张志远. 基于物元模型的高速轨道车辆传动系可靠性评价[J]. 吉林大学学报(工学版), 2015, 45(4): 1063-1068.
[7] 石怀龙, 宋烨, 邬平波, 曾京, 朱海燕. 高速动车组转向架悬挂刚度特性[J]. 吉林大学学报(工学版), 2015, 45(3): 776-782.
[8] 王秀刚, 苏建, 曹晓宁, 徐振, 卢海隔, 田宗举. 基于旋转矩阵正交性的转向架6自由度平台位姿正解解算[J]. 吉林大学学报(工学版), 2013, 43(05): 1241-1246.
[9] 曹晓宁, 刘玉梅, 苏建, 王秀刚, 李卓. 转向架质心高度的测定[J]. 吉林大学学报(工学版), 2013, 43(02): 329-333.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
版权所有 © 《吉林大学学报(工学版)》编辑部
地址：长春市人民大街5988号　电话：+86-431-85095297　传真：+86-431-85094074　E-mail: xbgxb@jlu.edu.cn
本系统由北京玛格泰克科技发展有限公司设计开发