吉林大学学报(工学版) ›› 2020, Vol. 50 ›› Issue (1): 202-209.doi: 10.13229/j.cnki.jdxbgxb20181138
• 交通运输工程·土木工程 • 上一篇
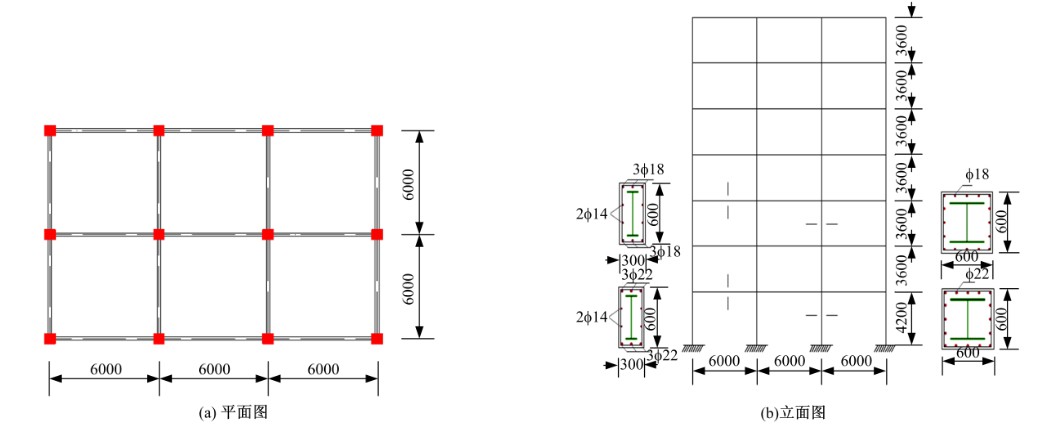
考虑楼层相关性的框架结构地震易损性分析
- 1. 西南交通大学 土木工程学院,成都 610031
2. 宁夏大学 土木与水利工程学院,银川 750021
3. 太原理工大学 建筑与土木工程学院,太原 030024
Seismic vulnerability analysis of frame structure considering floor correlation
Xiu-zhen WANG1,2( ),Yong-jiu QIAN1(
),Yong-jiu QIAN1( ),Chang-jiang SHAO1,Shuai SONG3
),Chang-jiang SHAO1,Shuai SONG3
- 1. School of Civil Engineering,Southwest Jiaotong University,Chengdu 610031,China
2. School of Civil Engineering and Hydraulic Engineering,Ningxia University,Yinchuan 750021,China
3. School of Architecture and Civil Engineering,Taiyuan University of Technology, Taiyuan 030024,China
摘要:
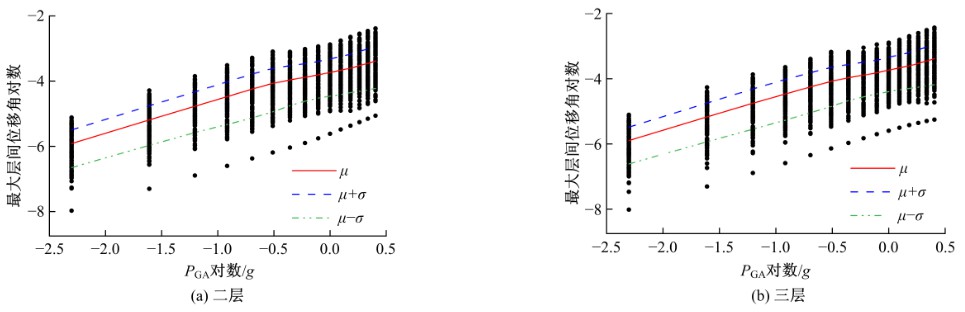
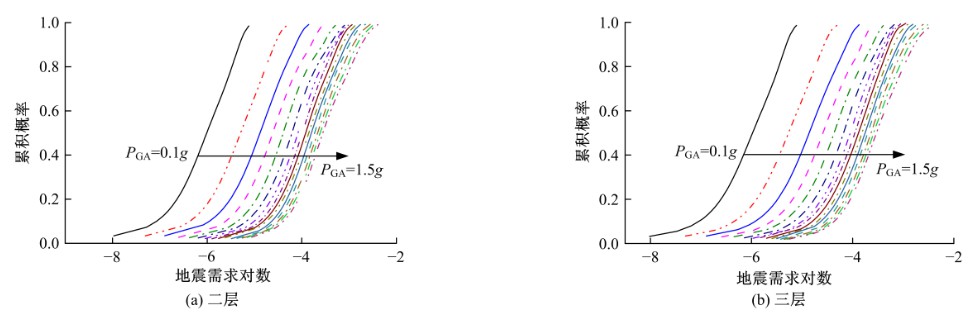
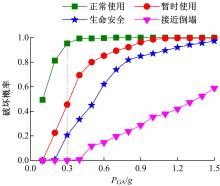
为了在框架结构易损性分析中考虑各楼层地震需求之间相关性的影响,提出了考虑各楼层地震需求相关性的框架结构易损性分析方法。采用多元Copula函数方法求出各楼层地震需求的联合分布函数,得到框架结构的易损性曲线,并与一阶界限法和Bootstrap重抽样法的分析结果进行了对比。结果表明:采用本文的框架结构易损性分析方法得到的结果,均位于一阶界限法两个界限之间,且与Bootstrap重抽样法的结果吻合较好,这一定程度上证明了本文方法的准确性。
中图分类号:
- TU375
| 1 | 王丹 . 钢框架结构的地震易损性及概率风险分析[D]. 哈尔滨: 哈尔滨工业大学土木工程学院, 2006. |
| Wang Dan . Seismic fragility analysis and probabilistic risk analysis of steel frame structures[D]. Harbin: School of Civil Engineering, Harbin Institute of Technology, 2006. | |
| 2 | Gardoni P , Kiureghian A D , Mosalam K M . Probabilistic capacity models and fragility estimates for reinforced concrete columns based on experimental observations[J]. Journal of Engineering Mechanics, 2002, 128(10): 1024-1038. |
| 3 | Shinozuka M , Feng M Q , Lee J , et al . Statistical analysis of fragility curves[J]. Journal of Engineering Mechanics, 2000, 126(12): 1224-1231. |
| 4 | 吕大刚, 宋鹏彦, 于晓辉, 等 . 结构动力抗震可靠度理论的研究进展[J]. 西南交通大学学报, 2015, 50(6): 1025-1038. |
| Lv Da-gang , Song Peng-yan , Yu Xiao-hui , et al . Research progress of structural dynamic seismic reliability theory[J]. Journal of Southwest Jiaotong University, 2015, 50(6): 1025-1038. | |
| 5 | 吕大刚, 于晓辉, 陈志恒 . 钢筋混凝土框架结构侧向倒塌地震易损性分析[J]. 哈尔滨工业大学学报, 2011, 43(6): 1-5. |
| Lv Da-gang , Yu Xiao-hui , Chen Zhi-heng . Seismic vulnerability analysis of reinforced concrete frame structures subjected to lateral collapse[J]. Journal of Harbin Institute of Technology, 2011, 43 (6): 1-5. | |
| 6 | 宋帅, 钱永久, 吴刚 . 基于Copula函数的桥梁系统地震易损性方法研究[J]. 工程力学, 2016, 33(11): 193-200. |
| Song Shuai , Qian Yong-jiu , Wu Gang . Study on seismic vulnerability of bridge system based on Copula function[J]. Engineering Mechanics, 2016, 33(11): 193-200. | |
| 7 | Hong H P , Zhou W , Zhang S , et al . Optimal condition-based maintenance decisions for systems with dependent stochastic degradation of components[J]. Reliability Engineering and System Safety, 2014, 121: 276-288. |
| 8 | 李鹏举, 朱辉 . 基于Copula函数的金融理财产品风险度量[J]. 系统工程理论与实践, 2014, 34(3): 663-667. |
| Li Peng-ju , Zhu Hui . Risk measurement of financial products based on Copula function[J]. System Engineering Theory and Practice, 2014, 34 (3): 663-667. | |
| 9 | 张英芝, 刘津彤, 申桂香, 等 . 基于故障相关性分析的数控机床系统可靠性建模[J]. 吉林大学学报:工学版, 2017, 47(1): 169-173. |
| Zhang Ying-zhi , Liu Jin-tong , Shen Gui-xiang , et al . Reliability modeling of CNC machine tools system based on failure correlation analysis[J]. Journal of Jilin University (Engineering and Technology Edition), 2017, 47(1): 169-173. | |
| 10 | 张英芝, 郑锐, 申桂香, 等 . 基于COPULA理论的数控装备故障相关性[J]. 吉林大学学报:工学版, 2011, 41(6): 1636-1640. |
| Zhang Ying-zhi , Zheng Rui , Shen Gui-xiang , et al . Failure dependency of CNC equipment based on copula theory[J]. Journal of Jilin University (Engineering and Technology Edition), 2011, 41(6): 1636-1640. | |
| 11 | 曹晋华, 程侃 . 可靠性数学引论[M]. 北京:高等教育出版社, 2012. |
| 12 | 刘月飞 . 考虑失效模式和验证模式相关性的桥梁结构体系可靠度分析[D]. 哈尔滨: 哈尔滨工业大学土木工程学院, 2015. |
| Liu Yue-fei . Reliability analysis of bridge structural system considering failure mode and verification mode correlation [D]. Harbin:School of Civil Engineering, Harbin Institute of Technology, 2015. | |
| 13 | Mirza S A , Macgregor J G . Variability of mechanical properties of reinforced bars[J]. Journal of Structural Division, 1979, 105(5): 921-937. |
| 14 | Mirza S A , Hatzinikolas M , Macgregor J G . Statistical descriptions of strength of concrete[J]. Journal of the Structural Division, 1979, 105(6): 1021-1037. |
| 15 | GB50010―2010. 钢筋混凝土结构设计规范[S]. |
| 16 | Porter K A , Beck J L , Shaikhutdinov R V . Sensitivity of building loss estimates to major uncertain variables[J]. Earthquake Spectra, 2002, 18(4):719-743. |
| 17 | Nielson B , Pang W . Effect of ground motion suite size on uncertainty estimation in seismic bridge fragility modeling[C]∥Structures Congress 2011 of ASCE, Las Vegas, Nevada, United States, 2011: 23-34. |
| 18 | 陈波 . 结构非线性动力分析中地震动记录的选择和调整方法研究[D]. 北京: 中国地震局地球物理研究所, 2014. |
| Chen Bo .Ground motion selection and modification methods for performing nonlinear dynamic analysis of buildings[D]. Beijing: Institute of Geophysics, China Seismological Bureau, 2014. | |
| 19 | GB50011―2010. 建筑抗震设计规范[S]. |
| 20 | 王秋维, 史庆轩, 杨坤 . 型钢混凝土结构抗震性态水平和容许变形值的研究[J]. 西安建筑科技大学学报:自然科学版, 2009, 41(1): 82-87. |
| Wang Qiu-wei , Shi Qing-xuan , Yang Kun . Research on the seismic behavior and admissible deformation of steel reinforced concrete structures [J]. Journal of Xi'an University Of Architecture and Technology (Natural Science Edition), 2009, 41(1): 82-87. | |
| 21 | Scaillet O , Fermanian J D . Nonparametric estimation of copulas for time series[J]. Journal of Risk, 2003, 5(3): 25-54. |
| 22 | 谢中华 . MATLAB统计分析与应用: 40个案例分析[M]. 北京: 北京航空航天大学出版社, 2012. |
| 23 | 胡云昌, 郭振邦 . 结构系统可靠性分析原理及应用[M].天津: 天津大学出版社, 1992. |
| 24 | Lee H K H . Elements of computational statistics[J]. Journal of the American Statistical Association, 2003, 98(463): 772-773. |
| [1] | 舒浩, 史江义, 马佩军, 潘伟涛, 杨林安. 基于花环网络的偏转直通片上网络框架结构[J]. 吉林大学学报(工学版), 2017, 47(3): 988-995. |
| [2] | 姜封国, 赵景鲁, 郑重远. 基于荷载抗力设计法的受火钢柱可靠性分析[J]. 吉林大学学报(工学版), 2014, 44(4): 978-984. |
| [3] | 张立业, 郭学东, 董丽娟. 载荷共享过程的桥梁系统首次失效平均时间[J]. 吉林大学学报(工学版), 2013, 43(05): 1247-1252. |
| [4] | 郭学东, 张立业, 董丽娟, 吴云涛, 张强. 桥梁系统可靠性评估方法 [J]. , 2012, (03): 634-638. |
| [5] | 姜浩, 郭学东, 张立业. 基于模态应变能理论的混凝土结构损伤诊断[J]. 吉林大学学报(工学版), 2010, 40(增刊): 209-0213. |
| [6] | 潘明远, 姚继涛. 钢筋混凝土结构构件的可靠性[J]. 吉林大学学报(工学版), 2010, 40(增刊): 218-0221. |
| [7] | 潘明远, 姚继涛, 崔旸. 钢筋混凝土矩形截面柱绕丝加固的受力性能[J]. 吉林大学学报(工学版), 2009, 39(04): 932-936. |
| [8] | 施刚,石永久,王元清. 钢结构梁柱连接节点域剪切变形计算方法[J]. 吉林大学学报(工学版), 2006, 36(04): 462-466. |
| [9] | 施刚,石永久,王元清. 钢框架半刚性端板连接弯矩-转角滞回模型[J]. 吉林大学学报(工学版), 2005, 35(06): 654-0660. |
| [10] | 刘寒冰, 王 磊, 王延华. 桥梁曲面实体建模几何对象模型[J]. 吉林大学学报(工学版), 2005, 35(01): 61-0064. |
| [11] | 张延年, 刘 斌 , 朱朝艳 , 郭鹏飞. 工程结构优化设计的改进混合遗传算法[J]. 吉林大学学报(工学版), 2005, 35(01): 65-0069. |
|
||