互质圆形阵列DOA估计方法

doi:10.13229/j.cnki.jdxbgxb20200794

摘要/Abstract

摘要：

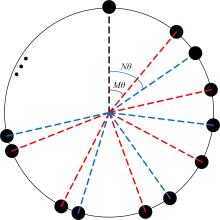
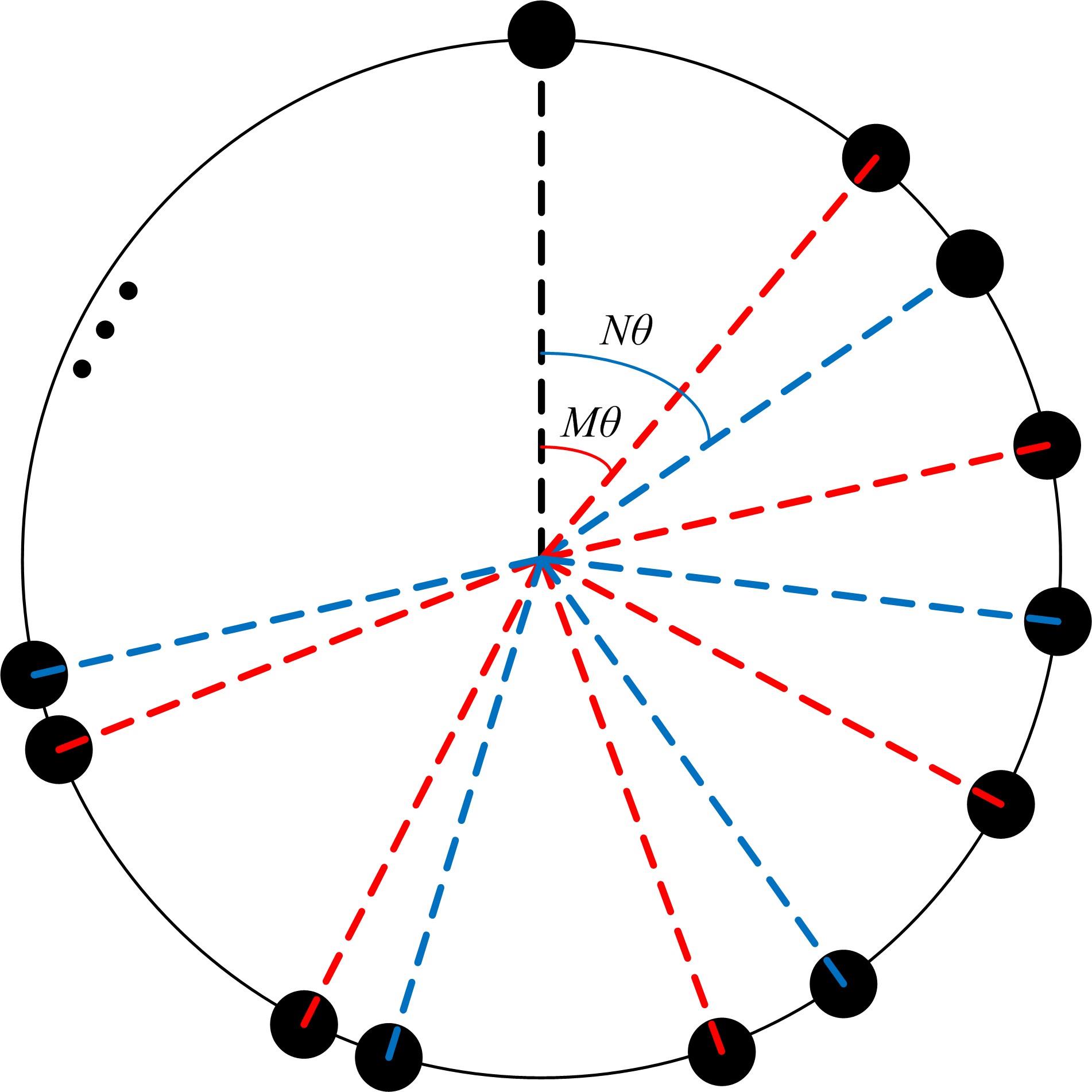
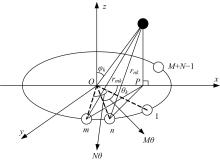
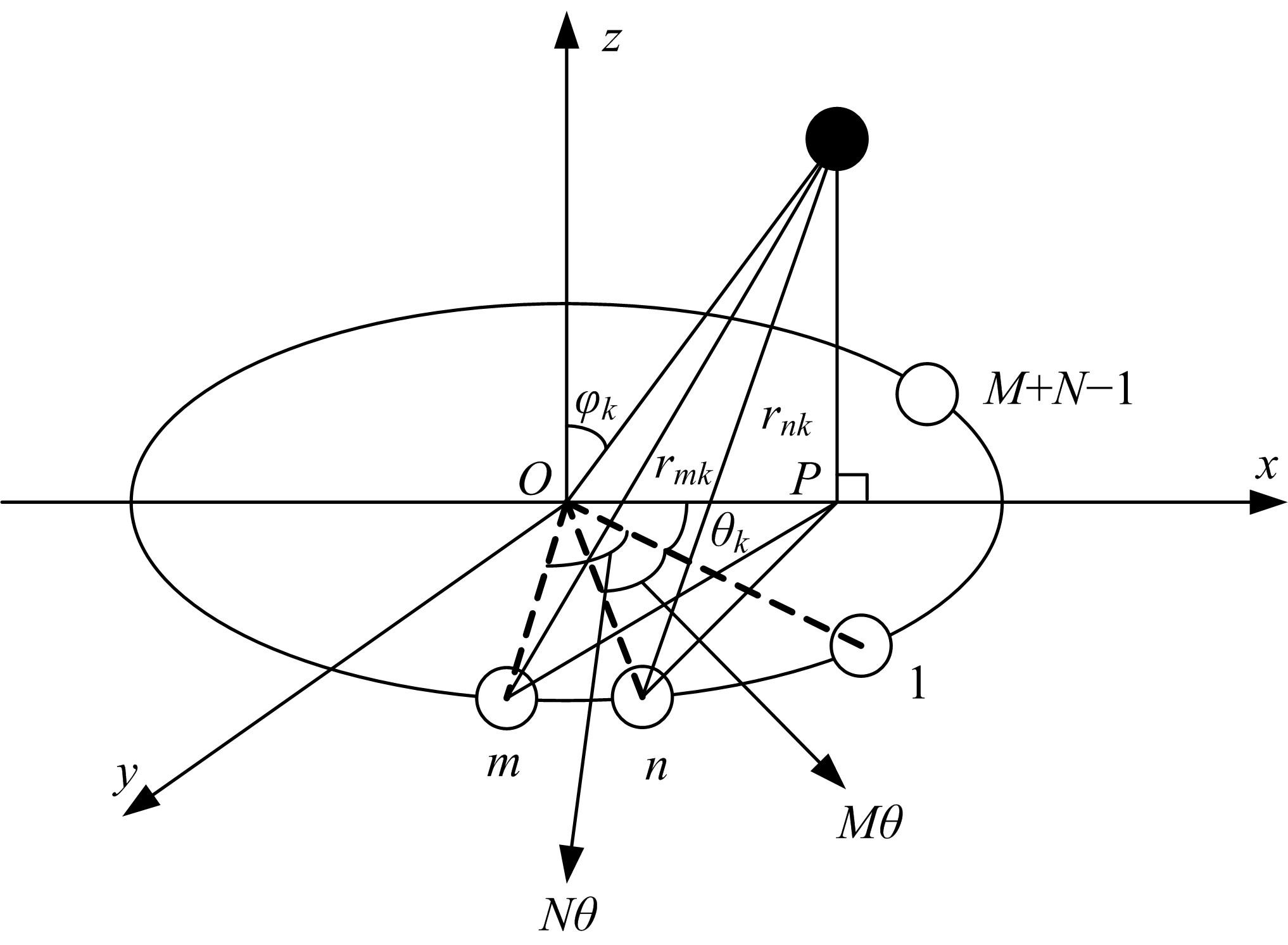
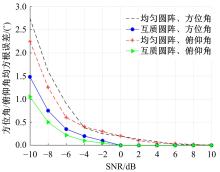
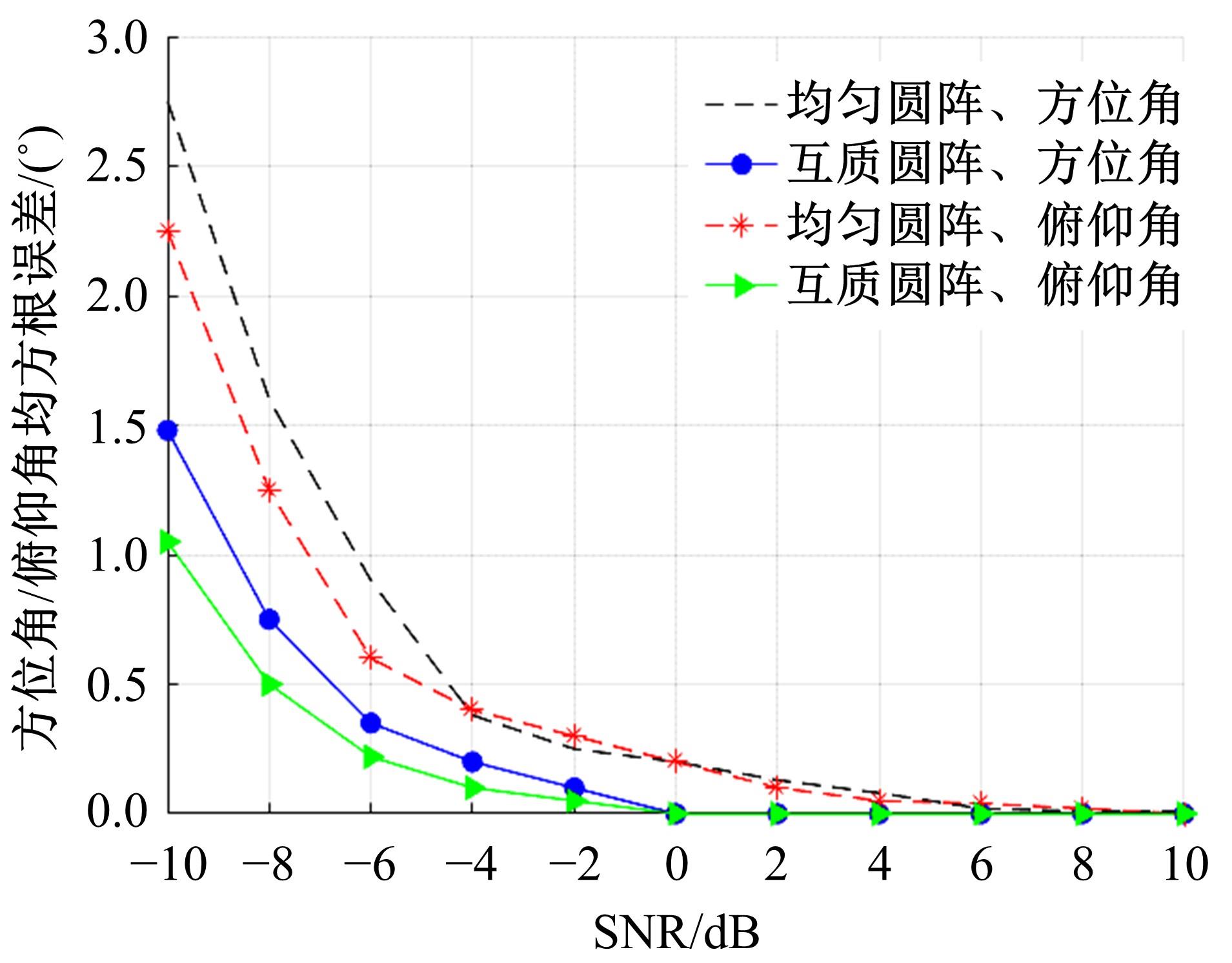
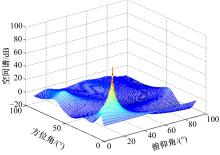
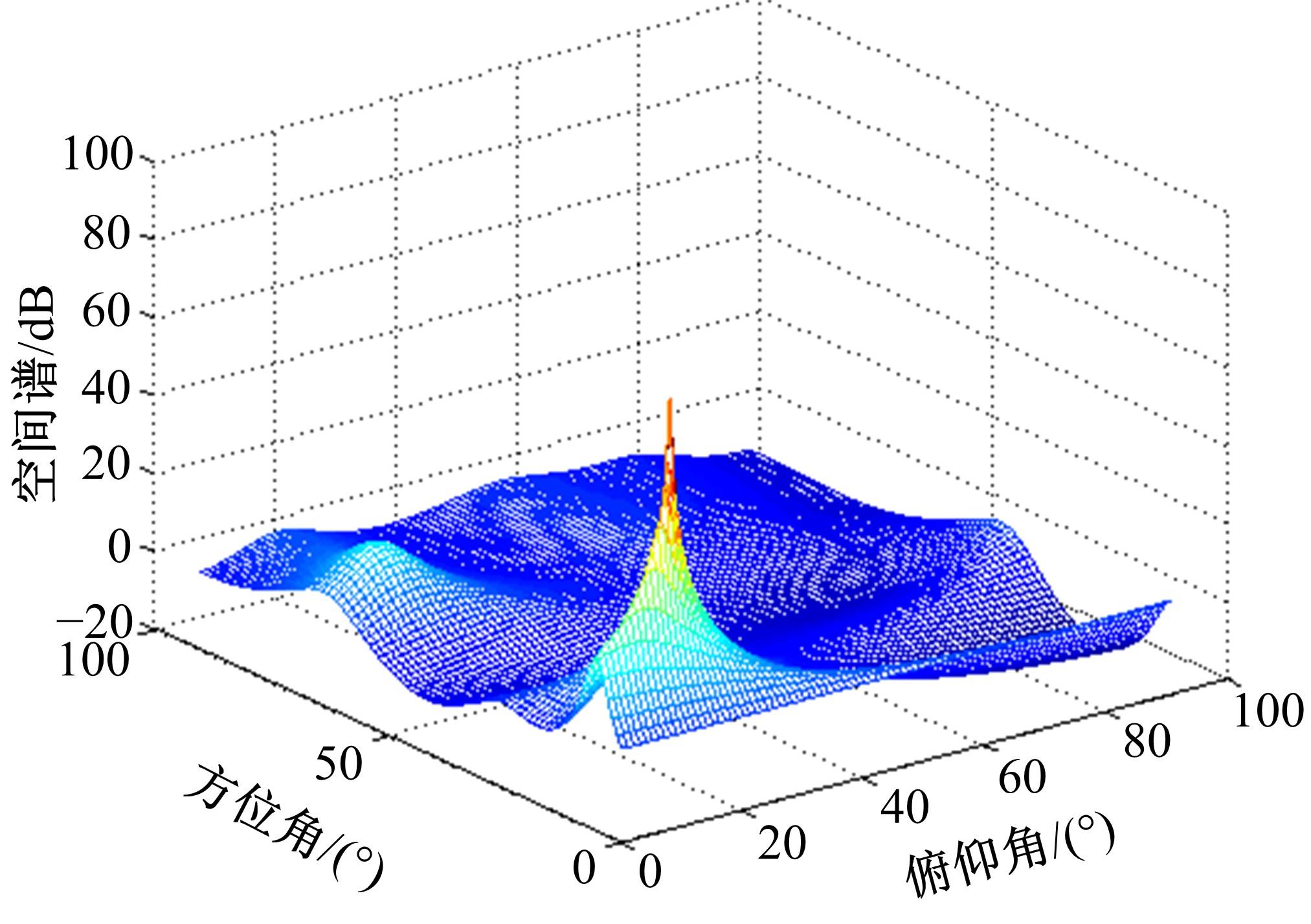
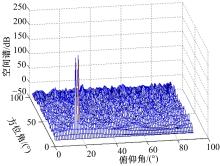
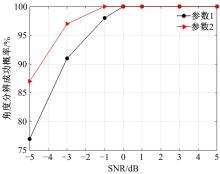
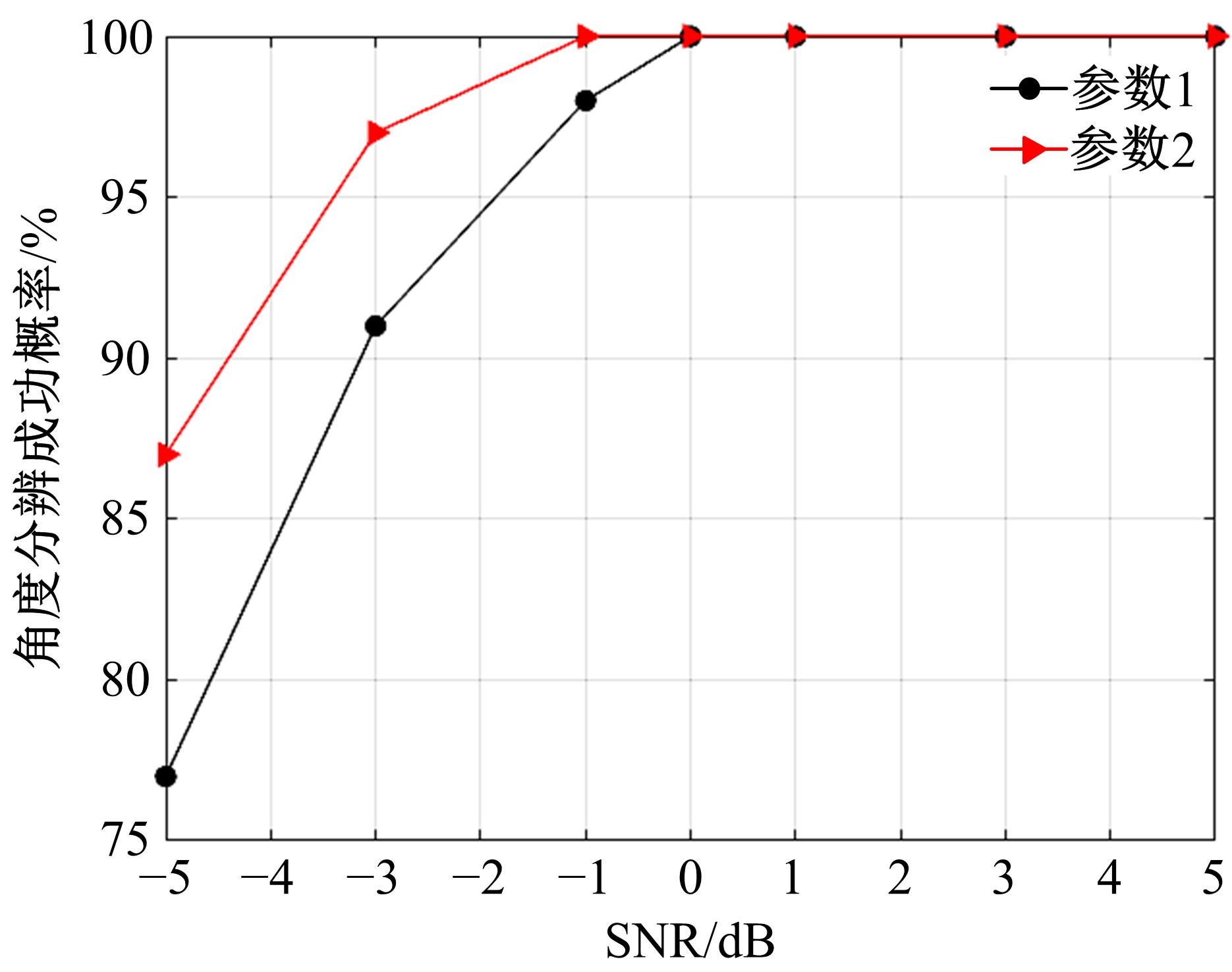
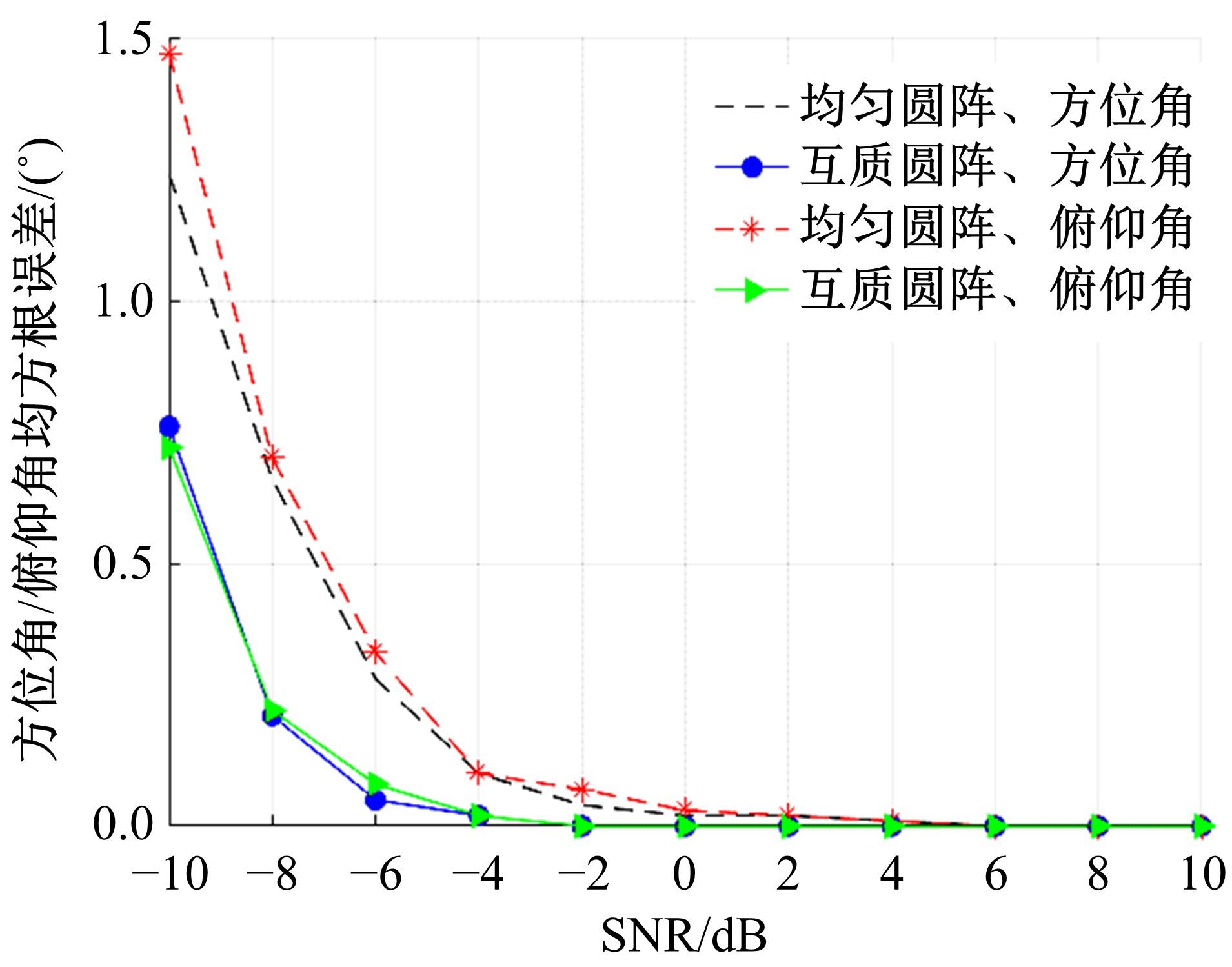
针对传统均匀圆形阵列孔径受限的问题，设计了一种互质圆形阵列，并在此基础上，研究了一种基于相位模式激励的二维波达方向估计方法。首先利用两个均匀圆形子阵列进行堆叠形成互质圆形阵列结构。然后，基于相位模式变换算法将元素空间问题转化到波束空间，将互质圆形阵列合成类似于 ULA 的范德蒙结构且中心埃尔米特对称的阵列流型，减小谱峰搜索维度。最后，通过酉变换实现阵列流型的实数化，降低算法复杂度。理论分析和仿真实验表明：在相同条件下，相比于均匀圆形阵列MUSIC算法，所提互质圆形阵列相位模式激励MUSIC算法的运行时间从1.825 s降至0.622 s，阵列孔径增大MN/（M+N-2）倍，具备更高的波达方向估计精度和系统实时性，并对相近源具有较高的估计分辨率。

关键词: DOA估计, 互质圆形阵列, MUSIC算法, 相位模式激励

Abstract:

To solve the problem of limited aperture of traditional uniform circular arrays， a co-prime circular array is designed， and on this basis， a two-dimensional direction of arrival estimation method based on phase mode excitation is studied. First， two uniform circular sub-arrays with a distance between array elements greater than half a wavelength are stacked to form a relatively prime circular array structure. Then， based on the phase mode transformation algorithm， the element space problem is transformed into the beam space. The algorithm combines the co-prime circular array into a Vandermonde structure similar to ULA and the Hermitian center symmetrical array flow pattern， reducing the dimensions of spectral peak searching， realizing array flow pattern through unitary transformation， reducing algorithm complexity. Theoretical analysis and simulation experiments show that under the same conditions， compared with the uniform circular array MUSIC algorithm， the proposed phase mode excitation MUSIC algorithm for the relatively prime circular array reduces the running time from 1.825 s to 0.622 s， increases the array aperture MN/（M+N-2） times， improves the DOA estimation accuracy and the real-time performance of the system， and it has a higher resolution for the estimation of similar sources.

Key words: DOA estimation, coprime circular array, MUSIC algorithm, phase mode excitation

中图分类号:

TN911

李新波,王晓玉,李厚禹,姜良旭,关博,王旺. 互质圆形阵列DOA估计方法[J]. 吉林大学学报(工学版), 2022, 52(1): 204-210.

Xin-bo LI,Xiao-yu WANG,Hou-yu LI,Liang-xu JIANG,Bo GUAN,Wang WANG. Coprime circular array DOA estimation method[J]. Journal of Jilin University(Engineering and Technology Edition), 2022, 52(1): 204-210.

图/表 10

图1

图2

图3

图4

图5

表1

图6

图7

图8

图9

参考文献 22

1	单泽彪, 刘小松, 王春阳, 等. 多快拍加权平滑范数DOA估计[J]. 光学精密工程, 2017, 25(10s): 167-173.
	Shan Ze-biao, Liu Xiao-song, Wang Chun-yang, et al. Multi-shot weighted smoothing norm DOA estimation[J]. Opt Precision Eng, 2017, 25(10s): 167-173.
2	李新波, 姜良旭, 刘国君, 等. 用于声矢量阵列目标波达方向跟踪的粒子滤波算法[J]. 光学精密工程, 2015, 23(10z): 605-612.
	Li Xin-bo, Jiang Liang-xu, Liu Guo-jun, et al. Particle filter algorithm for tracking the direction of arrival of acoustic vector array targets[J]. Opt Precision Eng, 2015, 23(10z): 605-612.
3	赵洋, 李新波, 石要武. 声矢量阵列波达方向估计的四元数空间稀疏分解[J]. 光学精密工程, 2018, 26(3): 715-722.
	Zhao Yang, Li Xin-bo, Shi Yao-wu. Sparse decomposition of quaternion space for direction of arrival estimation of acoustic vector array[J]. Opt Precision Eng, 2018, 26(3): 715-722.
4	张小飞, 林新平, 郑旺, 等. 互质阵中空间谱估计研究进展[J]. 南京航空航天大学学报, 2017, 49(5): 635-644.
	Zhang Xiao-fei, Lin Xin-ping, Zheng Wang, et al. Research progress of spatial spectrum estimation in coprime arrays[J]. Journal of Nanjing University of Aeronautics and Astronautics, 2017, 49(5): 635-644.
5	Vaidyanathan P P, Pal P. Sparse Sensing With Co-Prime Samplers and Arrays[J]. IEEE Transactions on Signal Processing, 2011, 59(2): 573-586.
6	Vaidyanathan P P, Pal P. Theory of Sparse Coprime Sensing in Multiple Dimensions[J]. IEEE Transactions on Signal Processing, 2011, 59(8): 3592-3608.
7	张彦奎, 许海韵, 巴斌, 等. 基于互质阵列重构的高维波达方向估计算法[J]. 电子学报, 2018, 46(12): 2923-2929.
	Zhang Yan-kui, Xu Hai-yun, Ba Bin,et al. High-dimensional DOA estimation algorithm based on coprime array reconstruction[J]. Electronic Journal, 2018, 46(12): 2923-2929.
8	Wang X M, Wang X. Hole identification and filling in k-times extended co-prime arrays for highly efficient DOA estimation[J]. IEEE Transactions on Signal Processing, 2019, 67(10): 2693-2706.
9	周成伟, 郑航, 顾宇杰, 等. 互质阵列信号处理研究进展:波达方向估计与自适应波束成形[J]. 雷达学报, 2019, 8(5):558-577.
	Zhou Cheng-wei, Zheng Hang, Gu Yu-jie, et al. Research progress of coprime array signal processing: direction of arrival estimation and adaptive beamforming[J]. Journal of Radar, 2019, 8(5):558-577.
10	金强, 汤亚鸽, 杨明. 基于互质阵列的时延和到达角度联合估计算法[J]. 科技创新与应用, 2019(24): 140-141.
	Jin Qiang, Tang Ya-ge, Yang Ming. Joint estimation algorithm of time delay and angle of arrival based on coprime array[J]. Technological Innovation and Application, 2019(24): 140-141.
11	Zhou C, Gu Y, He S, et al. A robust and efficient algorithm for coprime array adaptive beamforming[J]. IEEE Transactions on Vehicular Technology, 2018, 67(2): 1099-1112.
12	di Martino G, Iodice A. Passive beamforming with coprime arrays[J]. Radar, Sonar & Navigation, 2017, 11(6): 964-971.
13	Li J, Li D, Jiang D, et al. Extended-aperture unitary root MUSIC-Based DOA estimation for coprime array[J]. IEEE Communications Letters, 2018, 22(4): 752-755.
14	Elbir A M. L-shaped coprime array structures for DOA estimation[J]. Multidimensional Systems & Signal Processing, 2019,28(9):205-219.
15	Zhang Zhi, Guo Yu, Huang Yu-zheng, et al. A 2-D DOA estimation method with reduced complexity in unfolded coprime L-shaped array[J]. IEEE Systems Journal, 2021,15(1):407-410.
16	Hui Z, Zhang X F, Wang Z, et al. DOA estimation of noncircular signals for unfolded coprime linear array: identifiability, DOF and algorithm[J]. IEEE Access, 2018, 6: 29382-29390.
17	Wang Z, Zhang X F, Pan G, et al. DOA estimation for coprime linear arrays: an ambiguity-free method involving full DOFs[J]. IEEE Communications Letters, 2018, 22(3): 562-565.
18	孙兵, 阮怀林, 吴晨曦, 等. 基于Toeplitz协方差矩阵重构的互质阵列DOA估计方法[J]. 电子与信息学报, 2019, 41(8): 1924-1930.
	Sun Bing, Ruan Huai-lin, Wu Chen-xi, et al. Coprime array DOA estimation method based on Toeplitz covariance matrix reconstruction[J]. Journal of Electronics and Information,2019, 41(8): 1924-1930.
19	安云飞. 基于均匀圆阵的MUSIC快速测向算法研究[D]. 哈尔滨: 哈尔滨工程大学信息与通信工程学院, 2014.
	An Yun-fei. Research on MUSIC fast direction finding algorithm based on uniform circular array[D]. Harbin: College of Information and Communication Engineering,Harbin Engineering University, 2014.
20	王芳, 闫哲, 罗景青. 基于模式空间变换的宽带波束形成方法[J]. 计算机工程与应用, 2011, 47(17): 128-130.
	Wang Fang, Yan Zhe, Luo Jing-qing. Broadband beam forming method based on mode space transformation[J]. Computer Engineering and Applications, 2011, 47(17): 128-130.
21	张小飞. 阵列信号处理的理论与应用[M]. 北京:国防工业出版社, 2013.
22	闫金山, 彭秀艳, 王成鹏. 基于酉变换的虚拟阵列DOA估计算法[J]. 哈尔滨工业大学学报, 2012, 44(4): 136-140.
	Yan Jin-shan, Peng Xiu-yan, Wang Cheng-peng. Virtual array DOA estimation algorithm based on unitary transformation[J]. Journal of Harbin Institute of Technology, 2012, 44(4): 136-140.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

[1]	李新波, 孙海欣, 李晓青, 赵洋, 梁亮, 房小朋. 基于四元数MUSIC算法的声矢量传感器阵列二维波达角估计[J]. 吉林大学学报(工学版), 2014, 44(5): 1453-1459.
[2]	司伟建, 吴迪, 陈涛. 基于部分重合信号的空间谱估计新方法[J]. 吉林大学学报(工学版), 2014, 44(2): 490-496.
[3]	王茂林,刘少伟,孙晓东. 复杂噪声背景下正弦频率估计新方法[J]. 吉林大学学报(工学版), 2009, 39(增刊2): 371-0375.
[4]	孙晓东, 石要武, 于晓辉. 混沌干扰背景下的正弦频率估计新方法[J]. 吉林大学学报(工学版), 2009, 39(05): 1353-1357.
[5]	周欣，石要武，郭宏志 . 多径信号的二维DOA和极化参数同时估计算法[J]. 吉林大学学报(工学版), 2009, 39(03): 797-0802.
[6]	魏小丽，陈建，林琳 . 基于空间平滑算法的二维相干源DOA估计[J]. 吉林大学学报(工学版), 2008, 38(05): 1160-1164.
[7]	黄家才，石要武，周欣 . 基于四阶累积量的极化近场源距离、频率及到达角的联合估计算法[J]. 吉林大学学报(工学版), 2006, 36(06): 973-0977.
[8]	石宇，王树勋，黄志强 . 基于多级维纳滤波器的信源参数估计[J]. 吉林大学学报(工学版), 2006, 36(05): 761-0765.
[9]	刘若伦, 王树勋. 二维DOA估计的高分辨阵列(HRA)[J]. 吉林大学学报(工学版), 2000, 30(01): 90-94.