吉林大学学报(工学版) ›› 2022, Vol. 52 ›› Issue (4): 950-958.doi: 10.13229/j.cnki.jdxbgxb20211034
• 通信与控制工程 • 上一篇
基于SESTH的线性调频连续波激光雷达信号时延估计
- 1.长春理工大学 电子信息工程学院,长春 130022
2.白城师范学院 机械与控制工程学院,吉林 白城 137000
3.西安工业大学 西安市主动光电成像探测技术重点实验室,西安 710021
Time delay estimation of linear frequency-modulated continuous-wave lidar signals via SESTH
Xue-mei LI1,2( ),Chun-yang WANG1,3(
),Chun-yang WANG1,3( ),Xue-lian LIU3,Da XIE1
),Xue-lian LIU3,Da XIE1
- 1.School of Electronic and Information Engineering,Changchun University of Science and Technology,Changchun 130022,China
2.School of Mechanical and Control Engineering,Baicheng Normal University,Baicheng 137000,China
3.Xi'an Key Laboratory of Active Photoelectric Imaging Detection Technology,Xi'an Technological University,Xi'an 710021,China
摘要:
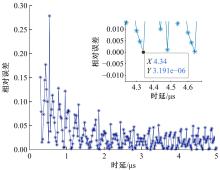
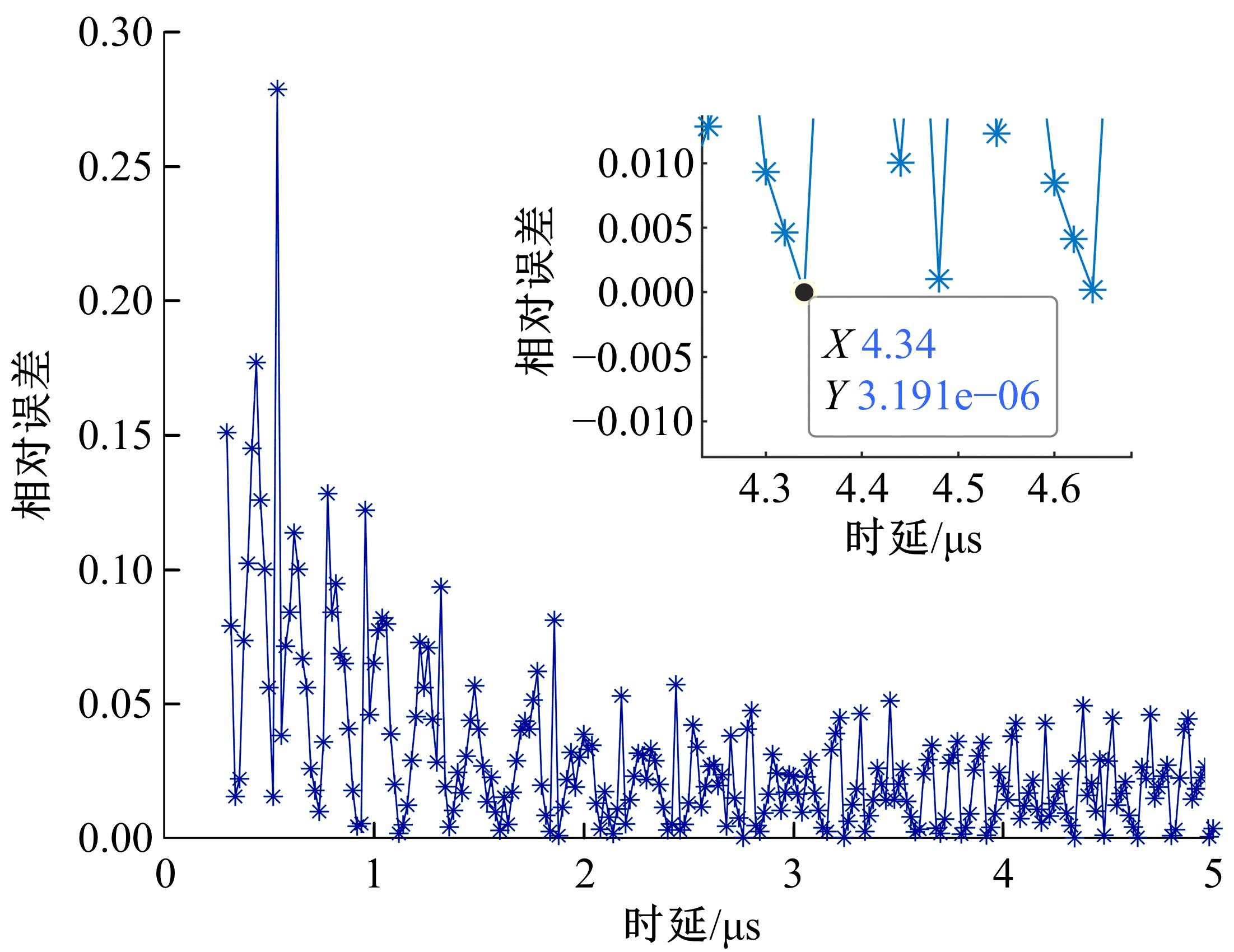
针对线性调频连续波(Linear frequency-modulated continuous-wave,LFMCW)激光雷达低信噪比下目标回波信号参数难以提取的问题,提出了一种基于SESTH(Synchroextracting S transform based on Hough transform)变换的信号时延估计方法。首先,融入Hough变换,构建了Chirp信号的SESTH变换模型。然后,推导出Chirp信号的初始频率和调频率参数估计模型。最后,利用LFMCW激光雷达发射信号与回波信号的时频特性,构建Chirp信号的时延估计模型,有效解算出目标与雷达间的相对距离。为验证本文算法的有效性,进行了仿真对比分析。结果表明:本文SESTH算法在时延为4.34 μs时,相对误差最小值为3.191×10-6;在
中图分类号:
- TN911.7
| 1 | Chimenti R V, Dierking M P, Powers P E, et al. Sparse frequency LFM ladar signals[J]. Optics Express, 2009, 17(10): 8302-8309. |
| 2 | Tsuchida H. Regression analysis of FMCW-LiDAR beat signals for non-linear chirp mitigation[J]. Electronics Letters, 2019, 55(16): 914-916. |
| 3 | Sharma K K, Joshi S D. Time delay estimation using fractional Fourier transform[J]. Signal Processing, 2007, 87(5): 853-865. |
| 4 | 宋杰, 唐小明, 何友. 脉冲制无源雷达动目标时延快速估计方法[J].电子科技大学学报, 2009, 38(6): 908-912, 978. |
| Song Jie, Tang Xiao-ming, He You. Fast method for time delay estimation of moving targets in passive pulse radar systems[J]. Journal of University of Electronic Science and Technology of China, 2009, 38(6): 908-912, 978. | |
| 5 | Riemensberger Johann, Lukashchuk Anton, Karpov Maxim, et al. Massively parallel coherent laser ranging using a soliton microcomb[J]. Nature, 2020, 581(7807): 164-170. |
| 6 | Xu Zhong-yang, Zhang Hong-xiang, Chen Kai, et al. FMCW LiDAR using phase-diversity coherent detection to avoid signal aliasing[J]. IEEE Photonics Technology Letters, 2019, 31(22): 1822-1825. |
| 7 | Fardoost A, Vanani F G, Wen H, et al. Few-mode frequency-modulated LiDAR receivers[J]. Optics Letters, 2020,45(11): 3127-3130. |
| 8 | 戴延中, 李志舜. 基于Wigner-Ville分布的宽带回波到达时刻估计方法[J]. 声学学报, 2002, 27(1): 84-87. |
| Dai Yan-zhong, Li Zhi-shun. Time of arrival estimation of wide band echoes based on wignerville distribution[J]. Acta Acustica, 2002, 27(1): 84-87. | |
| 9 | 蒋忠进, 林君, 陈祖斌. 离散小波变换在Chirp信号检测与时延估计中的应用[J]. 自动化仪表, 2003, 43(2): 58-61. |
| Jiang Zhong-jin, Lin Jun, Chen Zu-bin. The application of discrete small wave transfer in chirp signal detection and delay estimation[J]. Process Automation Instrumentation, 2003, 43(2): 58-61. | |
| 10 | 陆侃, 卓永宁. UWB CHIRP信号的多径时延频域提取方法[J]. 通信技术, 2010, 43(12): 15-17. |
| Lu Kan, Zhou Yong-ning. Extraction of multipath time delay in frequency domain to UWB chirp signal[J]. Communications Technology, 2010, 43(12):15-17. | |
| 11 | Yu Ge, Sheng-chun Piao, Han Xiao. Fractional fourier transform-based detection and delay time estimation of moving target in strong reverberation environment[J]. IET Radar Sonar & Navigation, 2017, 11(9): 1367-1372 . |
| 12 | 曲杨, 王春晖, 高洁, 等. 基于连续线性调频激光器的测距方法[J]. 红外与激光工程, 2015, 44(6): 1779-1783. |
| Qu Yang, Wang Chun-hui, Gao Jie, et al. Ranging measurement based on linear frequency modulated continuous laser[J]. Infrared and Laser Engineering, 2015, 44(6): 1779-1783. | |
| 13 | 漆翔宇, 刘会杰, 马天鸣. 基于Morlet小波的LFM雷达信号到达时间估计[J]. 电子设计工程, 2017, 25(24): 59-64. |
| Qi Xiang-yu, Liu Hui-jie, Ma Tian-ming. Arrival time estimation of LFM radar signals based on Morlet wavelets transform[J]. Electronic Design Engineering, 2017, 25(24): 59-64. | |
| 14 | Ren Jia-qi, Dai Xu-chu, Li Hui. Repeater jamming suppression technology based on HHT[C]∥IEEE Radar Conference,Philadelphia, USA, 2016. |
| 15 | Stockwell R G, Mansinha L, Lowe R P. Localization of the complex spectrum: the S transform[J]. IEEE Transactions on Signal Processing, 1996, 44(4): 998-1001. |
| 16 | Xin Yu, Hao Hong, Li Jun. Time-varying system identification by enhanced empirical wavelet transform based on synchroextracting transform[J]. Engineering Structures, 2019, 196: No. 10931313. |
| 17 | Lim S, Lee S. Hough transform based ego-velocity estimation in automotive radar system[J]. Electronics Letters, 2021, 57(2): 80-82. |
| 18 | Yu Gang, Yu Ming-jin, Xu Chuan-yan. Synchroextracting transform[J]. IEEE Transactions on Industrial Electronics, 2017, 64(10): 8042-8054. |
| 19 | Baraniuk R G, Flandrin P, Janssen A J E M, et al. Measuring time-frequency information content using the Rényi entropies[J]. IEEE Transaction on Information Theory, 2001, 47(4): 1391-1409. |
| 20 | Wang Hong-wei, Fan Xiang-yu, Chen You, et al. Recognition method of LFM signals based GSTH transform[J]. Systems Engineering and Electronics, 2016, 38(10): 2228-2234. |
| 21 | Niu Meng, Liu Guang-bin. Multi component LFM signal time frequency detection based on S-hough transform[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2007, 27(3): 266-268. |
| 22 | Zhang Wei-ke, Cui Kai-bo, Wu Wei-wei, et al. DOA estimation of LFM signal based on single-source time-frequency points selection algorithm by using the Hough transform[J]. Radio Engineering, 2019, 27(1): 265-275. |
| 23 | Xu Fen-fei, Bao Qing-long, Chen Zeng-ping, et al. Parameter Estimation of multi-component lfm signals based on STFT+Hough transform and fractional Fourier transform[C]∥The 2nd IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xi'an, China, 2018. |
| 24 | Yuan Ye, Mei Wen-bo. Chirp-Like Jammer excision in DSSS communication systems using combined hht spectrum and Hough transform[C]∥The 4th IEEE International Conference on Circuits and Systems for Communications, Shanghai, China, 2008. |
| 25 | Dong Yong-kang, Zhu Zong-da, Tian Xiao-ning, et al. Frequency-modulated continuous-wave LIDAR and 3D imaging by using linear frequency modulation based on injection locking[J]. Journal of Lightwave Technology, 2021, 39(8): 2275-2280. |
| [1] | 窦慧晶,丁钢,高佳,梁霄. 基于压缩感知理论的宽带信号波达方向估计[J]. 吉林大学学报(工学版), 2021, 51(6): 2237-2245. |
| [2] | 金心宇,谢慕寒,孙斌. 基于半张量积压缩感知的粮情信息采集[J]. 吉林大学学报(工学版), 2021, 51(1): 379-385. |
| [3] | 郭立民,陈鑫,陈涛. 基于AlexNet模型的雷达信号调制类型识别[J]. 吉林大学学报(工学版), 2019, 49(3): 1000-1008. |
| [4] | 路伟涛, 杨文革, 洪家财. 改进的小波空域相关滤波算法[J]. 吉林大学学报(工学版), 2015, 45(3): 1005-1011. |
| [5] | 杨巍,石要武. 基于分数阶傅里叶变换的宽带Chirp信号的波达方向角估计[J]. 吉林大学学报(工学版), 2014, 44(3): 818-821. |
| [6] | 李靖, 王树勋, 汪飞. 基于多项式变换的自适应Chirp信号参数估计[J]. 吉林大学学报(工学版), 2004, (4): 617-621. |
|
||