大跨度拱桥拱肋偏心距增大系数计算方法

doi:10.13229/j.cnki.jdxbgxb20220147

吉林大学学报(工学版) ›› 2022, Vol. 52 ›› Issue (6): 1404-1412.doi: 10.13229/j.cnki.jdxbgxb20220147

• 交通运输工程·土木工程 • 上一篇

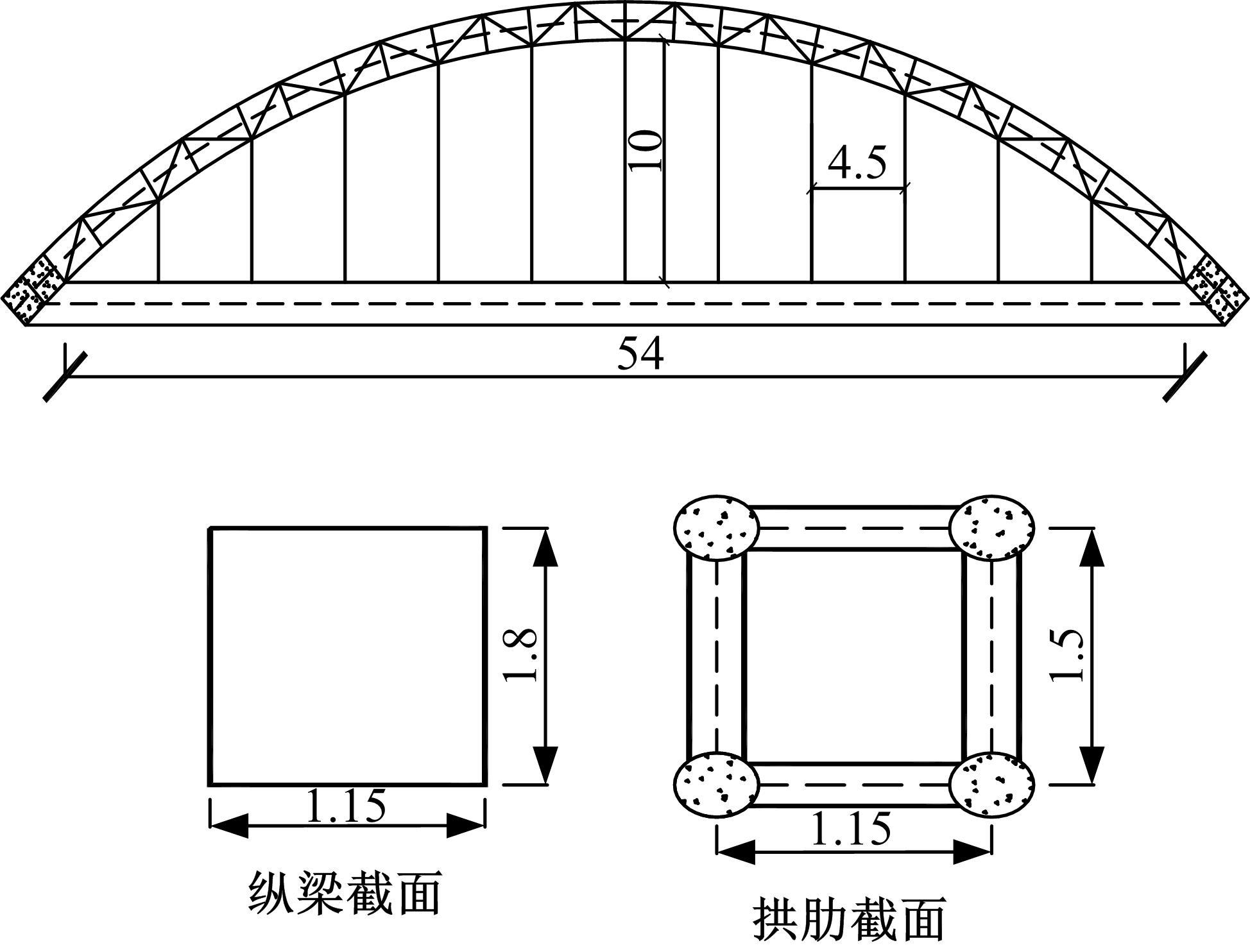
大跨度拱桥拱肋偏心距增大系数计算方法

郭峰^1,²(),李鹏飞³(),毛佳艳⁴,董延昭⁴

^1.石家庄铁道大学土木工程学院，石家庄 050043
^2.石家庄铁道大学道路与铁道工程安全保障省部共建教育部重点实验室，石家庄 050043
^3.旧桥检测与加固技术交通行业重点实验室（北京），北京 100085
^4.石家庄市轨道交通集团有限责任公司，石家庄 050035

收稿日期:2022-01-30 出版日期:2022-06-01 发布日期:2022-06-02
通讯作者: 李鹏飞 E-mail:guofeng2013@126.com;pf.li@rioh.cn
作者简介:郭峰（1983-），男，讲师，博士. 研究方向：桥梁与结构工程. E-mail：guofeng2013@126.com
基金资助:
河北省科技厅项目(216Z6101G);河北省教育厅项目(QN2020207);旧桥检测与加固技术交通行业重点实验室项目(2020-8204)

Calculation method of eccentricity increase coefficient of arch rib of long⁃span arch bridge

Feng GUO^1,²(),Peng-fei LI³(),Jia-yan MAO⁴,Yan-zhao DONG⁴

^1.School of Civil Engineering，Shijiazhuang Tiedao University，Shijiazhuang 050043，China
^2.Key Laboratory of Roads and Railway Engineering Safety Control，Ministry of Education，Shijiazhuang Tiedao University，Shijiazhuang 050043，China
^3.Key Laboratory of Transportation Industry of Old Bridge Inspection and Reinforcement Technology （Beijing），Beijing 100085，China
^4.Shijiazhuang Rail Transportation Group Co. ，Ltd. ，Shijiazhuang 050035，China

Received:2022-01-30 Online:2022-06-01 Published:2022-06-02
Contact: Peng-fei LI E-mail:guofeng2013@126.com;pf.li@rioh.cn

摘要/Abstract

摘要：

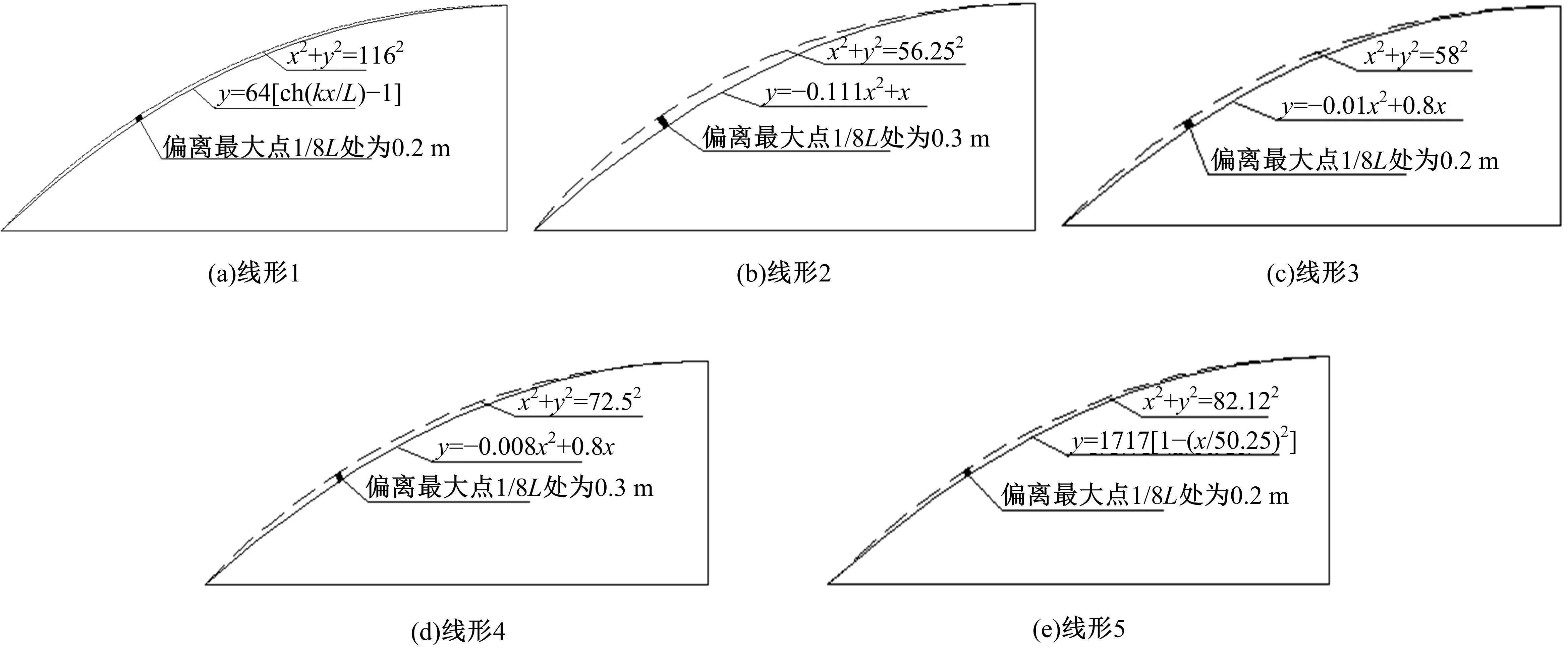
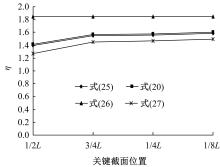
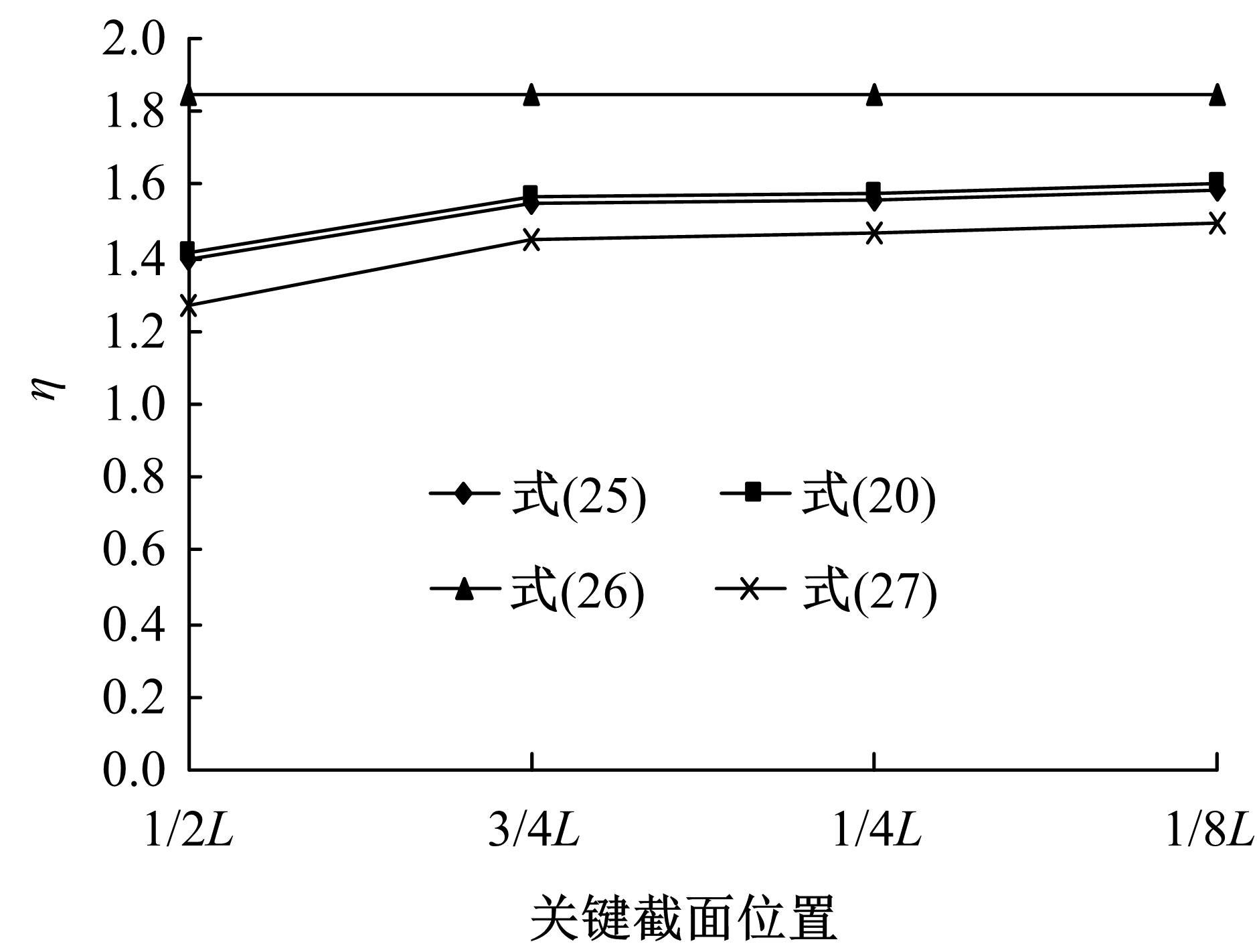
结合变分法基本原理和系杆拱结构变形后相互作用的特点，提出了实用的偏心距增大系数计算方法。通过工程案例分析，将本文计算方法与桥梁规范方法、有限元方法的计算结果进行对比，结果表明：规范方法的计算结果最大，本文方法的计算结果较大，有限元方法的计算结果偏小，本文方法的适用范围较广且具有安全性；悬链线、抛物线、圆弧线和两端带约束的直杆的偏心距增大系数计算有较大区别，与系杆拱的约束条件及荷载形式有关。

关键词: 变分法, 弯矩增大系数, 应变势能, 二阶弯矩效应, 拱肋

Abstract:

Combined with the basic principle of variational method and the characteristics of interaction after deformation of tied arch structure， a practical calculation method of eccentric distance increase coefficient is proposed. Through engineering case analysis， the calculation result of this paper is compared with the normative method of bridge and the finite element method. The results show that the calculation formula specified in the code has the largest result， the calculation result of the formula is large， the finite element calculation result is small. This above means the proposed method is widely applicable and safe. The calculations of the eccentricity increase coefficient of are quite different in catenary， parabola， circular arc and straight rod with constraints at both ends， related to the constraint conditions of the tie-rod arch and the forms of load.

Key words: variational method, moment amplification coefficient, strain potential energy, second-order moment effect, arch rib

中图分类号:

TU318

郭峰,李鹏飞,毛佳艳,董延昭. 大跨度拱桥拱肋偏心距增大系数计算方法[J]. 吉林大学学报(工学版), 2022, 52(6): 1404-1412.

Feng GUO,Peng-fei LI,Jia-yan MAO,Yan-zhao DONG. Calculation method of eccentricity increase coefficient of arch rib of long⁃span arch bridge[J]. Journal of Jilin University(Engineering and Technology Edition), 2022, 52(6): 1404-1412.

图/表 12

图1

表1

图2

图3

图4

图5

图6

图7

表2

表3

表4

本文偏心距增大系数与其他算法对比"

关键截面位置	$η 1 - η 2 η 2 / %$	$η 1 - η 3 η 3 / %$	$η 1 - η 4 η 4 / %$
L/2	0.71	24.66	10.35
L/4	1.32	15.94	9.24

表4

图8

参考文献 13

1	黄侨, 黄义理, 郑清刚, 等. 常泰长江大桥塔柱偏心距增大系数的计算方法[J].长安大学学报: 自然科学版, 2021, 41(3): 42-51.
	Huang Qiao, Huang Yi-li, Zheng Qing-gang, et al. Calculation methods of pylon eccentricity magnified coefficient of Changtai Yangtze River Bridge[J]. Journal of Chang'an University(Natural Science Edition), 2021, 41(3): 42-51.
2	李春阳. 复杂边界下柔性高墩的受力性能研究[D]. 长沙:湖南大学土木工程学院, 2018.
	Li Chun-yang. The research on mechanical behavior of flexible high-piers with complex boundary conditions[D]. Changsha: School of Civil Engineering, Hunan University, 2018.
3	. 公路钢筋混凝土及预应力混凝土桥涵设计规范 [S].
4	Wang Qiu-wei, Shi Qing-xuan, Jiang Wei-shan. The second-order effect of src columns under eccentric compression[J]. Mechanics in Engineering, 2011, 33(3): 34-37, 41.
5	王浩然, 许晶. 钢筋混凝土结构的二阶效应分析方法[C]∥北京力学会第二十四届学术年会, 中国, 北京, 2018: 946-948.
	Wang Hao-ran, Xu Jing. Second order effect analysis method of reinforced concrete structures[C]∥Proceedings of the 24th Annual Academic Conference of Beijing Society of Mechanics, Beijing, China, 2018: 946-948.
6	苑仁安, 傅战工, 郑清刚, 等. 超高桥塔结构偏心距增大系数计算方法[J]. 桥梁建设, 2021, 51(5): 37-43.
	Yuan Ren-an, Fu Zhan-gong, Zheng Qing-gang, et al. Calculation method of eccentricity increasing coefficient of super high bridge tower structure[J]. Bridge Construction, 2021, 51 (5): 37-43.
7	李志渊, 陈全红. 钢筋砼长柱偏心距增大系数计算方法比较[J]. 兰州交通大学学报:自然科学版, 2007, 26(4): 66-69.
	Li Zhi-yuan, Chen Quan-hong. Comparative study on the calculation method for eccentricity accreting factor of reinforced concrete slender columns[J] Journal of Lanzhou Jiaotong University(Natural Science), 2007, 26(4): 66-69.
8	徐田. FRP约束钢筋混凝土柱的承载性能研究[D]. 哈尔滨:哈尔滨工业大学土木工程学院, 2007.
	Xu Tian. Research on bearing capacity of FRP confined reinforced concrete columns[D]. Harbin: School of Civil Engineering, Harbin Institute of Technology, 2007
9	Yun Y W, Liu X H, Kim S K, et al. Research on eccentricity magnification factor of eccentric compression lightweight aggregate concrete member[J]. Advanced Materials Research, 2011, 152-153: 717-721.
10	Rahman M E, Ting T Z H, Lau H H, et al. Behaviour of lightweight concrete wall panel under axial loading: experimental and numerical investigation toward sustainability in construction industry[J]. Buildings, 2021, 11(12): 620.
11	Robinson G P, Palmeri A, Austin S A. Design methodologies for one way spanning eccentrically loaded minimally or centrally reinforced pre-cast RC panels[J]. Engineering Structures, 2013, 56: 1945-1956.
12	Ting T Z H, Rahman M E, Lau H H, et al. Recent development and perspective of lightweight aggregates based self-compacting concrete[J]. Construction and Building Materials, 2019, 201: 763-777.
13	Ho N M, Doh J H. Prediction of ultimate strength of concrete walls restrained on three sides[J]. Structural Concrete, 2019, 20(3): 942-954.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

桥名	偏离图示	跨径/m	矢跨比	拱肋线形	拱截面高度/m	与圆弧线偏离值/m	弧度长度偏离值/m
拱肋1	I	160	1/5.1	三次抛物线	3.8	0.15	2.01
拱肋2	II	90	1/4.8	悬链线	2.0	0.27	1.90
拱肋3	III	80	1/4.7	悬链线	1.4	0.18	1.11
拱肋4	IV	100	1/5.1	三次抛物线	2.6	0.19	1.21
拱肋5	V	100.5	1/5.75	三次抛物线	2.7	0.21	1.01

关键截面位置	轴向压力值/kN	弹性弯矩值/（kN·m）	几何非线性弯矩值/（kN·m）
1/2L	6501.2	1641.654	1292.598
1/4L	9104.7	1731.450	1210.842

参数	关键截面位置		参数	关键截面位置
参数	L/2	L/4	参数	L/2	L/4
系杆截面刚度/（N·m^-1）	0.57	0.57	K	1.10	1.10
拱肋截面刚度/（N·m^-1）	0.33	0.33	P	0.05	0.05
化解为圆弧后半径R/m	42.28	42.28	η₁	1.43	1.60
拱肋弧线长度S/m	64.35	64.35	η₂	1.44	1.61
截面偏心距e₀/m	0.26	0.20	η₃	1.89	1.89
圆心角值α/（°）	0.22	0.22	η₄	1.30	1.50

大跨度拱桥拱肋偏心距增大系数计算方法

Calculation method of eccentricity increase coefficient of arch rib of long⁃span arch bridge

RICH HTML

PDF (PC)

摘要/Abstract

引用本文

使用本文

图/表 12

参考文献 13

相关文章 1

Metrics

本文评价

推荐阅读 0