弹簧连接质量块压电悬臂梁低频和超宽频性能优化

doi:10.13229/j.cnki.jdxbgxb.20211323

摘要/Abstract

摘要：

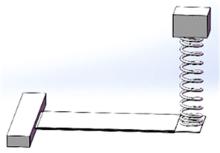
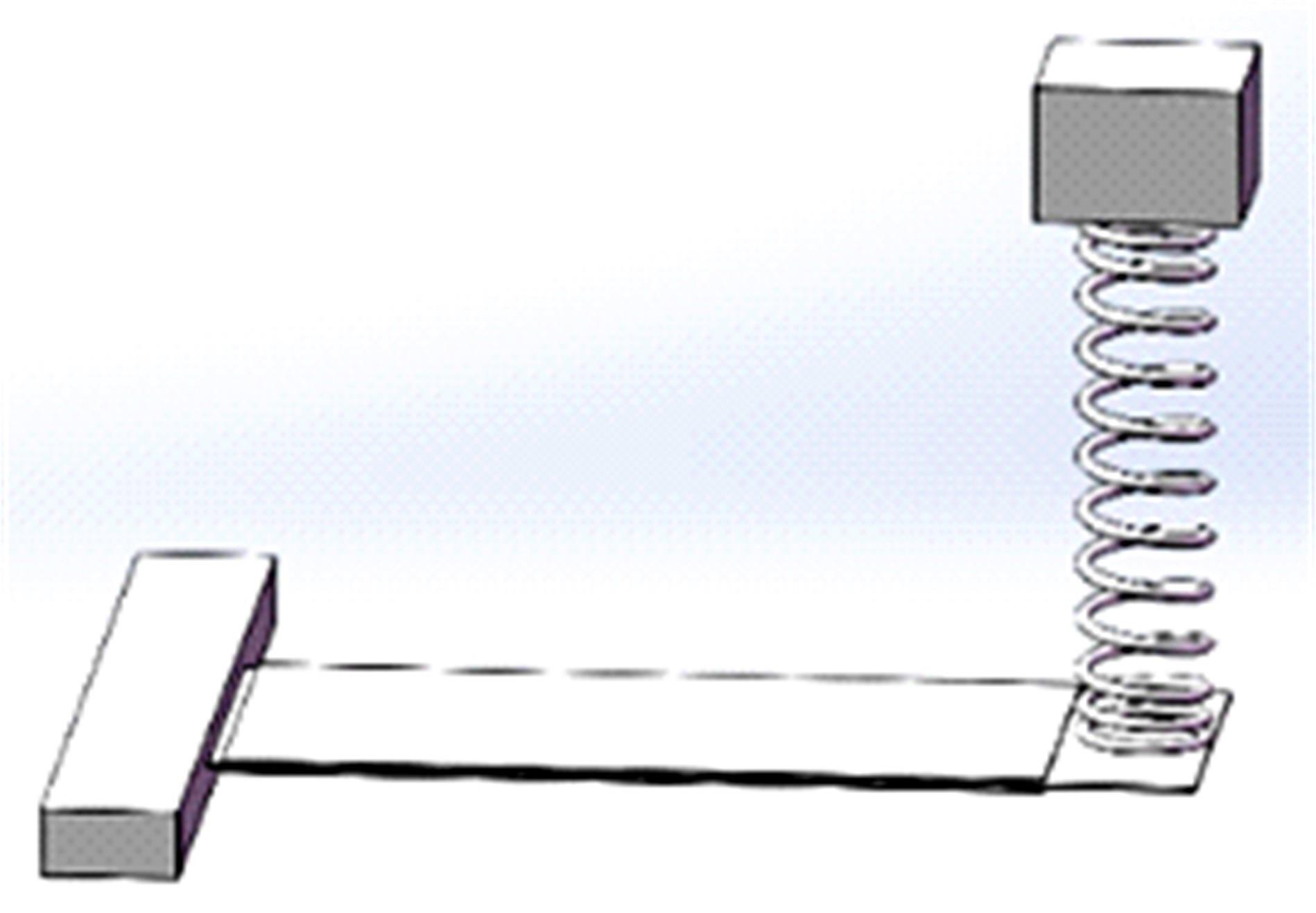
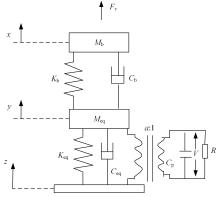
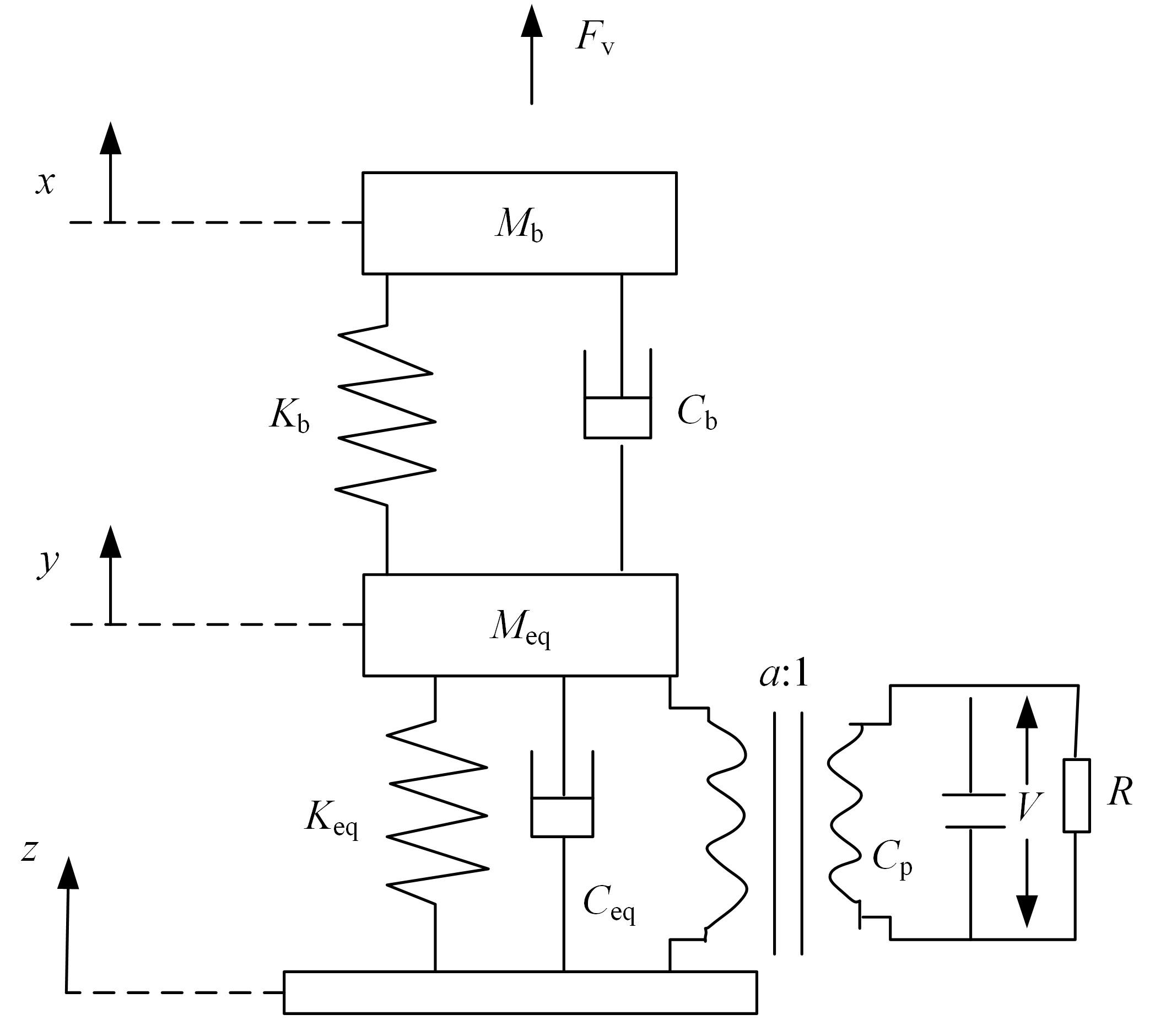
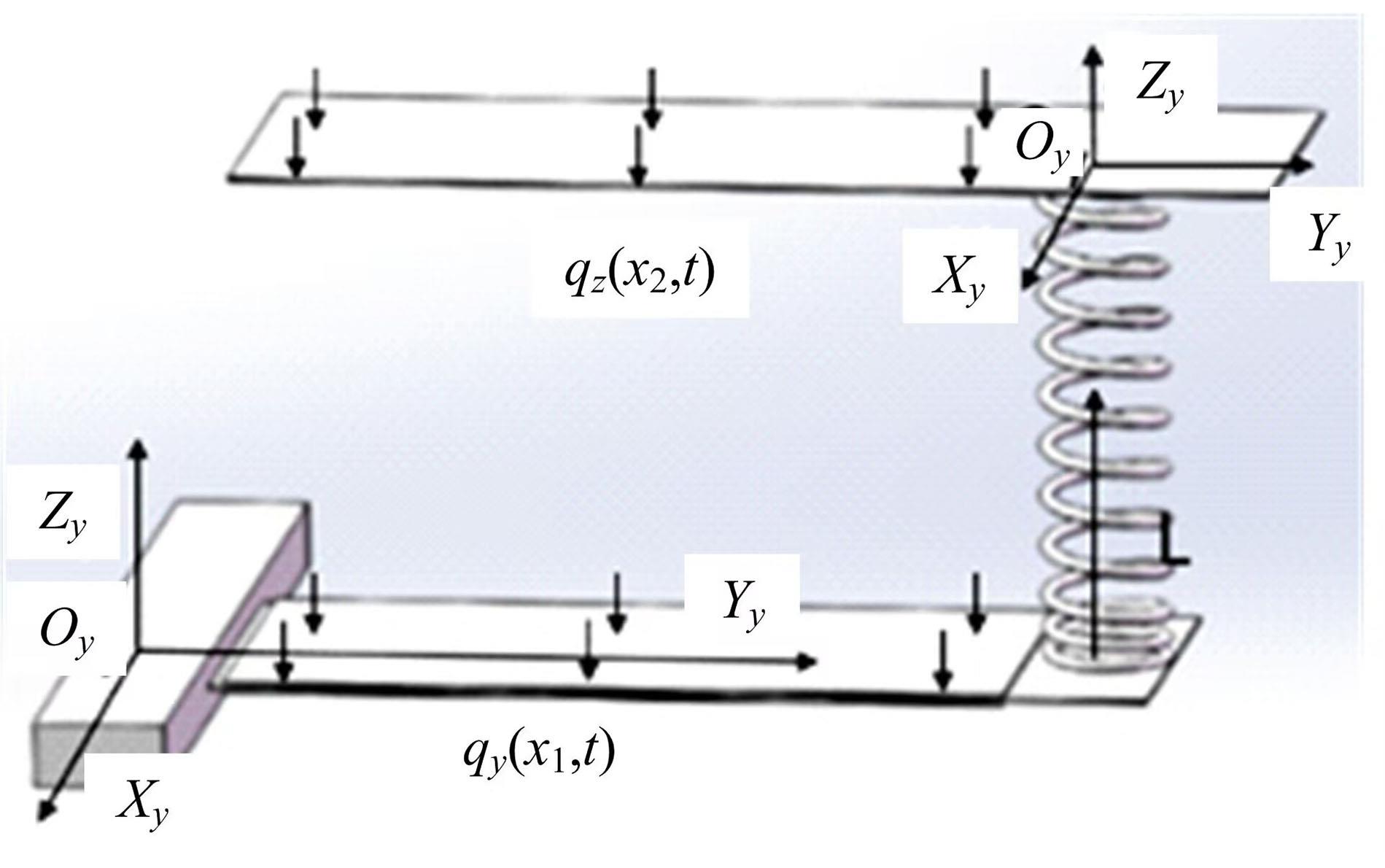
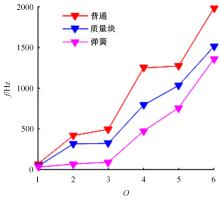
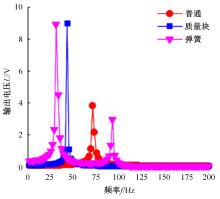
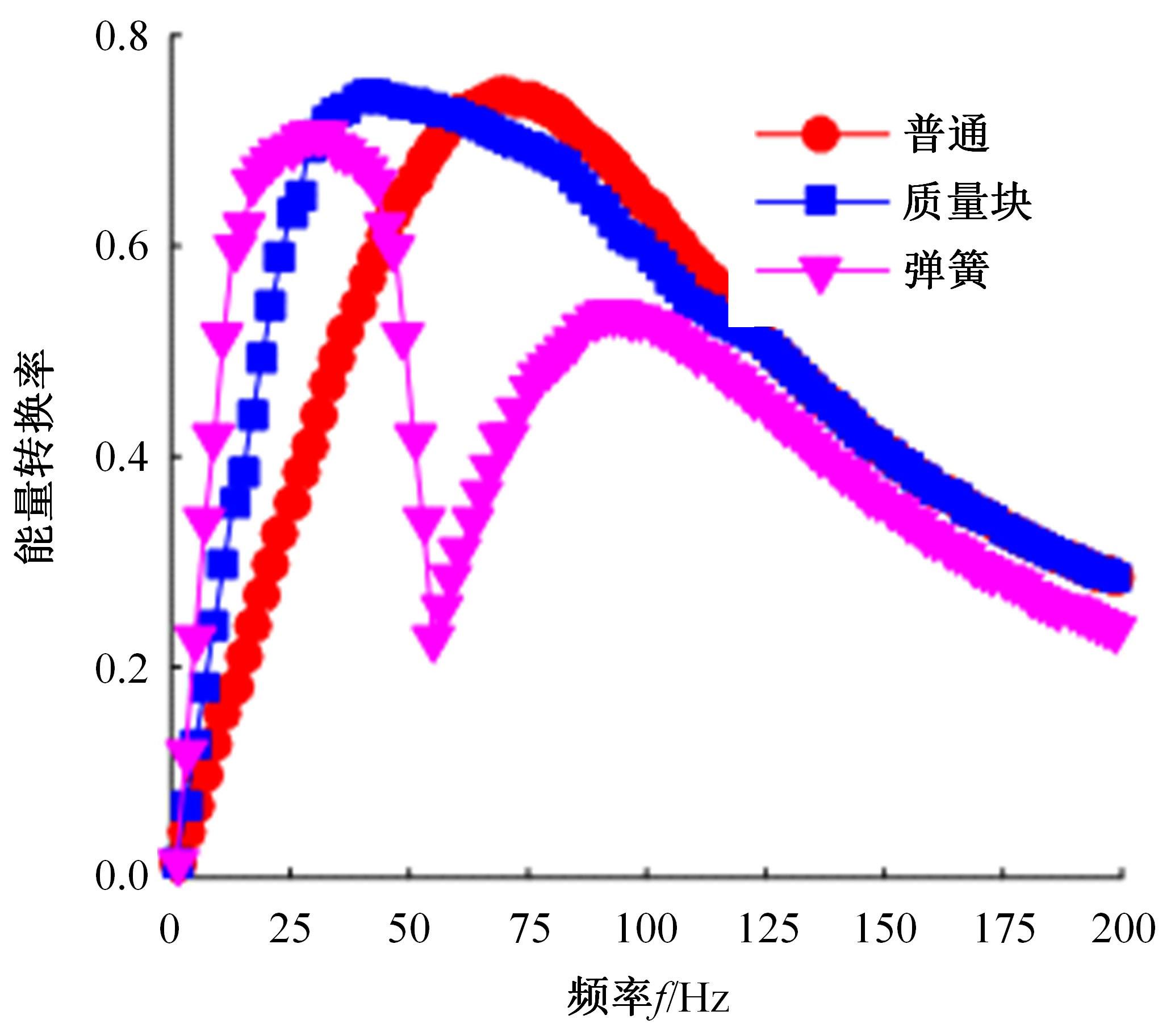
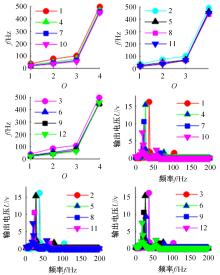
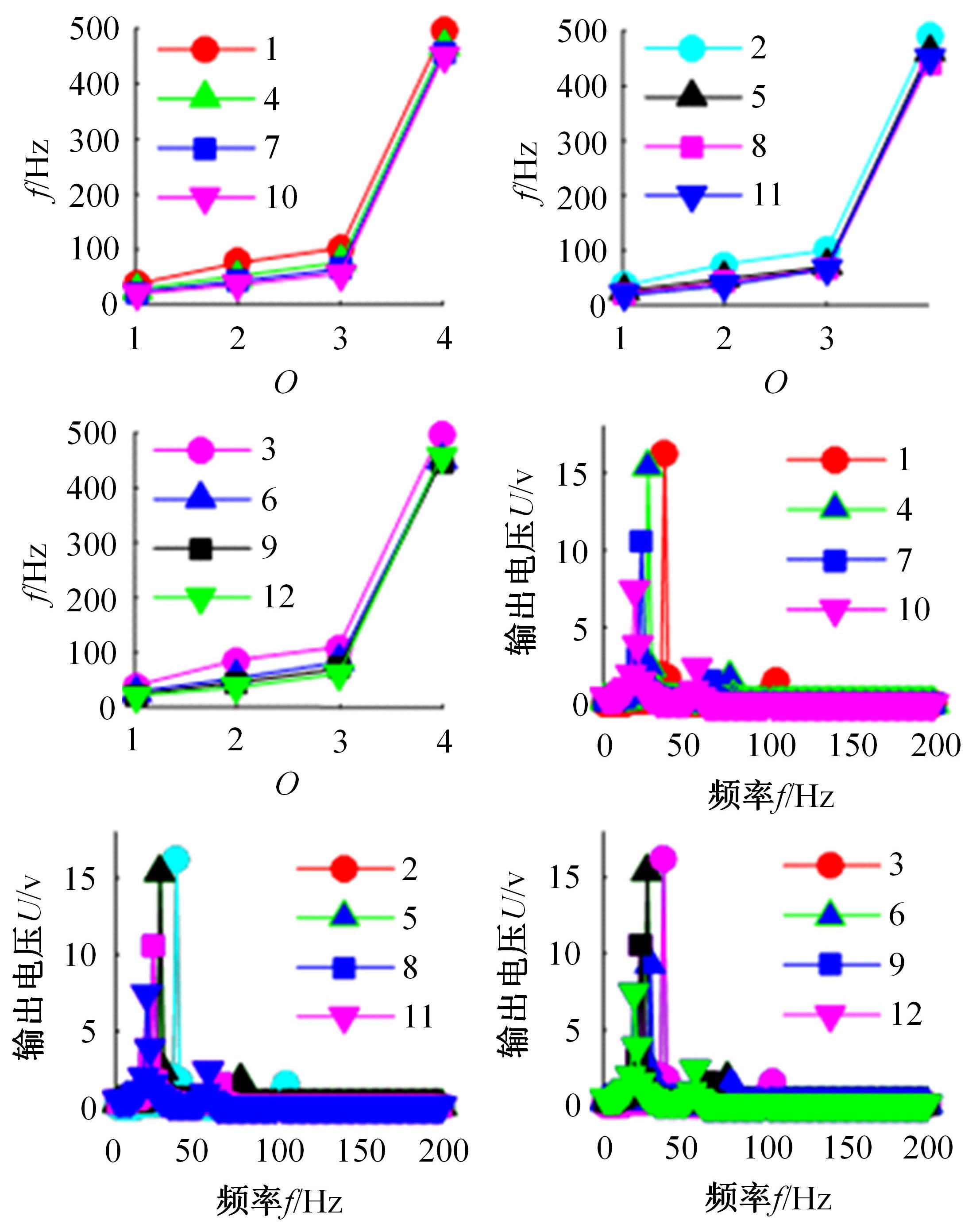
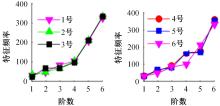
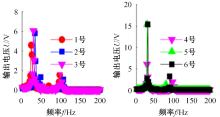
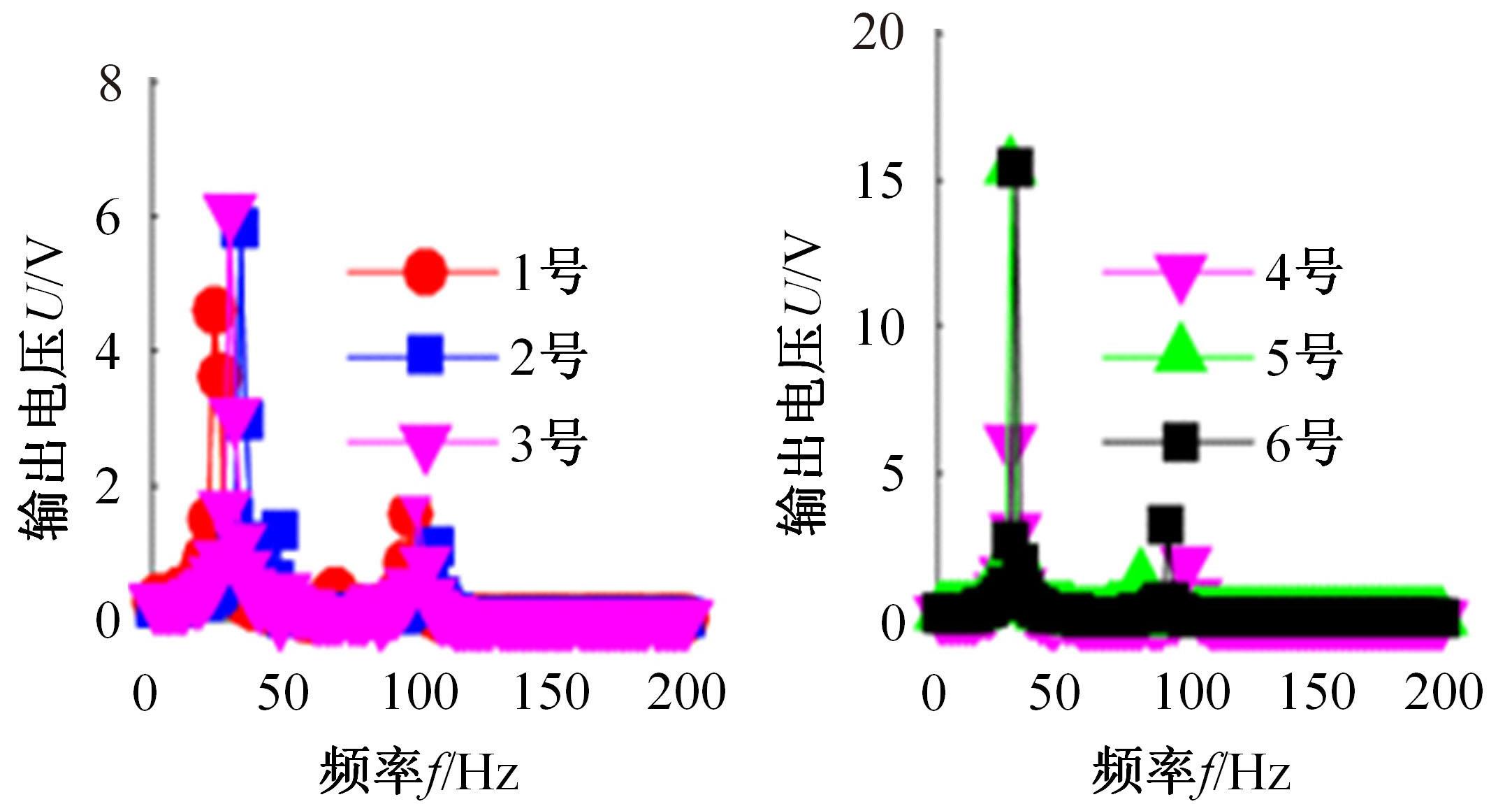
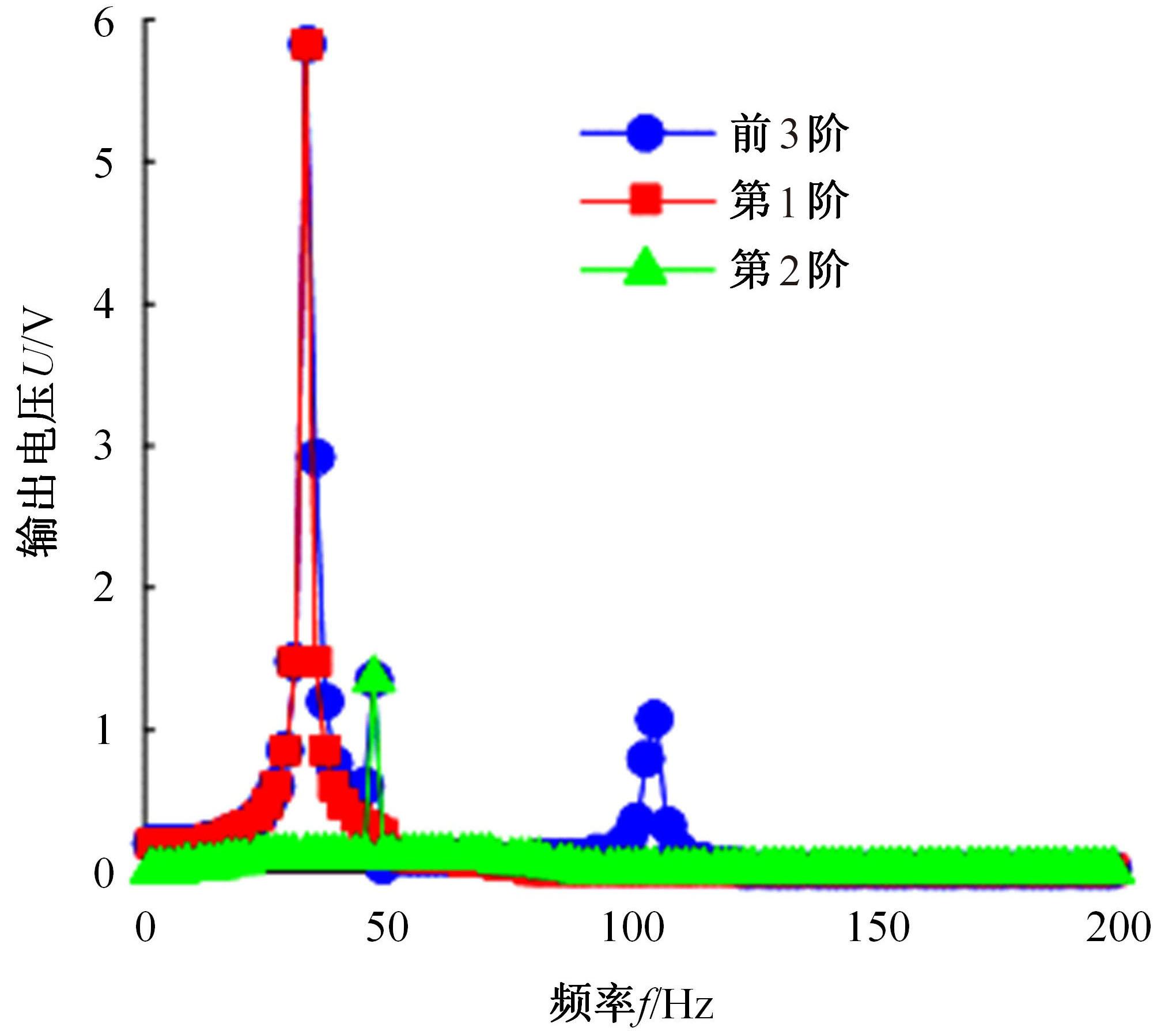
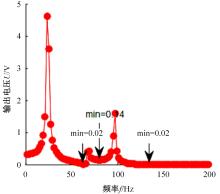
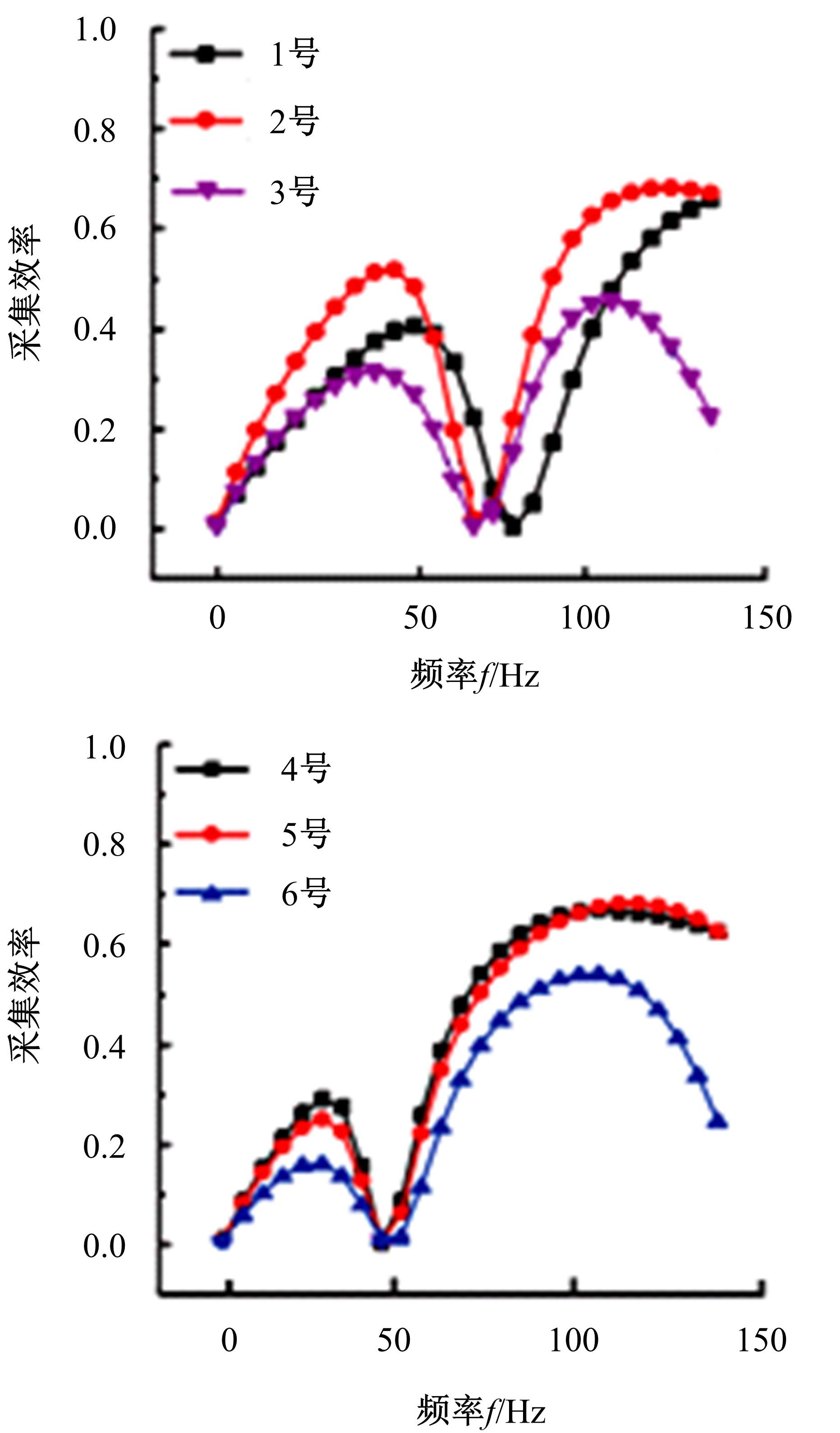
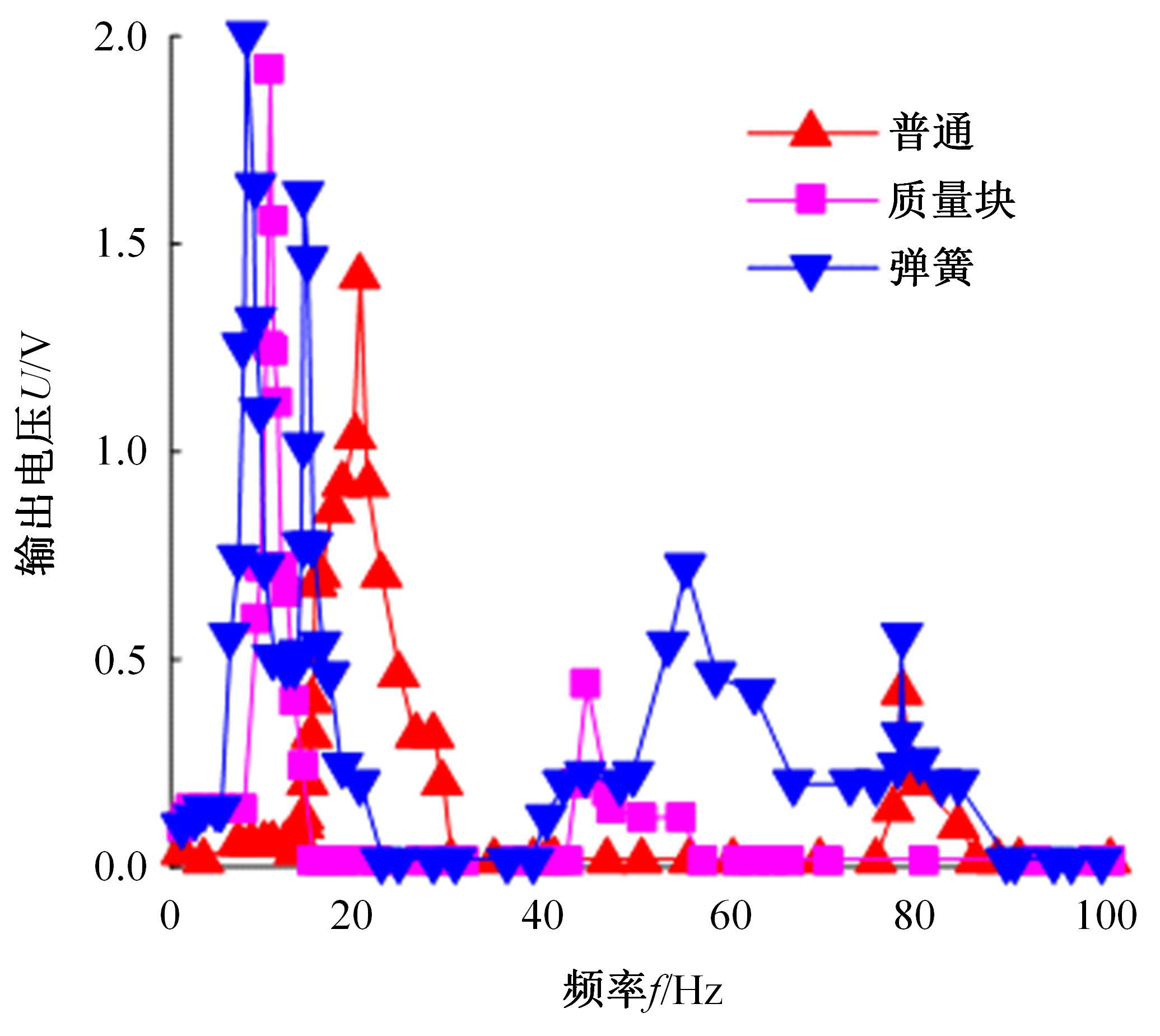
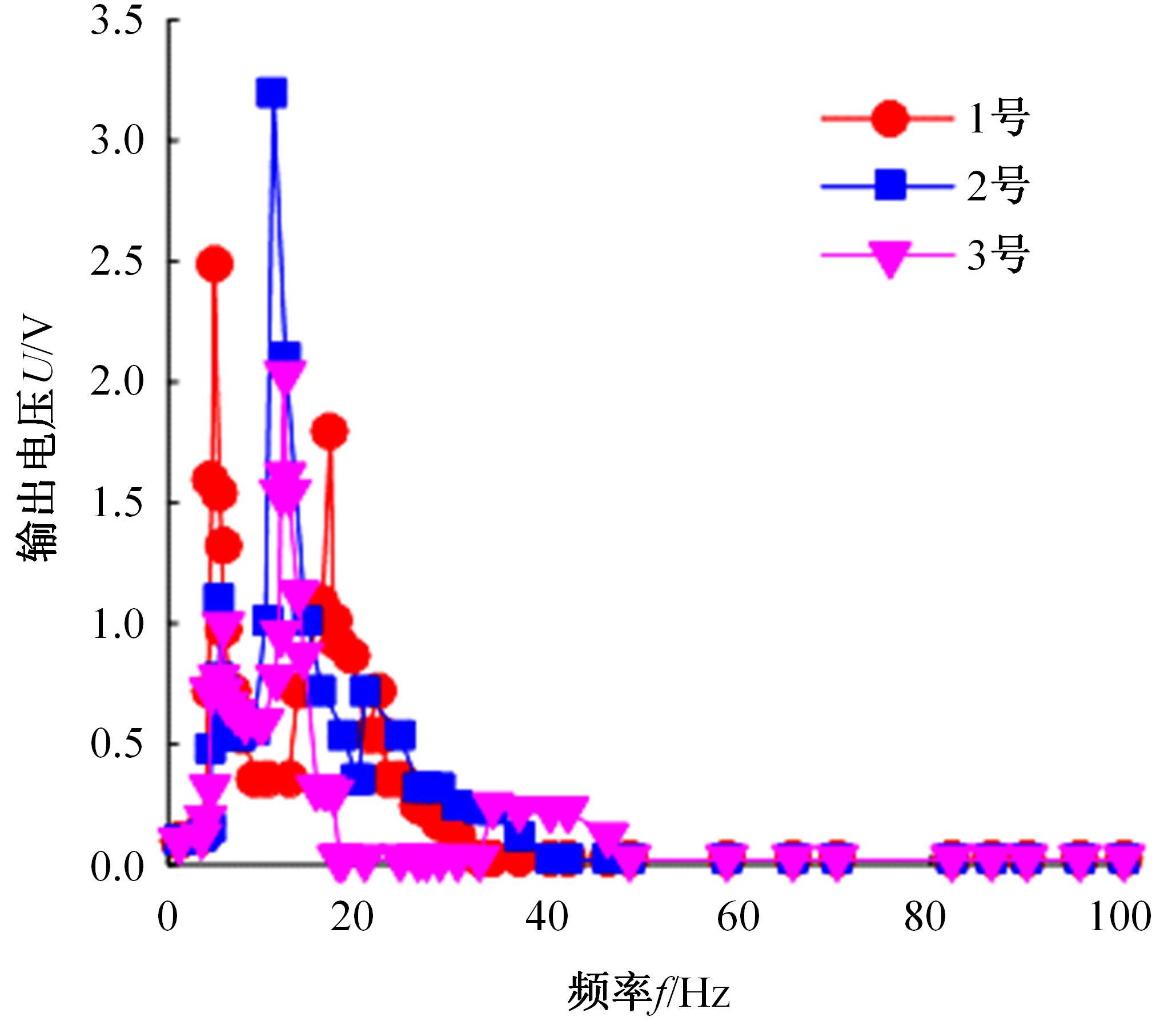
针对压电悬臂梁因固有频率过高、频带窄等原因导致的振动能量采集效率低、实际应用效果不佳的问题，通过欧拉-伯努利梁的特征频率方程，分析悬臂梁收集能量的特性和振动学特性，得到影响压电悬臂梁固有频率的3个参数：有效刚度、有效质量和自由端惯性矩。提出一种通过改变整体有效刚度来优化悬臂梁的弹簧连接质量块式结构，并进一步通过改变结构的惯性矩得出多自由度弹簧悬臂梁，降低了梁的固有频率，并在仿真实验中得到验证。仿真实验中发现由于两阶谐振频率间距减小而产生频带叠加的现象，通过两阶频带分解解释其产生的可能性。实验结果得出弹簧连接质量块式悬臂梁结构较传统而言，输出电压提高30%，频带拓宽为原来的2.5倍；虽然与质量块悬臂梁相比改善效果不明显，但引入多自由度后输出电压最高能提高60%，频带拓宽最高为质量块悬臂梁的3.3倍。

关键词: 压电悬臂梁, 固有频率, 弹簧连接质量块, 多自由度, 频带叠加

Abstract:

Aiming at the problems of low vibration energy collection efficiency and poor practical application effect caused by high natural frequency and narrow frequency band of piezoelectric cantilever beam， the characteristics of energy collection and vibration characteristics of cantilever beam were analyzed by the characteristic frequency equation of Euler-Bernoulli beam， and three parameters affecting the natural frequency of piezoelectric cantilever beam were obtained ： effective stiffness， effective mass and free end inertia moment. A spring-connected mass block structure was proposed to optimize the cantilever beam by changing the overall effective stiffness， and the multi-degree-of-freedom spring cantilever beam was obtained by changing the inertia moment of the structure， which reduced the natural frequency of the beam and was verified in the simulation experiment. In the simulation experiment， it was found that the frequency band superposition phenomenon occured？ due to the decrease of the two-order resonant frequency spacing， and the possibility of its generation was explained by the two-order frequency band decomposition. The experimental results showed that the output voltage of the spring-connected mass block cantilever beam structure was increased by 30% and the frequency band was widened by 2.5 times compared with the traditional structure. Although the improvement effect was not obvious compared with the mass cantilever beam， the output voltage can be increased by 60% and the frequency band width can be increased by 3.3 times after the introduction of multi-degree of freedom.

Key words: piezoelectric cantilever beam, natural frequency, spring-connected mass, multiple degrees of freedom, frequency band superposition

中图分类号:

TN712

蒋建东,叶桢,乔欣. 弹簧连接质量块压电悬臂梁低频和超宽频性能优化[J]. 吉林大学学报(工学版), 2023, 53(10): 2807-2816.

Jian-dong JIANG,Zhen YE,Xin QIAO. Low and ultra-wideband performance optimization of spring-connected mass piezoelectric cantilever[J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(10): 2807-2816.

图/表 21

图1

图2

图3

图4

表1

压电振子材料参数设置"

材料	$ρ / (k g · m - 3)$	$μ$	$E / G P a$	尺寸A×B×C/ （mm×mm×mm）
PZT-5H	7500	0.31	71	60×30×0.2
铍青铜	8300	0.35	130	70×30×0.2
ABS	1200	0.39	2	10×80×5
弹簧（1360）	8000	0.50	150	10×40×1
质量块1	2500	0.35	130	15×15×10
质量块2	2500	0.35	130	15×15×8.5
质量块3	7800	0.35	130	60×30×0.4

表1

图5

图6

图7

表2

图8

图9

图10

图11

图12

图13

图14

图15

图16

图17

图18

图19

参考文献 21

1	钱志鸿,王义君. 面向物联网的无线传感器网络综述[J]. 电子与信息学报,2013,35(1): 215-227.
	Qian Zhi-hong, Wang Yi-jun. Internet of things-oriented wireless sensor networks review[J]. Journal of Electronics & Information Technology, 2013, 35(1): 215-227.
2	Mazumdar N, Nag A. Cache-aware mobile data collection schedule for IOT enabled multi-rate data generator wireless sensor network[J]. Sustainable Computing: Informatics and Systems, 2021(31):No. 100583.
3	Worlu C, Jamal A A, Mahiddin N A. Wireless sensor networks, internet of things, and their challenges[J]. International Journal of Innovative Technology and Exploring Engineering, 2019, 8(12): 556-566.
4	Safaei M, Sodano H A, Anton S R. A review of energy harvesting using piezoelectric materials: state-of-the-art a decade later (2008–2018)[J]. Smart Materials and Structures, 2019, 28(11): No.113001.
5	徐振龙,单小彪,谢涛,等. 宽频压电振动俘能器的研究现状综述[J]. 振动与冲击,2018,7(8): 190-199, 205.
	Xu Zhen-long, Shan Xiao-biao, Xie Tao, et al. A review of broadband piezoelectric vibration energy harvester[J]. Journal of Viration and Shock, 2018, 37(8): 190-199, 205.
6	Shen D, Park J H, Ajitsaria J, et al. The design, fabrication and evaluation of a MEMS PZT cantilever with an integrated Si proof mass for vibration energy harvesting[J]. Journal of Micromechanics and Microengineering, 2008, 18(5): No.055017.
7	Li W G, He S, Yu S. Improving power density of a cantilever piezoelectric power harvester through a curved L-shaped proof mass[J]. IEEE Transactions on Industrial Electronics, 2009, 57(3): 868-876.
8	Challa V R, Prasad M G, Shi Y, et al. A vibration energy harvesting device with bidirectional resonance frequency tunability[J]. Smart Materials and Structures, 2008, 17(1): No.015035.
9	Liu J Q, Fang H B, Xu Z Y, et al. A MEMS-based piezoelectric power generator array for vibration energy harvesting[J]. Microelectronics Journal, 2008, 39(5): 802-806.
10	Cao D X, Leadenham S, Erturk A. Internal resonance for nonlinear vibration energy harvesting[J]. The European Physical Journal Special Topics, 2015, 224(14): 2867-2880.
11	Chen L Q, Jiang W A, Panyam M, et al. A broadband internally resonant vibratory energy harvester[J]. Journal of Vibration and Acoustics, 2016, 138(6):No.061007.
12	Roundy S, Leland E S, Baker J, et al. Improving power output for vibration-based energy scavengers[J]. IEEE Pervasive Computing, 2005, 4(1): 28-36.
13	Erturk A, Inman D J.压电能量采集(Piezoelectric energy harvesting) [M]. 北京: 国防工业出版社, 2015.
14	蒋建东,张玖利,牛瑞征,等. 耦合弯曲-剪切载荷L型压电振子的低宽频特性[J]. 浙江大学学报:工学版,2021 55(1): 162-168.
	Jian-dong Jang, Zhang Jiu-li, Niu Rui-zheng, et al. Low broadband characteristics of L-shaped piezoelectric cantilever beam with bending shear load[J]. Journal of Zhejiang University (Engineering Science), 2021, 55(1): 162-168.
15	杨斌强,徐文潭,陆国丽,等. 宽频压电振动能量采集器的分布参数模型与实验[J]. 中国机械工程,2017,28(2): 127-134.
	Yang Bin-qiang, Xu Wen-tan, Lu Guo-li, et al. Distributed parameter model and experiments of a broadband piezoelectric vibration energy harvester[J]. Chinese Journal of Mechanical Engineering, 2017, 28(2): 127-134.
16	展永政,王光庆. 压电振动能量采集器的性能分析与功率优化[J]. 浙江大学学报:工学版,2014,48(7): 1248-1253.
	Zhan Yong-zheng, Wang Guang-qing. Performance analysis and power optimization of piezoelectric vibration engineering harvester[J]. Journal of Zhejiang University (Engineering Science), 2014, 48(7): 1248-1253.
17	杨斌强,徐文潭,王学保,等. 带弹性放大器的双稳态压电振动能量采集器[J]. 传感技术学报,2017(30): 684-691.
	Yang Bin-qiang, Xu Wen-tan, Wang Xue-bao, et al. A bistable piezoelectric vibration energy harvester with an elastic magnifier[J]. Chinese Journal of Sensors and Actuators, 2017(30): 684-691.
18	Aldraihem O J, Wetherhold R C, Singh T. Distributed control of laminated beams: Timoshenko theory vs Euler-Bernoulli theory[J]. Journal of Intelligent Material Systems and Structures, 1997, 8(2): 149-157.
19	Liu H, Xu T, Huang Z, et al. Parametric design for a piezoelectric cantilever carrying oscillators to harvest multi-frequency vibration energy[J]. International Journal of Applied Electromagnetics and Mechanics, 2013, 41(4): 389-405.
20	Tang L H, Yang Y W. A nonlinear piezoelectric energy harvester with magnetic oscillator[J]. Applied Physics Letters,2012, 101(9): 094102.
21	夏呈. 修正铁摩辛柯梁受迫振动响应分析及其应用[D]. 南京: 东南大学机械工程学院,2017.
	Xia Cheng. The analysis of forced vibration response of modified Timoshenko beam theory and its application [D]. Nanjing: College of Mechanical Engineering, Southeast University,2017.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

序号	m/g	k	N_f	O₁	V₁	O₂	V₂
1	5	1.36	3	36.8	16.2	75.7	1.60
2	5	3.02	3	37.0	16.1	75.0	1.60
3	5	6.75	3	37.8	15.9	75.4	1.58
4	10	1.36	3	27.2	15.5	51.7	0.24
5	10	3.02	3	27.2	15.4	51.9	0.24
6	10	6.75	3	27.4	9.4	53.2	0.22
7	15	1.36	3	22.6	10.5	41.7	0.26
8	15	3.02	3	22.6	10.7	41.8	0.26
9	15	6.75	3	22.6	10.4	41.8	0.26
10	20	1.36	3	19.7	7.4	36.0	0.31
11	20	3.02	3	19.8	7.4	36.2	0.28
12	20	6.75	3	19.8	7.4	36.6	0.28

[1]	胡明伟,王洪光,潘新安. 基于正交设计的协作机器人全域结构优化设计[J]. 吉林大学学报(工学版), 2021, 51(1): 370-378.
[2]	张天霄, 刘昕晖, 张农. 液压溢流阀的振动分析[J]. 吉林大学学报(工学版), 2014, 44(01): 91-94.
[3]	郭抗, 曾平, 武迪, 程光明. 平板形单振子多自由度压电马达[J]. 吉林大学学报(工学版), 2011, 41(增刊2): 215-220.
[4]	韩志武, 吕尤, 董立春, 张俊秋, 牛士超, 马荣峰, 任露泉. 仿生表面形态齿轮的模态分析[J]. 吉林大学学报(工学版), 2010, 40(06): 1604-1608.
[5]	金文明,李华军,寇淑清,杨慎华. 装配式凸轮轴悬臂式数控装配机的机架模态分析[J]. 吉林大学学报(工学版), 2009, 39(增刊2): 319-0323.
[6]	苏铁坚, 管爱华, 麦莉. 受纵向分布压力的弹性薄板的动力分析[J]. 吉林大学学报(工学版), 2000, (3): 72-74.
[7]	刘寒冰, 龚国庆, 魏媛. 改进的r-收敛和h-收敛自适应有限元方法[J]. 吉林大学学报(工学版), 2000, (3): 56-60.