基于正交设计的协作机器人全域结构优化设计

doi:10.13229/j.cnki.jdxbgxb20190838

吉林大学学报(工学版) ›› 2021, Vol. 51 ›› Issue (1): 370-378.doi: 10.13229/j.cnki.jdxbgxb20190838

• 通信与控制工程 • 上一篇

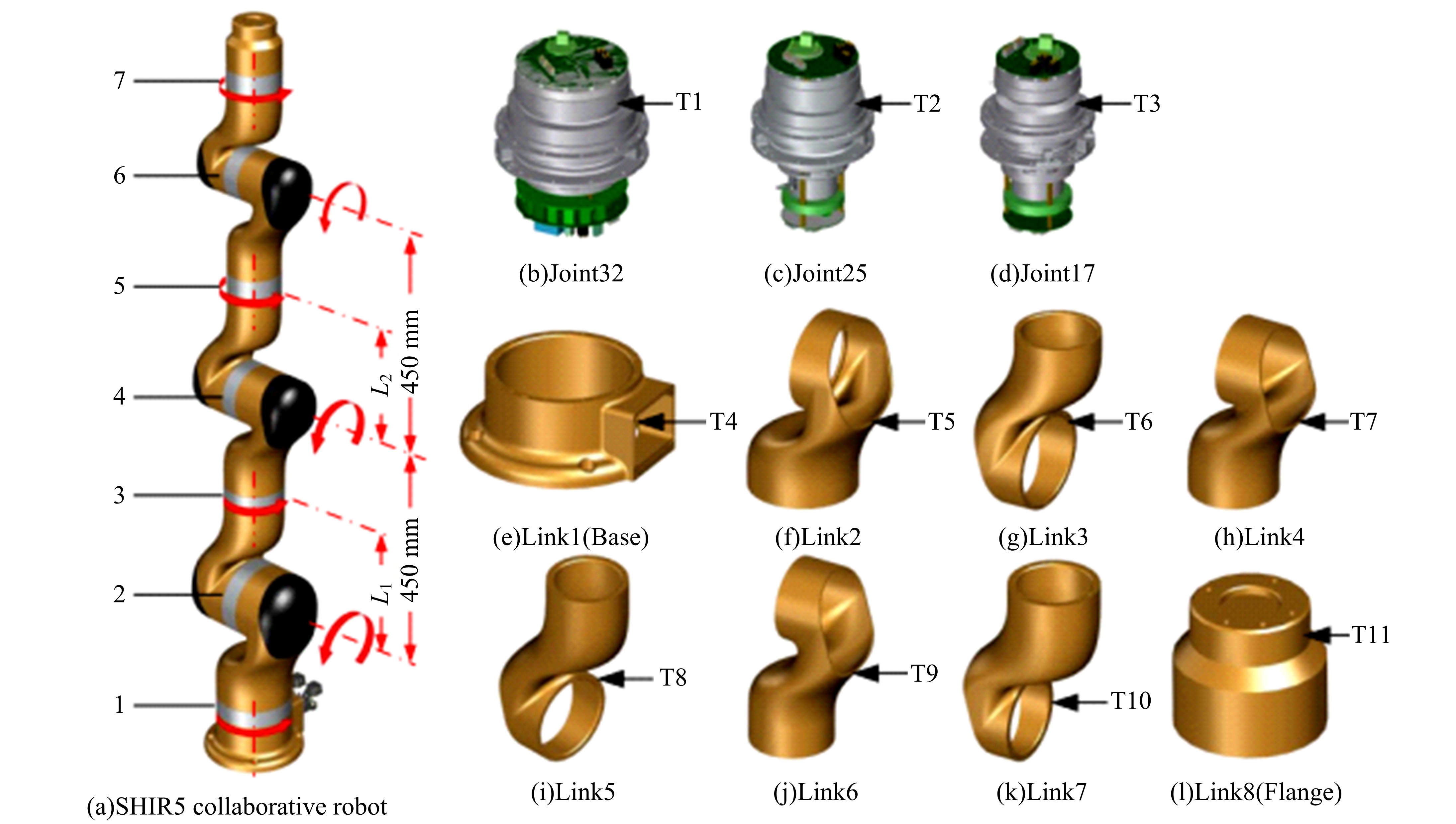
基于正交设计的协作机器人全域结构优化设计

胡明伟^1,^2,³(),王洪光^1,²(),潘新安^1,²

^1.中国科学院沈阳自动化研究所机器人学国家重点实验室，沈阳 110016
^2.中国科学院机器人与智能制造创新研究院，沈阳 110169
^3.中国科学院大学，北京 100049

收稿日期:2019-08-24 出版日期:2021-01-01 发布日期:2021-01-20
通讯作者: 王洪光 E-mail:mingweihu@yeah.net;hgwang@sia.cn
作者简介:胡明伟（1990-），男，博士研究生.研究方向：机械电子. E-mail：mingweihu@yeah.net
基金资助:
国家自然科学基金重点项目(51535008);国家自然科学基金项目(51405482);国家发改委新一代信息基础设施建设工程和“互联网+”重大工程项目(2017-210103-73-03-000009);中国科学院重点部署项目(KGZD-EW-608-1)

Global structural optimization design of collaborative robots using orthogonal design

Ming-wei HU^1,^2,³(),Hong-guang WANG^1,²(),Xin-an PAN^1,²

^1.State Key Laboratory of Robotics，Shenyang Institute of Automation，Chinese Academy of Sciences，Shenyang 110016，China
^2.Institutes for Robotics and Intelligent Manufacturing，Chinese Academy of Sciences，Shenyang 110169，China
^3.University of Chinese Academy of Sciences，Beijing 100049，China

Received:2019-08-24 Online:2021-01-01 Published:2021-01-20
Contact: Hong-guang WANG E-mail:mingweihu@yeah.net;hgwang@sia.cn

摘要/Abstract

摘要：

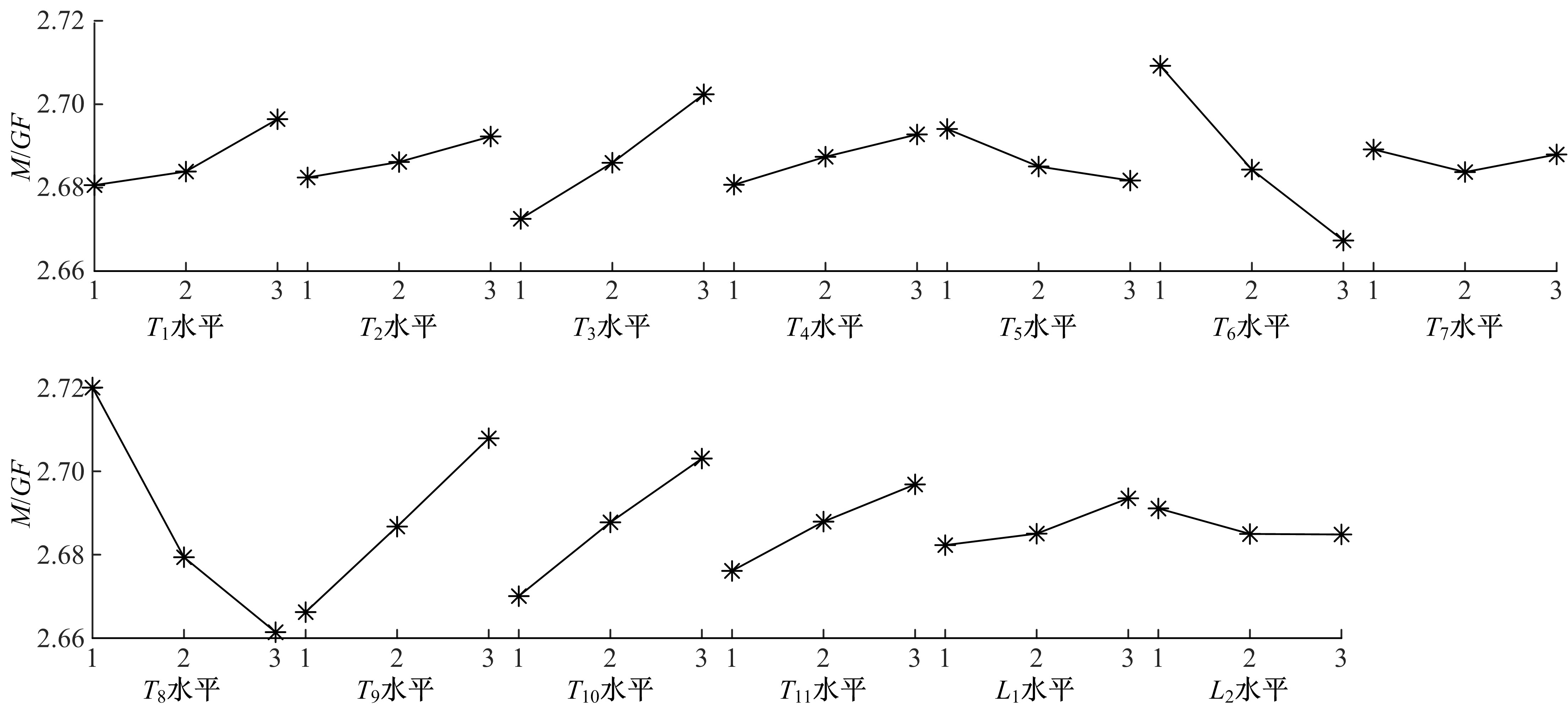
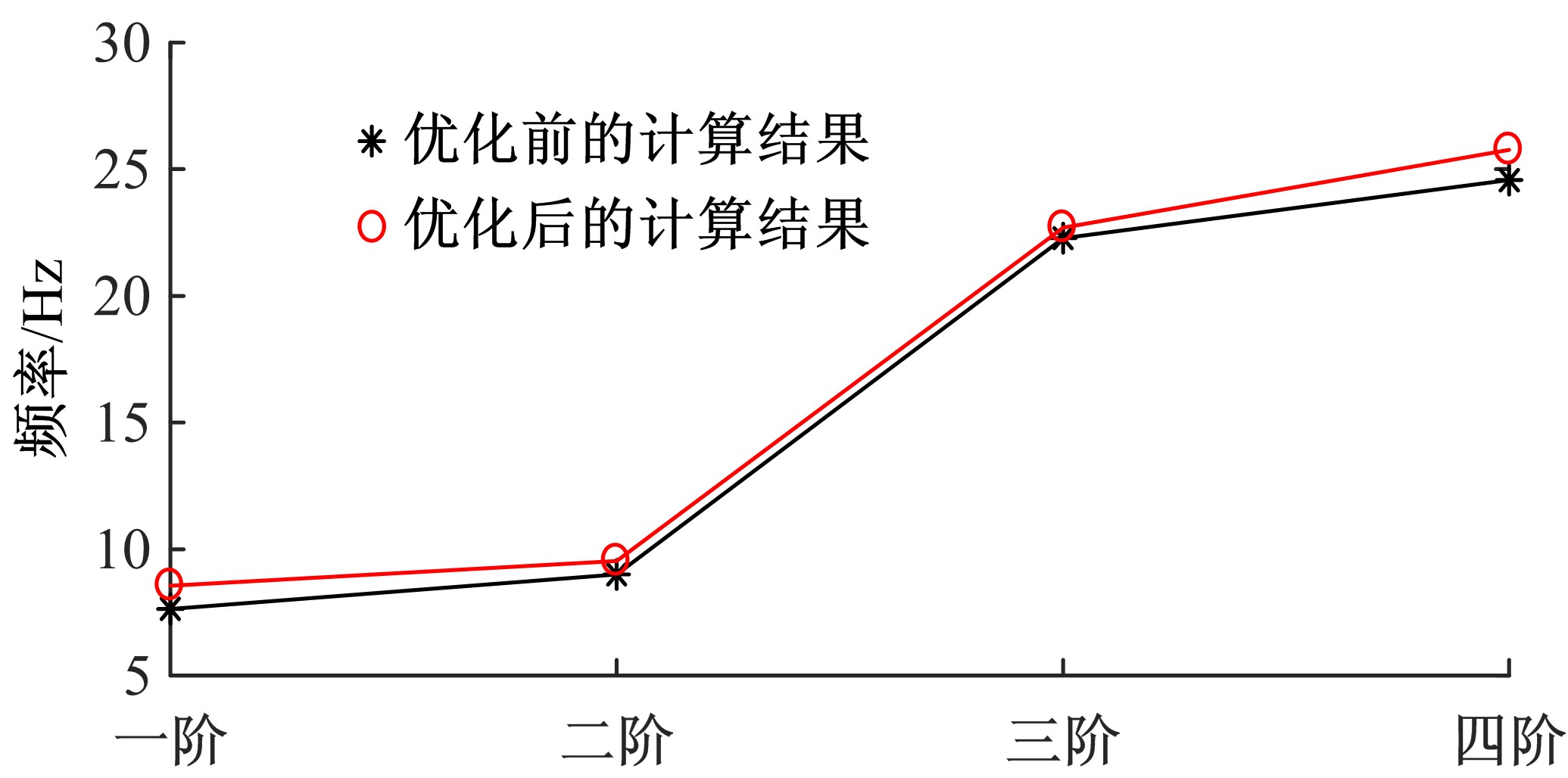
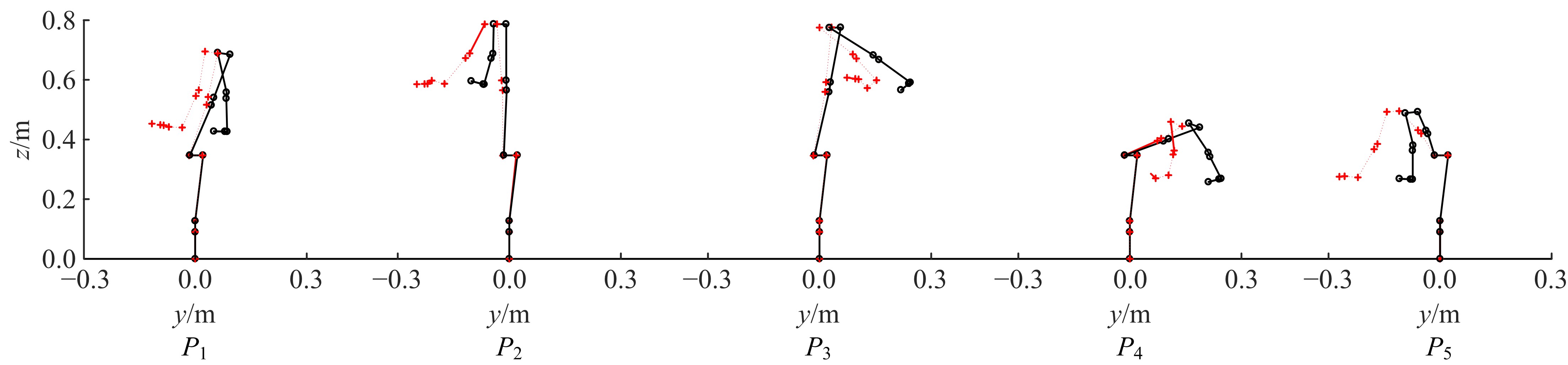
为解决时变位姿和建模精度对机器人结构优化的影响，提出了一种有限元与解析法相结合的机器人实时模态分析方法，能够实时、高效、高精度地获得机器人任意位姿下的固有频率和振型。同时为降低计算量，实现全域结构优化，基于正交设计提出了一种以机器人质量与全域一阶固有频率比（M/GF）为优化目标、以机器人结构尺寸为优化变量的全域动态性能结构优化设计方法。优化结果表明：优化后的M/GF指标比优化前提高了9.90%，优化后的全域一阶固有频率指标比优化前提高了0.91 Hz。

关键词: 机械电子工程, 正交设计, 协作机器人, 固有频率

Abstract:

To dispose of the influence of time-varying configurations and modeling accuracy on robot structural optimization， a Real-time Modal Analysis （RMA） method for collaborative robots was propose， which combines the finite element method and analytical method. This method could real-time obtain the natural frequencies and mode shapes of robots in any pose with high efficiency and precision. To reduce the calculating amount and realize global structure optimization， based on orthogonal design， a global structural optimization design method of collaborative robots was proposed with the structure parameters as optimization variables and the ratio of robot mass to the global first natural frequency index （M/GF） as optimization objective. The M/GF indexes of SHIR5 robot before and after optimization are calculated. The index after optimization is 9.90% higher than that before optimization， and the global first natural frequency index （GFNFI） is increased by 0.91Hz compared with that before optimization.

Key words: mechatronic engineering, orthogonal design, collaborative robots, natural frequency

中图分类号:

TP241

胡明伟,王洪光,潘新安. 基于正交设计的协作机器人全域结构优化设计[J]. 吉林大学学报(工学版), 2021, 51(1): 370-378.

Ming-wei HU,Hong-guang WANG,Xin-an PAN. Global structural optimization design of collaborative robots using orthogonal design[J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(1): 370-378.

图/表 10

图1

图2

图3

表1

表2

L27(313)正交试验表"

No.	T₁	T₂	T₃	T₄	T₅	T₆	T₇	T₈	T₉	T₁₀	T₁₁	L1	L2	M/kg	GFNFI/Hz	M/GF
1	1	1	1	1	1	1	1	1	1	1	1	1	1	21.06	7.90	2.67
2	1	1	1	1	2	2	2	2	2	2	2	2	2	21.62	8.21	2.63
3	1	1	1	1	3	3	3	3	3	3	3	3	3	22.20	8.37	2.65
4	1	2	2	2	1	1	1	2	2	2	3	3	3	21.41	7.89	2.71
5	1	2	2	2	2	2	2	3	3	3	1	1	1	21.93	8.22	2.67
6	1	2	2	2	3	3	3	1	1	1	2	2	2	21.84	8.26	2.64
7	1	3	3	3	1	1	1	3	3	3	2	2	2	21.77	7.94	2.74
8	1	3	3	3	2	2	2	1	1	1	3	3	3	21.67	8.01	2.71
9	1	3	3	3	3	3	3	2	2	2	1	1	1	22.19	8.34	2.66
10	2	1	2	3	1	2	3	1	3	2	1	2	3	21.73	7.97	2.73
11	2	1	2	3	2	3	1	2	1	3	2	3	1	21.70	8.16	2.66
12	2	1	2	3	3	1	2	3	2	1	3	1	2	21.85	8.23	2.65
13	2	2	3	1	1	2	3	2	1	3	3	1	2	21.67	8.07	2.68
14	2	2	3	1	2	3	1	3	2	1	1	2	3	21.75	8.33	2.61
15	2	2	3	1	3	1	2	1	3	2	2	3	1	21.76	7.86	2.77
16	2	3	1	2	1	2	3	3	2	1	2	3	1	21.78	8.23	2.64
17	2	3	1	2	2	3	1	1	3	2	3	1	2	21.78	8.04	2.71
18	2	3	1	2	3	1	2	2	1	3	1	2	3	21.72	8.18	2.66
19	3	1	3	2	1	3	2	1	2	3	1	3	2	21.78	7.97	2.73
20	3	1	3	2	2	1	3	2	3	1	2	1	3	21.93	8.08	2.72
21	3	1	3	2	3	2	1	3	1	2	3	2	1	21.93	8.24	2.66
22	3	2	1	3	1	3	2	2	3	1	3	2	1	21.89	8.18	2.68
23	3	2	1	3	2	1	3	3	1	2	1	3	2	21.87	8.25	2.65
24	3	2	1	3	3	2	1	1	2	3	2	1	3	21.87	8.04	2.72
25	3	3	2	1	1	3	2	3	1	2	2	1	3	21.84	8.33	2.62
26	3	3	2	1	2	1	3	1	2	3	3	2	1	21.86	7.88	2.77
27	3	3	2	1	3	2	1	2	3	1	1	3	2	21.92	8.20	2.67
R	0.14	0.09	0.27	0.11	0.11	0.37	0.04	0.54	0.38	0.29	0.19	0.10	0.06
Level	7	11	5	9	8	3	13	1	2	4	6	10	12
最优水平	1	1	1	1	3	3	2	3	1	1	1	1	3
T	0.32	0.11	1.09	0.18	0.20	2.31	0.03	6.77	2.42	1.34373	0.5120	0.155	0.06
Influence	No	No	No	No	No	No	No	Yes	No	No	No	No	No
Significance level 方正汇总行 $α = 0.1 ? ? ? ? ? ? ? ? ? F α (r - 1, n - r) = F 0.1 (2,24) = 2.54$

表2

图4

表3

图5

图6

图7

参考文献 21

1	―2:2011. Robots and robotic devices—Safety requirements for industrial robots part 2: robot systems and integration[S].
2	Alici G, Shirinzadeh B. Enhanced stiffness modeling, identification and characterization for robot manipulators[J]. IEEE Transactions on Robotics, 2005, 21(4): 554-564.
3	胡明伟, 王洪光, 潘新安, 等. 一种协作型机器人运动性能分析与仿真[J]. 智能系统学报, 2017, 12(1): 75-81.
	Hu Ming-wei,Wang Hong-guang,Pan Xin-an, et al. Analysis and simulation on kinematics performance of a collaborative robot[J]. CAAI Transactions on Intelligent Systems, 2017, 12(1): 75-81.
4	刘延杰, 吴明月, 王刚, 等. 硅片传输机器人手臂结构优化设计方法[J]. 机械工程学报, 2015, 51(1): 1-9.
	Liu Yan-jie, Wu Ming-yue, Wang Gang, et al. Method for structural optimization design of wafer handling robot arms[J]. Journal of Mechanical Engineering, 2015, 51(1): 1-9.
5	Hegde G S, Vinod M S, Shankar A, et al. Optimum dynamic design of flexible robotic manipulator[J]. International Journal of Mechanics and Materials in Design, 2009, 5(4): 315-325.
6	Kim B J, Yun D K, Lee S H, et al. Topology optimization of industrial robots for system-level stiffness maximization by using part-level metamodels[J]. Structural and Multidisciplinary Optimization, 2016, 54(4): 1061-1071.
7	Zhou L, Bai S. A new approach to design of a lightweight anthropomorphic arm for service applications[J]. Journal of Mechanisms and Robotics, 2015, 7(3): 1-12.
8	Luo H, Fu J, Wang P, et al. Design optimization of the ram structure of friction stir welding robot[J]. Mechanics of Advanced Materials and Structures, 2019: 1-11.
9	田野, 陈晓鹏, 贾东永, 等. 仿人机器人轻型高刚性手臂设计及运动学分析[J]. 机器人, 2011, 33(3): 332-339.
	Tian Ye, Chen Xiao-peng, Jia Dong-yong, et al. Design and kinematic analysis of a light weight and high stiffness manipulator for humanoid robots[J]. Robot, 2011, 33(3): 332-339.
10	Ning K P, Li D B, He F, et al. Research on the structural optimization design of ER300 palletizing robot[J]. The Open Automation and Control Systems Journal, 2015, 7(1): 1405-1414.
11	Nezhadali V. Multi-objective optimization of Industrial robots[D]. Linköping: Linköping University, 2015.
12	Yin H, Huang S, He M, et al. A unified design for lightweight robotic arms based on unified description of structure and drive trains[J]. International Journal of Advanced Robotic Systems, 2017, 14(4): 1-14.
13	Saravanan R, Ramabalan S, Ebenezer N G, et al. Evolutionary bi-criteria optimum design of robots based on task specifications[J]. The International Journal of Advanced Manufacturing Technology, 2009, 41(3): 386-406.
14	Zhu Y, Qiu J, Tani J. Simultaneous optimization of a two-link flexible robot arm[J]. Journal of Field Robotics, 2015, 18(1): 29-38.
15	Alessandro C, Rosario S. Elastodynamic optimization of a 3T1R parallel manipulator[J]. Mechanism and Machine Theory, 2014, 73: 184-196.
16	Zhang L, Song Y. Optimal design of the Delta robot based on dynamics[C]∥IEEE International Conference on Robotics and Automation, Shanghai, China, 2011, 43(9): 336-341.
17	Wang X, Zhang D, Zhao C, et al. Optimal design of lightweight serial robots by integrating topology optimization and parametric system optimization[J]. Mechanism and Machine Theory, 2019, 132: 48-65.
18	Hu M W, Wang H G, Pan X A, et al. Research on elastic deformation modeling of collaborative robots[C]∥IEEE International Conference on Robotics and Biomimetics, Macau, China, 2017: 2462-2467.
19	王新敏. ANSYS结构动力分析与应用[M]. 北京:人民交通出版社, 2014.
20	Slamani M, Nubiola A, Bonev I A, et al. Assessment of the positioning performance of an industrial robot[J]. Industrial Robot——an International Journal, 2012, 39(1): 57-68.
21	Hu M W, Wang H G, Pan X A, et al. Optimal synthesis of pose repeatability for collaborative robots based on the ISO 9283 standard[J]. Industrial Robot, 2019, 46(6): 812-818.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

[1]	姜继海,赵存然,张冠隆,车明阳. 航空煤油柱塞泵摩擦副涂层材料摩擦性能[J]. 吉林大学学报(工学版), 2021, 51(1): 147-153.
[2]	刘昌盛, 何清华, 张大庆, 李铁辉, 龚俊, 赵喻明. 混合动力挖掘机势能回收系统参数优化与试验[J]. 吉林大学学报(工学版), 2014, 44(2): 379-386.
[3]	龚俊, 何清华, 张大庆, 张云龙, 刘昌盛, 唐中勇. 混合动力叉车节能效果评价及能量回收系统试验[J]. 吉林大学学报(工学版), 2014, 44(01): 29-34.
[4]	张天霄, 刘昕晖, 张农. 液压溢流阀的振动分析[J]. 吉林大学学报(工学版), 2014, 44(01): 91-94.
[5]	韩志武, 吕尤, 董立春, 张俊秋, 牛士超, 马荣峰, 任露泉. 仿生表面形态齿轮的模态分析[J]. 吉林大学学报(工学版), 2010, 40(06): 1604-1608.
[6]	金文明,李华军,寇淑清,杨慎华. 装配式凸轮轴悬臂式数控装配机的机架模态分析[J]. 吉林大学学报(工学版), 2009, 39(增刊2): 319-0323.
[7]	赵淑芝,赵贝,朱永刚. 基于SP调查的出行方式选择模型与公交优先政策[J]. 吉林大学学报(工学版), 2009, 39(增刊2): 187-0190.
[8]	苏铁坚, 管爱华, 麦莉. 受纵向分布压力的弹性薄板的动力分析[J]. 吉林大学学报(工学版), 2000, (3): 72-74.
[9]	刘寒冰, 龚国庆, 魏媛. 改进的r-收敛和h-收敛自适应有限元方法[J]. 吉林大学学报(工学版), 2000, (3): 56-60.

基于正交设计的协作机器人全域结构优化设计

Global structural optimization design of collaborative robots using orthogonal design

RICH HTML

PDF (PC)

摘要/Abstract

引用本文

使用本文

图/表 10

参考文献 21

相关文章 9

Metrics

本文评价

推荐阅读 0

水平	T₁	T₂	T₃	T₄	T₅	T₆	T₇	T₈	T₉	T₁₀	T₁₁	L1	L2
1	2.5	2	1.5	3.5	3.5	3.5	3.5	2.5	2.5	2.2	2.2	223	222
2	3	2.5	2	4	4	4	4	3	3	2.5	2.5	203	202
3	3.5	3	2.5	4.5	4.5	4.5	4.5	3.5	3.5	2.8	2.8	183	182

	T₁	T₂	T₃	T₄	T₅	T₆	T₇	T₈	T₉	T₁₀	T₁₁	L1	L2	M/kg	GFNFI/Hz	M/GF
原始值	3	3	2.5	4.5	3.5	3.5	3.5	2.5	3.5	2.8	2.8	183	222	21.60	7.65	2.82
优化值	2.5	2	1.5	3.5	4.5	4.5	4	3.5	2.5	2.2	2.2	223	182	21.78	8.56	2.54

水平	T₁	T₂	T₃	T₄	T₅	T₆	T₇	T₈	T₉	T₁₀	T₁₁	L1	L2
1	2.5	2	1.5	3.5	3.5	3.5	3.5	2.5	2.5	2.2	2.2	223	222
2	3	2.5	2	4	4	4	4	3	3	2.5	2.5	203	202
3	3.5	3	2.5	4.5	4.5	4.5	4.5	3.5	3.5	2.8	2.8	183	182

水平	T₁	T₂	T₃	T₄	T₅	T₆	T₇	T₈	T₉	T₁₀	T₁₁	L1	L2
1	2.5	2	1.5	3.5	3.5	3.5	3.5	2.5	2.5	2.2	2.2	223	222
2	3	2.5	2	4	4	4	4	3	3	2.5	2.5	203	202
3	3.5	3	2.5	4.5	4.5	4.5	4.5	3.5	3.5	2.8	2.8	183	182