吉林大学学报(工学版) ›› 2024, Vol. 54 ›› Issue (9): 2451-2459.doi: 10.13229/j.cnki.jdxbgxb.20221393

• 车辆工程·机械工程 • 上一篇    

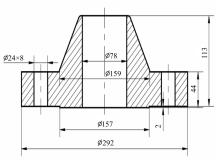
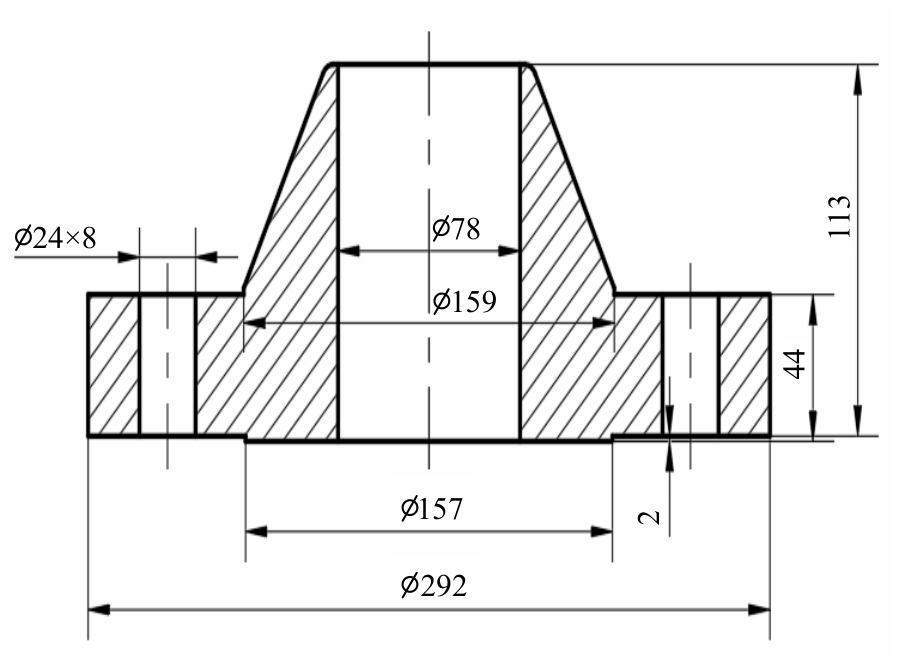
凸面法兰连接下的螺栓载荷均匀性分析

李玲(),杜旭阳,王晶晶,阮晓光(),蔡安江   

  1. 西安建筑科技大学 机电工程学院，西安 710055
  • 收稿日期:2022-11-01 出版日期:2024-09-01 发布日期:2024-10-28
  • 通讯作者: 阮晓光 E-mail:liling@xauat.edu.cn;rxgly@126.com
  • 作者简介:李玲（1981-），男，教授，博士.研究方向：机械动力学和接触力学.E-mail：liling@xauat.edu.cn
  • 基金资助:
    国家自然科学基金项目(51975449);陕西省重点研发计划项目(2021GY-309)

Analysis of bolt load uniformity under convex flange connection

Ling LI(),Xu-yang DU,Jing-jing WANG,Xiao-guang RUAN(),An-jiang CAI   

  1. School of Mechanical and Electrical Engineering，Xi'an University of Architecture and Technology，Xi'an 710055，China
  • Received:2022-11-01 Online:2024-09-01 Published:2024-10-28
  • Contact: Xiao-guang RUAN E-mail:liling@xauat.edu.cn;rxgly@126.com

RICH HTML

 2   

PDF (PC)

37

摘要：

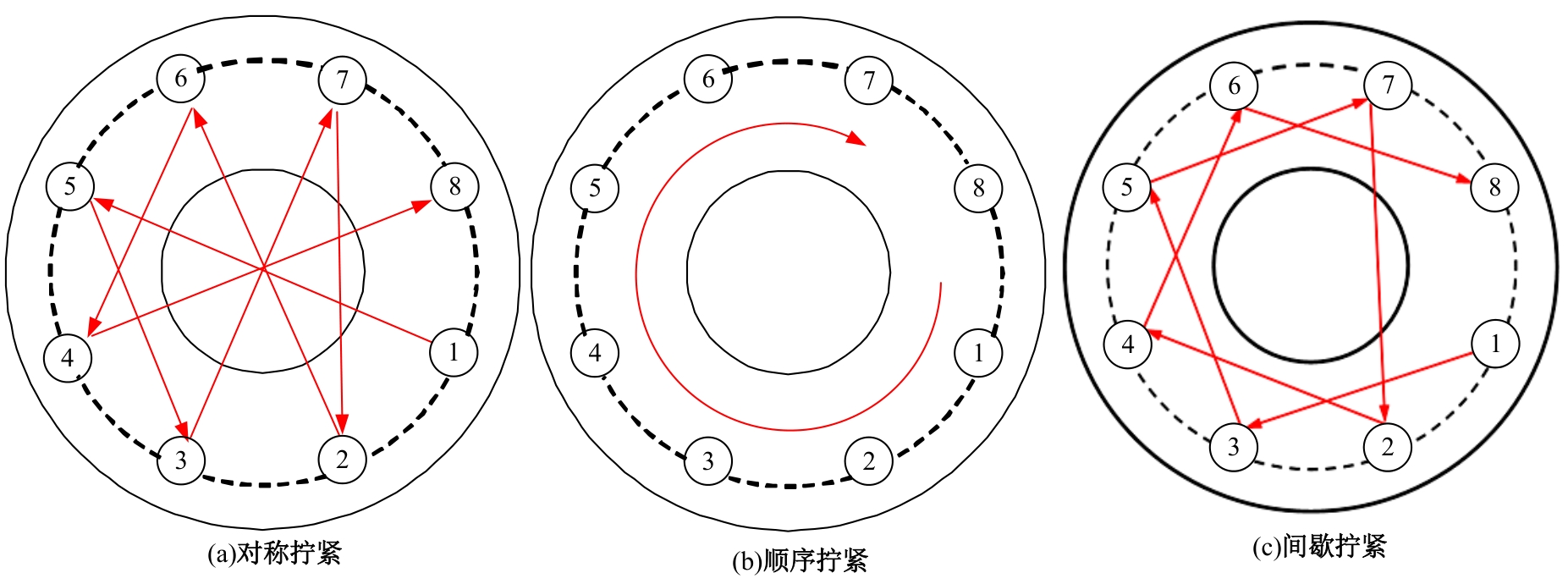
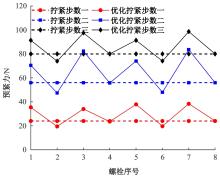
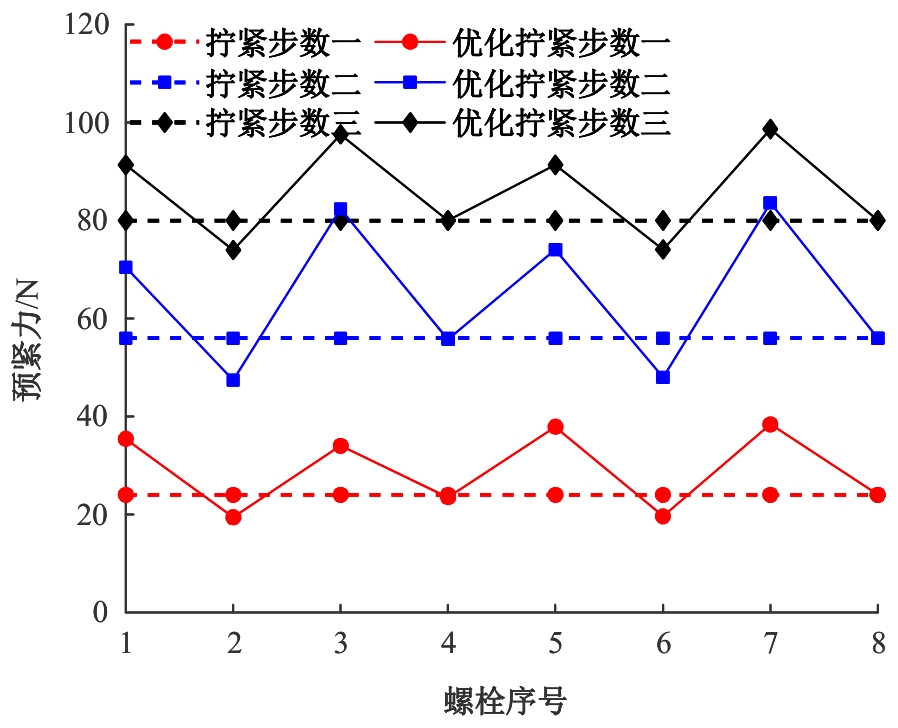
通过构建弹性相互作用模型，优化凸面法兰连接的螺栓预紧力均匀性。将一次弹性相互作用系数法扩展至多次拧紧过程，通过解析模型预测各拧紧步数下所有螺栓的初始预紧力。建立三维有限元模型验证其准确性，并探究拧紧顺序与步数的影响。结果表明：对称拧紧三步法可最小化弹性相互作用，提升预紧力均匀性。考虑弹性相互作用的模型进一步优化了均匀性，更接近目标值。该方法有效解决了预紧力分散问题，为螺栓法兰结构的安全可靠性设计提供了科学依据。

关键词: 螺栓法兰连接, 弹性相互作用, 预紧力, 载荷均匀性

Abstract:

The study aims to optimize the uniformity of bolt preload by constructing elastic interaction models and optimizing the flange connection with convex surfaces. The elastic interaction coefficient method is extended to multiple tightening processes， and the initial preload of all bolts at each tightening step is predicted by the analytical model. A three-dimensional finite element model is established to verify its accuracy and explore the effects of tightening sequence and steps. The results show that the symmetric tightening method of three steps minimizes the elastic interaction and improves the uniformity of preload. The model considering elastic interaction further optimizes the uniformity， closer to the target value. This method effectively solves the problem of uneven preload and provides scientific basis for the safety and reliability design of bolt flange structures.

Key words: bolted flange connection, elastic interaction, preload, load uniformity

中图分类号: 

  • TG95

图1

NPS4-900型法兰二维图"

图2

螺栓法兰连接结构有限元模型"

表1

仿真工况"

序号加载方式备注
1拧紧顺序

对称拧紧

顺序拧紧

间歇拧紧

2拧紧步数

一步

三步

图3

拧紧顺序"

图4

对称拧紧的数值与实验分析"

图5

间歇拧紧螺栓预紧力"

图6

顺序拧紧螺栓预紧力"

图7

对称拧紧螺栓预紧力"

图8

一次拧紧螺栓预紧力"

图9

三次拧紧螺栓预紧力"

图10

每个拧紧步数各个螺栓施加的预紧力"

图11

考虑弹性相互作用与不考虑弹性相互作用最终预紧力对比"

1 黄贤振,孙楷铂,栾晓刚,等.螺栓预紧连接可靠性灵敏度分析[J]. 吉林大学学报: 工学版, 2023, 53(8):2219-2226.
Huang Xian-zhen, Sun Kai-bo, Luan Xiao-gang, et al.Reliability sensitivity analysis of bolt pre-tightening connection[J]. Journal of Jilin University (Engineering and Technology Edition), 2023,53(8):2219-2226.
2 Bickford J H. Introduction to the Design and Behavior of Bolted Joints: Non-Gasketed Joints[M]. Florida: CRC Press, 2007.
3 Bickford J H, Nassar S. Handbook of Bolts and Bolted Joints[M].Florida: CRC Press,1998.
4 Bibel G D, Ezell R M. Bolted flange assembly: preliminary elastic interaction data and improved bolt-up procedures[J]. Bulletin Welding Research Council, 1996,408:No.379774.
5 Bibel G D, Ezell R M. An improved flange bolt-up procedure using experimentally determined elastic interaction coefficients[J]. Journal of Pressure Vessel Technology, 1992,114(4):439-443.
6 Nassar S A, Alkelani A A. Clamp load loss due to elastic interaction and gasket creep relaxation in bolted joints[J]. Journal of Pressure Vessel Technology, 2006, 128(3): 394-401.
7 Alkelani A A, Nassar S A, Housari B A. Formulation of elastic interaction between bolts during the tightening of flat-face gasketed joints[J]. Journal of Mechanical Design, 2009,131(2): No.21004.
8 Nassar S A, Yang X. Novel formulation of bolt elastic interaction in gasketed joints[J]. Journal of Pressure Vessel Technology, 2009,131(5):No.3151814.
9 Fukuoka T, Takaki T. Finite element simulation of bolt-up process of pipe flange connections with spiral wound gasket[J]. Journal of Pressure Vessel Technology, 2003,125(4):371-378.
10 Takaki T, Fukuoka T. Systematical FE analysis of bolt assembly process of pipe flange connections[C]∥ASME Pressure Vessels and Piping Conference,Atlanta,USA,2002, 19442:147-152.
11 Takaki T, Fukuoka T. Effective bolting up procedure using finite element analysis and elastic interaction coefficient method[C]∥ASME Pressure Vessels and Piping Conference, Atlanta, USA, 2004, 46733:155-162.
12 Abid M, Hussain S. Bolt preload scatter and relaxation behavior during tightening a 4 in 900#flange joint with spiral wound gasket[J]. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering, 2008,222(2):123-134.
13 Nassar S A, Wu Z J, Yang X J.Achieving uniform clamp load in gasketed bolted joints using a nonlinear finite element model[J]. Journal of Pressure Vessel Technology, 2010,132(3): No.031205.
14 陈成军, 杨国庆, 常东方, 等.基于有限元法的螺栓组连接弹性相互作用研究[J].武汉理工大学学报, 2011, 33(10): 131-135.
Chen Cheng-jun, Yang Guo-qing, Chang Dong-fang, et al. FEM based elastic interaction analysis of assembly and fastening[J]. Journal of Wuhan University of Technology, 2011,33(10): 131-135.
15 Abasolo M, Aguirrebeitia J, Aviles R, et al. A tetraparametric metamodel for the analysis and design of bolting sequences for wind generator flanges[J]. Journal of Pressure Vessel Technology, 2011,133(4): No.4002541.
16 Abasolo M, Aguirrebeitia J, Aviles R, et al. Methodology for the optimization of bolting sequences for wind generator flanges[J]. Journal of Pressure Vessel Technology, 2014, 136(6): No.61202.
17 Wang Y Q, Wu J K, Liu H B, et al. Modeling and numerical analysis of multi-bolt elastic interaction with bolt stress relaxation[J]. Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science, 2016,230(15): 2579-2587.
18 Wang Y Q, Wu J K, Liu H B, et al. Analysis of elastic interaction stiffness and its effect on bolt preloading[J]. International Journal of Mechanical Sciences, 2017,130: 307-314.
19 Zhu L B, Bouzid A, Hong J, et al. Numerical and experimental study of elastic interaction in bolted flange joints[J]. Journal of Pressure Vessel Technology, 2017,139(2): No.21211.
20 Zhu L B, Bouzid A, Hong J, et al. Elastic interaction in bolted flange joints: an analytical model to predict and optimize bolt load[J]. Journal of Pressure Vessel Technology, 2018,140(4): No.4040421.
21 Kurfess T R, Saldana C, Saleeby K, et al. A review of modern communication technologies for digital manufacturing processes in industry 4.0[J]. Journal of Manufacturing Science and Engineering, 2020, 142(11): No.110815.
22 Li B, Chen H, Jin T. Support vector regression for optimal robotic force control assembly[J]. Journal of Manufacturing Science and Engineering, 2020,142(1):No.011007.
23 Wang Z, Liu P, Xiao Y, et al. A data driven approach for process optimization of metallic additive manufacturing under uncertainty[J]. Journal of Manufacturing Science and Engineering, 2019,141(8): No.081004.
[1] 陶文斌,侯俊领,陈铁林,唐彬. 高预紧力后张法全长锚固支护力学分析[J]. 吉林大学学报(工学版), 2020, 50(2): 631-640.
[2] 王智. 月基二维转台轴承预紧力和系统刚度计算[J]. 吉林大学学报(工学版), 2015, 45(6): 1831-1835.
[3] 杨佐卫,殷国富,尚欣,姜华,钟开英. 高速电主轴热态特性与动力学特性耦合分析模型[J]. 吉林大学学报(工学版), 2011, 41(01): 100-0105.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
版权所有 © 《吉林大学学报(工学版)》编辑部
地址：长春市人民大街5988号　电话：+86-431-85095297　传真：+86-431-85094074　E-mail: xbgxb@jlu.edu.cn
本系统由北京玛格泰克科技发展有限公司设计开发