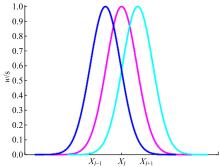
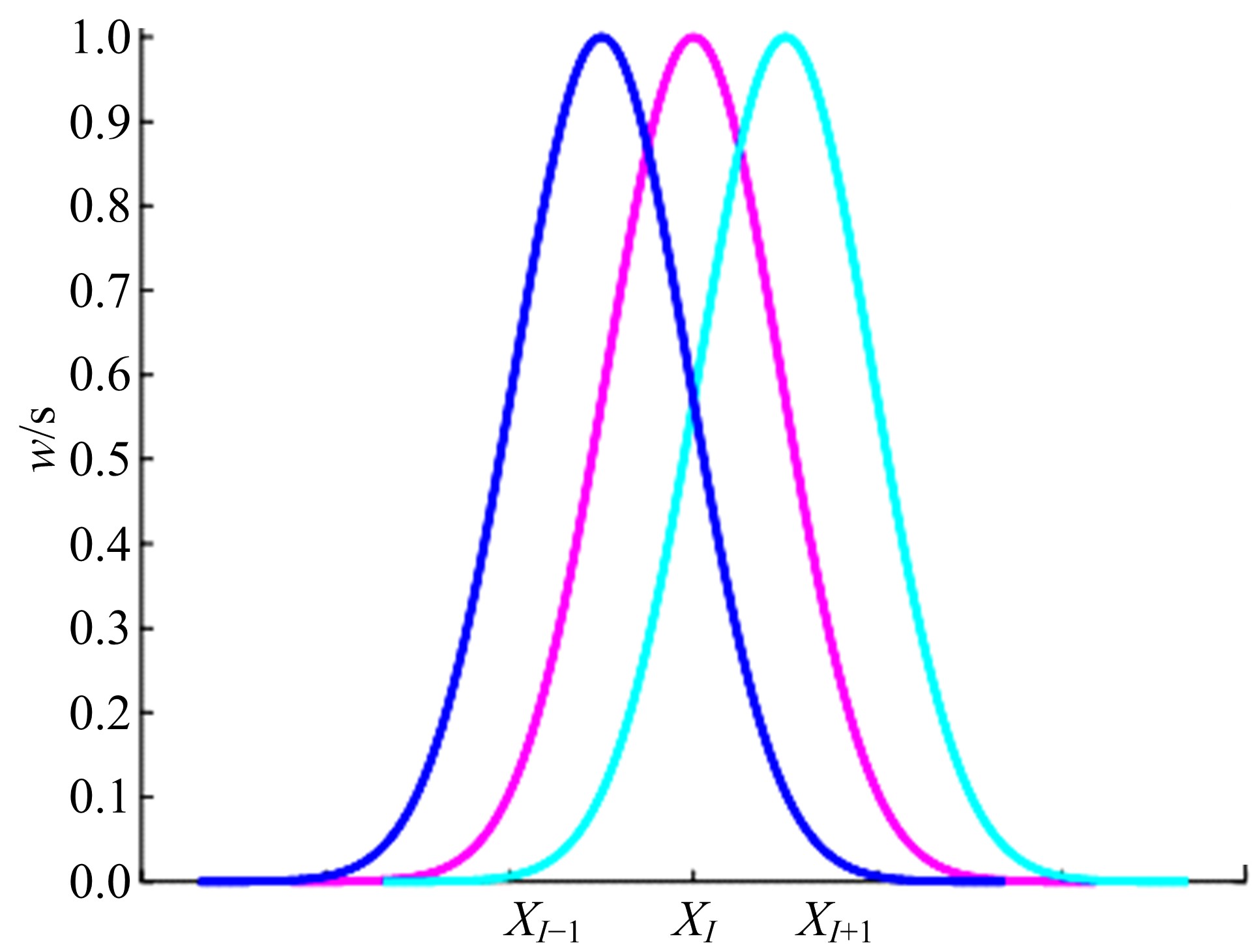
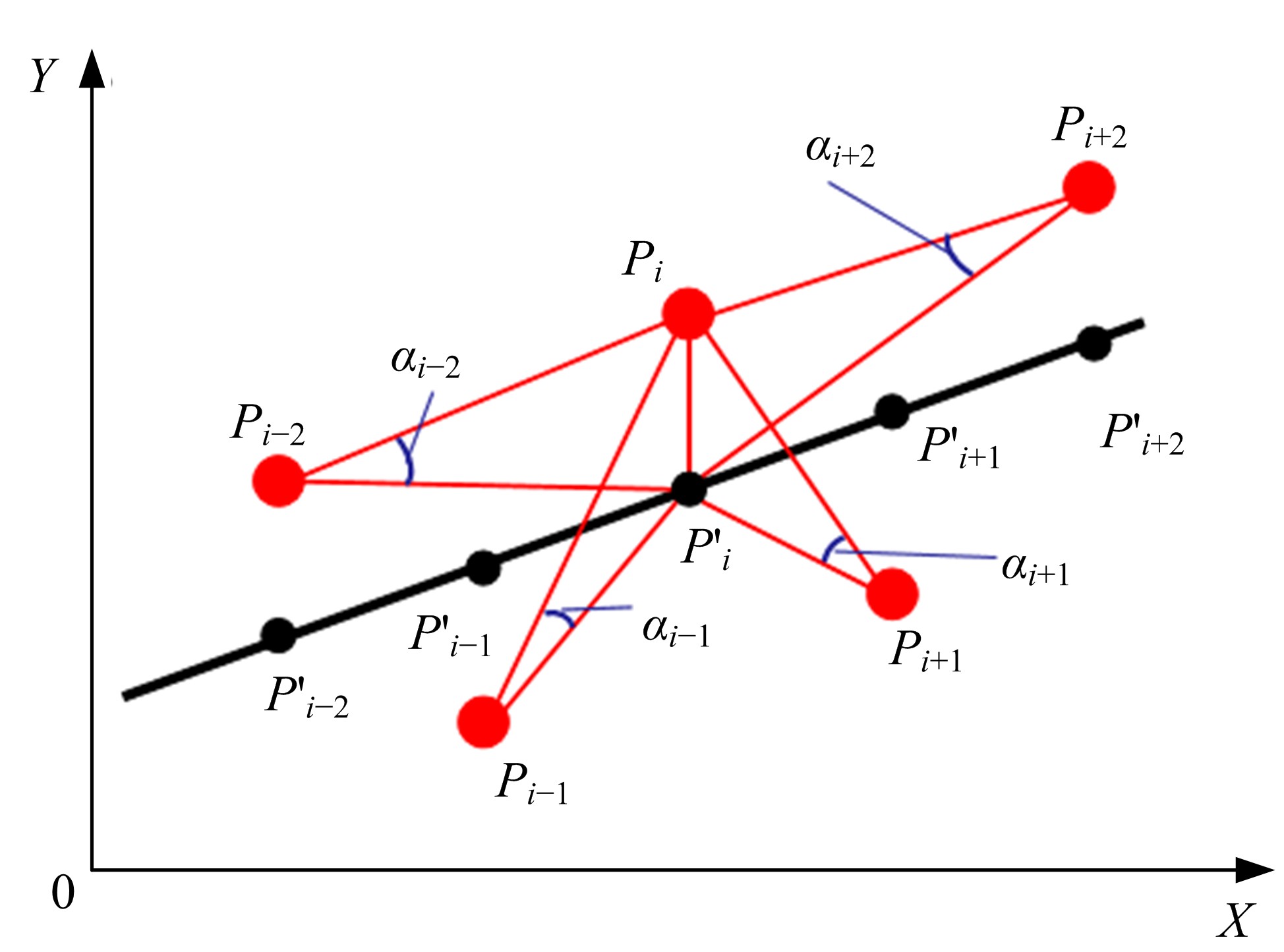
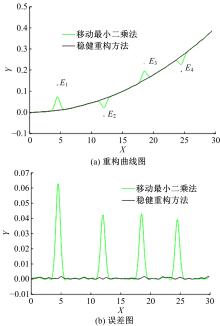
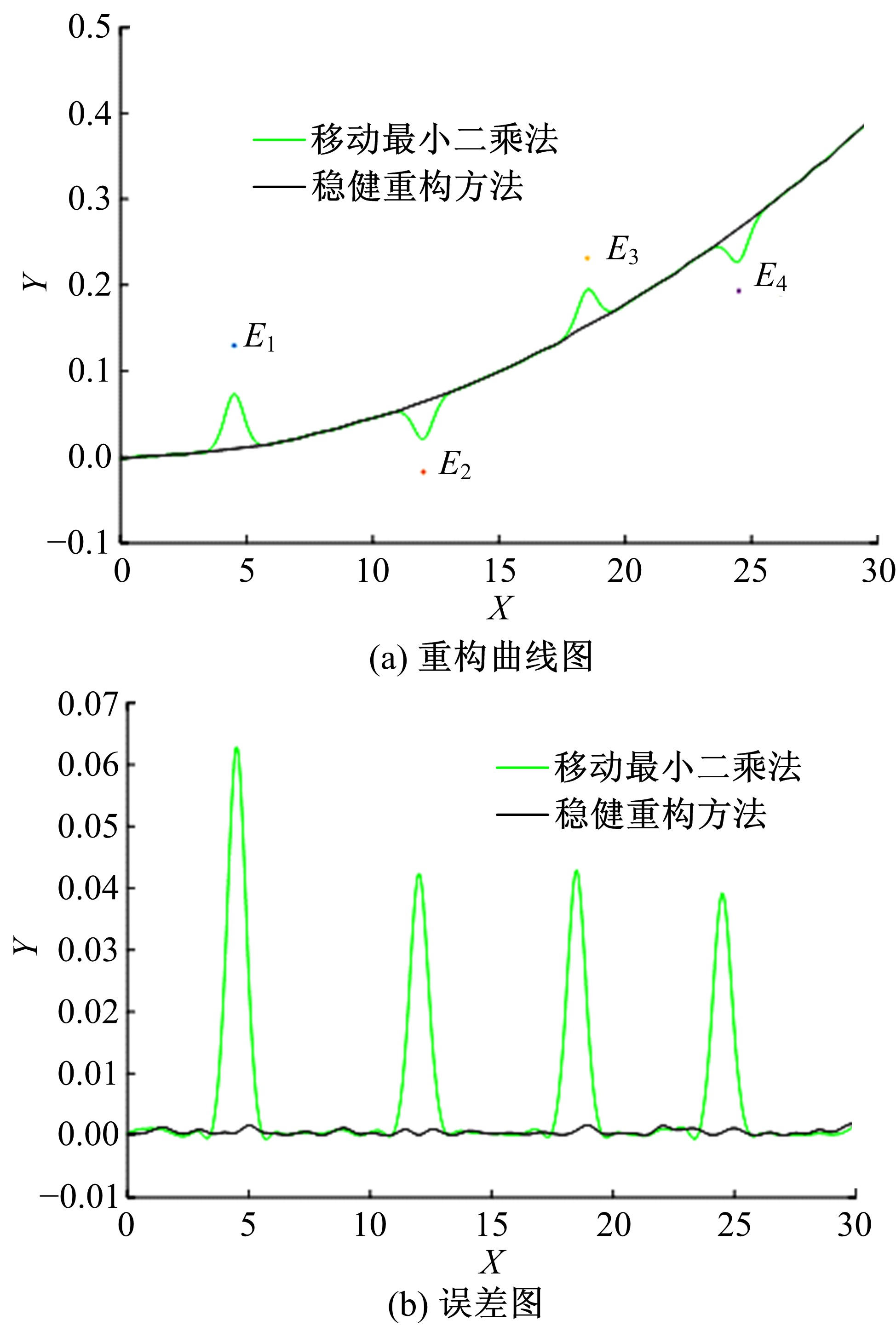
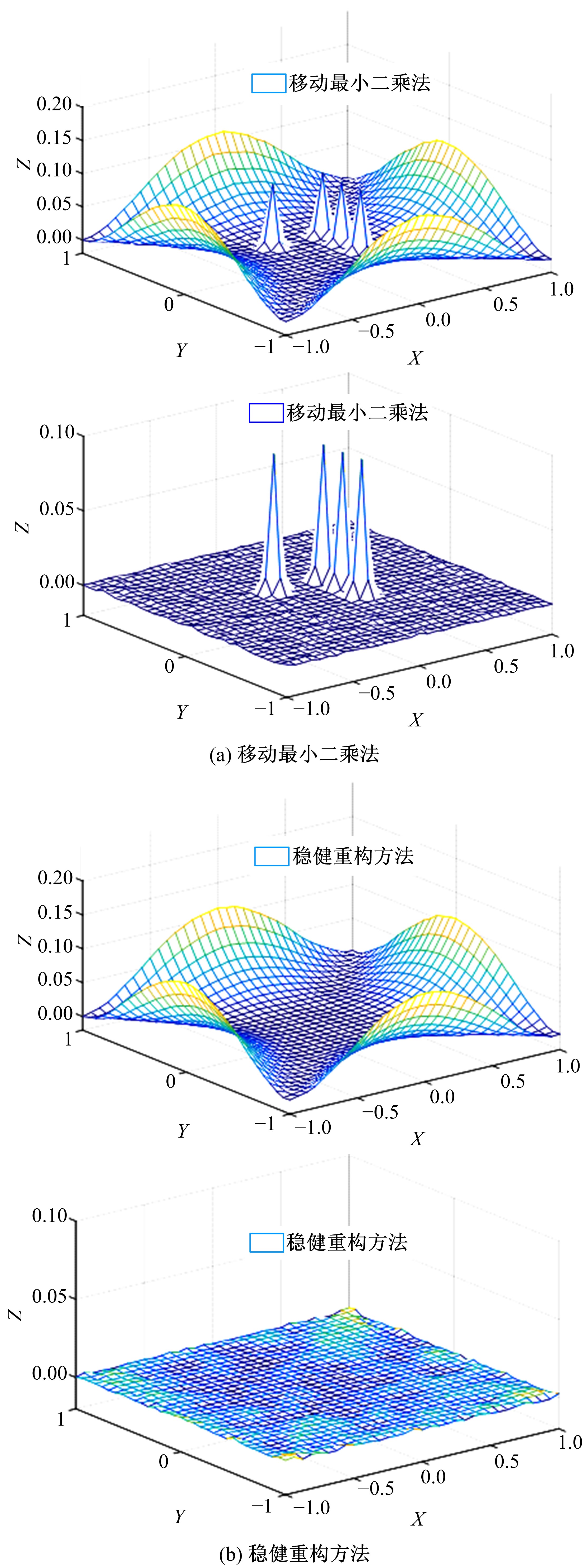
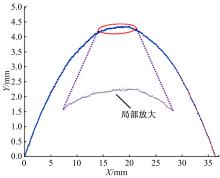
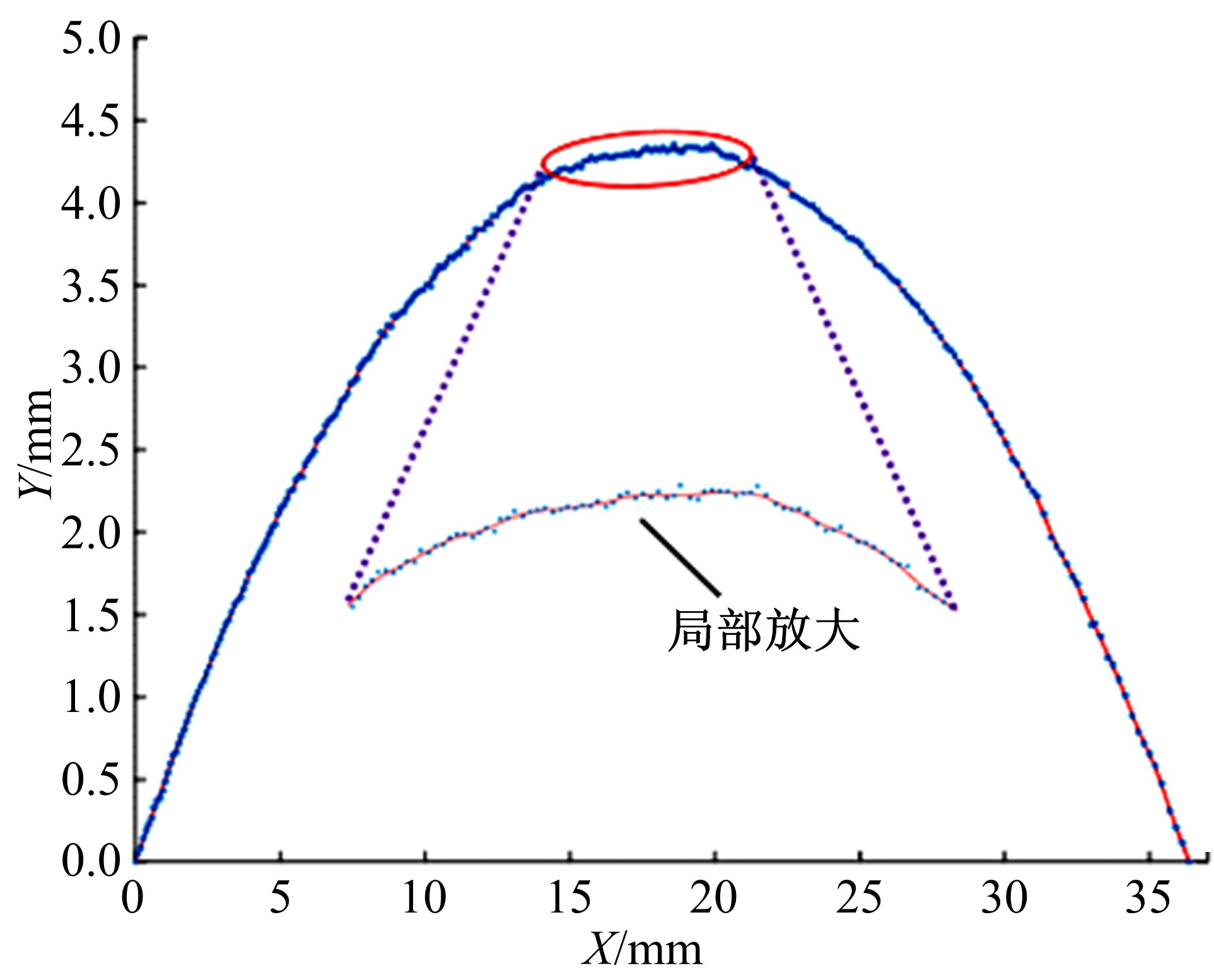
Journal of Jilin University(Engineering and Technology Edition) ›› 2021, Vol. 51 ›› Issue (2): 685-691.doi: 10.13229/j.cnki.jdxbgxb20191050
Robust reconstruction method based on moving least squares algorithm
Tian-qi GU( ),Chen-jie HU,Yi TU,Shu-wen LIN
),Chen-jie HU,Yi TU,Shu-wen LIN
- College of Mechanical Engineering and Automation,Fuzhou University,Fuzhou 350116,China
CLC Number:
- TP391.9
| 1 | 张雄, 刘岩, 马上. 无网格法的理论及应用[J]. 力学进展, 2009, 39(1): 1-36. |
| Zhang Xiong, Liu Yan, Ma Shang. Theory and application of meshless method[J]. Progress in Mechanics, 2009, 39(1): 1-36. | |
| 2 | Lancaster P,Salkauskas K. Surfaces generated by moving least squares methods[J]. Mathematics Computation, 1981, 37: 141-158. |
| 3 | 韩加坤. 无网格法中MLS参数的选取[J]. 数学学习与研究, 2016(23): 145,147. |
| Han Jia-kun. Selection of MLS parameters in meshless method[J]. Mathematics Learning and Research, 2016(23): 145,147. | |
| 4 | 王青青, 李小林. 基于比例移动最小二乘近似的误差分析[J]. 应用数学和力学, 2017, 38(11): 1289-1299. |
| Wang Qing-qing, Li Xiao-lin. Error analysis based on proportional moving least square approximation[J]. Applied Mathematics and Mechanics, 2017, 38(11): 1289-1299. | |
| 5 | Carlos Z. Good quality point sets and error estimates for moving least square approximations[J]. Applied Numerical Mathematics, 2003, 47(3): 575-585. |
| 6 | 袁占斌, 聂玉峰, 欧阳洁. 基于泰勒基函数的移动最小二乘法及误差分析[J]. 数值计算与计算机应用, 2012, 33(1): 25-31. |
| Yuan Zhan-bin, Nie Yu-feng, Jie Ou-yang. Moving least square method and error analysis based on taylor basis function[J]. Numerical Computing and Computer Applications, 2012, 33(1): 25-31. | |
| 7 | 顾天奇, 张雷, 冀世军, 等. 封闭离散点的曲线拟合方法[J]. 吉林大学学报: 工学版, 2015, 45(2): 437-441. |
| Gu Tian-qi, Zhang Lei, Ji Shi-jun, et al. Curve fitting method for closed discrete points[J]. Journal of Jilin University (Engineering and Technology Edition), 2015, 45(2): 437-441. | |
| 8 | 李世飞, 王平, 沈振康. 利用移动最小二乘法进行深度图像曲面拟合[J]. 吉林大学学报: 工学版, 2010, 40(1): 229-233. |
| Li Shi-fei, Wang Ping, Shen Zhen-kang. Range image surface fitting via moving least squares methods[J]. Journal of Jilin University (Engineering and Technology Edition), 2010, 40(1): 229-233. | |
| 9 | Liu D, Cheng Y M. The interpolating element-freeGalekin (IEFG) method for three-dimensional pote-ntial problems[J]. Engineering Analysis with Boun-Dary Elements, 2019, 108: 115-123. |
| 10 | Wang Q, Zhou W, Feng Y T, et al. An adaptive orthogonal improved interpolating moving least-square method and a new boundary element-free method[J]. Applied Mathematics and Computation, 2019, 353: 347-370. |
| 11 | 崔鑫, 闫秀天, 李世鹏. 保持特征的散乱点云数据去噪[J]. 光学精密工程, 2017, 25(12): 3169-3178. |
| Cui Xin, Yan Xiu-tian, Li Shi-peng. Denoising of scattered point cloud data with preserved features[J]. Optical Precision Engineering, 2017, 25(12): 3169-3178. | |
| 12 | Liu D L, Shi Y, Tian Y J, et al. Ramp loss least squares support vector machine[J]. Journal of Computation Science, 2016, 14: 61-68. |
| 13 | Suykens J A K, Brabanter J D, Lukas L, et al. Weighted least squares support vector m-achines: robustness and sparse approximation[J]. Neurocomputing, 2002, 48(1-4): 85-105. |
| 14 | Lin Y L, Hsieh J G, Jeng J H, et al. On least trimmed squares neural networks[J]. Neurocomputing, 2015, 161: 107-112. |
| 15 | Yang B, Shao Q M, Pan L, et al. A study on regularized weighted least square support vector classifier[J]. Pattern Recognition Letters, 2018, 108: 48-55. |
| 16 | Chen C F, Yan C Q, Li Y Y. A robust weighted least squares support vector regression based on least trimmed squares[J]. Neurocomputing, 2015, 168: 941-946. |
| 17 | Wen W, Hao Z F, Yang X W. Robust least squares support vector machine based on recursive outlier elimination[J]. Soft Computing, 2010, 14(11): 1241-1251. |
| 18 | Grand R J, Habibullah A C, Adam W, et al. Modified moving least squares with polynomial bases for scattered data approximation[J]. Applied Mathematics and Computation, 2015, 266: 893-902. |
| 19 | 李睿, 林海荣, 吴小燕. 基于稳健移动最小二乘法的点云数据拟合[J]. 测绘与空间地理信息, 2017, 40(5): 122-124. |
| Li Rui, Lin Hai-rong, Wu Xiao-yan. Point cloud data fitting based on robust moving least square method[J]. Mapping and Spatial Geographic Information, 2017, 40(5): 122-124. | |
| 20 | 范晓明, 罗词金, 徐学科, 等. 光学非球面三坐标测量中的像散补偿[J]. 光学精密工程, 2016, 24(12): 3012-3019. |
| Fan Xiao-ming, Luo Ci-jin, Xu Xue-ke, et al. Astigmatic compensation in optical aspheric three-coordinate measurement[J]. Optical Precision Engineering, 2016, 24(12): 3012-3019. |
| [1] | Xiao-hui WEI,Chang-bao ZHOU,Xiao-xian SHEN,Yuan-yuan LIU,Qun-chao TONG. Accelerating CALYPSO structure prediction with machine learning [J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(2): 667-676. |
| [2] | Xiao-dong ZHU,Qi-xian ZHANG,Yuan-ning LIU, WU-di,Zu-kang WU,Chao-qun WANG,Xin-long LI. Iris recognition based on multi⁃direction local binary pattern and stable feature [J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(2): 650-658. |
| [3] | Xiao-yu WANG,Xin-hao HU,Chang-lin HAN. Face pencil drawing algorithms based on generative adversarial network [J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(1): 285-292. |
| [4] | Yuan SONG,Dan-yuan ZHOU,Wen-chang SHI. Method to enhance security function of OpenStack Swift cloud storage system [J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(1): 314-322. |
| [5] | Ming FANG,Wen-qiang CHEN. Face micro-expression recognition based on ResNet with object mask [J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(1): 303-313. |
| [6] | Yang LI,Shuo LI,Li-wei JING. Estimate model based on Bayesian model and machine learning algorithms applicated in financial risk assessment [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(5): 1862-1869. |
| [7] | Bing-hai ZHOU,Zhao-xu HE. Dynamic material handling scheduling for mixed⁃model assembly lines based on line⁃integrated supermarkets [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(5): 1809-1817. |
| [8] | Lei JIANG,Ren-chu GUAN. Design of fuzzy comprehensive evaluation system for talent quality based on multi⁃objective evolutionary algorithm [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(5): 1856-1861. |
| [9] | Hong-wei ZHAO,Xiao-han LIU,Yuan ZHANG,Li-li FAN,Man-li LONG,Xue-bai ZANG. Clothing classification algorithm based on landmark attention and channel attention [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(5): 1765-1770. |
| [10] | Nai-yan GUAN,Juan-li GUO. Component awareness adaptive model based on attitude estimation algorithms [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(5): 1850-1855. |
| [11] | Xiang-jiu CHE,You-zheng DONG. Improved image recognition algorithm based on multi⁃scale information fusion [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(5): 1747-1754. |
| [12] | Zhou-zhou LIU,Wen-xiao YIN,Qian-yun ZHANG,Han PENG. Sensor cloud intrusion detection based on discrete optimization algorithm and machine learning [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(2): 692-702. |
| [13] | Xiao-hui WANG,Lu-shen WU,Hua-wei CHEN. Denoising of scattered point cloud data based on normal vector distance classification [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(1): 278-288. |
| [14] | Xiao-dong ZHANG,Xiao-jun XIA,Hai-feng LYU,Xu-chao GONG,Meng-jia LIAN. Dynamic load balancing of physiological data flow in big data network parallel computing environment [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(1): 247-254. |
| [15] | Man CHEN,Yong ZHONG,Zhen-dong LI. Multi-focus image fusion based on latent low⁃rank representation combining low⁃rank representation [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(1): 297-305. |
|
||