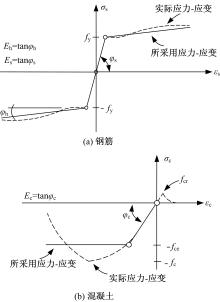
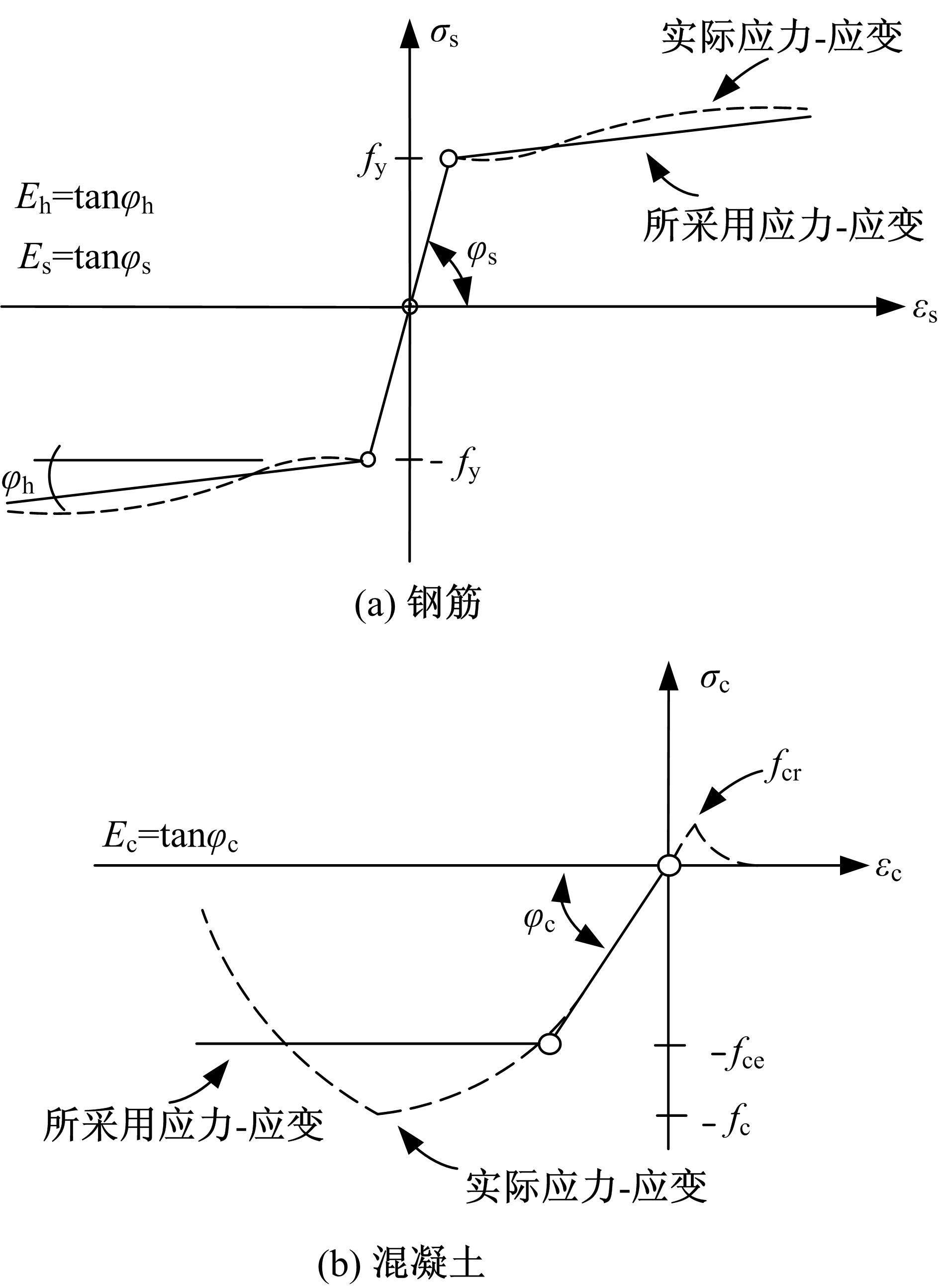
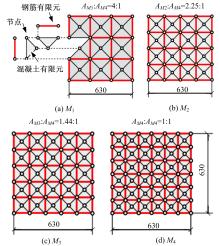
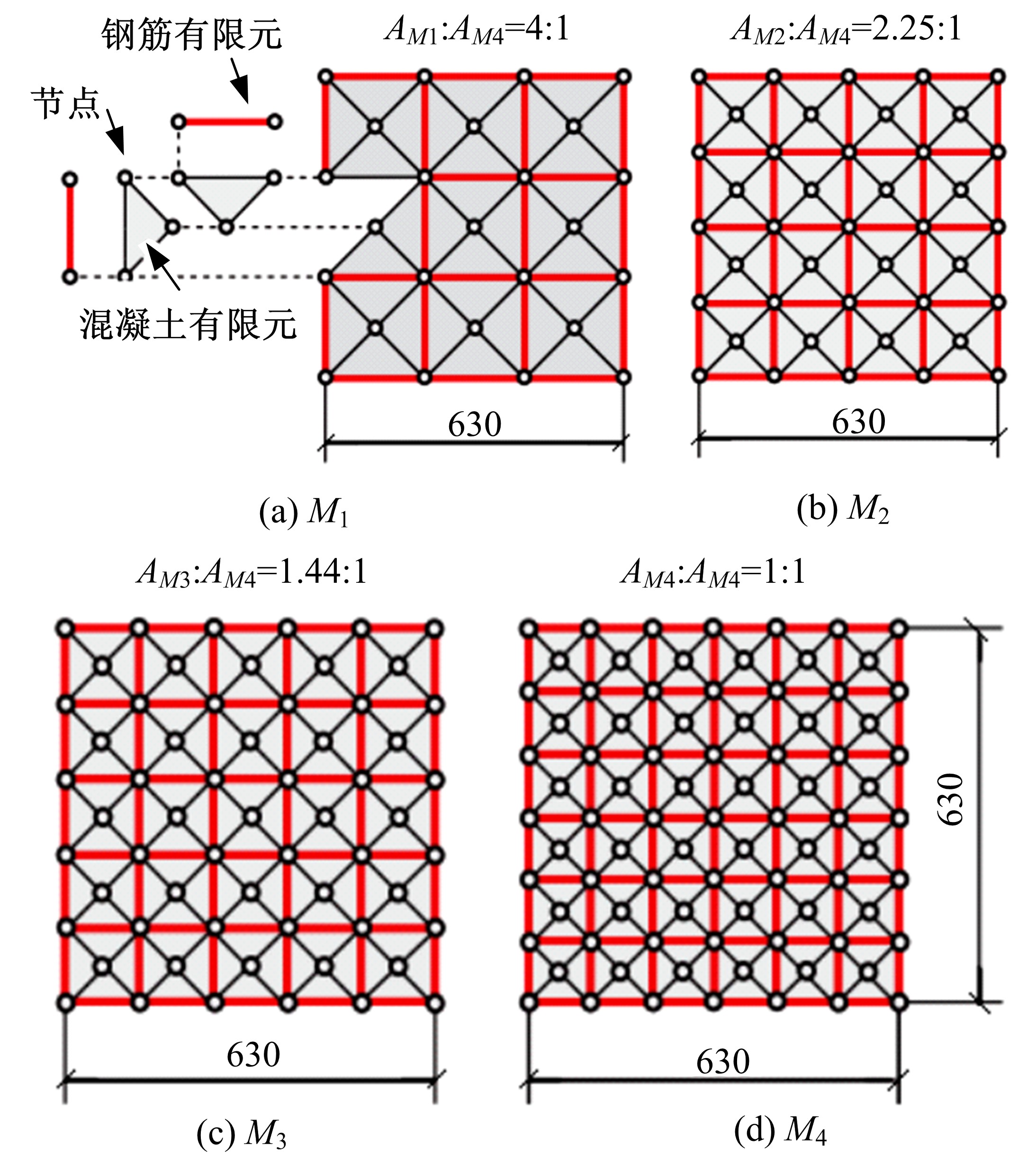
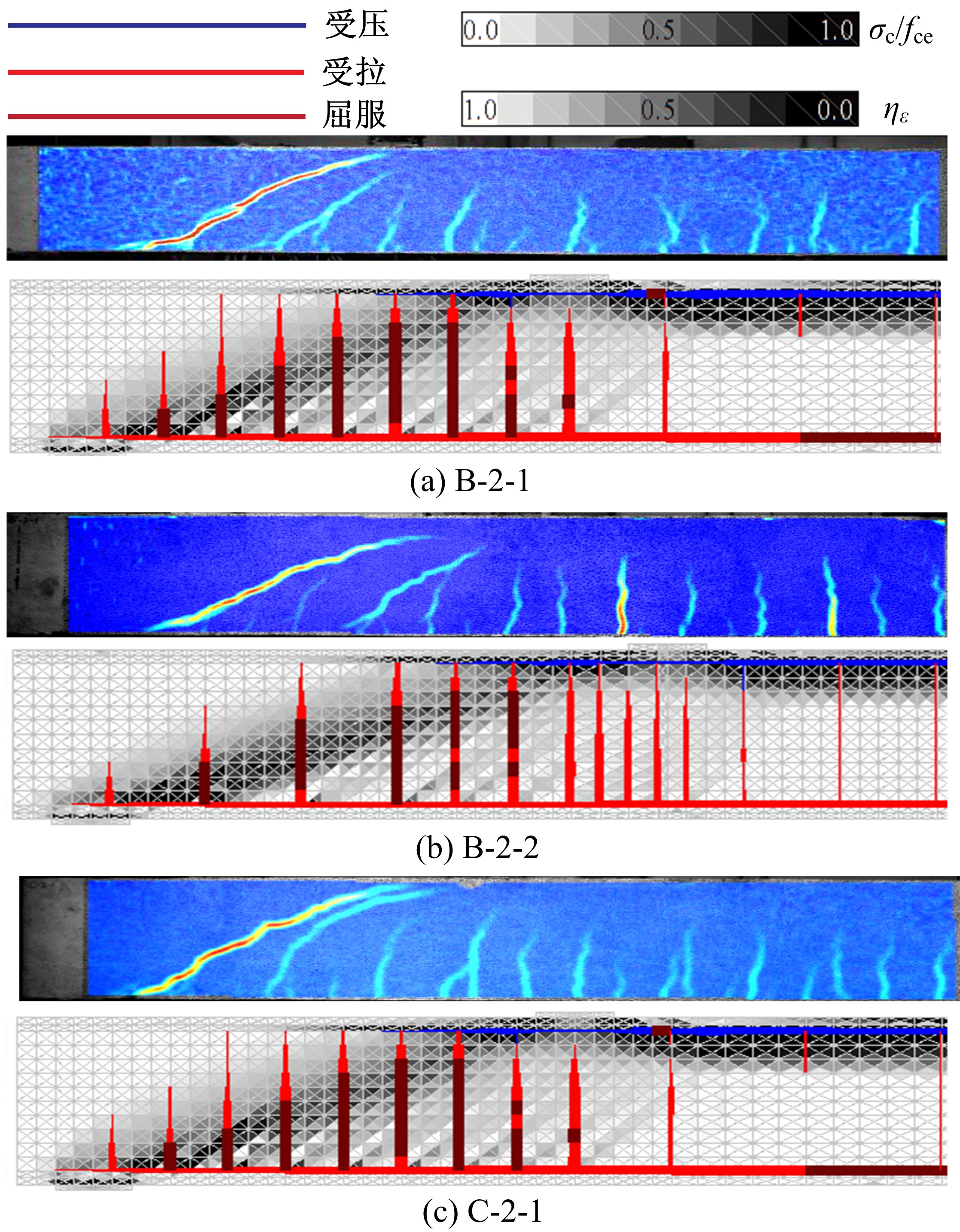
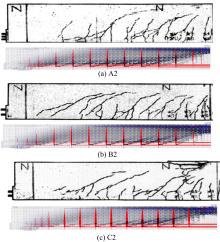
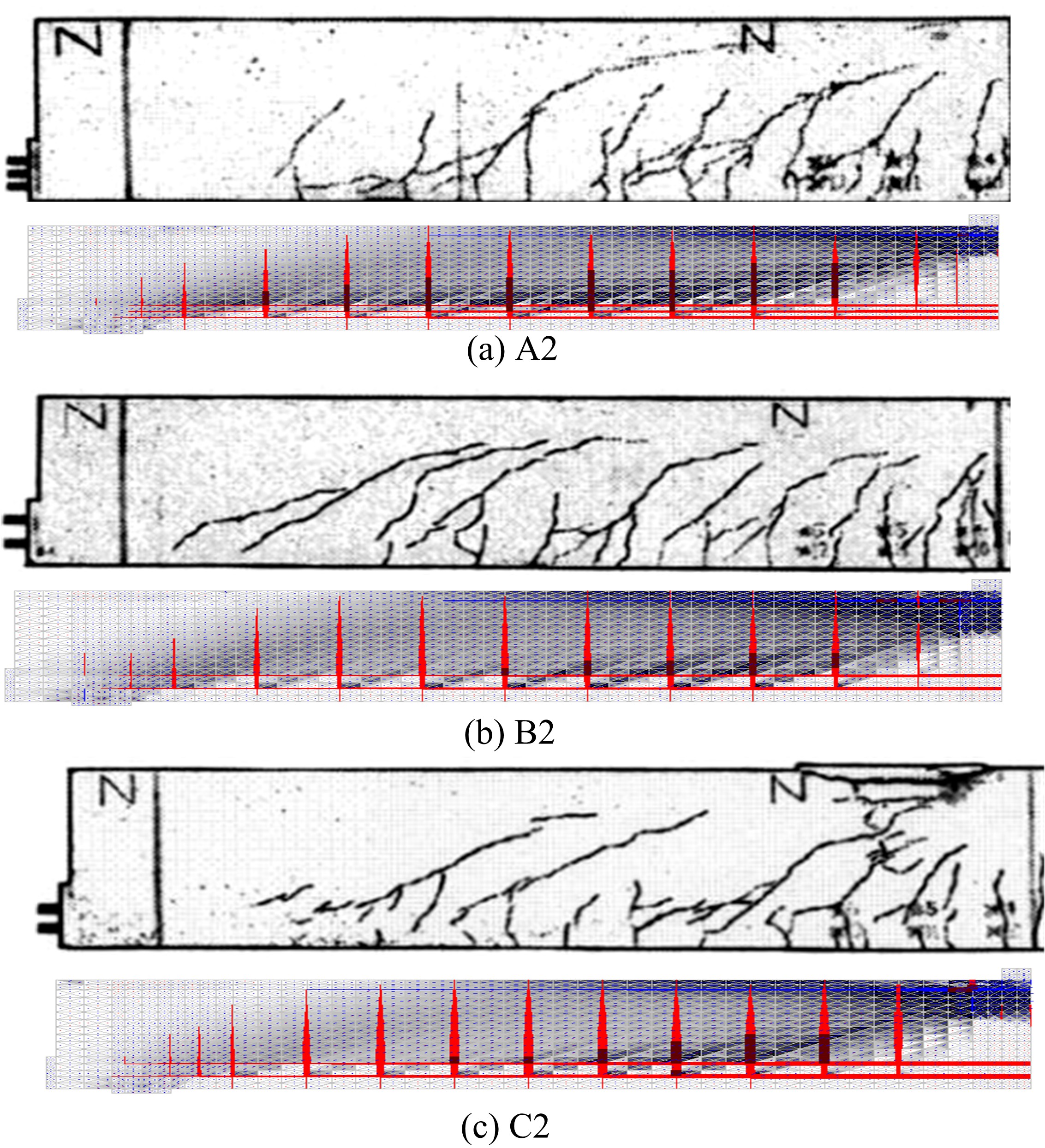
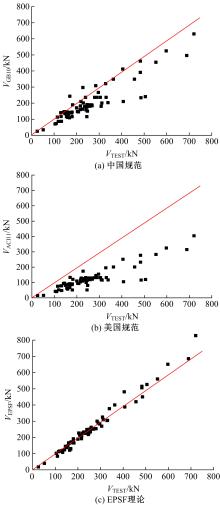
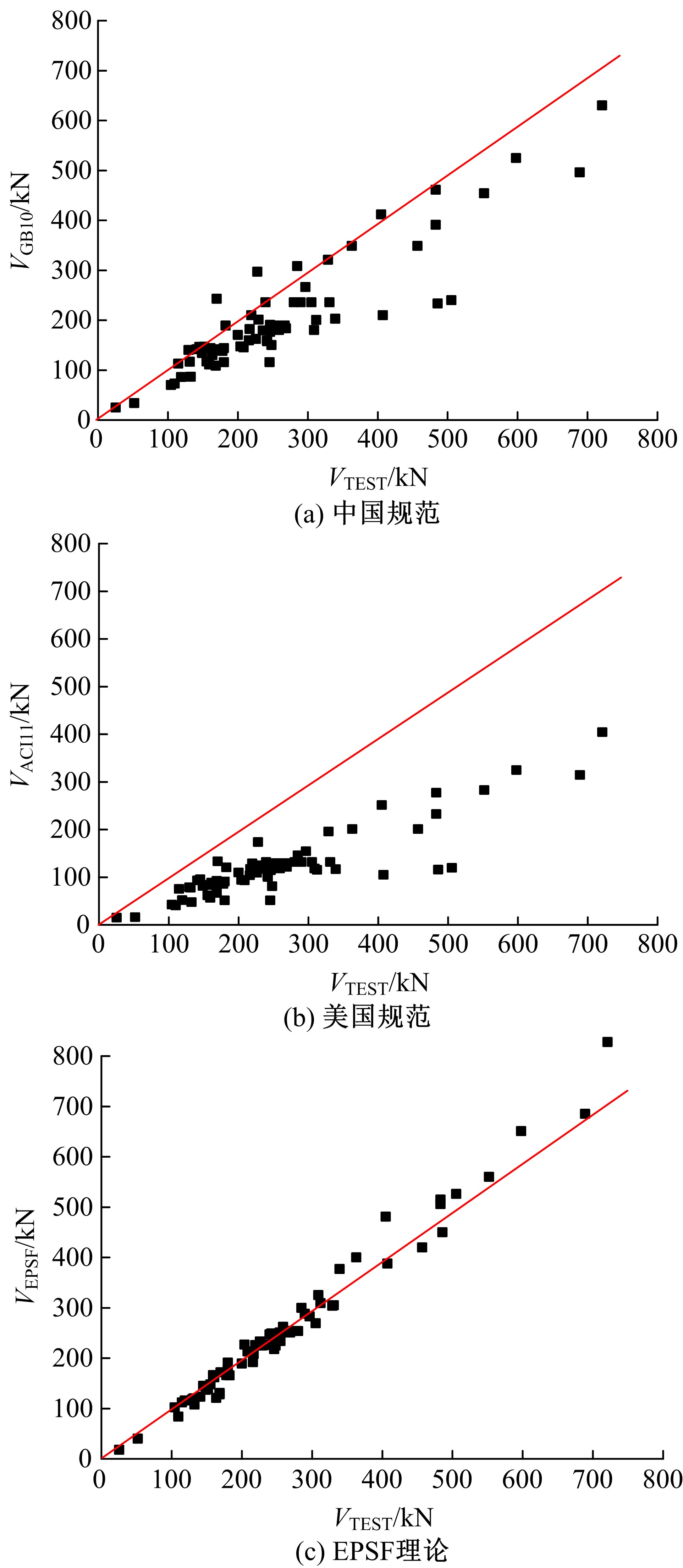
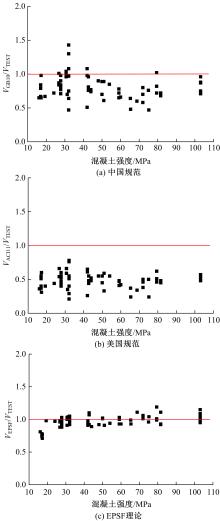
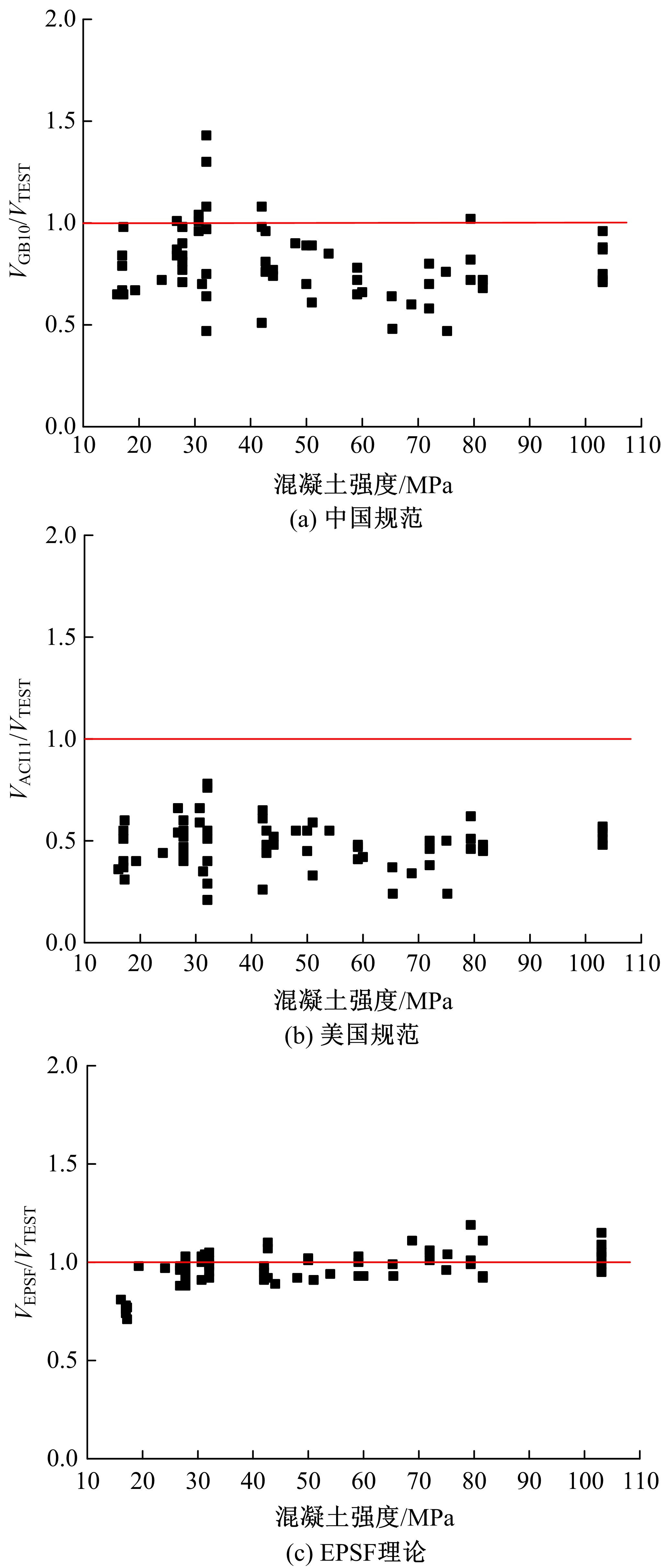
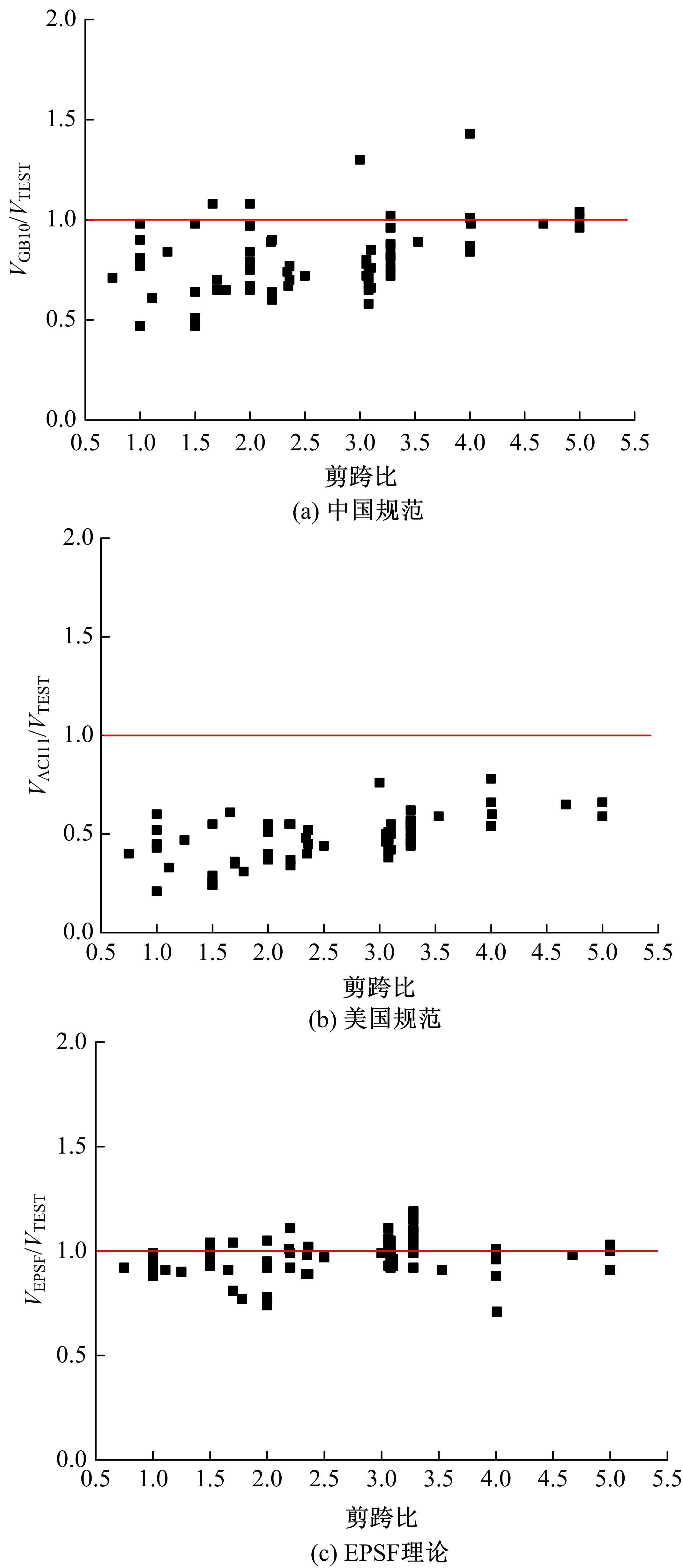
Journal of Jilin University(Engineering and Technology Edition) ›› 2021, Vol. 51 ›› Issue (1): 259-267.doi: 10.13229/j.cnki.jdxbgxb20190940
Shear strength of reinforced concrete beams based on elastoplastic stress field theory
Er-gang XIONG( ),Han XU,Ci TAN,Jing WANG,Ruo-yu DING
),Han XU,Ci TAN,Jing WANG,Ruo-yu DING
- School of Civil Engineering,Chang′an University,Xi′an 710061,China
CLC Number:
- TU375.1
| 1 | Niketić F. Development of a consistent approach for design and assessment of structural concrete members using stress fields and strut-and-tie models[D]. Lausanne: EPFL, Switzerland, 2017. |
| 2 | Ruiz M F, Muttoni A. On development of suitable stress fields for structural concrete[J]. ACI Structural Journal, 2007, 104(4): 495-502. |
| 3 | Vecchio F J, Collins M P. The modified compression-field theory for reinforced concrete elements subjected to shear[J]. ACI Structural Journal, 1986, 83(2): 219-231. |
| 4 | Muttoni A, Schwartz J, Thürlimann B. Design of Concrete Structures with Stress Fields[M]. Basel:Birkhäuser Verlag, 1997. |
| 5 | Muttoni A. Die Anwendbarkeit der Plastizitätstheorie in der Bemessung von Stahlbeton[M]. Basel:Birkhäuser Verlag, 1990. |
| 6 | CEB-FIB. Model code 2010 First final draft –Volumes 1 fib Bulletin 65[Z]. |
| 7 | Vecchio F J, Shim W. Experimental and analytical investigation of classic concrete beam tests[J]. Journal of Structural Engineering, 2004, 130(3): 460-469. |
| 8 | Frey F, Jirousek J. Méthode des éléments finis Analyse des structures et milieux continues[M]. Lausanne, Suisse: Presses Polytechnique et Universitaires Romandes, 2001. |
| 9 | 赵娜娜. 基于压力路径法钢筋混凝土梁的抗剪试验研究[D]. 西安:长安大学建筑工程学院, 2017. |
| Zhao Na-na. Behaviour of reinforced concrete beams for shear in compliance with compressive force path method[D]. Xi'an: School of Architectural Engineering, Chang'an University, 2017. | |
| 10 | ―2010. 混凝土结构设计规范[S]. |
| 11 | 阎昭琦. 基于压力路径法的大尺寸钢筋混凝土梁斜截面抗剪性能研究[D]. 西安:长安大学建筑工程学院, 2018. |
| Yan Zhao-qi. Behaviour of big size reinforced concrete beams for shear in compliance with compressive force path method[D]. Xi'an: School of Architectural Engineering, Chang'an University, 2018. | |
| 12 | 易伟建, 吕艳梅. 高强箍筋高强混凝土梁受剪试验研究[J]. 建筑结构学报, 2009, 30(4): 94-101. |
| Yi Wei-jian, Lv Yan-mei. Experimental study on shear behavior of high-strength concrete beams with high-strength stirrups[J]. Journal of Building Structures, 2009, 30(4): 94-101. | |
| 13 | 中国建筑科学研究院. 钢筋混凝土构件试验数据集——85年设计规范背景资料续编[M]. 北京:中国建筑工业出版社,1985. |
| 14 | Cladera Bohigas A. Shear design of reinforcement high-strength concrete beams[D]. Barcelona: Universitat Politècnica de Catalunya, 2002. |
| 15 | Yoon Y S, Cooc W D, Mitchell D. Minimum shear reinforcement in normal, medium and high-strength concrete beams[J]. ACI Structural Journal, 1996, 93(5): 576-584. |
| 16 | Hong S G, Kim D J, Kim S Y. Shear strength of reinforced concrete deep beams with end anchorage failure[J]. ACI Structural Journal, 2002, 99(1): 12-22. |
| 17 | 李娟. HRB500级箍筋混凝土梁斜截面受力性能试验研究[D]. 长沙:湖南大学土木工程学院,2007. |
| Li Juan. Experimental Study on mechanical behavior of diagonal section of reinforced concrete beams with HRB500 stirrups[D]. Changsha: School of Civil Engineering, Hunan University, 2007. | |
| 18 | ACI 318M―14. Building code requirements for structural concrete and commentary[S]. |
| [1] | Xue-ping FAN,Guang QU,Yue-fei LIU. Bridge extreme stress prediction based on new data assimilation algorithm [J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(2): 572-580. |
| [2] | De-lei YANG,Le-wei TONG. Calculation formula of SCF for CHS⁃CFSHS welded T⁃joints with brace under axial tension [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(6): 1891-1899. |
| [3] | SU Ying-she, YANG Yuan-yuan. Seismic compression performance of the concrete under high temperature [J]. 吉林大学学报(工学版), 2015, 45(5): 1436-1442. |
| [4] | SU Xiao-ping,WANG Qing. Corrosion damage of concrete under multi-salt soaking, freezing-thawing and dry-wet cycles [J]. 吉林大学学报(工学版), 2015, 45(1): 112-120. |
| [5] | GUO Jun-ping, DENG Zong-cai, LU Hai-bo, LIN Jin-song. Experiment on shear behavior of reinforced concrete beams strengthened with prestressed high strength steel wire mesh [J]. 吉林大学学报(工学版), 2014, 44(4): 968-977. |
| [6] | ZHANG Li-ye, GUO Xue-dong, DONG Li-juan. Bridge system mean time to failure with load-sharing process [J]. 吉林大学学报(工学版), 2013, 43(05): 1247-1252. |
| [7] | GUO Xue-dong, ZHANG Li-ye, DONG Li-juan, WU Yun-tao, ZHANG Qiang. Bridge system reliability assessment method [J]. , 2012, (03): 634-638. |
| [8] | JIANG Hao, GUO Xue-Dong, ZHANG Li-Ye. Damage diagnosis of concrete structure based on modal strain energy theory [J]. 吉林大学学报(工学版), 2010, 40(增刊): 209-0213. |
|
||