基于多球分裂的增量式k-means聚类算法

doi:10.13229/j.cnki.jdxbgxb20210098

吉林大学学报(工学版) ›› 2022, Vol. 52 ›› Issue (6): 1434-1441.doi: 10.13229/j.cnki.jdxbgxb20210098

• 计算机科学与技术 • 上一篇

基于多球分裂的增量式k-means聚类算法

曲福恒¹(),钱超越¹,杨勇^1,²(),陆洋¹,宋剑飞¹,胡雅婷³

^1.长春理工大学计算机科学技术学院，长春 130022
^2.长春师范大学教育学院，长春 130032
^3.吉林农业大学信息技术学院，长春 130118

收稿日期:2021-01-27 出版日期:2022-06-01 发布日期:2022-06-02
通讯作者: 杨勇 E-mail:qufuheng@163.com;yy@mail.ccsfu.edu.cn
作者简介:曲福恒（1979-），男，副教授，博士. 研究方向：数据挖掘和图像处理.E-mail：qufuheng@163.com
基金资助:
吉林省教育厅“十三五”科学技术项目(JJKH20181164KJ);国家自然科学基金项目(41671397);吉林省教育厅科学技术研究项目(JJKH20220330KJ)

Incremental k⁃means clustering algorithm based on multi⁃sphere splitting

Fu-heng QU¹(),Chao-yue QIAN¹,Yong YANG^1,²(),Yang LU¹,Jian-fei SONG¹,Ya-ting HU³

^1.College of Computer Science and Technology，Changchun University of Science and Technology，Changchun 130022，China
^2.College of Education，Changchun Normal University，Changchun 130032，China
^3.College of Information Technology，Jilin Agricultural University，Changchun 130118，China

Received:2021-01-27 Online:2022-06-01 Published:2022-06-02
Contact: Yong YANG E-mail:qufuheng@163.com;yy@mail.ccsfu.edu.cn

摘要/Abstract

摘要：

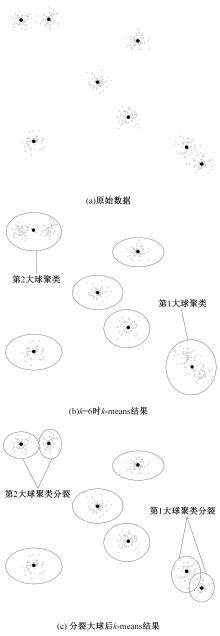
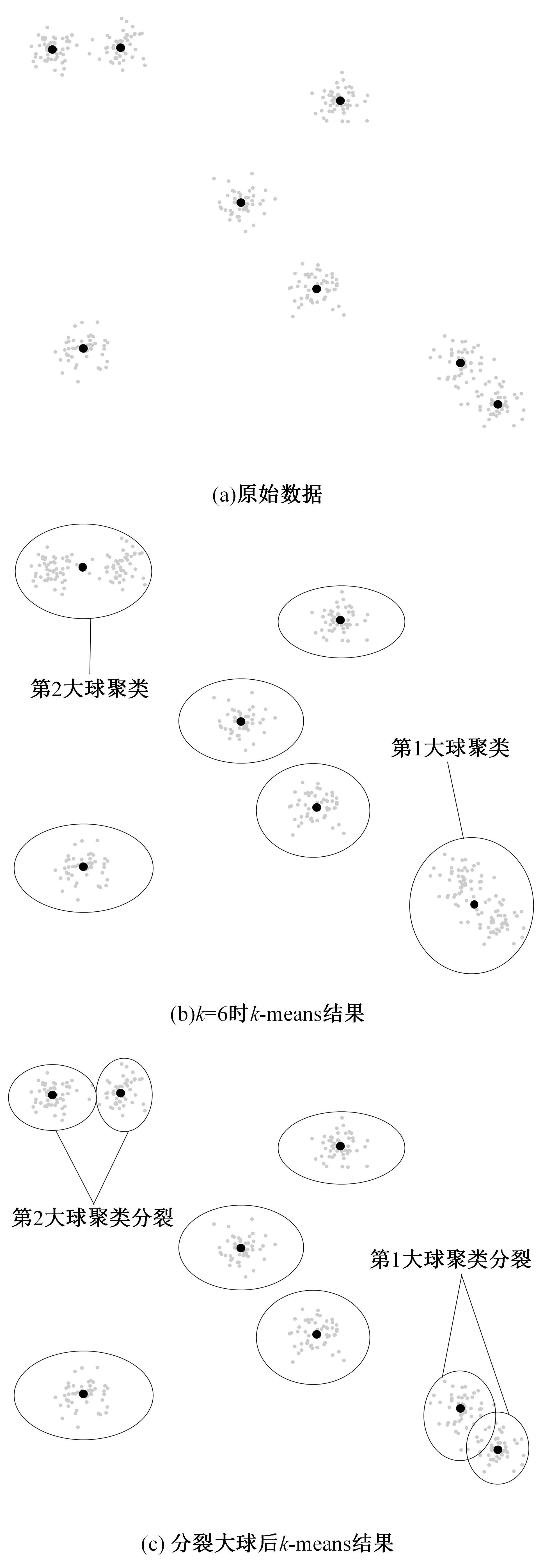
针对Ball k-means（BKM）算法对初始化中心敏感、求解精度不高的问题，提出了一种基于多球分裂的增量式k-means聚类算法。该算法利用BKM需要记录各球聚类半径的特点，从给定的初始聚类中心个数开始，按照固定步长一次性产生多个增量聚类中心，直至得到 $k$ 个初始中心。本文算法避免了所有 $n$ 个 $s$ 维数据之间的距离计算，在不增加空间复杂度的前提下将传统增量聚类中心选取的计算量由 $O (n 2 s)$ 降低至 $O k l o g k$ （k<n）。在8组UCI数据上与k-means、BKM、IK-+以及3个典型增量聚类算法的对比实验结果表明，本文算法降低了BKM的初始化敏感性，解的精度提升了37.15%~66.92%，是对比增量算法中唯一能够提升k-means效率的算法，且随着聚类个数的增加，效率优势更加明显。

关键词: 模式识别, k-means, 增量聚类, ball k-means, 多球分裂

Abstract:

To address the problem that the Ball k-means （BKM） algorithm is sensitive to the initialized centers and the solution accuracy is not high， an incremental k-means clustering algorithm based on multi-ball splitting is proposed. The algorithm takes advantage of the feature that BKM needs to record the clustering radius of each ball， starts from a given number of initial clustering centers， and generates multiple incremental clustering centers at once according to a fixed step until k initial centers are obtained. The algorithm avoids the calculation of distances between all n s-dimensional data and reduces the computation of traditional incremental clustering center selection from $O (n 2 s)$ to $O k l o g k$ （k<n） without increasing the space complexity. The experimental results of comparison with k-means， BKM， IK-+and three typical incremental clustering algorithms on 8 UCI datasets show that the proposed algorithm reduces the initialization sensitivity of BKM and improves the solution accuracy by 37.15%~66.92%； it is the only algorithm among the comparative incremental algorithms that can improve the efficiency of k-means， and the efficiency advantage becomes more obvious as the number of clusters increases.

Key words: pattern recognition, k-means, incremental clustering, ball k-means, multi-ball splitting

中图分类号:

TP391

曲福恒,钱超越,杨勇,陆洋,宋剑飞,胡雅婷. 基于多球分裂的增量式k-means聚类算法[J]. 吉林大学学报(工学版), 2022, 52(6): 1434-1441.

Fu-heng QU,Chao-yue QIAN,Yong YANG,Yang LU,Jian-fei SONG,Ya-ting HU. Incremental k⁃means clustering algorithm based on multi⁃sphere splitting[J]. Journal of Jilin University(Engineering and Technology Edition), 2022, 52(6): 1434-1441.

图/表 5

图1

表1

表2

表3

图2

参考文献 18

1	金晓民,张丽萍. 基于最小生成树的多层次k-means聚类算法及其在数据挖掘中的应用[J]. 吉林大学学报: 理学版,2018,56(5): 1187-1192.
	Jin Xiao-min, Zhang Li-ping. Multi-level k-means clustering algorithm based on minimum spanning tree and its application in data mining[J]. Journal of Jilin University(Science Edition),2018, 56(5): 1187-1192.
2	张杰,卓灵,朱韵攸. 一种k-means聚类算法的改进与应用[J]. 电子技术应用,2015,41(1): 125-128, 131.
	Zhang Jie, Zhuo Ling, Zhu Yun-xiao. Improvement and application of a k-means clustering algorithm[J]. Application of Electronic Technology, 2015, 41(1): 125-128, 131.
3	刘仲民,李战明,李博皓,等. 基于稀疏矩阵的谱聚类图像分割算法[J]. 吉林大学学报: 工学版,2017,47(4): 1308-1313.
	Liu Zhong-min, Li Zhan-ming, Li Bo-hao, et al. Spectral clustering image segmentation based on sparse matrix[J]. Journal of Jilin University(Engineering and Technology Edition), 2017, 47(4): 1308-1313.
4	Elkan C. Using the triangle inequality to accelerate k-means[C]∥Proceedings of the 20th International Conference on Machine Learning,La Jolla, California, 2003: 147-153.
5	Hamerly G. Making k-means even faster[C]∥Proceedings of the 2010 SIAM International Conference on Data Mining, Columbus, Ohio, USA, 2010: 130-140.
6	Drake J, Hamerly G. Accelerated k-means with adaptive distance bounds[C]∥5th NIPS Workshop on Optimization for Machine Learning, Lake Tahoe, California, America, 2012.
7	Newling J, Fleuret F. Fast k-means with accurate bounds[C]∥ICML'16: Proceedings of the 33rd International Conference on International Conference on Machine Learning, New York, America, 2016: 936-944.
8	Ding Y F, Zhao Y, Shen X P, et al. Yinyang k-means: a drop-in replacement of the classic k-means with consistent speedup[C]∥Proceedings of the 32nd International Conference on Machine Learning, Lila, France, 2015: 579-587.
9	Xia S Y, Peng D W, Meng D Y, et al. Ball k-means: fast adaptive clustering with no bounds[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022, 44(1): 87-99.
10	Likas A, Vlassis N, Verbeek J J. The global k-means clustering algorithm[J]. Pattern Recognition, 2003, 36(2): 451-461.
11	Bagirov A M. Modified global k-means algorithm for minimum sum-of-squares clustering problems[J]. Pattern Recognition, 2008, 41(10): 3192-3199.
12	Bagirov A M, Ugon J, Webb D. Fast modified global k-means algorithm for incremental cluster construction[J]. Pattern Recognition, 2011, 44(4): 866-876.
13	Ordin B, Bagirov A M. A heuristic algorithm for solving the minimum sum-of-squares clustering problems[J]. Journal of Global Optimization, 2015, 61(2): 341-361.
14	Xie J, Jiang S, Xie W, et al. An efficient global k-means clustering algorithm[J]. Journal of Computers, 2011, 6(2): 271-279.
15	Yang X, Li Y, Sun Y, et al. Fast and robust rbf neural network based on global k-means clustering with adaptive selection radius for sound source angle estimation[J]. IEEE Transactions on Antennas and Propagation, 2018, 66(6): 3097-3107.
16	于剑,程乾生. 模糊聚类方法中的最佳聚类数的搜索范围[J]. 中国科学,2002,32(2): 275-280.
	Yu Jian, Cheng Qian-sheng. The search range of optimal cluster number in fuzzy clustering method[J]. China Science, 2002, 32(2): 275-280.
17	Hartigan J A, Wong M A. Algorithm AS 136: a k-means clustering algorithm[J]. Applied Statistics, 1979, 28(1): 100-108.
18	Ismkhan H. Ik-means-+: an iterative clustering algorithm based on an enhanced version of the k-means[J]. Pattern Recognition, 2018, 79: 402-413.

相关文章 15

[1]	徐卓君,杨雯婷,杨承志,田彦涛,王晓军. 雷达脉内调制识别的改进残差神经网络算法[J]. 吉林大学学报(工学版), 2021, 51(4): 1454-1460.
[2]	袁哲明,袁鸿杰,言雨璇,李钎,刘双清,谭泗桥. 基于深度学习的轻量化田间昆虫识别及分类模型[J]. 吉林大学学报(工学版), 2021, 51(3): 1131-1139.
[3]	刘富,刘璐,侯涛,刘云. 基于优化MSR的夜间道路图像增强方法[J]. 吉林大学学报(工学版), 2021, 51(1): 323-330.
[4]	翟凤文,党建武,王阳萍,金静,罗维薇. 基于扩展轮廓的快速仿射不变特征提取[J]. 吉林大学学报(工学版), 2019, 49(4): 1345-1356.
[5]	刘富, 兰旭腾, 侯涛, 康冰, 刘云, 林彩霞. 基于优化k-mer频率的宏基因组聚类方法[J]. 吉林大学学报(工学版), 2018, 48(5): 1593-1599.
[6]	顾播宇,孙俊喜,李洪祚,刘红喜,刘广文. 基于特征加权模块双方向二维主成分分析的人脸识别[J]. 吉林大学学报(工学版), 2014, 44(3): 828-833.
[7]	常志勇, 陈东辉, 张凌, 佟月英, 翁小辉, 佟金. 基于多传感器融合的鸡肉新鲜度检测方法[J]. 吉林大学学报(工学版), 2013, 43(增刊1): 493-496.
[8]	陈万忠, 孙保峰, 高韧杰, 雷俊. 基于NNE技术的手臂运动模式识别算法研究[J]. 吉林大学学报(工学版), 2013, 43(增刊1): 69-73.
[9]	李阳, 田彦涛, 陈万忠. 基于半监督boosting表面肌电信号多类模式识别[J]. 吉林大学学报(工学版), 2013, 43(05): 1415-1426.
[10]	杨冬风, 马秀莲. 基于分形纹理分析的蛋壳裂纹识别[J]. 吉林大学学报(工学版), 2011, 41(增刊1): 348-352.
[11]	王丹, 张祥合, 张立, 任露泉. 多维多分辨仿生识别方法及其应用[J]. 吉林大学学报(工学版), 2011, 41(02): 408-0412.
[12]	王利民,臧雪柏,曹春红2. 基于广义信息论的决策森林数据挖掘模型[J]. 吉林大学学报(工学版), 2010, 40(01): 155-0158.
[13]	王旭，陈永刚，杨印生 . 含有区间数的DEA-DA模型及灵敏度[J]. 吉林大学学报(工学版), 2009, 39(03): 716-0720.
[14]	李伦波，马广富 . 基于RBPNN的退化交通标志图像的识别算法[J]. 吉林大学学报(工学版), 2008, 38(06): 1429-1433.
[15]	谭梅，尹义龙，杨卫辉. 基于区域水平的指纹纹线距离估计方法[J]. 吉林大学学报(工学版), 2005, 35(05): 537-0541.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

数据集	数据个数	数据维数
iris	150	4
wine	178	13
Breast Cancer （BC）	569	30
Wine Quality （WQ）	4 898	12
Abalone	4 177	8
Page block	5 473	10
Condition Based Maintenance （CO）	11 934	16
EEG Eye State（EE）	14 980	14

k	数据集	BKM	FGKM（E）	IK-+（E）	MS-MGKM（E）	本文（E）
10	iris	30.14	11.38	12.47	14.33	8.17
	wine	3.89×10⁵	43.45	40.78	43.49	24.85
	BC	1.02×10⁷	14.54	4.57	17.55	0.67
	WQ	1.07×10⁶	2.29	1.80	3.10	-2.48
	Abalone	2.57×10³	26.55	27.16	33.10	6.05
	Page block	1.43×10¹⁰	67.89	67.42	68.14	61.46
	CO	1.16×10¹¹	98.98	98.82	98.97	98.53
	EE	3.37×10¹¹	99.99	99.99	99.99	99.97
	平均值		45.63	44.13	47.33	37.15
20	iris	18.12	17.17	15.93	20.87	9.66
	wine	1.57×10⁵	54.45	51.64	56.16	46.24
	BC	8.16×10⁶	55.01	56.00	58.02	52.28
	WQ	6.33×10⁵	7.05	6.61	8.67	3.82
	Abalone	1.33×10³	49.43	48.37	51.59	32.55
	Page block	1.34×10¹⁰	87.25	85.45	87.29	81.54
	CO	1.96×10¹⁰	99.58	99.56	99.58	99.38
	EE	3.37×10¹¹	99.99	99.99	99.99	99.99
	平均值		58.74	57.94	60.27	53.18
50	WQ	3.47×10⁵	19.13	17.81	20.42	13.32
	Abalone	476.69	66.86	66.00	67.64	59.51
	Page block	1.31×10¹⁰	96.72	93.62	96.76	92.30
	CO	9.29×10⁷	76.51	75.57	76.44	69.49
	EE	3.13×10¹¹	99.99	99.99	99.99	99.99
	平均值		71.84	70.60	72.25	66.92

k	数据集	KM/ms	FGKM（I）	IK-+（I）	MS-MGKM（I）	BKM（I）	FGBKM（I）	本文（I）
10	BC	7.18	-1 085.93	-17.83	-9 326.18	69.64	-1 074.37	79.80
	WQ	41.24	-6 346.65	-34.29	-101 722.50	47.67	-6 443.31	33.45
	Abalone	8.72	-13 585.78	-21.10	-38 195.87	39.22	-14 061.93	35.62
	Page block	53.64	-6 522.30	63.53	-15 357.49	18.49	-6 735.46	66.63
	CO	33.76	-46 953.32	-45.56	-94 534.68	62.91	-48 530.63	21.56
	EE	176.86	-14 315.02	-55.94	-2 798.45	-12.97	-14 563.35	-66.37
	平均值		-14 801.50	-18.53	-43 655.86	37.49	-15 234.84	28.45
20	BC	8.72	-1 924.08	-42.89	-16 188.99	85.55	-1 849.31	71.64
	WQ	90.64	-5 780.41	-67.92	-69 578.51	70.37	-5 769.33	66.26
	Abalone	20.58	-12 317.88	-22.45	-48 183.77	72.69	-12 559.48	59.03
	Page block	316.32	-2 204.25	83.83	-9 885.65	69.34	-2 271.93	86.71
	CO	101.48	-33 320.77	-128.58	-44 973.71	83.64	-33 805.20	70.20
	EE	608.42	-8 757.01	-73.31	-2 294.40	47.58	-8 800.83	54.12
	平均值		-10 717.40	-41.89	-31 850.84	71.53	-10 842.68	67.99
50	WQ	141.62	-9 313.36	-177.39	-77 101.10	84.56	-9 011.35	76.63
	Abalone	84.98	-7 819.04	-7.63	-39 362.23	89.74	-7 803.91	82.39
	Page block	864.60	-1 951.95	74.88	-7 893.41	85.03	-1 972.65	89.60
	CO	380.10	-23 082.16	-142.18	-19 747.88	93.43	-23 085.37	85.11
	EE	1469.48	-9 462.43	-58.02	-3 079.38	65.85	-9 267.26	75.45
	平均值		-10 391.06	-62.07	-29 436.80	81.69	-10 330.54	79.53

基于多球分裂的增量式k-means聚类算法

Incremental k⁃means clustering algorithm based on multi⁃sphere splitting

RICH HTML

PDF (PC)

摘要/Abstract

引用本文

使用本文

图/表 5

参考文献 18

相关文章 15

Metrics

本文评价

推荐阅读 0