螺栓结合面法向接触刚度不确定性量化

doi:10.13229/j.cnki.jdxbgxb.20211023

摘要/Abstract

摘要：

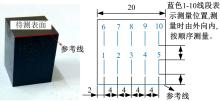
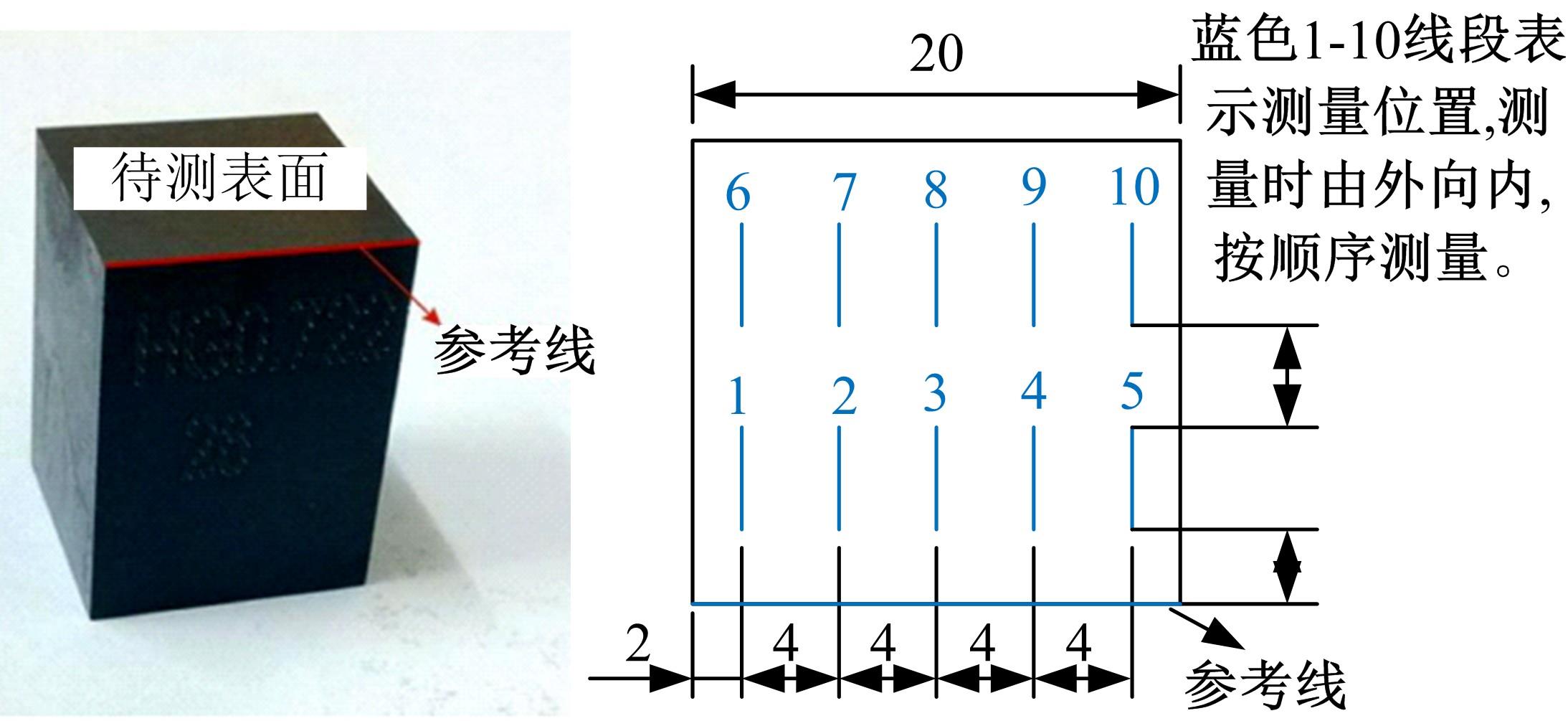
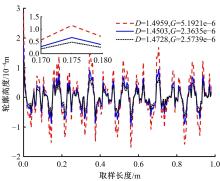
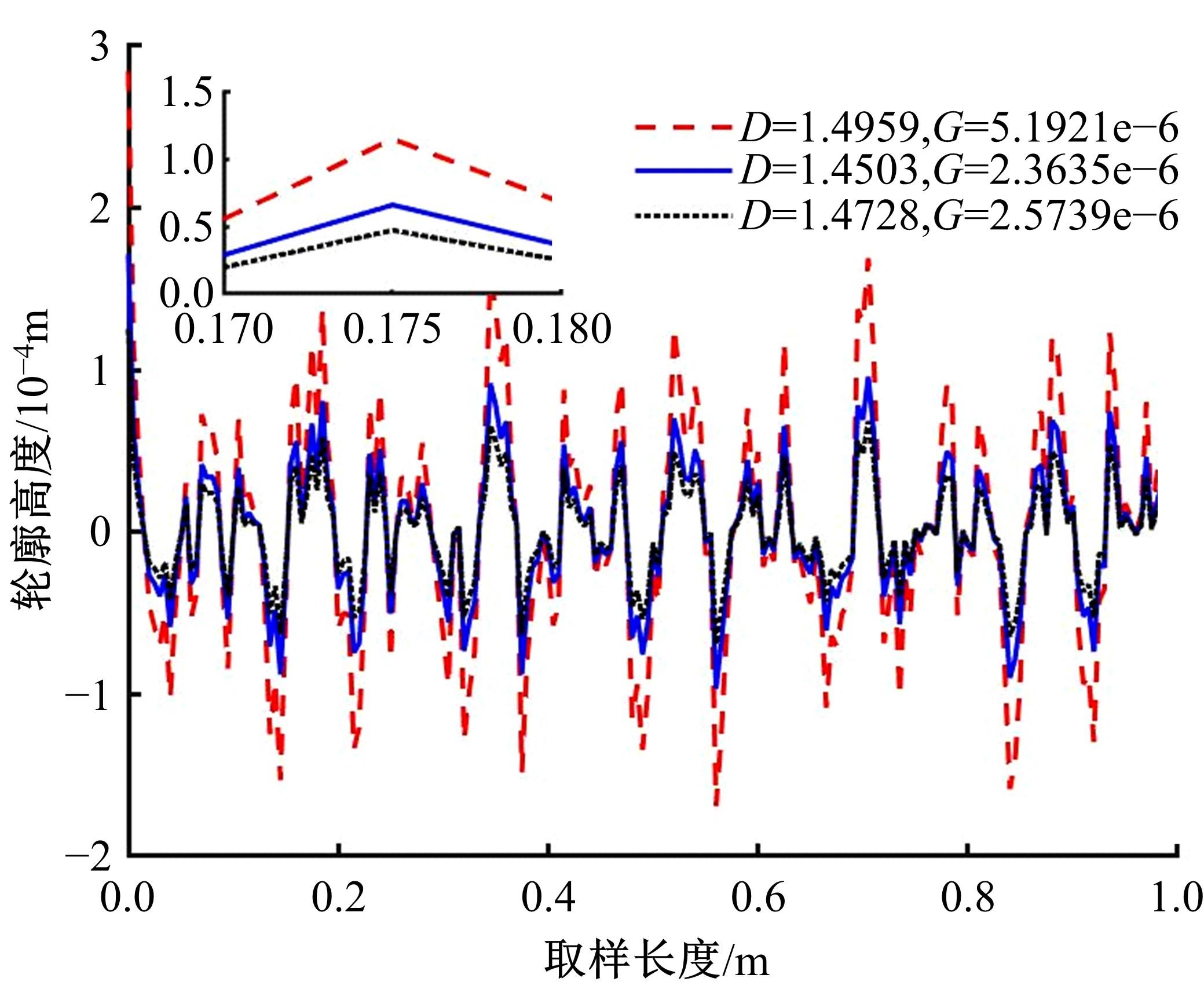
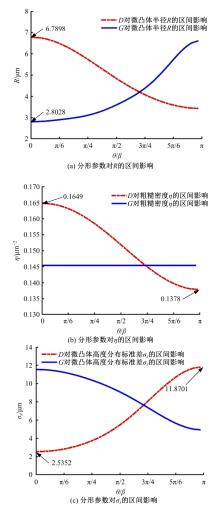
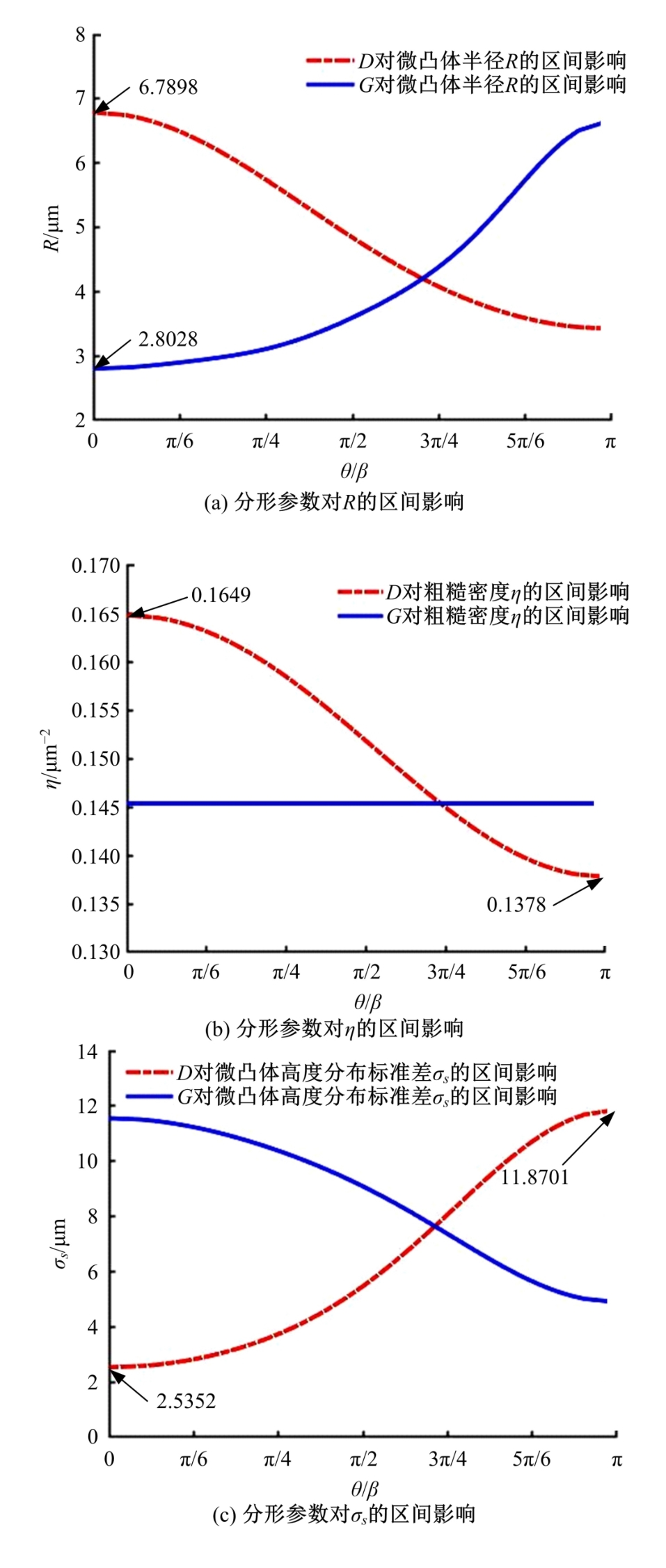
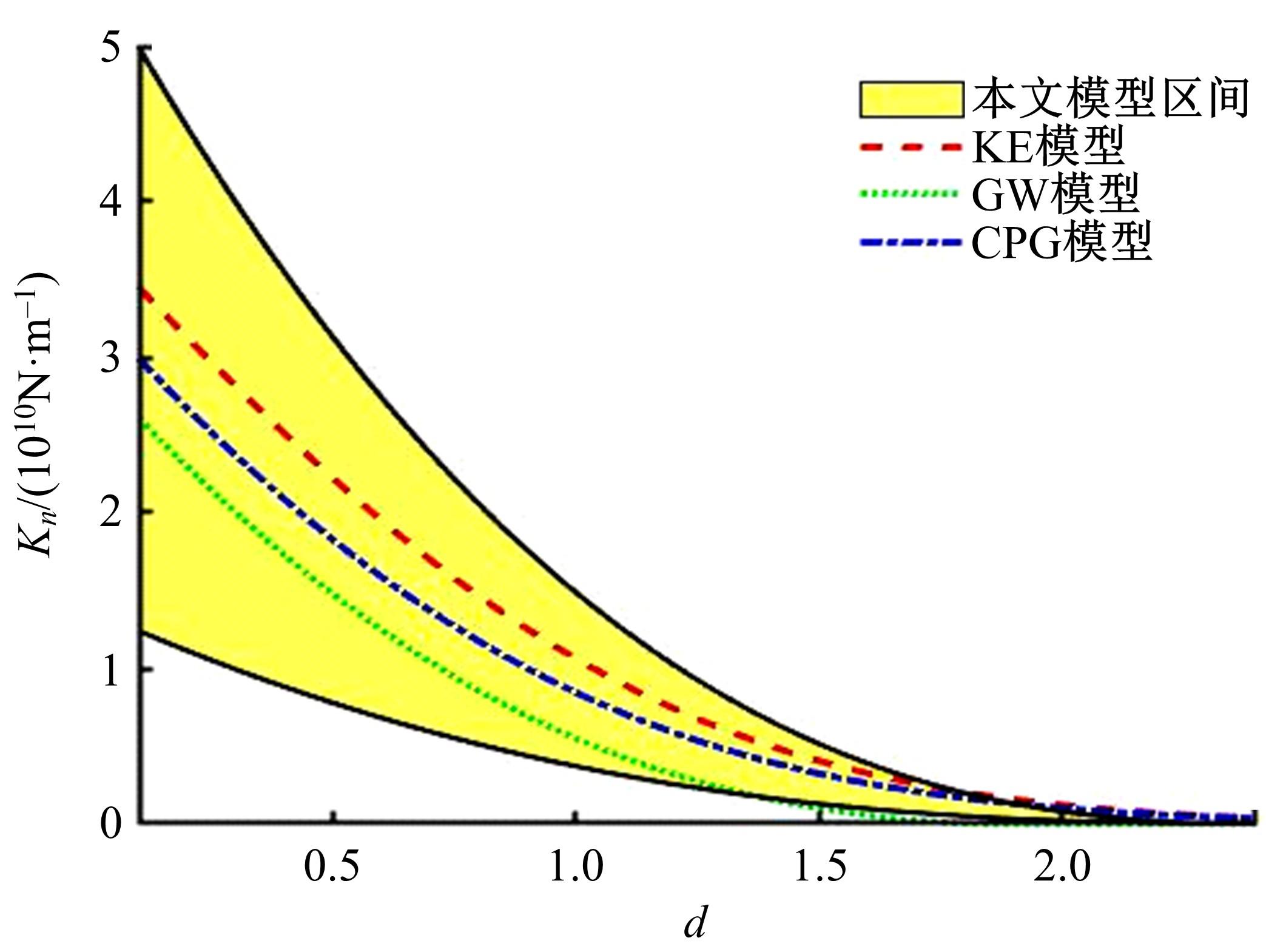
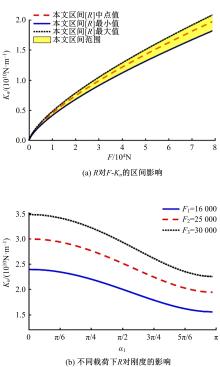
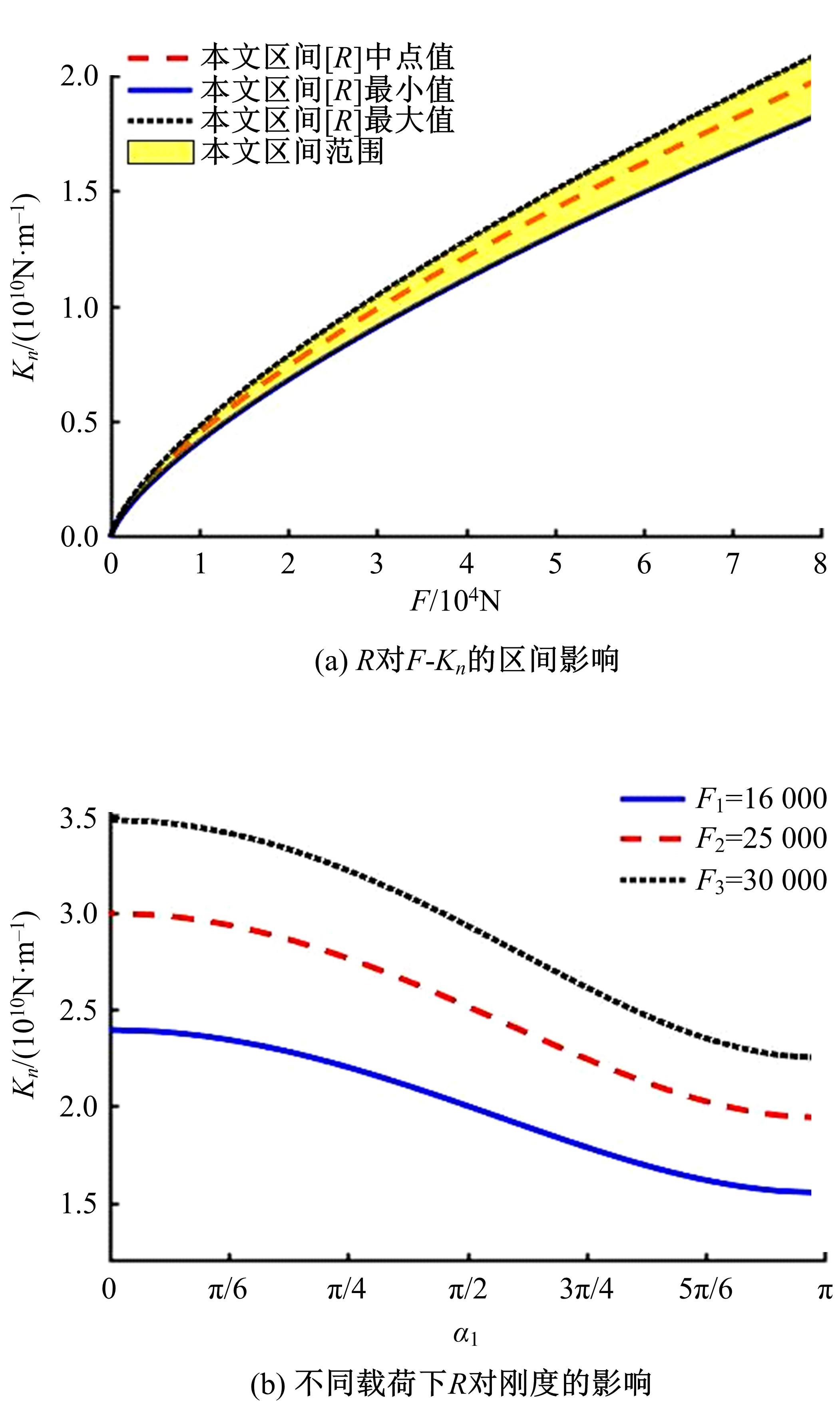
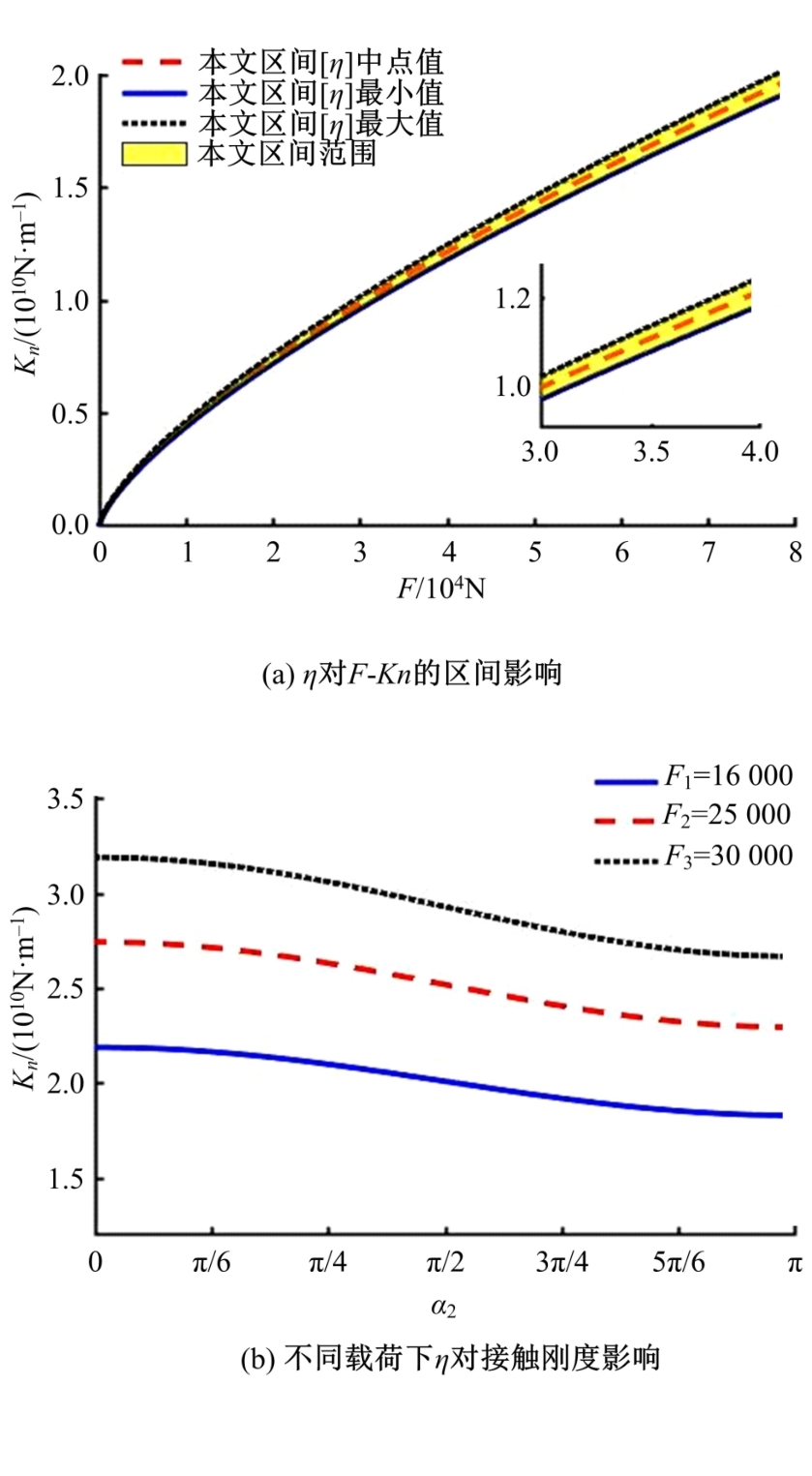
螺栓结合面接触中存在诸多不确定性因素，现有模型难以确定接触刚度的合理区间，为此，应用区间估计理论以获得微观形貌不确定的结合面接触刚度变化范围。首先，基于分形理论表征结合面微凸体轮廓高度，采用结构函数法和区间算法求解结合面分形参数不确定性区间；然后，通过矩谱法将表面形貌参数与分形参数并联，并引入切比雪夫包络函数计算出不确定性因素影响下的表面形貌参数区间；最后，将形貌参数不确定区间引入统计模型，建立考虑表面形貌参数不确定的结合面接触刚度模型，获得结合面接触刚度的区间，并探究了表面形貌参数对结合面接触刚度的影响。结果表明：该模型能准确预测螺栓结合面接触刚度的变化范围，可为结合面的设计提供指导。

关键词: 摩擦力学, 不确定性, 结合面, 接触刚度, 表面形貌参数, 切比雪夫包络函数

Abstract:

There are many uncertainties in the contact of bolted joints. It is difficult to determine the reasonable interval of contact stiffness in existing models. Therefore， the range of contact stiffness of joint surface with uncertain micromorphology is obtained by using interval Estimation theory. Firstly， based on fractal theory to characterize the contour height of the micro-convex body of the combined surface， the structural function method and interval algorithm are used to solve the uncertainty interval of the fractal parameters of the combined surface. Then， the surface topography parameters are connected in parallel with the fractal parameters by moment spectroscopy. The Chebyshev envelope function is introduced to calculate the surface morphology parameters interval under the influence of uncertainty. Finally， the uncertainty interval of surface morphology parameters is introduced into the statistical model to establish the contact stiffness model of joint surface considering the uncertainty of surface morphology parameters. The range of joint surface contact stiffness is obtained， and the influence of surface morphology parameters on the joint surface contact stiffness is explored. The results indicate that the model can accurately predict the range of changes in the surface contact stiffness of bolted connections， which can provide guidance for the design of the joint surface.

Key words: friction mechanics, uncertainty, joint surface, contact stiffness, surface topography parameters, Chebyshev envelope function

中图分类号:

TH131.3

李玲,赵凯,林红,王晶晶,蔡安江. 螺栓结合面法向接触刚度不确定性量化[J]. 吉林大学学报(工学版), 2023, 53(7): 1911-1919.

Ling LI,Kai ZHAO,Hong LIN,Jing-jing WANG,An-jiang CAI. Uncertainty quantification of normal contact stiffness of bolt joint surface[J]. Journal of Jilin University(Engineering and Technology Edition), 2023, 53(7): 1911-1919.

图/表 9

图1

表1

图2

图3

表2

图4

图5

图6

图7

参考文献 21

1	Burdekin M, Back N, Cowley A. Analysis of the local-deformations in machine joints[J]. ARCHIVE Journal of Mechanical Engineering Science, 1979, 21(1): 25-32.
2	杨成, 赵永胜, 刘志峰, 等.基于多尺度理论的栓接结合部动力学建模[J]. 吉林大学学报:工学版, 2019, 49(4): 1212-1220.
	Yang Cheng, Zhao Yong-sheng, Liu Zhi-feng, et al. Stiffness model of bolted joint based on multi-scale theory[J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(4): 1212-1220.
3	廖静平, 张建富, 郁鼎文, 等. 基于虚拟梯度材料的螺栓结合面建模方法[J]. 吉林大学学报:工学版, 2016, 46(4): 1149-1155.
	Liao Jing-ping, Zhang Jian-fu, Yu Ding-wen, et al. Modeling method of bolted joint interface based on gradient virtual materials[J]. Journal of Jilin University (Engineering and Technology Edition), 2016, 46(4): 1149-1155.
4	Ahmadian H, Mohsen M. A distributed mechanical joint contact model with slip/slap coupling effects[J]. Mechanical Systems and Signal Processing, 2016, 80: 206-223.
5	Brake M. The Mechanics of Jointed Structures: Recent Research and Open Challenges for Developing Predictive Models for Structural Dynamics[M]. Switzerland: Springer Nature, 2018.
6	Greenwood J A, Williamson J B P. Contact of nominally flat surfaces[J]. Proceedings of the Royal Society of London, 1966, 295(1442): 300-319.
7	Chang W R, Etsion I, Bogy D B. An elastic-plastic model for the contact of rough surfaces[J]. Asme J Trib, 1987, 109(2): 257-263.
8	Ciavarella M, Greenwood J A, Paggi M. Inclusion of "interaction" in the Greenwood and Williamson contact theory[J]. Wear, 2008, 265(5/6): 729-734.
9	Li Ling, Wang Jing⁃jing, Pei Xi⁃yong, et al. A modified elastic contact stiffness model considering the deformation of bulk substrate[J]. Journal of Mechanical Science and Technology, 2020, 34(10): 777-790.
10	Sayles R S, Thomas T R. Surface topography as a nonstationary random process[J]. Nature, 1978, 271(5644): 431-434.
11	Wang S, Komvopoulos K. A fractal theory of the interfacial temperature distribution in the slow sliding regime: part I—elastic contact and heat transfer analysis[J]. Journal of Tribology, 1994, 116(4): 812-822.
12	Wang S, Komvopoulos K. A fractal theory of the interfacial temperature distribution in the slow sliding regime: part II—multiple domains[J]. Journal of Tribology, 1994, 116(4): 824-832.
13	Yan W, Komvopoulos K. Contact analysis of elastic-plastic fractal surfaces[J]. Journal of Applied Physics, 1998, 84(7): 3617-3624.
14	Zhao Yong-sheng, Wu Hong-chao, Yang Cong-bin, et al. Interval estimation for contact stiffnes-s of bolted joint with uncertain parameters[J]. Advances in Mechanical Engineering, 2019, 11(11): 1-16.
15	Seibel A, Japing A, Schlattmann J. Uncertainty analysis of the coefficients of friction during the tightening process of bolted joints[J]. Journal of Uncertainty Analysis & Applications, 2014, 2(1): 1-11.
16	Langer P, Sepahvand K, Guist C, etal. Finite element modeling for structural dynamic analysis of bolted joints under uncertainty[J]. Procedia Engineering, 2017, 199: 954-959.
17	Dohnal F, Mace B R, Ferguson N S. Joint uncertainty propagation in linear structural dynamics using stochastic reduced basis methods[J]. AIAA Journal, 2009, 47(4): 961-969.
18	李坤, 曾劲, 于明月, 等. 考虑螺栓连接刚度不确定性的带法兰-圆柱壳结构频响函数分析[J]. 振动工程学报, 2020(3): 517-524.
	Li Kun, Zeng Jin, Yu Ming-yue, et al. Analysis of frequency response function of flanged-cylinder shell structure considering the uncertainty of bolt connection stiffness[J]. Chinese Journal of Vibration Engineering, 2020(3): 517-524.
19	Li Hong-shuang, Gu Ru⁃jia, Zhao Xiang. Global sensitivity analysis of load distribution and displacement in multi-bolt composite joints. Composites[J]. Composites Part B, 2017, 116:200-210.
20	Majumdar A, Bhushan B. Fractal model of elastic-plastic contact between rough surfaces[J]. Tribol Trans ASME, 1991, 113(1): 1-11.
21	Xiao H, Sun Y. On the normal contact stiffness and contact resonance frequency of rough surface contact based on asperity micro-contact statistical models[J]. European Journal of Mechanics-A/Solids, 2019, 75: 450-460.

相关文章 15

[1]	龙海波,杨家其,尹靓,赵学彧,向子权. 基于鲁棒优化的不确定需求下应急物资配送多目标决策模型[J]. 吉林大学学报(工学版), 2023, 53(4): 1078-1084.
[2]	程功,肖科,王家序,蒲伟,韩彦峰. 混合润滑状态下齿轮接触刚度[J]. 吉林大学学报(工学版), 2020, 50(2): 494-503.
[3]	江海宇, 刘玉海, 孙海林, 徐克彬, 白田增, 陈祖斌. 微地震地面监测层状起伏速度模型校正算法[J]. 吉林大学学报(工学版), 2017, 47(6): 1969-1975.
[4]	冯建鑫. 具有测量时滞的不确定系统的递推鲁棒滤波[J]. 吉林大学学报(工学版), 2017, 47(5): 1561-1567.
[5]	廖静平, 张建富, 郁鼎文, 冯平法. 基于虚拟梯度材料的螺栓结合面建模方法[J]. 吉林大学学报(工学版), 2016, 46(4): 1149-1155.
[6]	郭学东, 马立军, 张云龙. 集中力作用下考虑剪切滑移效应的双层结合面组合梁解析解[J]. 吉林大学学报(工学版), 2016, 46(2): 432-438.
[7]	冯建鑫, 王挺峰, 郭劲. 测量丢失不确定性系统的迭代鲁棒滤波[J]. 吉林大学学报(工学版), 2014, 44(4): 1057-1061.
[8]	富爽,李一兵,叶方,高振国. 利用频域Sevcik分形维数进行快速盲频谱感知[J]. 吉林大学学报(工学版), 2014, 44(3): 854-860.
[9]	李静, 胡云安, 温玮. 非周期时变非线性系统自适应迭代学习控制 [J]. , 2012, (03): 702-708.
[10]	杨志晓, 范艳峰, 孙福艳. 基于正态云模型的虚拟人点头动作不确定性控制[J]. 吉林大学学报(工学版), 2012, 42(02): 476-482.
[11]	矫德余. 四轮驱动车鲁棒轨迹跟踪控制器设计[J]. 吉林大学学报(工学版), 2011, 41(增刊2): 301-305.
[12]	邵继业,王日新,徐敏强. 贝叶斯网络在模型诊断中的应用[J]. 吉林大学学报(工学版), 2010, 40(01): 234-0237.
[13]	吕灵灵, 段广仁, 吴爱国. 滞后细胞神经网络的鲁棒无源分析[J]. 吉林大学学报(工学版), 2009, 39(04): 1007-1011.
[14]	王小兵,陈建军,陈永琴,谢永强,陈龙 . 小区间参数不确定热机电耦合智能薄板的鲁棒控制[J]. 吉林大学学报(工学版), 2009, 39(01): 182-187.
[15]	刘序宗，刘树彬，郑伟，安琪 . BESⅢ TOF子触发系统击中信息多通道串行同步传输方法[J]. 吉林大学学报(工学版), 2008, 38(02): 483-0488.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

实验次数	D	G/10^-7mm
1	1.3908	6.6440
2	1.3971	8.5597
3	1.3921	9.1981
4	1.4503	23.635
5	1.4728	25.739
6	1.3917	6.9936
7	1.4525	8.9967
8	1.4635	40.223
9	1.5070	30.278
10	1.4959	51.1981

	区间	区间半径	区间中点
［R］/μm	［2.8028， 6.7898］	2.0533	4.7963
［η］/μm ^-²	［0.1378， 0.1649］	0.01391	0.1514
［σ_s ］/μm	［2.5352， 11.8701］	4.8075	7.2027