吉林大学学报(工学版) ›› 2024, Vol. 54 ›› Issue (3): 711-718.doi: 10.13229/j.cnki.jdxbgxb.20220551
• 交通运输工程·土木工程 • 上一篇
城市群轨道交通直通线路优化设置方法
- 吉林大学 交通学院,长春 130022
Optimal setting method of rail transit through lines in urban agglomeration
Wen-jing WU( ),Kang-bei XIONG,Hong-fei JIA(
),Kang-bei XIONG,Hong-fei JIA( ),Qing-yu LUO
),Qing-yu LUO
- College of Transportation,Jilin University,Changchun 130022,China
摘要:
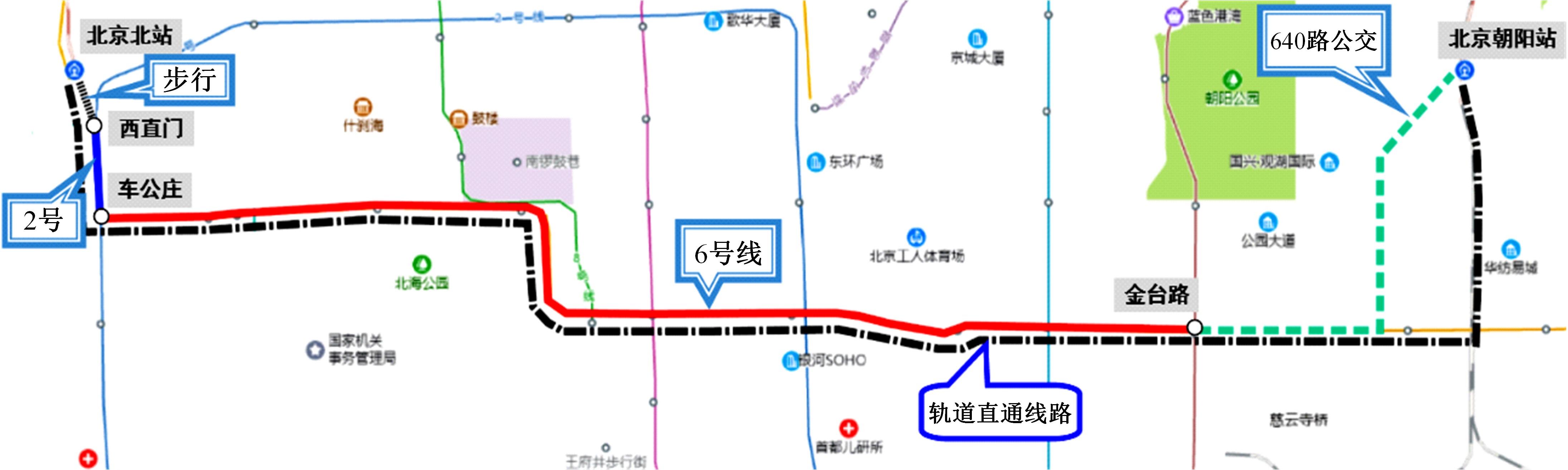
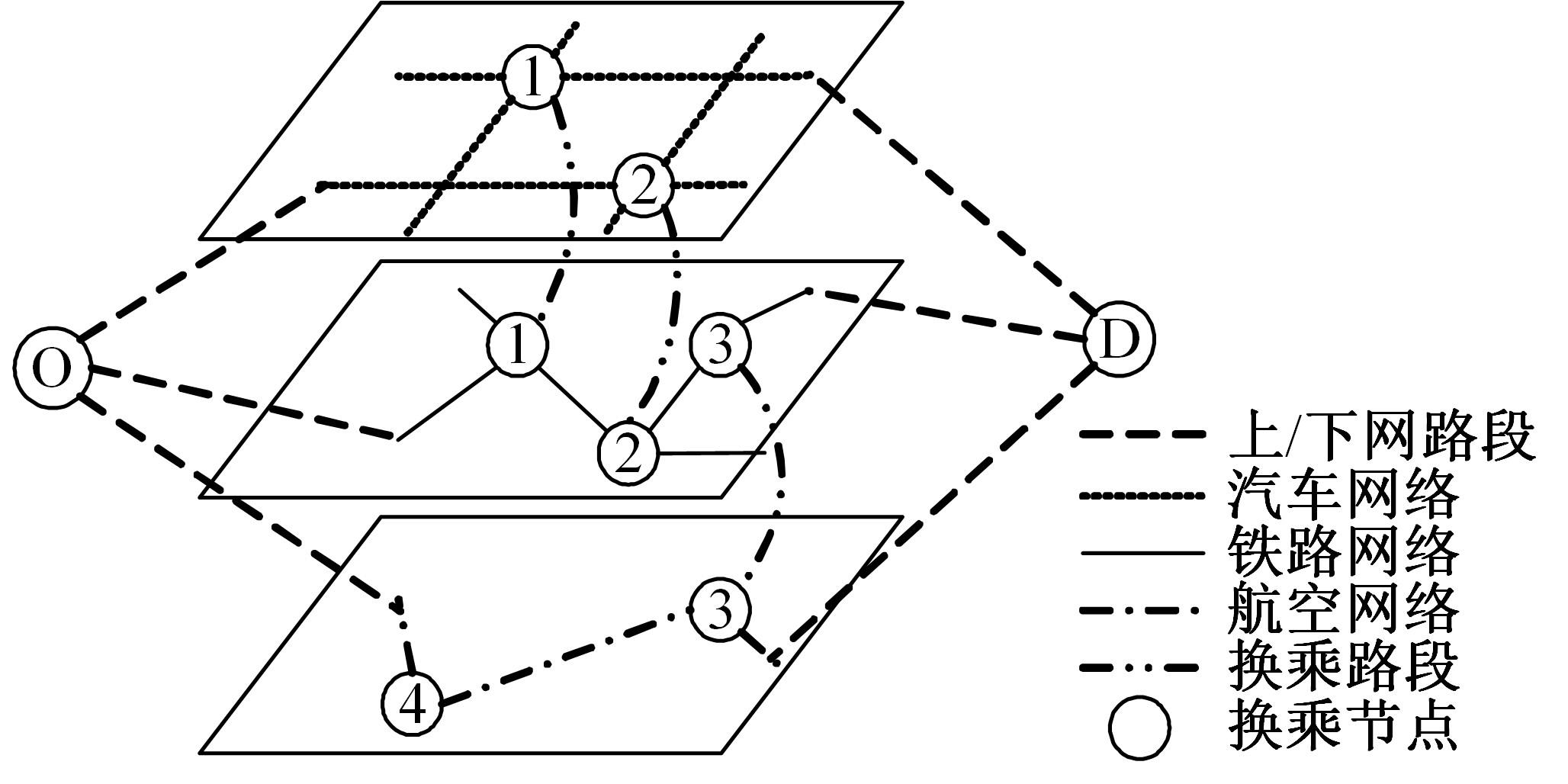
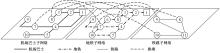
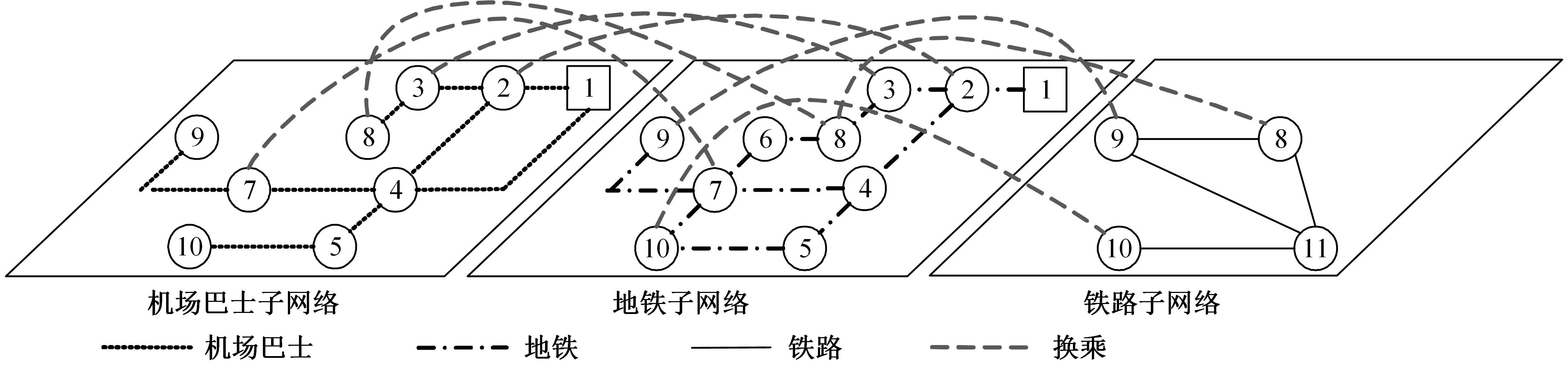
为满足城市群范围内旅客直达出行需求,提出了以多层次轨道交通衔接为基础的直通线路规划方案,探讨了不同方案带来的客运系统增益效果。基于超网络理论构建了城市群超网络模型,量化了旅客超路径的广义出行费用。构建了直通线路最优选择方案的双层规划模型:上层规划综合考虑运输商的利润和设置直通线路所节约的旅客出行成本;下层规划为城市群多方式交通系统的平衡分配模型,采用遗传算法和相继平均法求解上下层模型。最后,以京津冀城市群内衔接主要枢纽的客运线路为例对模型进行有效性验证,对直通线路设置规模的合理性进行论证。结果表明:在北京首都国际机场、北京站、北京西站、北京南站和天津站这5个枢纽之间,可开通备选直通线路11条,最佳直通线路编号为1、2、5、6、7、9;目前合理的直通线路规模为3条,开通之后的系统效益将提升28.03%,旅客平均出行时间降低10.02%。
中图分类号:
- U491.1
| 1 | Vigrass J W. Alternative forms of motive power for suburban rail rapid transit[C]∥ASME/IEEE Joint Conference on Railroads, Chicago, IL, USA, 1990: 259-265. |
| 2 | Griffin T. Light rail transit sharing the railtrack system[J]. Proceedings of the Institution of Civil Engineers-Transport, 1996, 117(2): 98-103. |
| 3 | Current J R, Velle C, Cohon J L. The maximum covering/shortest path problem: a multi-objective network design and routing formulation[J]. European Journal of Operational Research, 1985, 21(2): 189-199. |
| 4 | Gendreau M, Laporte G, Mesa J A. Locating rapid transit lines[J]. Journal of Advanced Transportation, 2010, 29(2): 145-162. |
| 5 | Derrible S, Kennedy C. Network analysis of world subway systems using updated graph theory[J]. Journal of the Transportation Research Board, 2009, 2112(1): 17-25. |
| 6 | 马威. 基于规划紧迫度的京津冀城市群城际铁路网规划研究[D]. 石家庄: 石家庄铁道大学交通运输学院, 2020. |
| Ma Wei. Research on the intercity railway network planning of Beijing Tianjin Hebei urban agglomeration based on the urgency of planning[D]. Shijiazhuang: School of Traffic and Transportation, Shijiazhuang Tiedao University, 2020. | |
| 7 | 周建军, 顾保南. 国外市域轨道交通共线运营方式的发展和启示[J]. 城市轨道交通研究, 2004(6): 75-77. |
| Zhou Jian-jun, Gu Bao-nan. Development of joint operation in foreign metropolitan rail transit[J]. Urban Mass Transit, 2004(6): 75-77. | |
| 8 | 裴玉龙, 马部珍, 杨世军. 基于广义费用的公共交通与私人交通竞争强度研究[J]. 重庆理工大学学报: 自然科学, 2020, 34(1): 169-175. |
| Pei Yun-long, Ma Bu-zhen, Yang Shi-jun. Analysis on the competitiveness of public transport and private transportation of urban residents[J]. Journal of Chongqing University of Technology (Natural Science), 2020, 34(1): 169-175. | |
| 9 | 徐璞. 城市群多方式旅客运输网络能力优化建模及算法研究[D]. 北京:北京交通大学交通运输学院, 2019. |
| Xu Pu. Research on modeling and algorithms for capacity optimization of multi-modal passenger transportation network in urban agglomeration[D]. Beijing: School of Traffic and Transportation, Beijing Jiaotong University, 2019. | |
| 10 | 景云, 孙佳政, 张桢桦. 基于广义费用函数的城际铁路分时定价策略研究[J]. 铁道学报, 2020, 42(5): 29-36. |
| Jing Yun, Sun Jia-zheng, Zhang Zhen-hua. Research on time differential pricing strategy of intercity railway based on generalized cost function[J]. Journal of the China Railway Society, 2020, 42(5): 29-36. | |
| 11 | 汪勤政, 四兵锋. 换乘约束下城市多方式交通分配模型与算法[J]. 交通运输系统工程与信息, 2017, 17(4): 159-165, 181. |
| Wang Qin-zheng, Si Bing-feng. Urban multi-modal traffic assignment model and algorithm under transfer constrain[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(4): 159-165, 181. | |
| 12 | 李虹慧. 京津冀城市群居民城际出行的交通方式选择行为分析[D]. 北京: 北京交通大学交通运输学院, 2020. |
| LI Hong-hui. Choice behavior analysis of transportation modes among residents in Jing-Jin-Ji urban agglomeration[D]. Beijing: School of Traffic and Transportation, Beijing Jiaotong University, 2020. |
| [1] | 贾洪飞,丁心茹,杨丽丽. 城市潮汐车道优化设计的双层规划模型[J]. 吉林大学学报(工学版), 2020, 50(2): 535-542. |
| [2] | 姜攀, 杨家其, 房瑞伟. 城市群综合运输通道布局优化双层模型[J]. 吉林大学学报(工学版), 2017, 47(4): 1061-1067. |
| [3] | 杨兆升, 宋淑敏, 杜鹏程, 杨薇. 大型公共场所应急状态下交通诱导疏散模型 [J]. , 2012, (03): 588-593. |
| [4] | 刘杰, 何世伟, 宋瑞, 蒋金亮. 综合运输体系下的货运网络能力计算[J]. 吉林大学学报(工学版), 2012, 42(02): 334-338. |
| [5] | 于滨, 杨忠振, 程春田, 左志 . 公交线路发车频率优化的双层规划模型及其解法[J]. 吉林大学学报(工学版), 2006, 36(05): 664-0668. |
|
||