城市潮汐车道优化设计的双层规划模型

doi:10.13229/j.cnki.jdxbgxb20180790

摘要/Abstract

摘要：

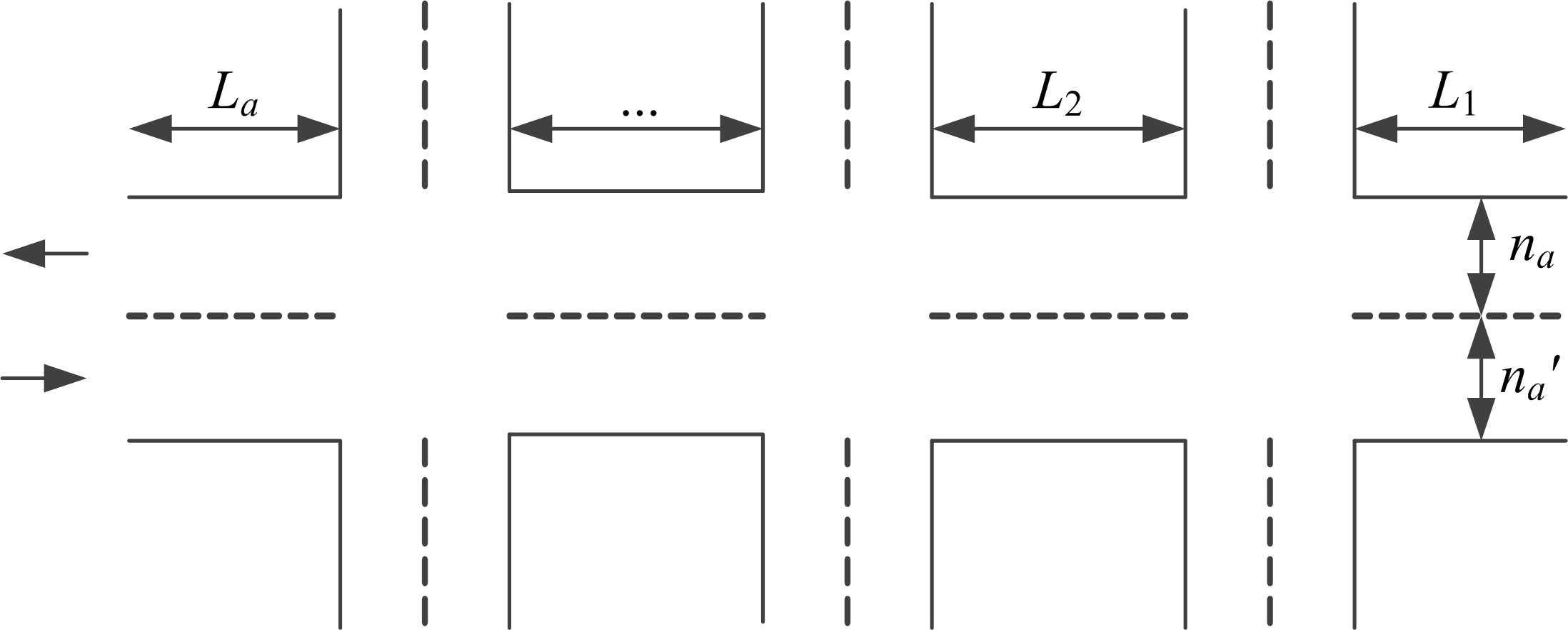
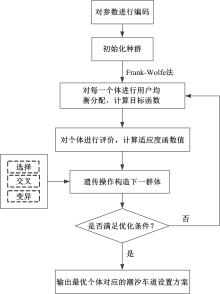
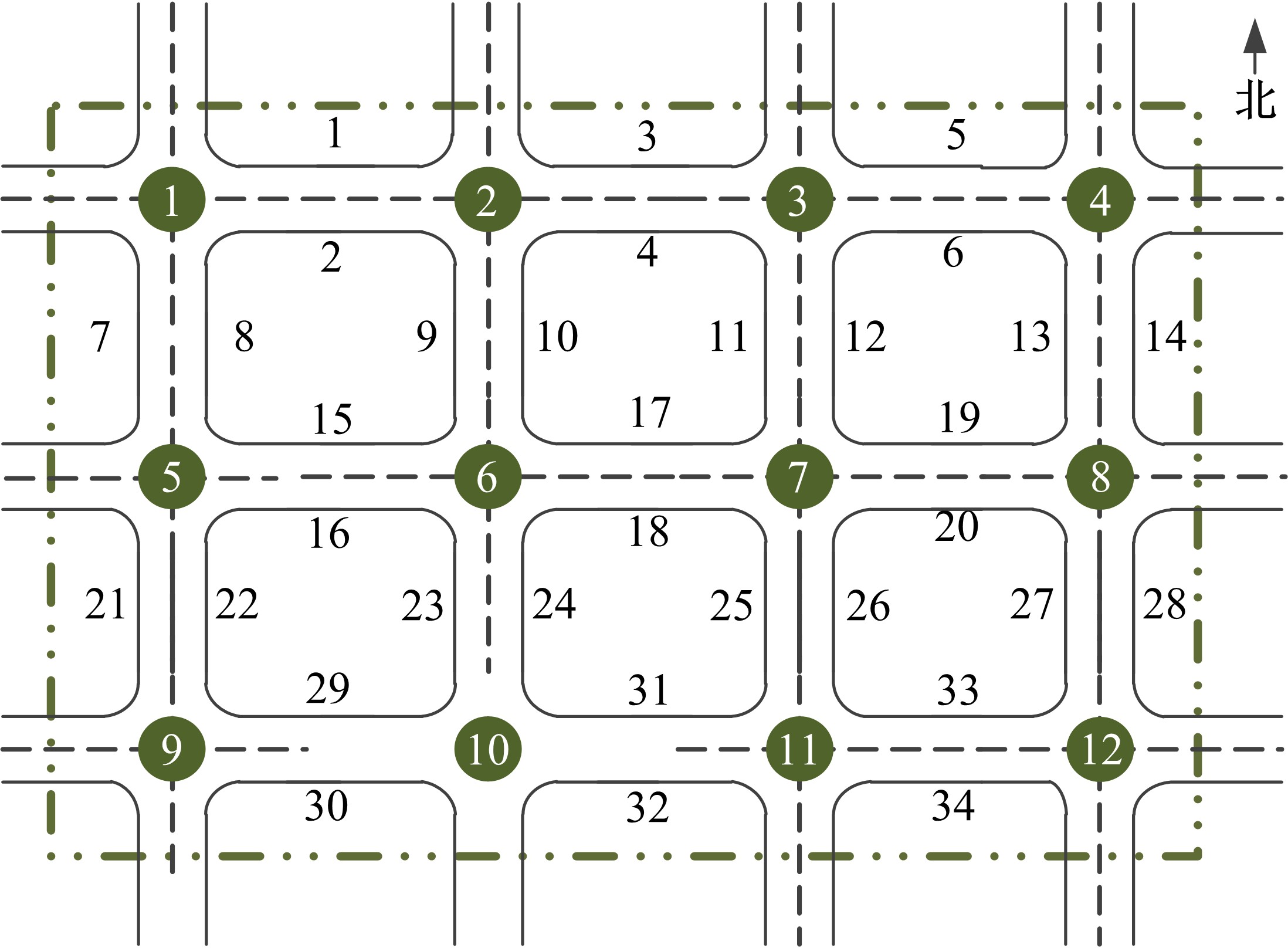
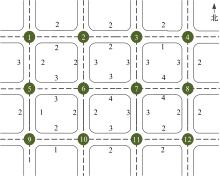
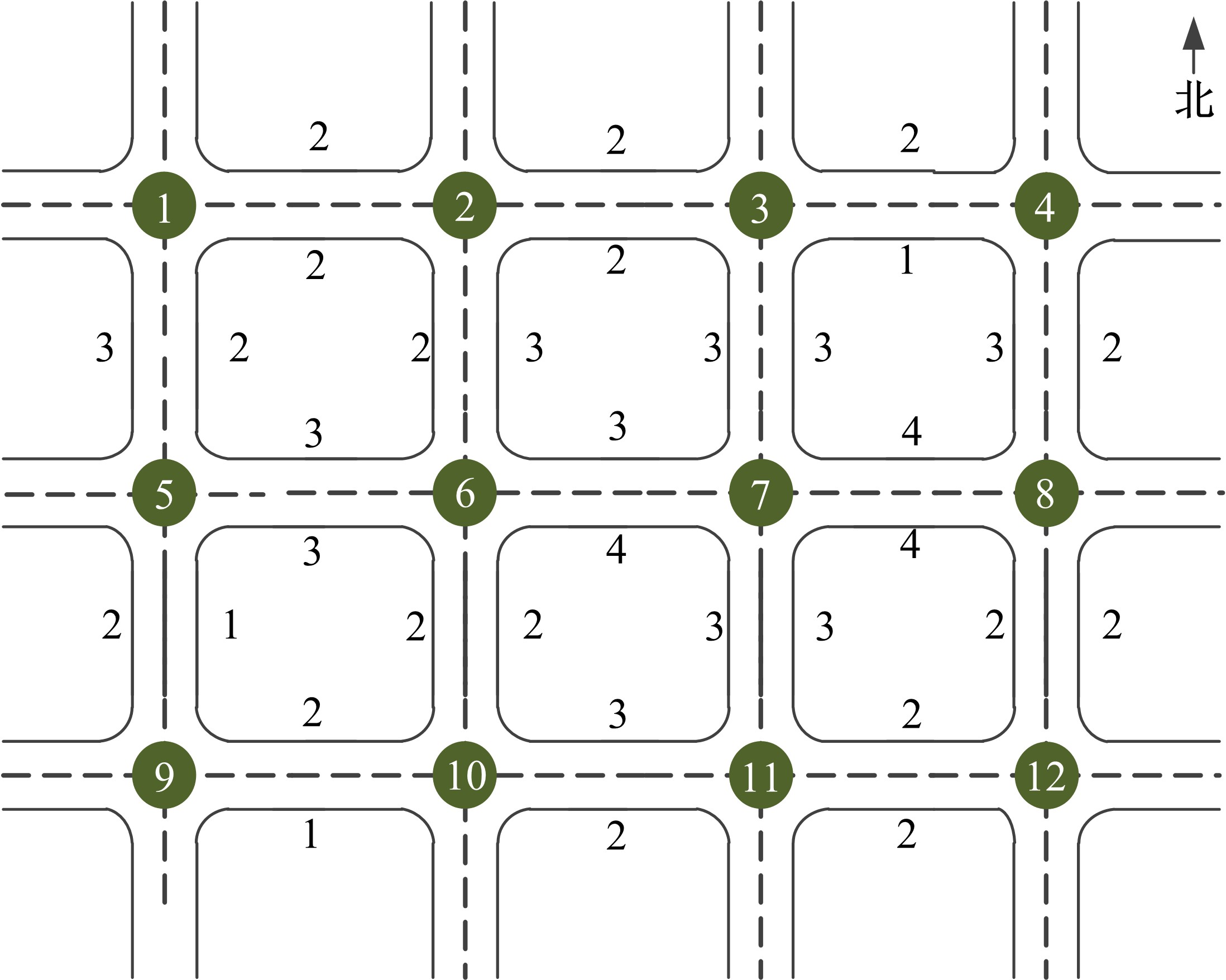
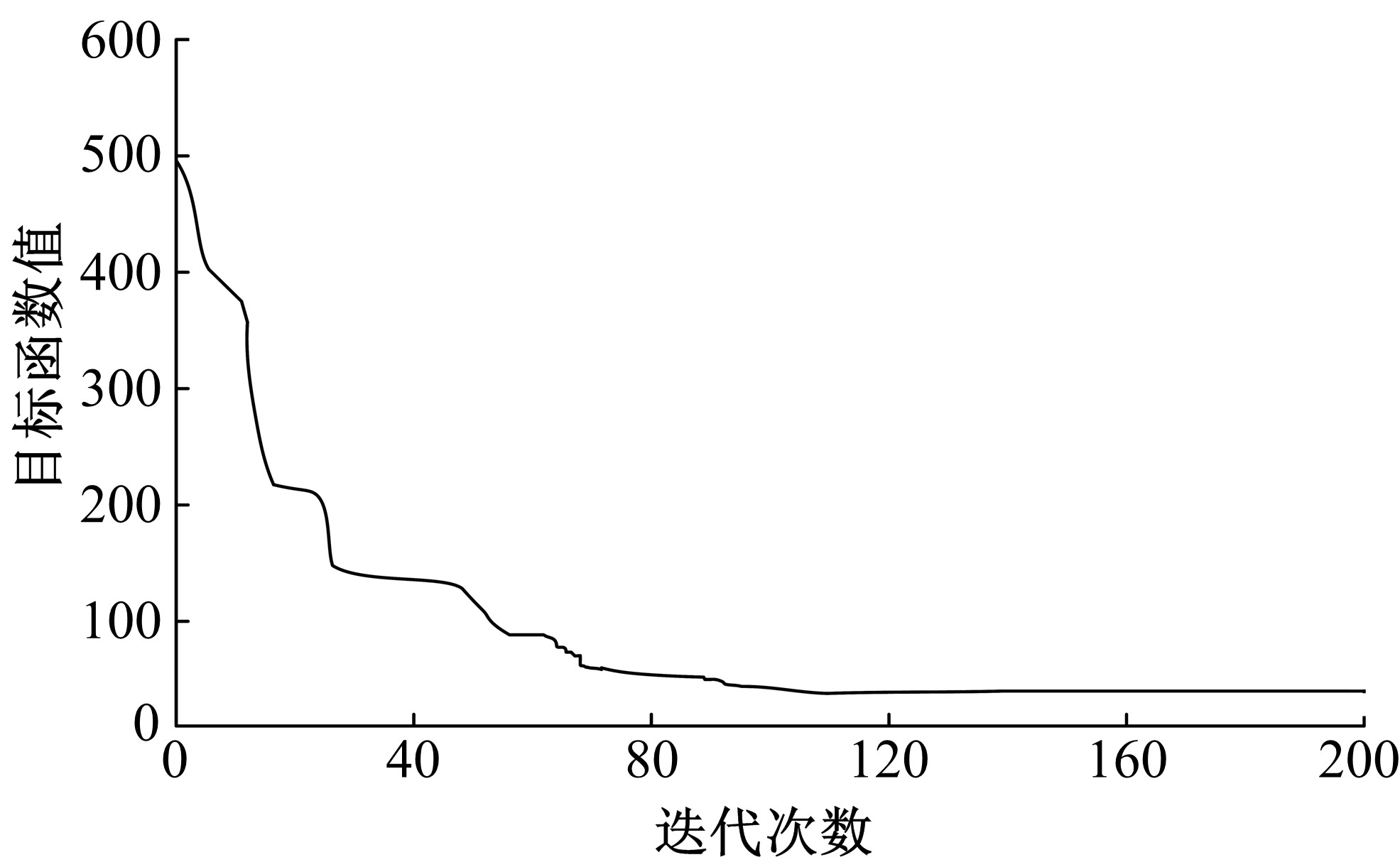
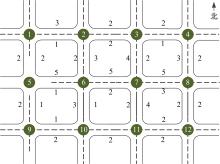
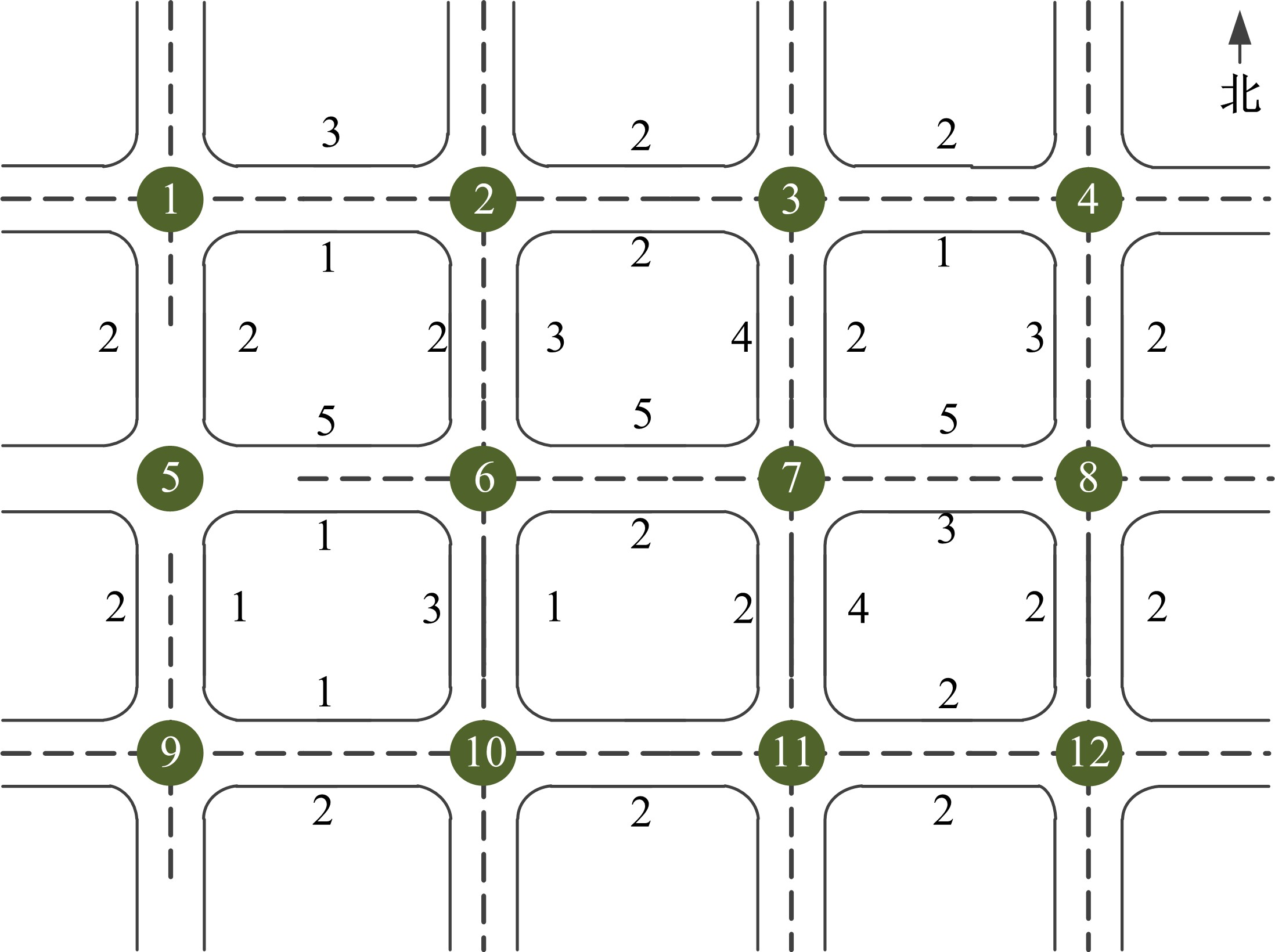
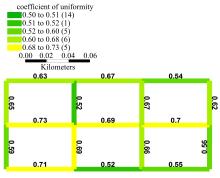
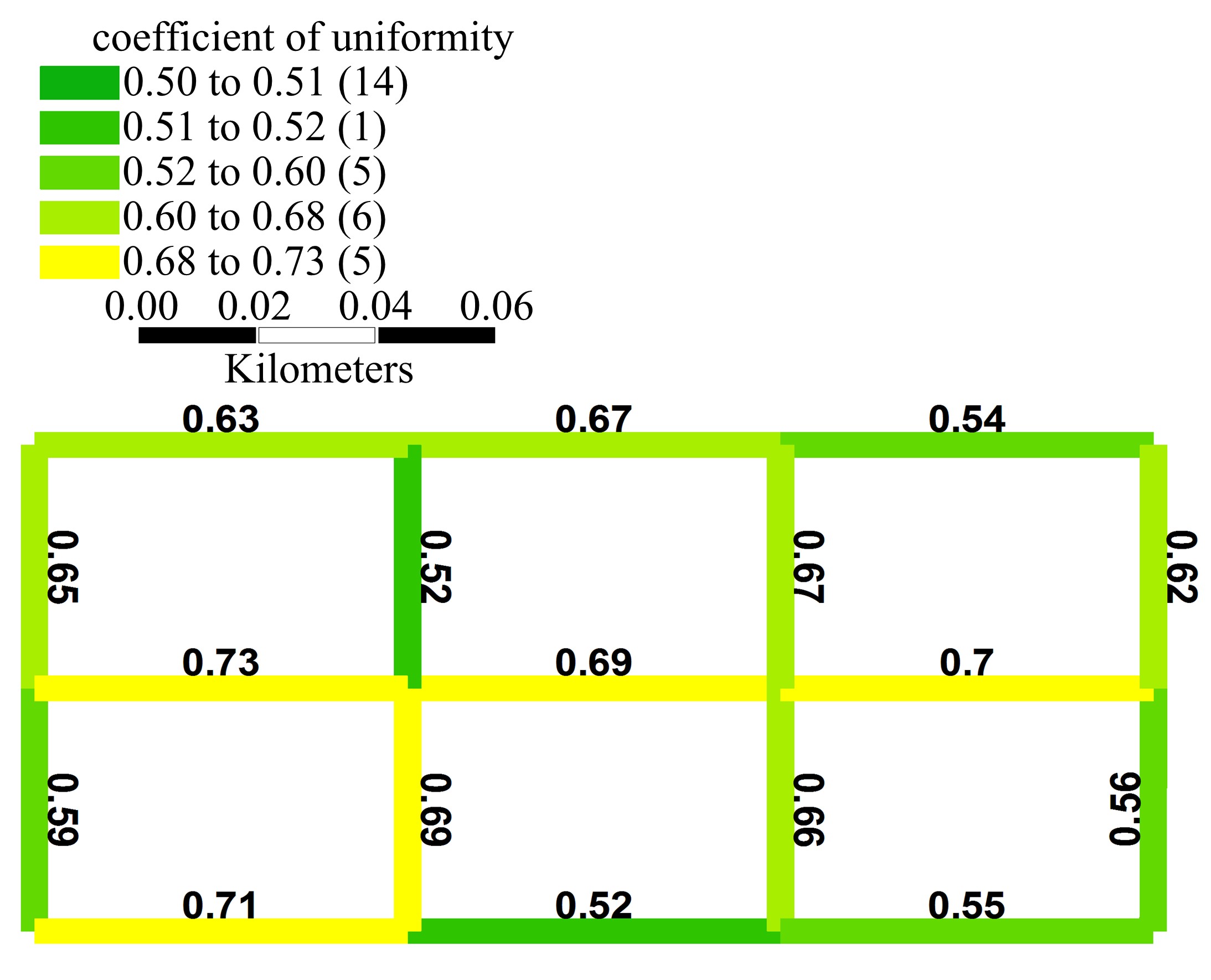
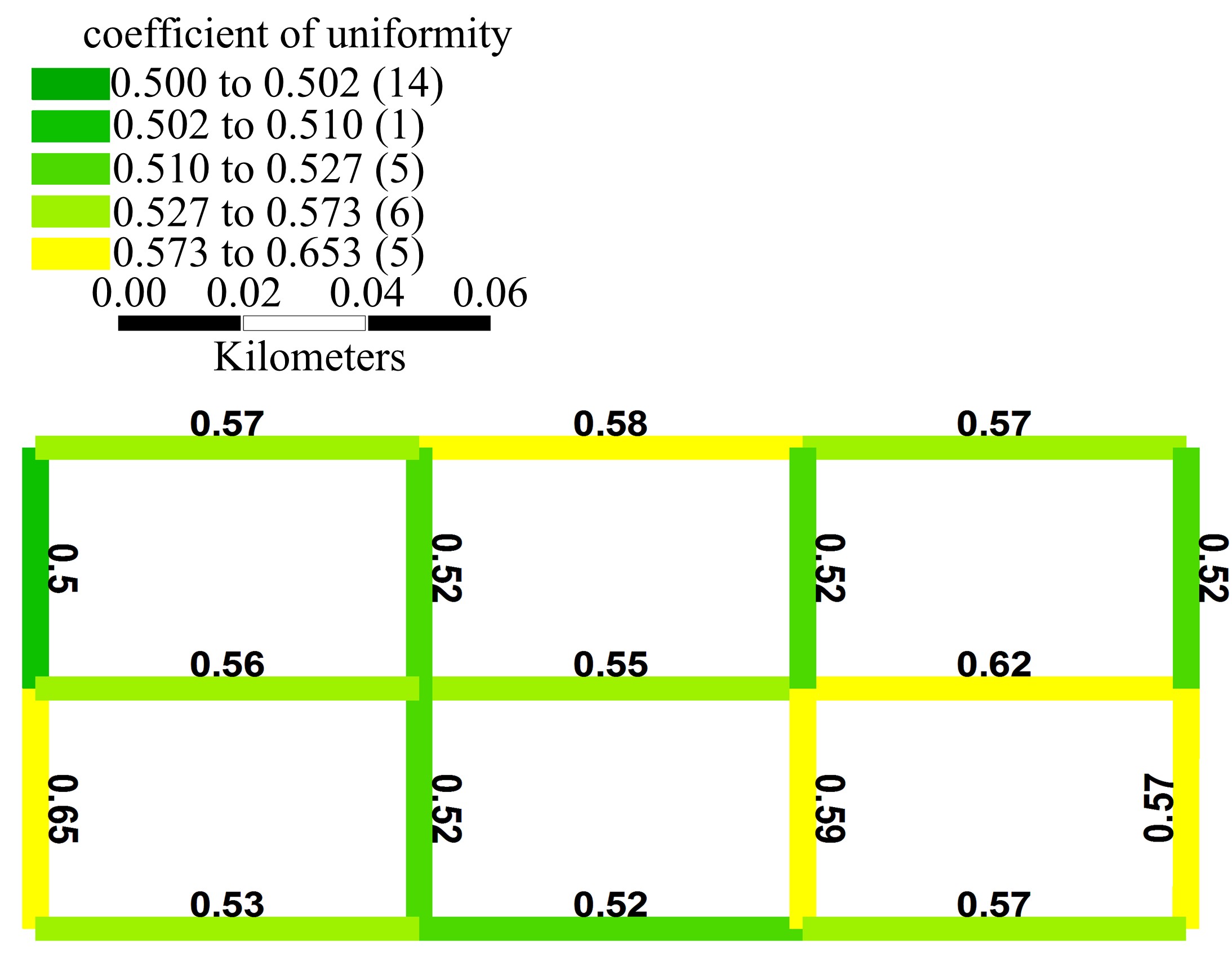
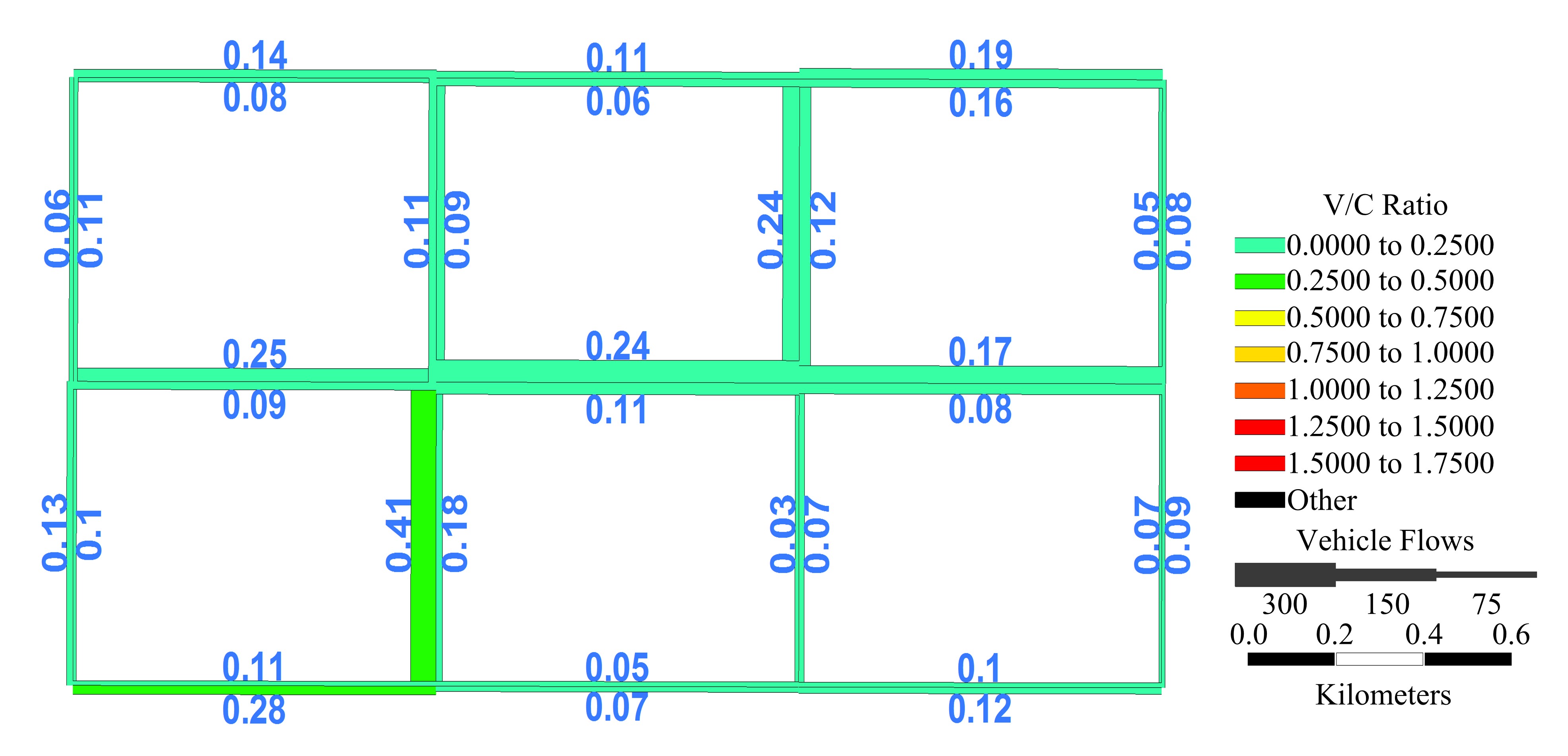
针对周期性某时段路段通行能力不均衡所导致的单向拥堵问题，分析了潮汐车道的设置条件与方向分布系数。在此基础上，从路网系统的角度出发，建立潮汐车道设置方案的双层规划模型，上层模型用于路网车道分配，以系统总延误及潮汐车道交通流优化比的和最优为目标，下层模型为路径选择行为符合Wardrop用户平衡准则的用户均衡分配模型。基于遗传算法和Frank-Wolfe算法进行算例分析，并将优化前、后的方向分布系数与路段饱和度进行对比，结果表明：该模型可合理缓解潮汐交通现象，降低路网系统总延误。

关键词: 交通运输系统工程, 潮汐车道, 双层规划模型, 遗传算法

Abstract:

In order to solve the unidirectional traffic congestion due to uneven road traffic capacity, The tidal lane setting conditions and coefficient of direction uniformity were analyzed. The tidal lane of bi-level programming model is established from the perspective of network system. In the model, the upper-level is applied to optimize the sum of the system delay and tidal lane utilization ratio, and the lower-level is designed by user equilibrium allocation model whose path selection behavior conforms to the Wardrop principle. The iterative algorithm integrating a genetic algorithm and a Frank-Wolfe algorithm is used to solve the lower and upper models. A case study is implemented to test the efficiency of the model, the coefficient of direction uniformity and road saturation before and after optimization are compared. The results show that the model can reasonably alleviate the phenomenon of tidal traffic and reduce the total delay of the road network system.

Key words: engineering of communications and transportation system, tidal lane, bi-level programming mode, genetic algorithm

中图分类号:

U491.5

贾洪飞,丁心茹,杨丽丽. 城市潮汐车道优化设计的双层规划模型[J]. 吉林大学学报(工学版), 2020, 50(2): 535-542.

Hong-fei JIA,Xin-ru DING,Li-li YANG. Bi-level programming model for optimization design of tidal lane[J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(2): 535-542.

图/表 14

图1

图2

图3

图4

图5

表1

算例网络自由流时间表"

路段	自由流时间 $t a$ /h	路段	自由流时间 $t a$ /h
1和2	0.02	19和20	0.05
3和4	0.04	21和22	0.03
5和6	0.03	23和24	0.08
7和8	0.02	25和26	0.05
9和10	0.05	27和28	0.03
11和12	0.07	29和30	0.02
13和14	0.02	31和32	0.05
15和16	0.05	33和34	0.01
17和18	0.10

表1

表2

图6

表3

图7

图8

图9

图10

图11

参考文献 21

1	刘鹏，刘英舜. 潮汐式交通特性分析及应对措施研究[J]. 交通科技与经济, 2011, 13(3): 92-94.
	Liu Peng, Liu Ying-shun. Study on characters of tidal transpotation and relieve meatures[J]. Technology & Economy in Areas of Communications, 2011, 13(3): 92-94.
2	Stone P, Fajardo D, Hausknecht M, et al. Dynamic lane reversal in traffic management[J]. International IEEE Conference on Intelligent Transportation Systems, 2014, 263(4): 1929-1934.
3	刘恋. 可变车道优化控制研究[D]. 大连：大连交通大学交通运输工程学院， 2014.
	Liu Lian. The reseach on optimal control of variable lane[D]. Dalian: School of Traffic and Transportation Engineering, Dalian Jiaotong University, 2014.
4	崔凯. 左转逆向可变车道的优化设计与控制策略[D]. 山东: 山东大学控制科学与工程学院, 2017.
	Cui Kai. Optimal design and control strategy of left-turn reverse variable lane[D]. Shandong: Department of Control Science and Engineering, Shandong University, 2017.
5	Habibollah N, Ali E, Hamed A. Estimation of the logit model for the online contra flow problem[J]. Transport, 2010, 25(4): 433-441.
6	Matthew H, Au T C, Stone P. Dynamic lane teversal in yraffic management[J]. IEEE Conference on Intelligent Transportation Systems, 2011, 16(7): 1929-1934.
7	高瑞, 龙建成. 基于可变车道优化的交通网络设计问题[J]. 合肥工业大学学报：自然科学版, 2015, 38(11): 1446-1450.
	Gao Rui, Long Jian-cheng. A Transportation network design problem with optimization of variable lanes[J]. Journal of Hefei University of Technology （Natural Science）, 2015, 38(11): 1446-1450.
8	曲大义, 曹俊业, 王进展, 等. 潮汐车道与变向车道协同优化的绿波控制方法[J]. 济南大学学报：自然科学版, 2017, 31(3): 208-214.
	Qu Da-yi, Cao Jun-ye, Wang Jin-zhan, et al. Green wave control method of collaborative optimization of tidal lane and variable lane[J]. Journal of University of Jinan （Science and Technology）, 2017, 31(3): 208-214.
9	Wang J W, Wang H F, Zhang W J, et al. Evacuation planning based on the contra flow technique with consideration of evacuation priorities and traffic setup time[J]. IEEE Transactions on Intelligeng Transportation Systems, 2013, 14(1): 480-485.
10	Konstantinos A, Henrique S F, Rodrigo C C. Motorway tidal flow lane control[J]. IFAC-PapersOnLine, 2018, 51(9): 279-284.
11	张鹏, 李文权, 常玉林. 可变车道的城市路网备用容量模型[J]. 西南交通大学学报, 2010, 45(2): 255-260.
	Zhang Peng, Li Wen-quan, Chang Yu-lin. Reserve capacity model for urban road network with variable lanes[J]. Journal of Southwest Jiaotong University, 2010, 45(2): 255-260.
12	Gao Z Y, Song Y F. A reserve capacity model of optimal signal control with user equilibrium route choice[J]. Transportation Research Part B, 2002, 36(4): 313-323.
13	NCHRP. Convertle Roadways and Lanes[R]. Washington DC: Transportation Research Board of the National Academies, 2004.
14	王勇. 城市交通网络可变车道设置方案研究[D]. 成都：西南交通大学交通运输与物流学院, 2014.
	Wang Yong. Research for reversible lane plan in urban traffic network[D]. Chengdu: School of Transportation and Logistics, Southwest Jiaotong University, 2014.
15	曹俊业. 基于潮汐流特性的变向车道协同优化控制方法[D]. 青岛：青岛理工大学机械与汽车工程学院, 2016.
	Cao Jun-ye. Control method of variable lane cooperation based on the characteristics of tidal flow[D]. Qingdao: School of Mechanical and Aotomotive Engineering, Qingdao University of Technology, 2016.
16	王雄. 城市道路可变车道设置的一主二从双层规划模型与算法[D]. 长沙：中南大学交通运输工程学院, 2013.
	Wang Xiong. Bi-level programming model and algorithm of urban roads convertible lanes[D]. Changsha: School of Traffic and Transportation Engineering, Central South University, 2013.
17	代磊磊, 顾金刚, 俞春俊, 等. 潮汐车道交通流特性与设置方案仿真研究[J]. 交通信息与安全, 2012, 30(1): 15-19.
	Dai Lei-lei, Gu Jin-gang, Yu Chun-jun, et al. Traffic flow characteristics on reversible lane and its operational plan based on simulation[J]. Journal of Transport Information and Safety, 2012, 30(1): 15-19.
18	陈雪珍. 基于双层规划的城市轨道交通接驳公交线路研究[D]. 南昌：华东交通大学交通运输与物流学院, 2016.
	Chen Xue-zhen. Research of urban rail transit feeder bus routes based on bi-level programming[D]. Nanchang： School of Transportation and Logistics, East China Jiaotong University, 2016.
19	李和成, 王宇平. 求解混合整数双层规划问题的遗传算法[J]. 吉林大学学报: 工学版, 2009, 39(3): 781-786.
	Li He-cheng, Wang Yu-ping. Genetic algorithms for solving mixed-integer bilevel programming problems[D]. Journal of Jilin University (Engineering and Technology Edition), 2009, 39(3): 781-786.
20	董海隆. 大型市政工程施工期间交通微循环改善研究[D]. 兰州：兰州交通大学交通运输学院, 2013.
	Dong Hai-long. The research of transportation microcirculation improvement during the large-scale municipal construction[D]. Lanzhou: School of Traffic and Transportation, Lanzhou Jiaotong University, 2013.
21	祁宏生, 王殿海, 宋现敏. 路网交通状态平衡控制方法[J]. 吉林大学学报: 工学版, 2012, 42(5): 1185-1190.
	Qi Hong-sheng, Wang Dian-hai, Song Xian-min. Balanced control method for road network traffic state[J]. Journal of Jilin University (Engineering and Technology Edition), 2012, 42(5): 1185-1190.

相关文章 15

[1]	常玉林,袁才鸿,孙超,张鹏. 基于改进元胞传输模型的城市路网实际阻抗计算方法[J]. 吉林大学学报(工学版), 2020, 50(1): 132-139.
[2]	宗长富,文龙,何磊. 基于欧几里得聚类算法的三维激光雷达障碍物检测技术[J]. 吉林大学学报(工学版), 2020, 50(1): 107-113.
[3]	隋振,姜源. 基于MIMO类脑情感学习回路的横-纵向综合控制驾驶员模型[J]. 吉林大学学报(工学版), 2020, 50(1): 140-146.
[4]	别一鸣,姜凯,汤茹茹,王琳虹,熊昕宇. 考虑方案过渡影响的单点交通控制时段划分方法[J]. 吉林大学学报(工学版), 2019, 49(6): 1844-1851.
[5]	贾富淳,孟宪皆,雷雨龙. 基于多目标遗传算法的二自由度动力吸振器优化设计[J]. 吉林大学学报(工学版), 2019, 49(6): 1969-1976.
[6]	谷远利, 张源, 芮小平, 陆文琦, 李萌, 王硕. 基于免疫算法优化LSSVM的短时交通流预测[J]. 吉林大学学报(工学版), 2019, 49(6): 1852-1857.
[7]	程国柱, 冯思鹤, 冯天军. 占用车行道的路内停车泊位设置条件[J]. 吉林大学学报(工学版), 2019, 49(6): 1858-1864.
[8]	马芳武,韩露,周阳,王世英,蒲永锋. 采用聚乳酸复合材料的汽车零件多材料优化设计[J]. 吉林大学学报(工学版), 2019, 49(5): 1385-1391.
[9]	龙海波,杨家其,赵学彧. 基于转运延误风险的多方式协同货运载运工具配置优化[J]. 吉林大学学报(工学版), 2019, 49(5): 1492-1499.
[10]	别一鸣,汤茹茹,王运豪,文斌,冯天军,王琳虹. 信号交叉口进口车道饱和流率估计方法[J]. 吉林大学学报(工学版), 2019, 49(5): 1459-1464.
[11]	梁泉,翁剑成,周伟,荣建. 基于关联规则的公共交通通勤稳定性人群辨识[J]. 吉林大学学报(工学版), 2019, 49(5): 1484-1491.
[12]	王宏志,姜方达,周明月. 基于遗传粒子群优化算法的认知无线电系统功率分配[J]. 吉林大学学报(工学版), 2019, 49(4): 1363-1368.
[13]	吴文静,陈润超,贾洪飞,罗清玉,孙迪. 车路协同环境下路段掉头区域车辆协同控制[J]. 吉林大学学报(工学版), 2019, 49(4): 1100-1106.
[14]	江亮,贺宜. 电动两轮车风险驾驶行为及事故影响因素分析[J]. 吉林大学学报(工学版), 2019, 49(4): 1107-1113.
[15]	曲昭伟,潘昭天,陈永恒,陶鹏飞,孙迪. 基于最优速度模型的改进安全距离跟驰模型[J]. 吉林大学学报(工学版), 2019, 49(4): 1092-1099.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

	1	2	3	4	5	6	7	8	9	10	11	12
1	0.00	3.54	2.39	0.29	2.07	16.57	17.66	5.95	23.18	10.09	1.66	0.25
2	4.84	0.00	1.92	7.53	1.31	9.63	11.78	11.09	7.89	13.25	1.15	0.92
3	6.04	3.58	0.00	21.44	3.46	11.10	7.75	20.16	13.40	16.05	12.50	0.61
4	1.06	5.40	7.26	0.00	1.44	5.32	4.61	8.50	7.04	24.08	17.69	0.24
5	4.45	0.97	9.14	1.02	0.00	1.15	2.48	5.47	35.57	21.79	0.15	0.66
6	1.35	1.70	30.95	4.32	8.50	0.00	38.99	18.89	27.10	13.50	3.74	2.02
7	1.08	7.43	4.60	2.06	2.15	23.98	0.00	3.40	7.00	32.10	1.82	1.10
8	37.39	8.29	35.06	3.70	4.96	13.08	54.73	0.00	3.89	51.79	3.58	1.68
9	20.59	6.00	19.63	3.53	20.64	57.66	6.98	3.63	0.00	11.14	3.31	1.78
10	7.49	8.86	8.29	1.87	28.55	22.04	26.69	37.18	8.80	0.00	40.98	2.92
11	17.46	2.26	27.36	15.61	0.66	7.77	6.21	13.13	9.52	41.26	0.00	5.42
12	0.18	0.25	0.06	0.04	0.42	1.20	0.90	1.31	1.48	1.77	0.52	0.00