曲线盾构隧道施工期地表位移计算方法及影响因素分析

doi:10.13229/j.cnki.jdxbgxb.20221217

摘要/Abstract

摘要：

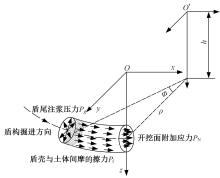
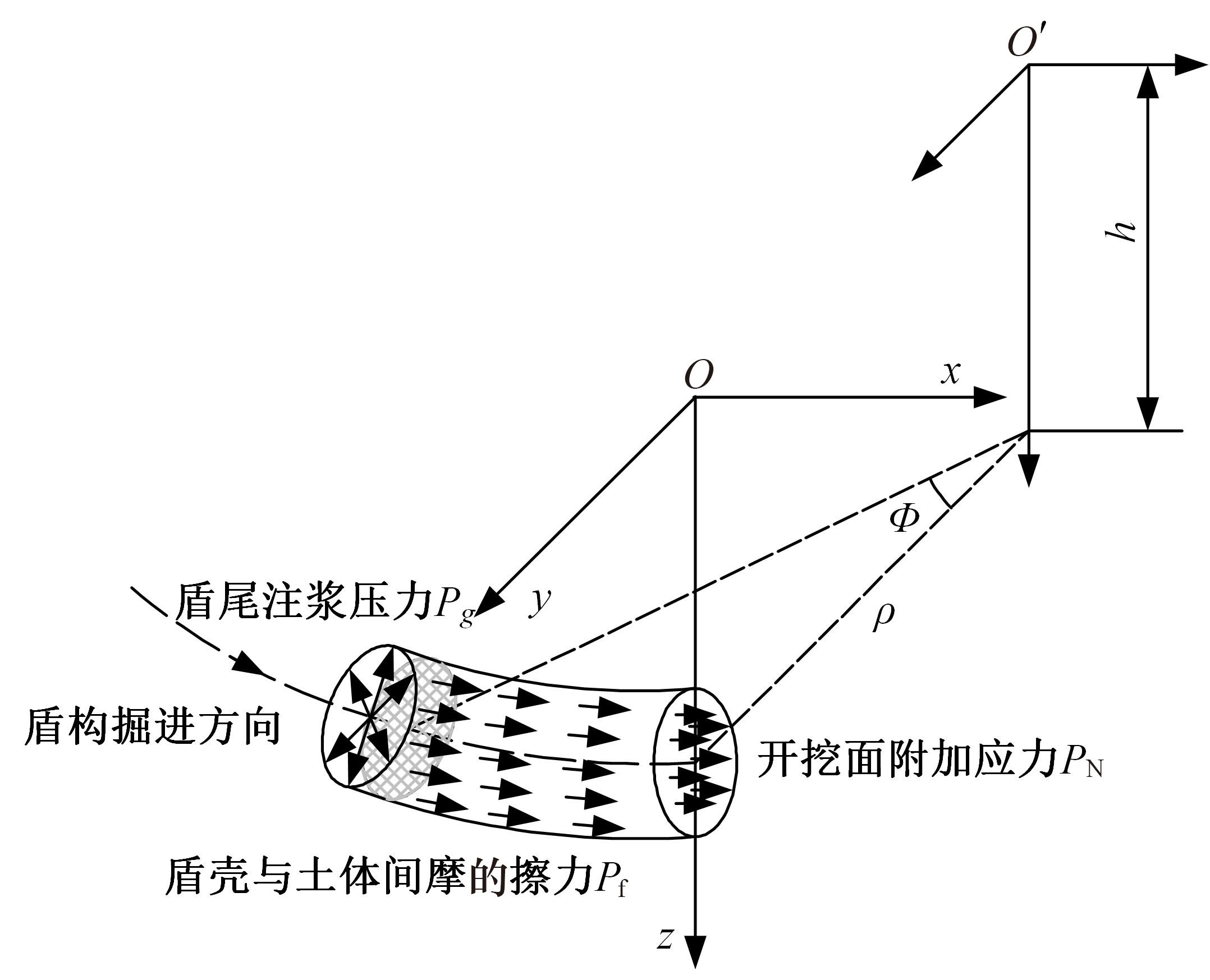
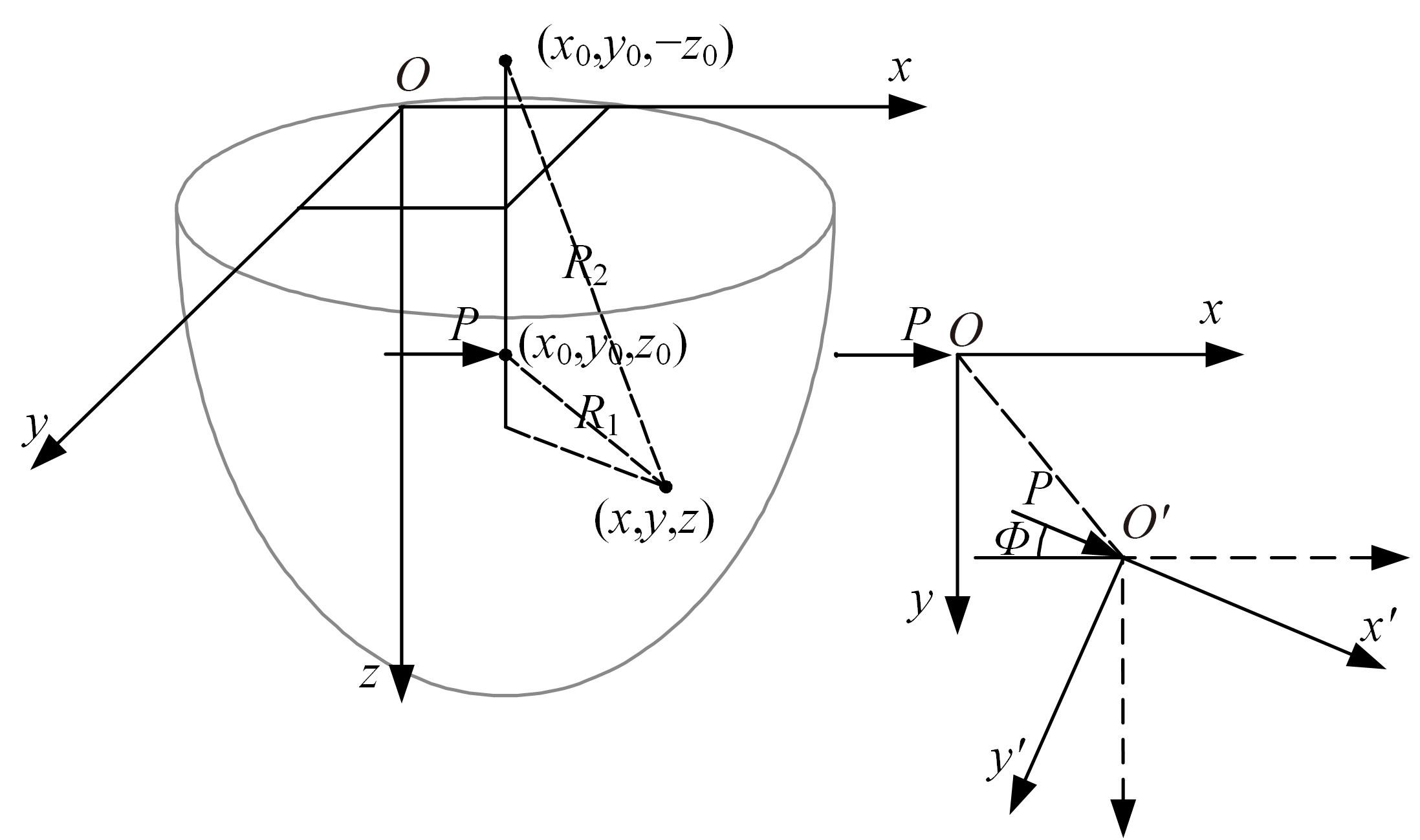
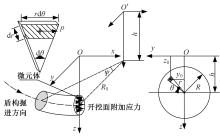
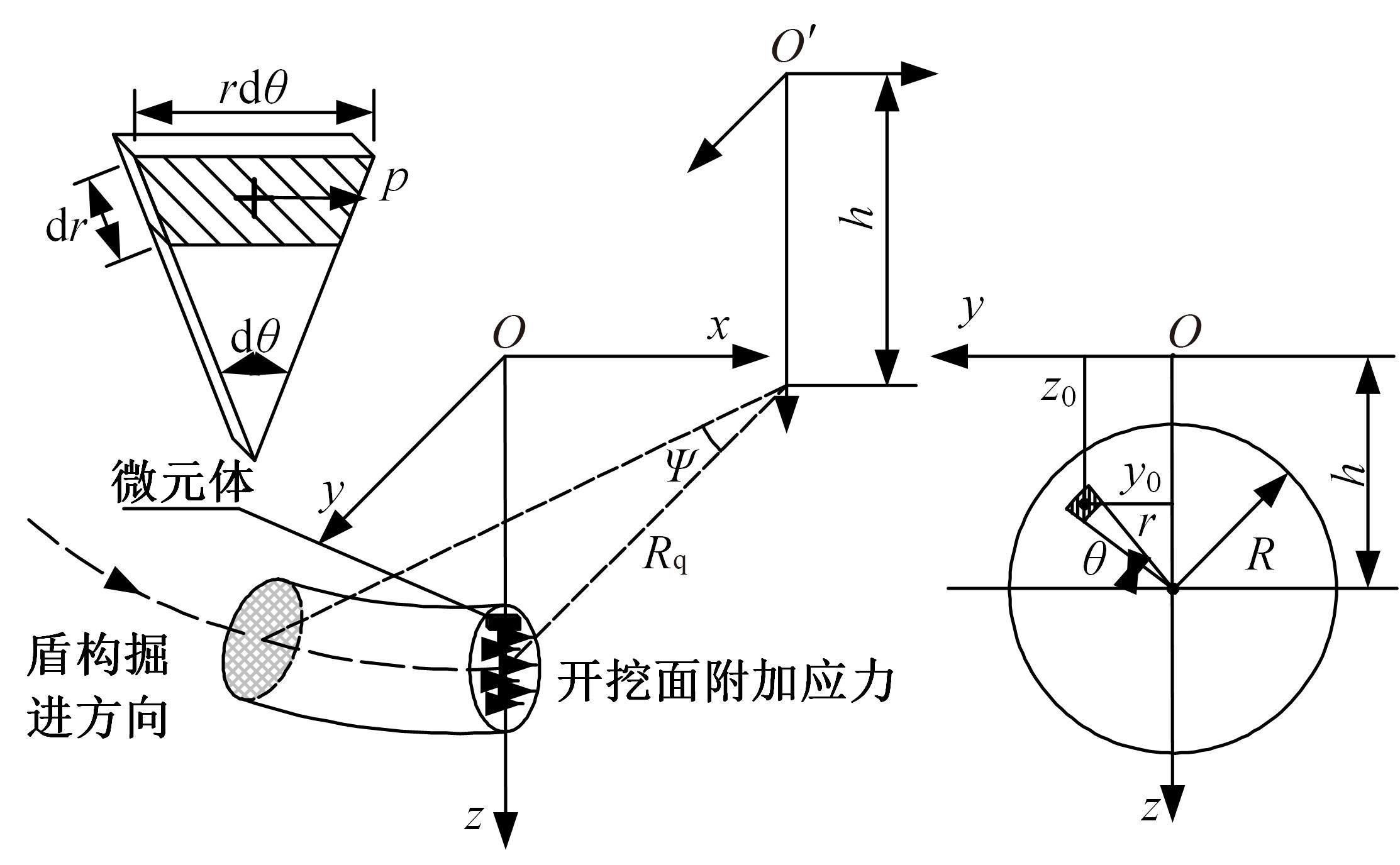
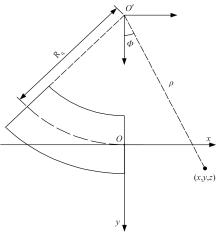
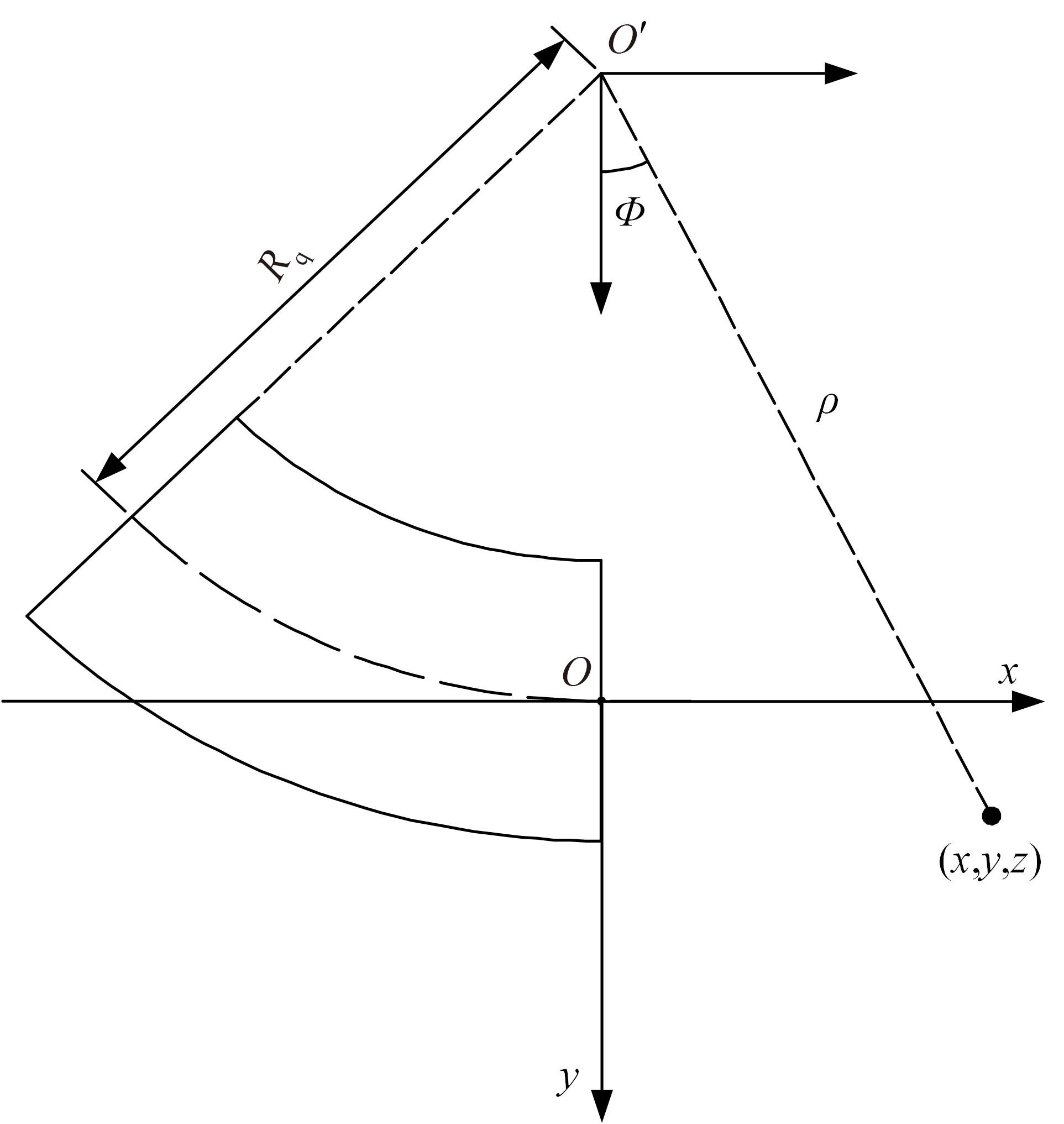
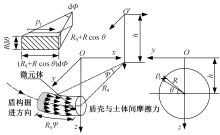
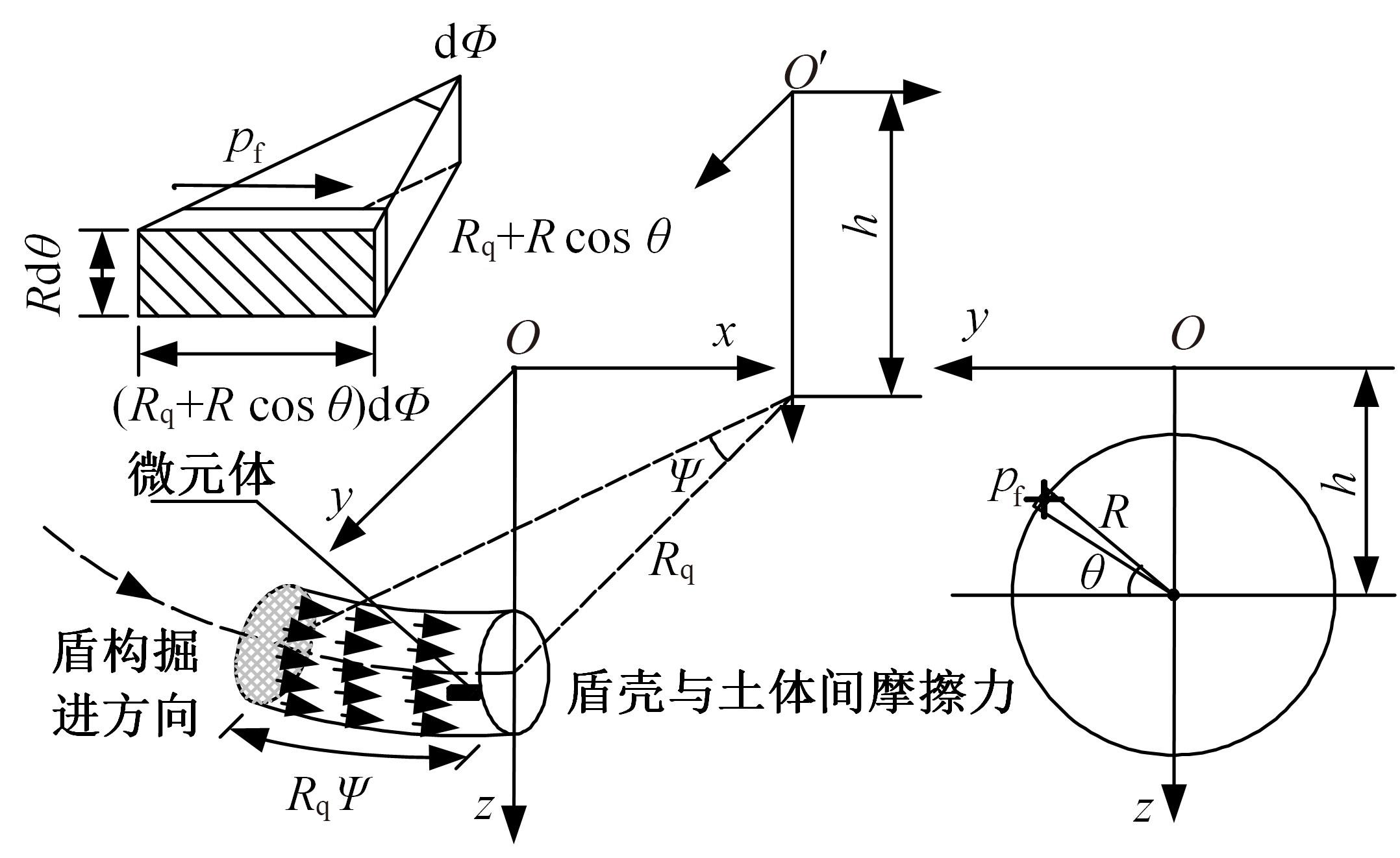
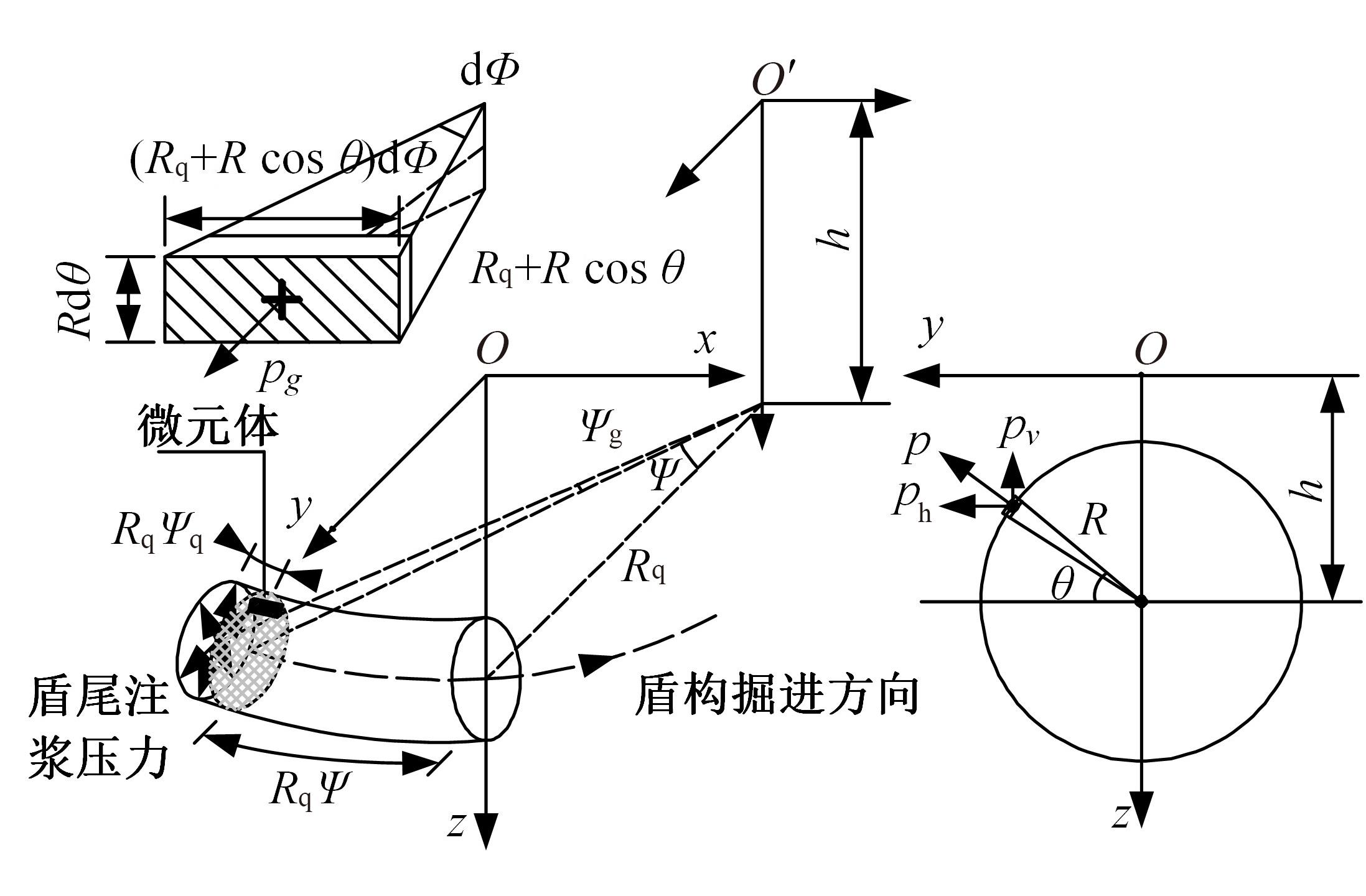
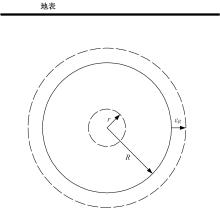
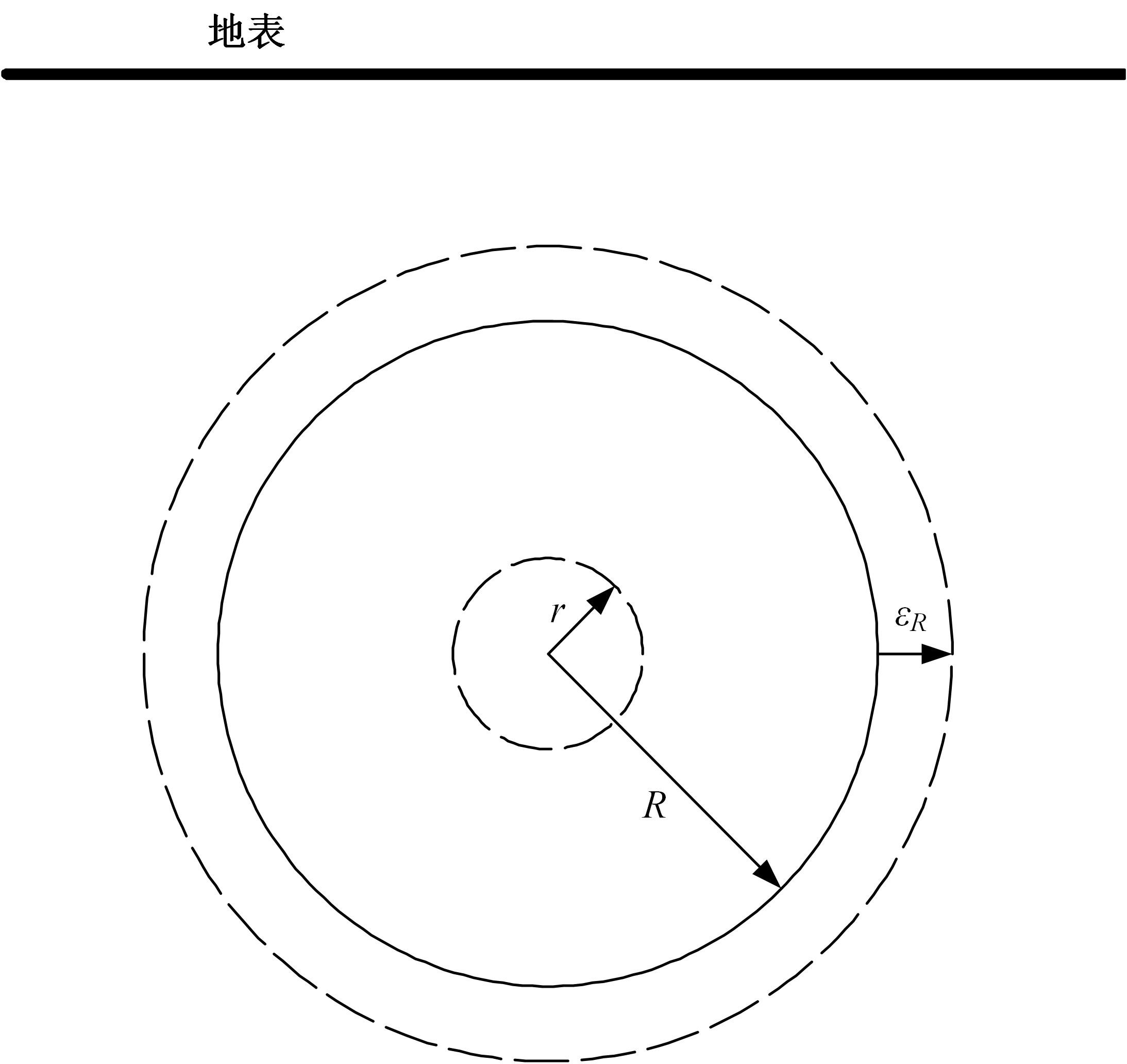
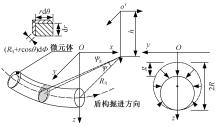
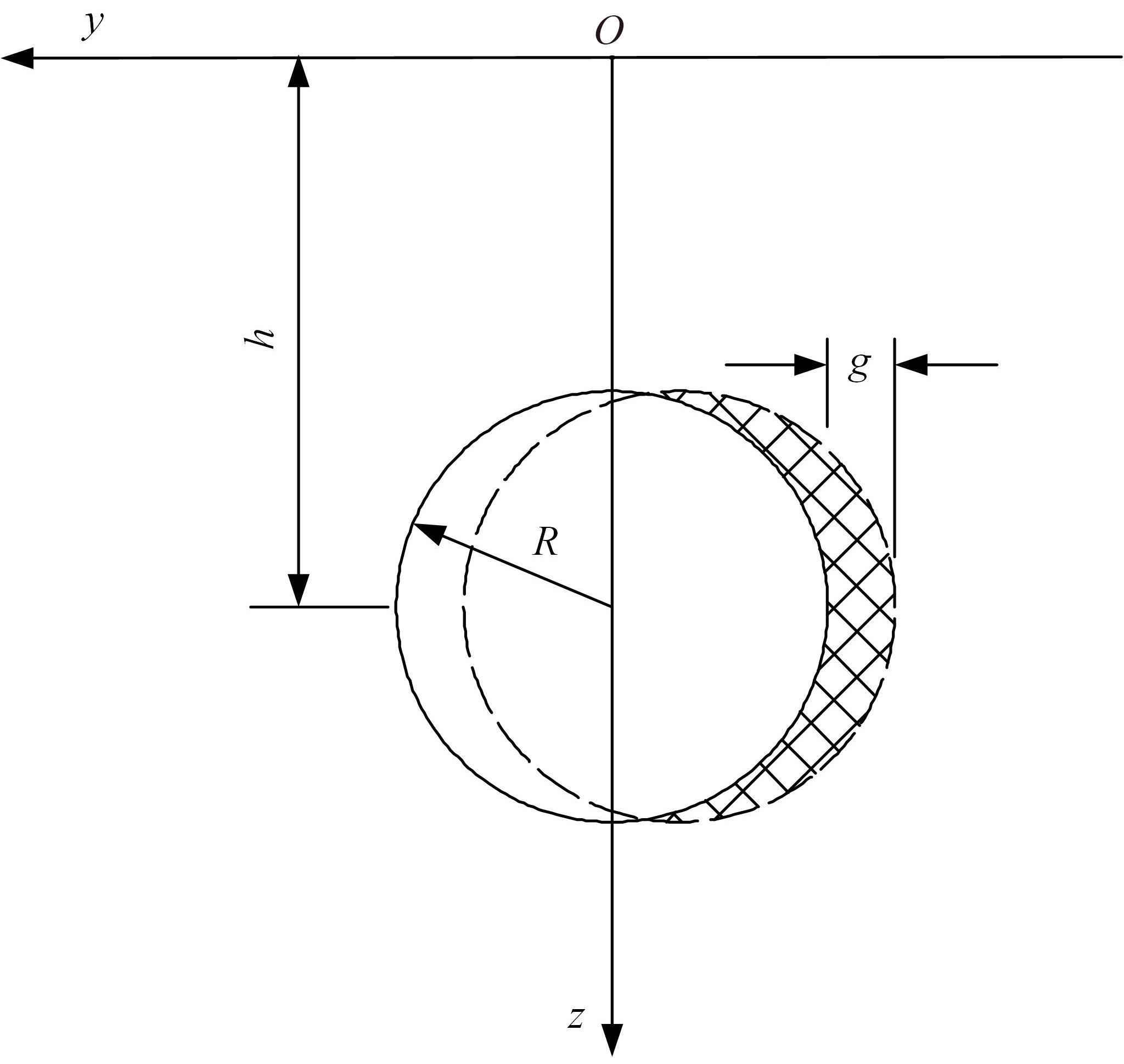
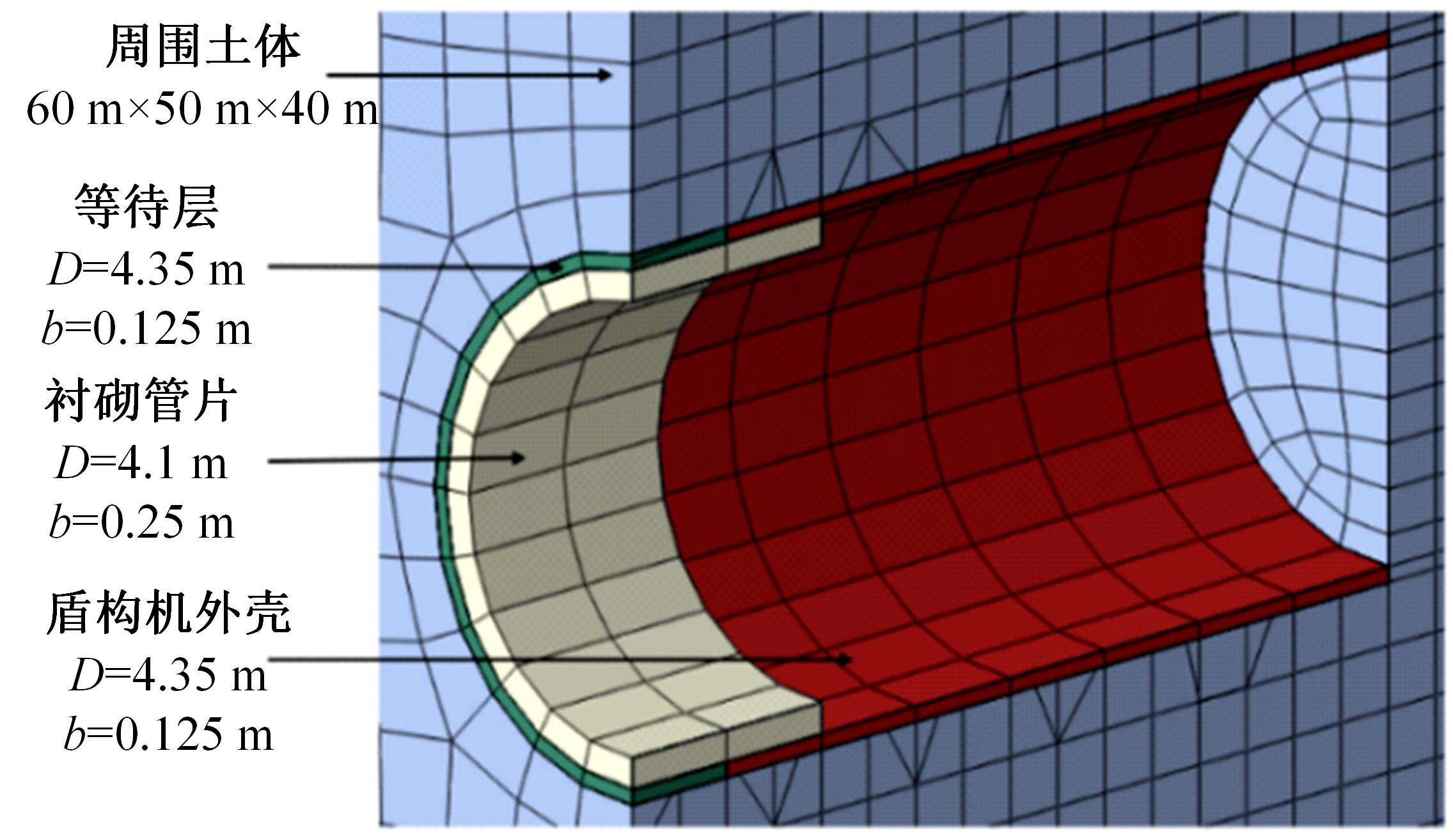
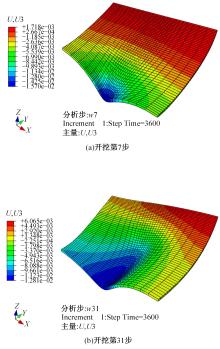
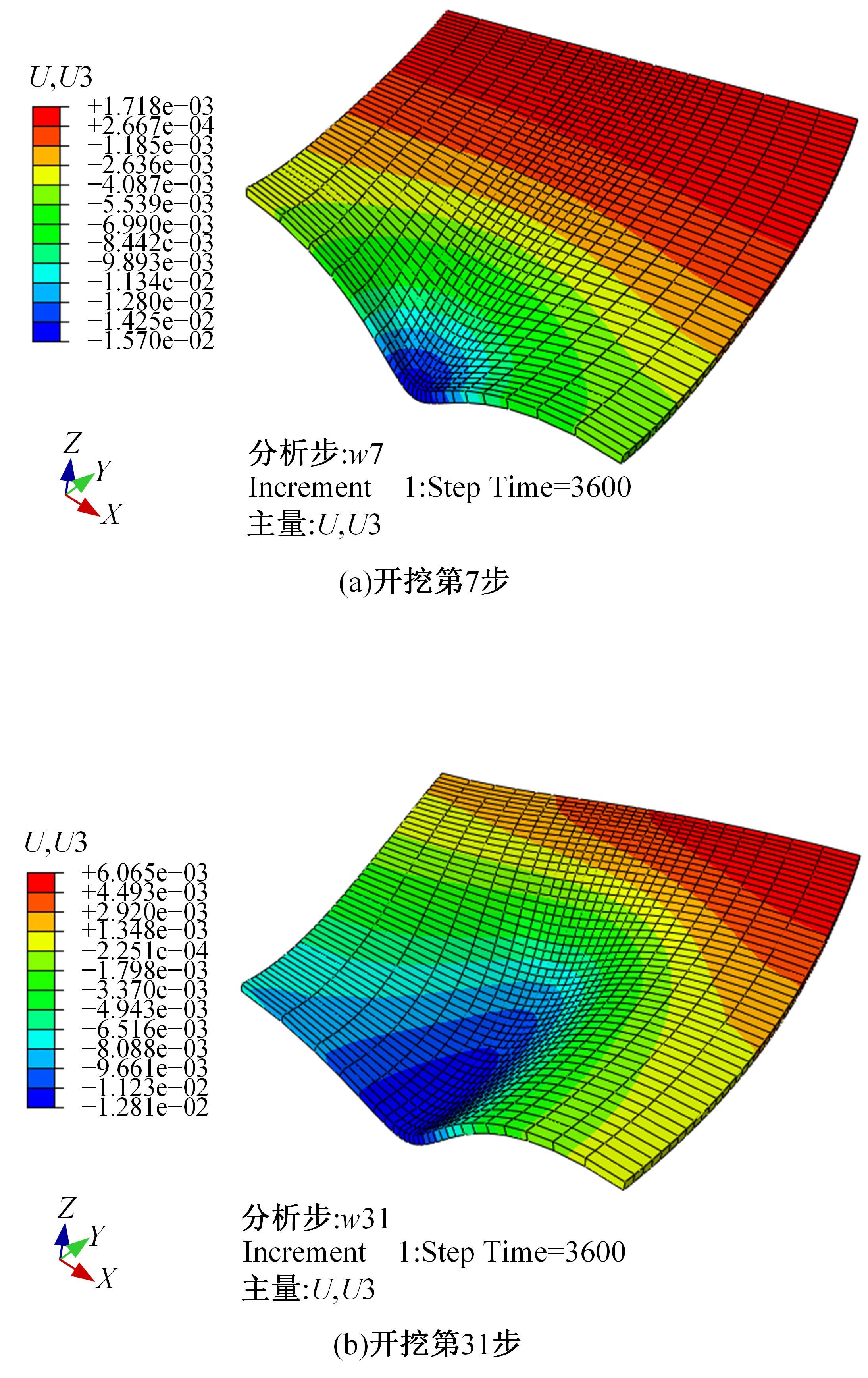
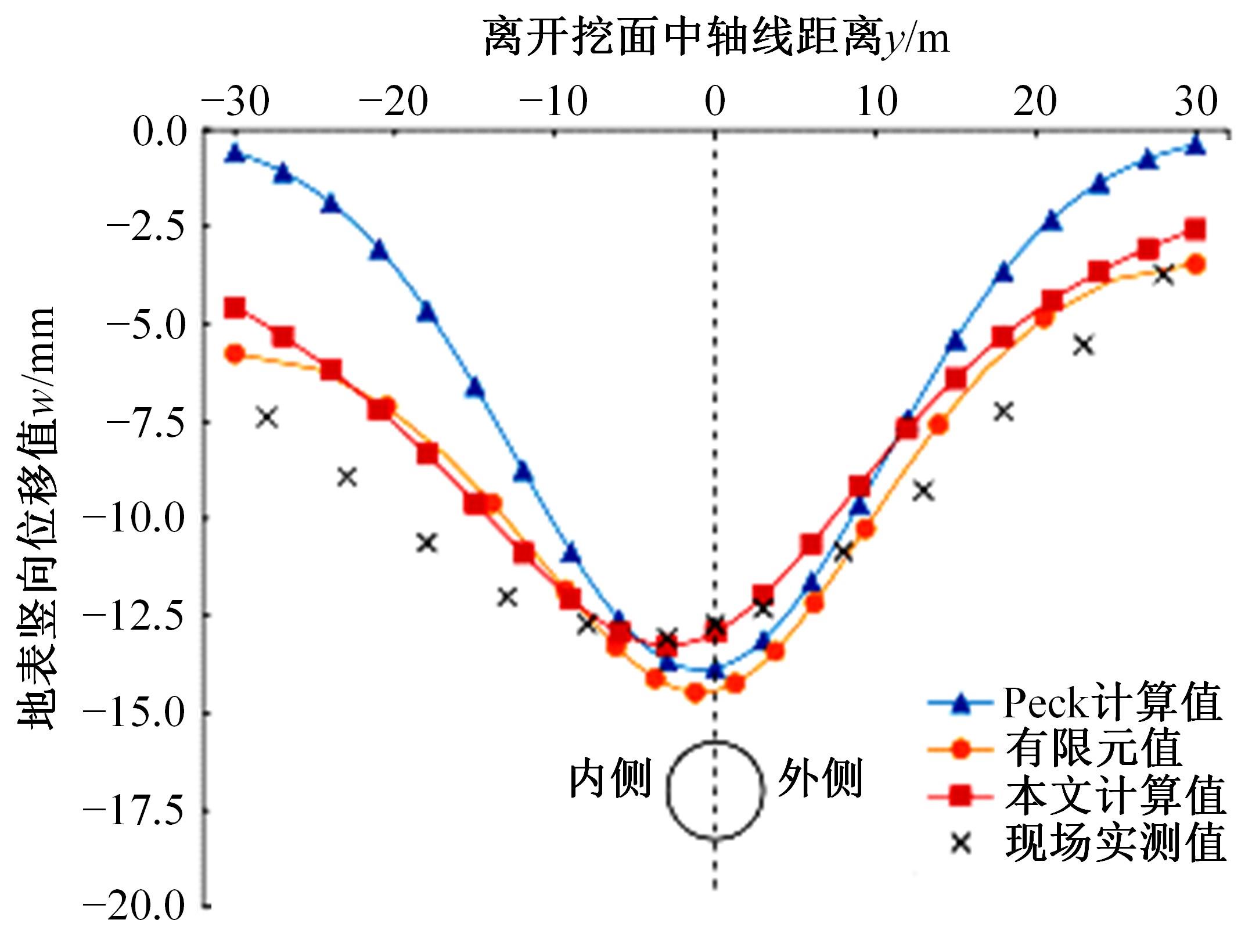
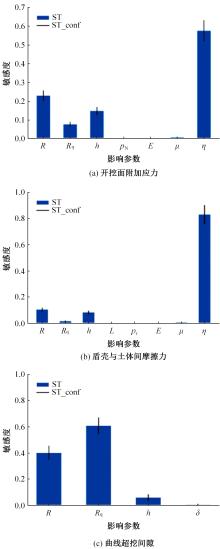
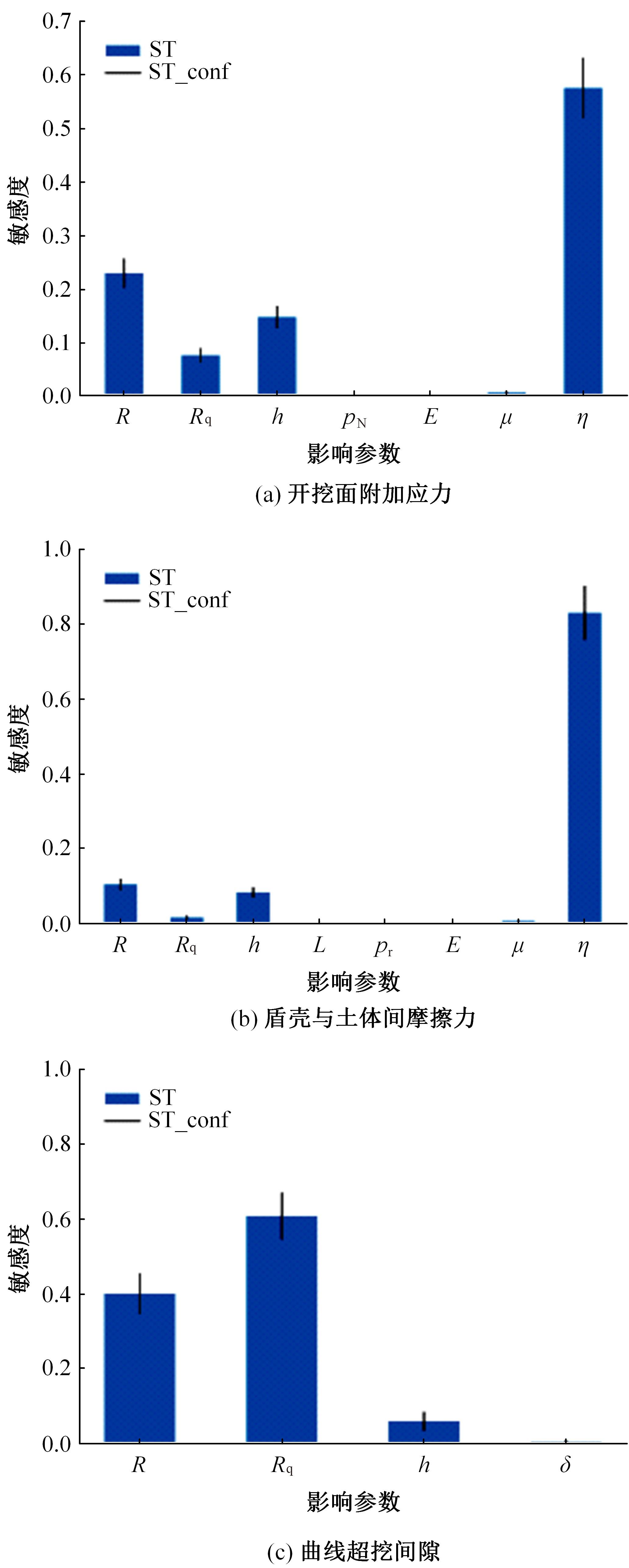
为了分析曲线盾构隧道施工期地表位移变化规律及影响因素，建立了考虑盾构主动铰接机构的曲线隧道开挖力学模型，分别提出了盾构施工附加应力和地层损失所引起的地表位移计算方法。基于实际工程，开展了相应监测试验和数值模拟，研究了影响地表位移偏移的敏感度指标。结果表明：曲线段地表位移沿隧道开挖方向向隧道内侧偏移，计算方法所得曲线段地表最大位移值和偏移值与实测值基本一致；敏感度分析发现，不平衡系数的敏感度最高，而在曲线超挖间隙因素中转弯半径和开挖半径敏感较高。建议曲线段施工应合理控制内外侧油缸推力差和超挖范围。

关键词: 盾构隧道, 地表位移, 计算方法, 曲线超挖间隙, 敏感度

Abstract:

To analyze the variation law and influencing factors of surface displacement during the construction of curved shield tunnel. The mechanical model of curved shield tunnel excavation considering active articulated mechanism is established， and the calculation methods of surface displacement caused by additional stress and ground loss based on mirror method and orifice expansion theory are deduced respectively. Based on the actual project， the corresponding monitoring test and numerical simulation are carried out， the sensitivity index affecting the surface displacement offset of curved shield was researched. The results show that： The surface displacement of the curved section is offset to the inside of the tunnel in the direction of tunnel excavation， and the maximum displacement value and offset value of the curved section obtained by the calculation method are basically consistent with the measured values. It is found that the sensitivity of the imbalance coefficient is the highest， while the turning radius and excavation radius are sensitive in the curve over-digging gap factor. It is recommended that the thrust difference and over-excavation range of the inner and outer cylinders should be reasonably controlled in the construction of the curve section.

Key words: shield tunnel, surface displacement, calculation method, curve over-digging gap, sensitivity

中图分类号:

TU456.3

杨果林,杨一凡,徐浩栋,罗桂军,肖洪波. 曲线盾构隧道施工期地表位移计算方法及影响因素分析[J]. 吉林大学学报(工学版), 2024, 54(7): 1997-2008.

Guo-lin YANG,Yi-fan YANG,Hao-dong XU,Gui-jun LUO,Hong-bo XIAO. Calculation method and influencing factors of surface displacement during construction of curved shield tunnel[J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(7): 1997-2008.

图/表 14

图1

图2

图3

图4

图5

图6

图7

图8

图9

图10

图11

图12

表1

图13

参考文献 20

1	梁宁慧,兰菲,庄炀,等. 城市地下综合管廊建设现状与存在问题[J]. 地下空间与工程学报,2020,16(6):1622-1635.
	Liang Ning-hui, Lan Fei, Zhuang Yang, et al. Current situation and existing problems of urban utility tunnel construction[J]. Chinese Journal of Underground Space and Engineering, 2020, 16(6): 1622-1635.
2	雷升祥,申艳军,肖清华,等. 城市地下空间开发利用现状及未来发展理念[J]. 地下空间与工程学报,2019,15(4):965-979.
	Lei Sheng-xiang, Shen Yan-jun, Xiao Qing-hua, et al. Present situations of development and utilization for underground space in cities and new viewpoints for future development[J]. Chinese Journal of Underground Space and Engineering, 2019, 15(4): 965-979.
3	魏纲,徐日庆. 软土隧道盾构法施工引起的纵向地面变形预测[J]. 岩土工程学报,2005,27(9):1077-1081.
	Wei Gang, Xu Ri-qing. Prediction of longitudinal ground deformation due to tunnel construction with shield in soft soil[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(9): 1077-1081.
4	魏纲,张世民,齐静静,等. 盾构隧道施工引起的地面变形计算方法研究[J]. 岩石力学与工程学报,2006,25():3317-3323.
	Wei Gang, Zhang Shi-min, Qi Jing-jing, et al. Study on calculation method of ground deformation induced by shield tunnel construction[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(Sup. 1): 3317-3323.
5	唐晓武,朱季,刘维,等. 盾构施工过程中的土体变形研究[J]. 岩石力学与工程学报,2010,29(2):417-422.
	Tang Xiao-wu, Zhu Ji, Liu Wei, et al. Research on soil deformation during shield construction process[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(2): 417-422.
6	卢海林,赵志民,方芃,等. 盾构法隧道施工引起土体位移与应力的镜像分析方法[J]. 岩土力学,2007,28(1): 45-50.
	Lu Hai-lin, Zhao Zhi-min, Fang Peng, et al. Analytical method of image theory used to calculate shield tunneling induced soil displacements and stresses[J]. Rock and Soil Mechanics, 2007, 28(1): 45-50.
7	宫亚峰,王博,魏海斌, 等. 基于Peck公式的双线盾构隧道地表沉降规律[J]. 吉林大学学报:工学版,2018,48(5):1411-1417.
	Gong Ya-feng, Wang Bo, Wei Hai-bin, et al. Surface subsidence law of double-line shield tunnel based on Peck formula[J]. Journal of Jilin University (Engineering and Technology Edition), 2018, 48(5): 1411-1417.
8	魏风冉,祝彦知,纠永志. 基于Mindlin解的盾构隧道地表沉降黏弹性分析[J]. 应用力学学报,2020,37(1):216-224, 483.
	Wei Feng-ran, Zhu Yan-zhi, Yong-zhi Jiu. Viscoelastic analysis of ground surface settlement of shield tunnel based on Mindlin solution[J]. Chinese Journal of Applied Mechanics, 2020, 37(1): 216-224, 483.
9	方勇,杨斌,杨志浩,等. 地铁盾构隧道施工对地层扰动的影响因素分析[J]. 重庆交通大学学报:自然科学版,2014,33(1):36-41.
	Fang Yong, Yang Bin, Yang Zhi-hao, et al. Influence of metro shield tunnel construction on ground disturbance[J]. Journal of Chongqing Jiaotong University(Natural Science), 2014, 33(1): 36-41.
10	刘招伟,王梦恕,董新平. 地铁隧道盾构法施工引起的地表沉降分析[J]. 岩石力学与工程学报,2003,22(8):1297-1301.
	Liu Zhao-wei, Wang Meng-shu, Dong Xin-ping. Analysis on ground surface subsidence of metro tunnel induced by shield construction[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(8): 1297-1301.
11	朱才辉,李宁. 隧道施工诱发地表沉降估算方法及其规律分析[J]. 岩土力学,2016,37():533-542.
	Zhu Cai-hui, Li Ning. Estimation method and laws analysis of surface settlement due to tunneling[J]. Rock and Soil Mechanics, 2016, 37(Sup.2): 533-542.
12	潘泓,苏文渊,翟国林,等. 小曲率半径转弯隧道盾构施工扰动实测分析[J]. 岩石力学与工程学报,2017,36(4):1024-1031.
	Pan Hong, Su Wen-yuan, Zhai Guo-lin, et al. Soil disturbance induced by shield advancing through a small radius path[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(4): 1024-1031.
13	孙捷城,路林海,王国富,等. 小半径曲线盾构隧道掘进施工地表变形计算[J]. 中国铁道科学,2019,40(5):63-72.
	Sun Jie-cheng, Lu Lin-hai, Wang Guo-fu, et al. Calculation method of surface deformation induced by small radius curve shield tunneling construction[J]. China Railway Science, 2019, 40(5): 63-72.
14	邓皇适,傅鹤林,史越. 小转弯半径曲线盾构隧道开挖引发地表沉降计算[J]. 岩土工程学报,2021,43(1): 165-173.
	Deng Huang-shi, Fu He-lin, Shi Yue. Calculation of surface settlement caused by excavation of shield tunnels with small turning radius[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(1): 165-173.
15	Mindlin R D. Force at a point in the interior of a semi-infinite solid[J]. Physics, 1936, 7(5): 195-201.
16	Sagaseta C. Analysis of undrained soil deformation due to ground loss[J]. Geotechnique, 1987, 37(3):301-320.
17	Lee K M, Rowe R K, Lo K Y. Subsidence owing to tunneling, I: estimating the gap parameter[J]. Canadian Geotechnical Journal, 1992, 6(29): 929-940.
18	张冠茂. 多重复化高斯—勒让德积分公式及其应用[J]. 兰州大学学报:自然科学版,2000,36(5):30-34.
	Zhang Guan-mao. Multiple-complex-gauss-legendre integral formulae and application[J]. Journal of Lanzhou University(Natural Sciences), 2000, 36(5): 30-34.
19	郝晓龙. 小半径曲线地铁盾构施工地面沉降分析[D].石家庄: 石家庄铁道大学土木工程学院, 2020.
	Hao Xiao-long. Ground settlement of small radius curve subway induced by shield construction[D]. Shijiazhuang:School of Civil Engineering, Shijiazhuang Tiedao University, 2020.
20	刘松,佘敦先,张利平,等. 基于Morris和Sobol的水文模型参数敏感性分析[J].长江流域资源与环境, 2019, 28(6):1296-1303.
	Liu Song, She Dun-xian, Zhang Li-ping, et al. Global sensitivity analysis of hydrological model parameters based on morris and sobol methods[J]. Resources and Environment in the Yangtze Basin, 2019, 28(6): 1296-1303.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

名称	实测值	Peck方法	有限元法	本文方法
最大位移/mm	13.07	13.89	14.47	13.25
偏差比例	/	6.27%	10.71%	1.38%
偏移值/m	3	1	1.25	3
偏差比例	/	66.67%	58.33	0

[1]	陈城,史培新,贾鹏蛟,董曼曼. 基于MK-LSTM算法的盾构掘进参数相关性分析及结构变形预测[J]. 吉林大学学报(工学版), 2024, 54(6): 1624-1633.
[2]	黄汉辉,陈康明,吴庆雄. 钢管混凝土桁式弦杆组合连续梁抗弯性能[J]. 吉林大学学报(工学版), 2024, 54(6): 1665-1676.
[3]	章子玲,胡雄,亓寅,王微,陶志强,刘志峰. 基于向量投影响应面的数控机床几何误差分配方法[J]. 吉林大学学报(工学版), 2022, 52(2): 384-391.
[4]	王杨,宋占帅,郭孔辉,庄晔. 转动惯量试验台的惯性参数测量[J]. 吉林大学学报(工学版), 2019, 49(6): 1795-1801.
[5]	陈东辉, 吕建华, 龙刚, 张宇晨, 常志勇. 基于ADAMS的半悬挂式农业机组静侧翻稳定性[J]. 吉林大学学报(工学版), 2018, 48(4): 1176-1183.
[6]	孙晓颖, 扈泽正, 杨锦鹏. 基于分层贝叶斯网络的车辆发动机系统电磁脉冲敏感度评估[J]. 吉林大学学报(工学版), 2018, 48(4): 1254-1264.
[7]	孙晓颖, 王震, 杨锦鹏, 扈泽正, 陈建. 基于贝叶斯网络的电子节气门电磁敏感度评估[J]. 吉林大学学报(工学版), 2018, 48(1): 281-289.
[8]	高印寒, 安占扬, 王举贤, 王天皓, 刘长英, 张俊东. 等效线束法在汽车线束时域辐射敏感度分析中的应用[J]. 吉林大学学报(工学版), 2015, 45(3): 946-952.
[9]	蔡朝晖, 张健沛, 杨静. 基于贝叶斯网络的路网位置匿名区域估计[J]. 吉林大学学报(工学版), 2014, 44(2): 454-458.
[10]	周伟, 赵胜川. 基于Mixed Logit模型的路线选择行为量化分析[J]. 吉林大学学报(工学版), 2013, 43(02): 304-309.
[11]	郭睿，陈塑寰，孟广伟 . 特征值高阶灵敏度的有效算法[J]. 吉林大学学报(工学版), 2008, 38(增刊): 132-0136.
[12]	高印寒，马喜来，陈如娜. 基于模糊推理的汽车电磁兼容预测技术[J]. 吉林大学学报(工学版), 2006, 36(03): 399-0403.