钢管混凝土桁式弦杆组合连续梁抗弯性能

doi:10.13229/j.cnki.jdxbgxb.20221039

摘要/Abstract

摘要：

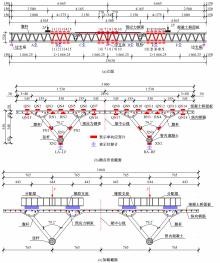
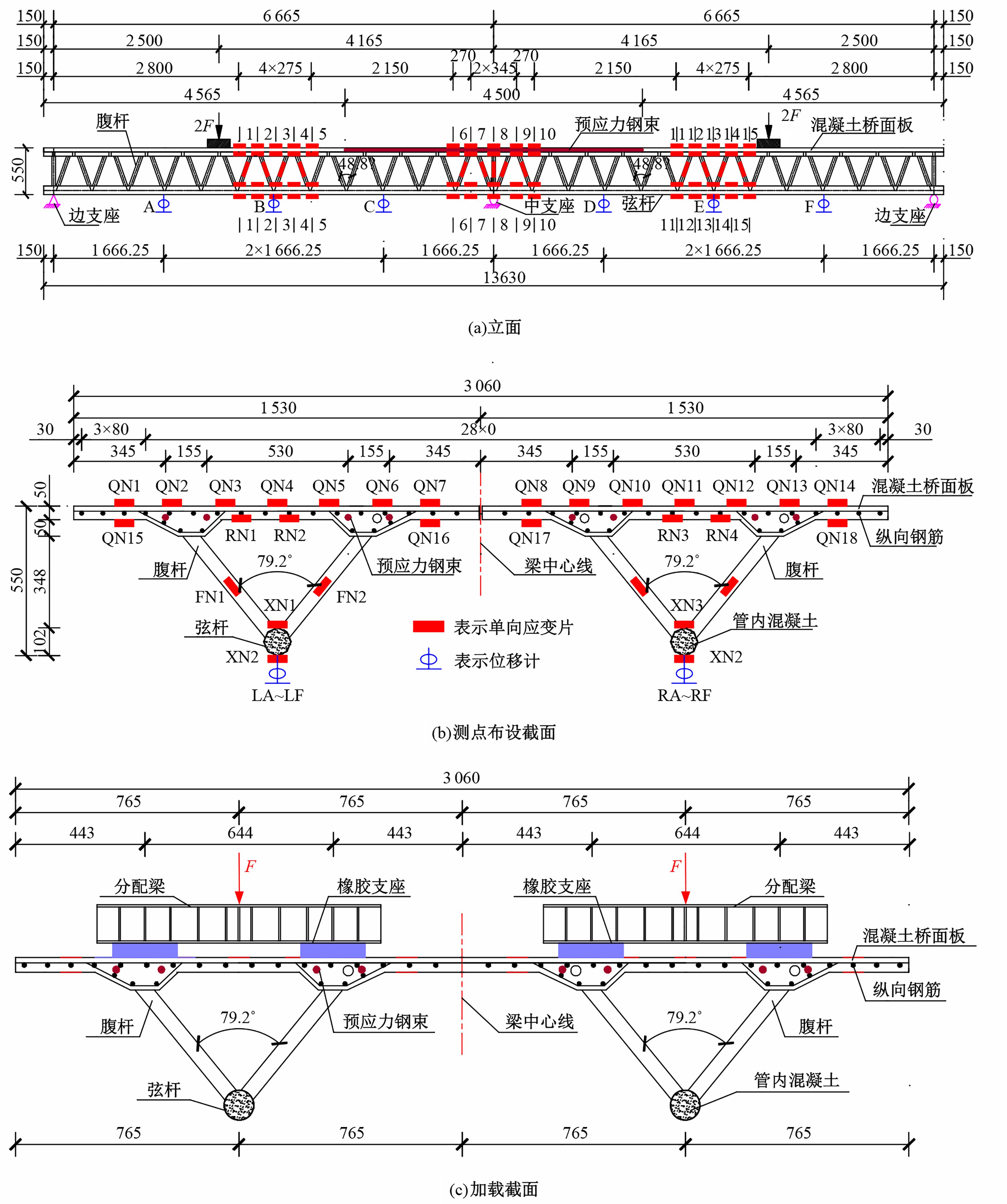
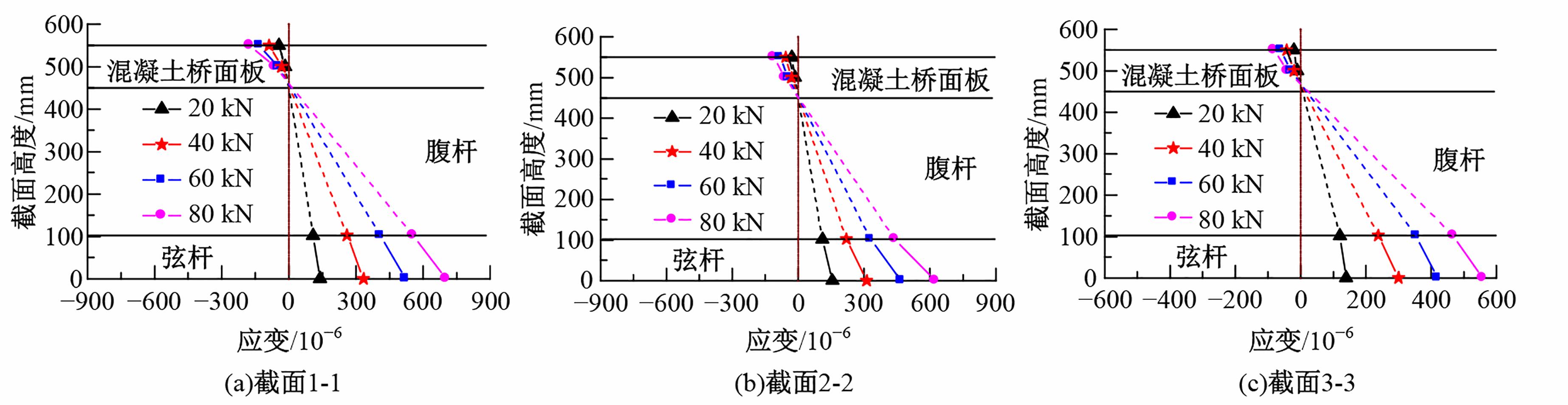
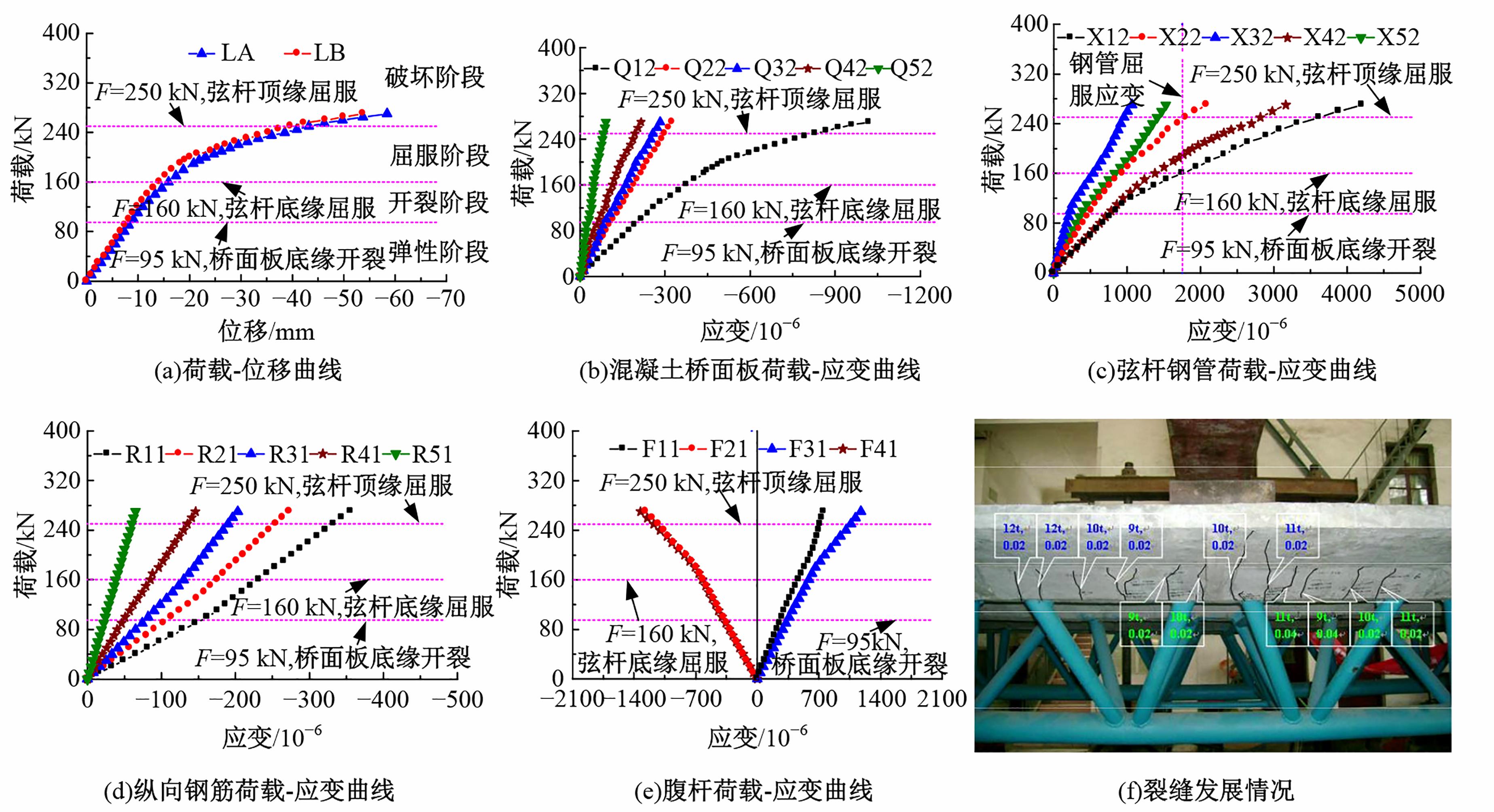
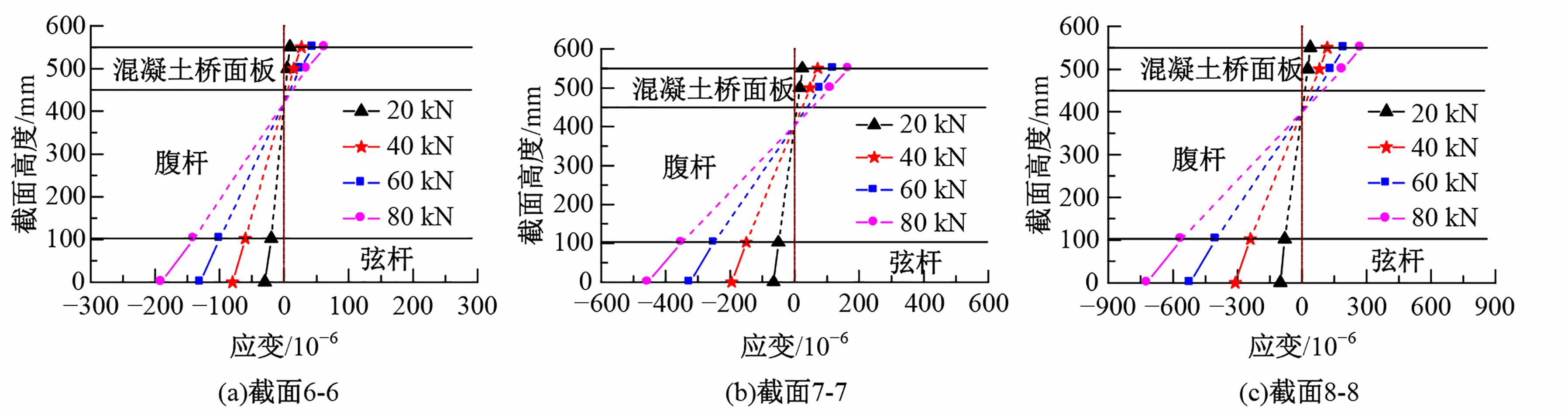
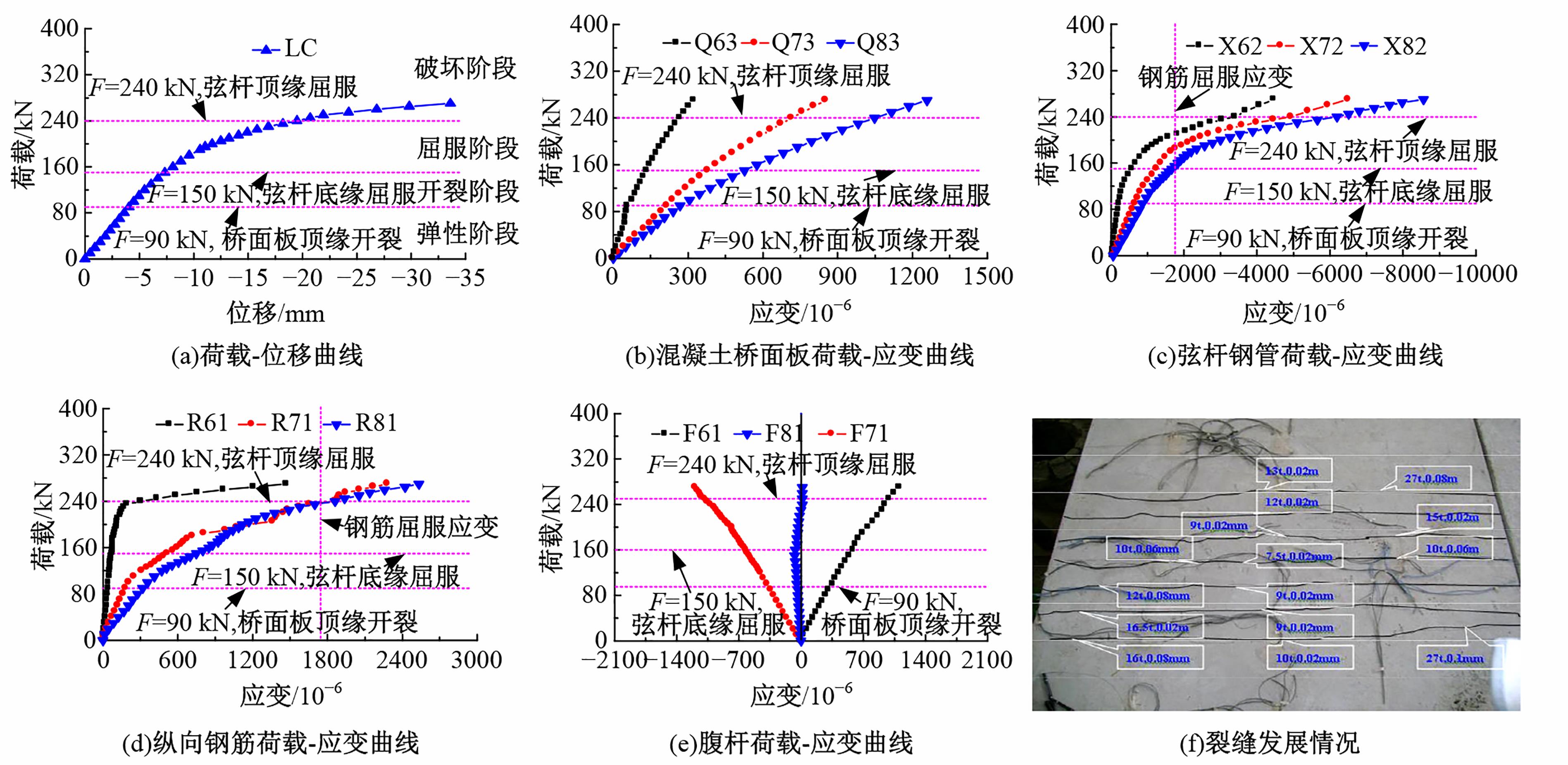
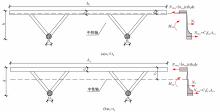
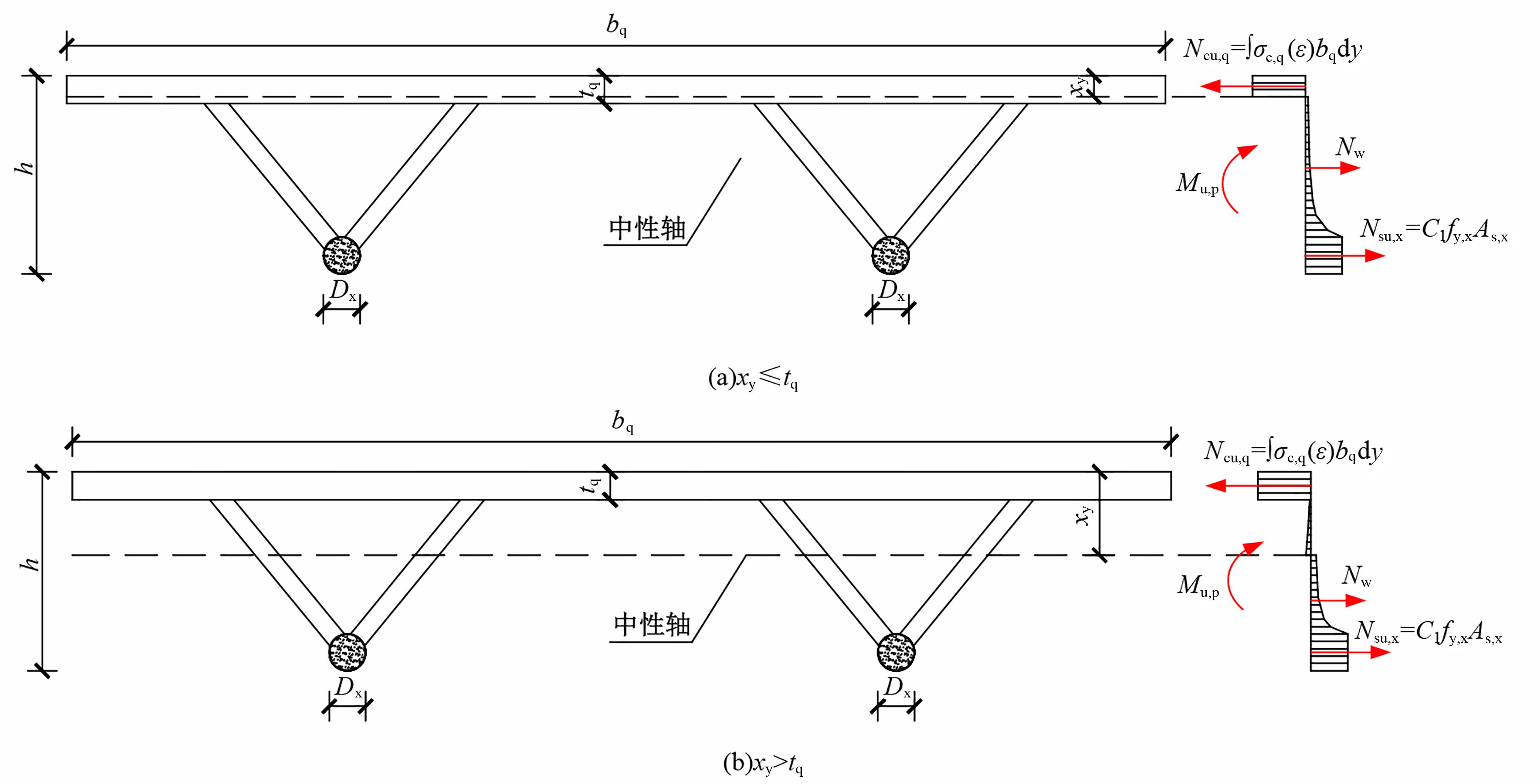
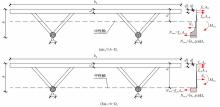
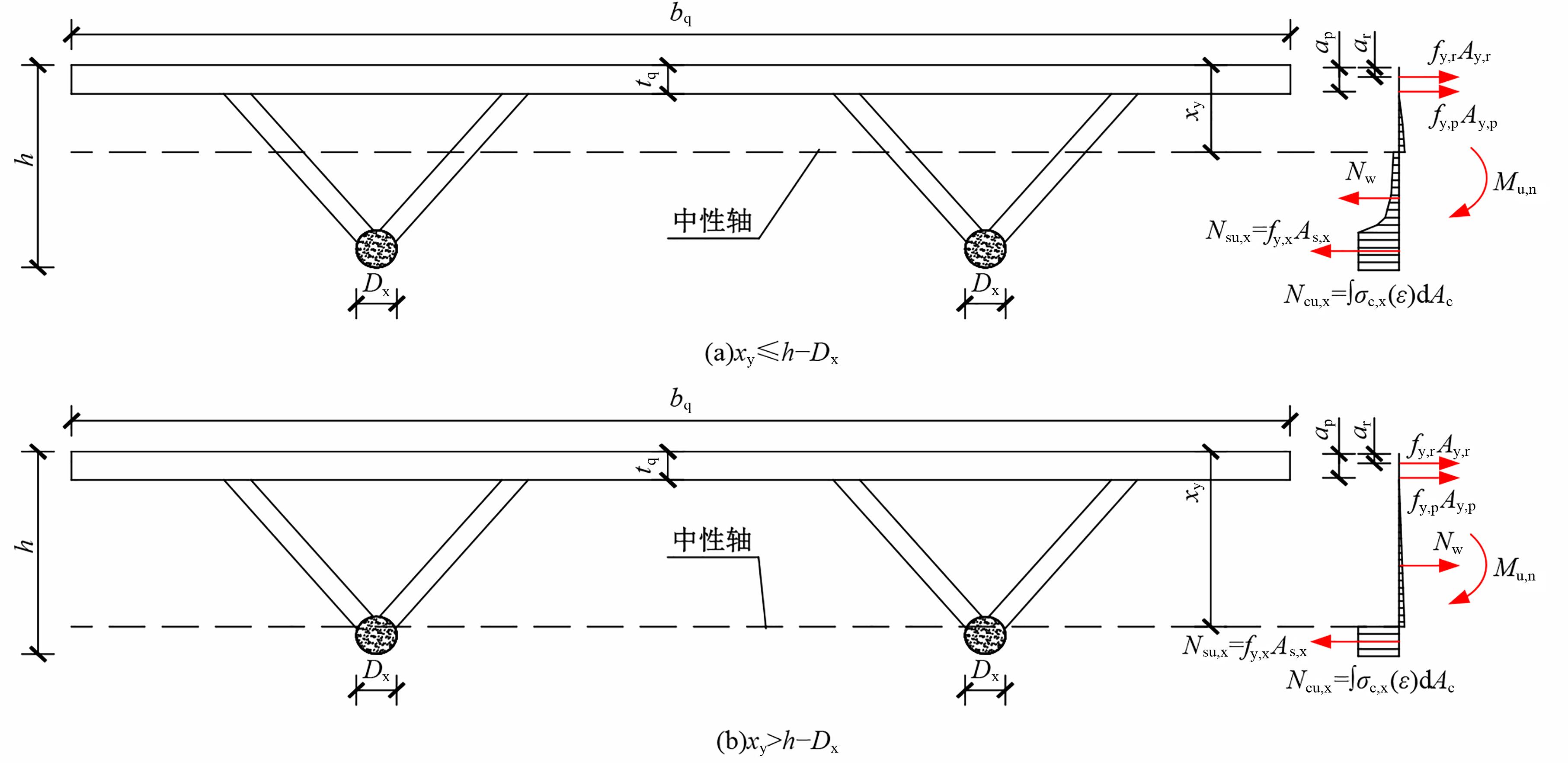
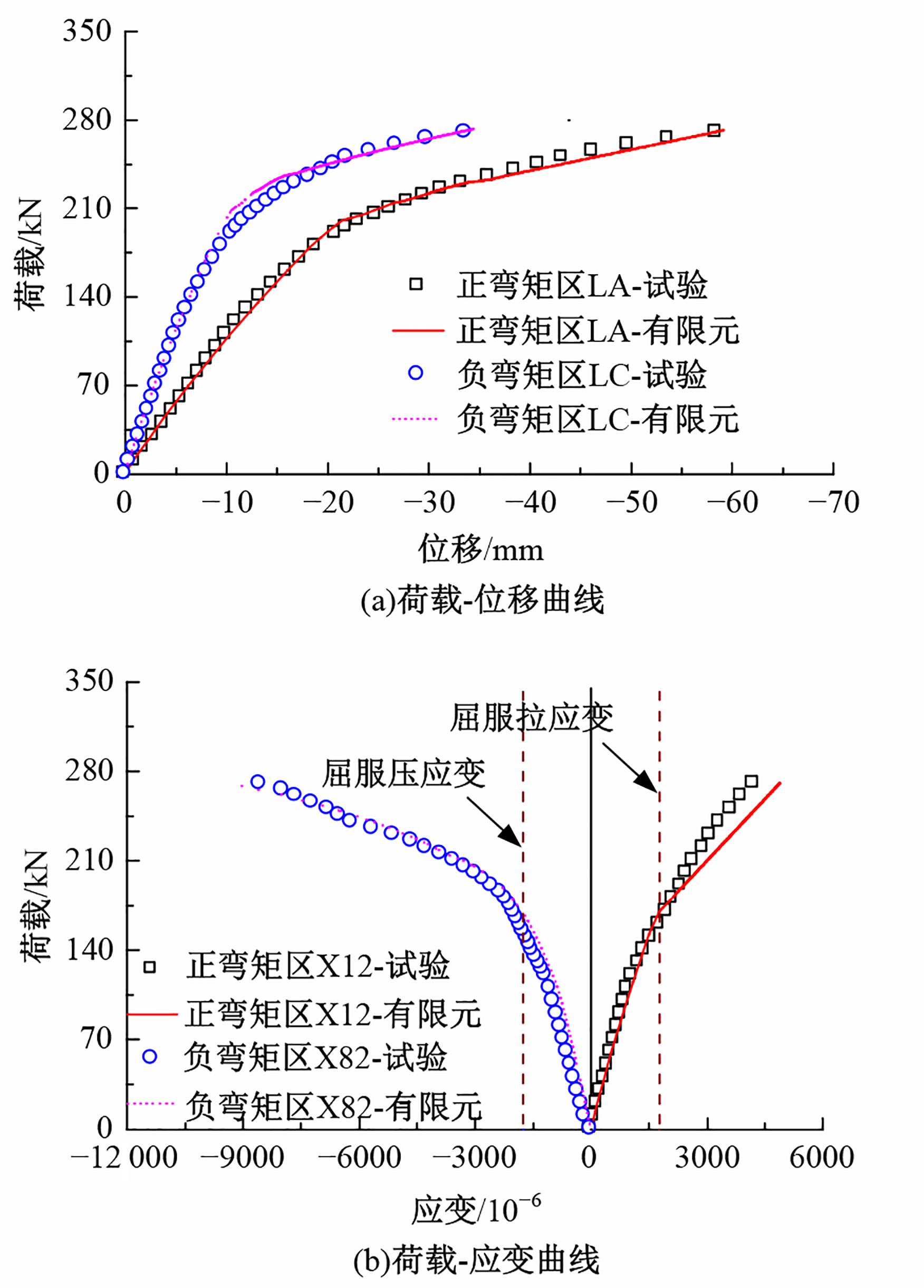
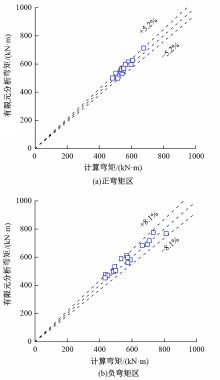
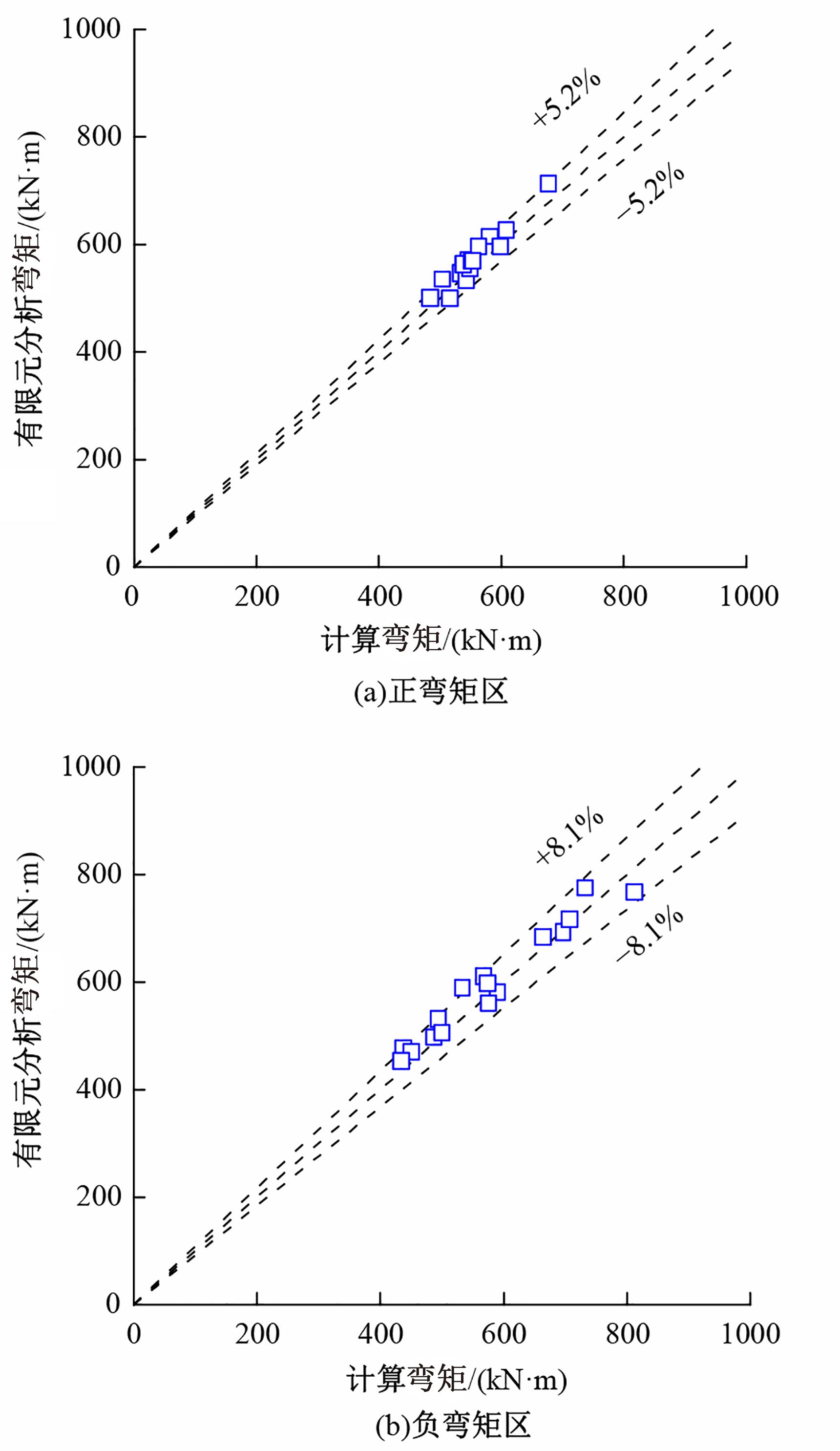
为研究钢管混凝土桁式弦杆组合连续梁的抗弯性能和计算方法，开展了模型试验和理论分析，研究钢管混凝土桁式弦杆组合连续梁正、负弯矩区的应变分布、变形特性、破坏形态和抗弯承载能力，并对正、负弯矩区的抗弯承载能力计算方法进行讨论。结果表明：钢管混凝土桁式弦杆组合连续梁正、负弯矩区的腹杆和节点均具有较高的强度和刚度，能够保证节点破坏不会先于截面整体破坏。截面应变沿高度方向基本呈线性变化，满足平截面假定。正、负弯矩区的抗弯承载能力破坏形态分别是弦杆钢管全截面屈服和混凝土桥面板内部钢筋发生屈服。腹杆对钢管混凝土桁式弦杆组合连续梁正、负弯矩区抗弯承载能力的贡献度分别为12.5%和8.6%。本文提出了考虑腹杆贡献的钢管混凝土桁式弦杆组合连续梁抗弯承载能力的计算方法，其计算结果与试验和有限元分析结果进行对比分析，误差不超过8.1%。

关键词: 桥梁工程, 组合连续梁, 钢管混凝土桁式弦杆, 抗弯性能, 模型试验, 理论分析, 计算方法

Abstract:

To study the flexural behavior and the calculation method of composite continuous girders with concrete-filled steel tubular （CFST） truss chords， model tests and theoretical analysis were carried out. The strain distribution， deformation property， failure mode， flexural bearing capacity of both the positive and negative bending moment area of composite continuous girders with CFST truss chords were studied. The calculation method for the flexural bearing capacity for both the positive and negative bending moment area was also discussed. The brace and the joint in the positive and negative bending moment area of composite continuous girders with CFST truss chords has higher strength and stiffness， and it can make sure that the failure of the joint is not prior to that of the whole section. The strain changes linearly along the depth direction of the cross section， and it meets the plane-section assumption. The flexural bearing capacity failure mode of the positive and negative bending moment area are that the full cross section of the chord and the rebar used in the concrete bridge deck slab yield， respectively. The contributions of the web members to the flexural bearing capacity in the positive and negative bending moment area of composite continuous girders with CFST truss chords are 12.5% and 8.6%， respectively. The calculation method considering the contributions of the web members to the flexural bearing capacity for composite continuous girders with CFST truss chords is put forward. The deviation between the result acquired by the calculation method for the flexural bearing capacity above and that acquired by the test and finite element analysis is less than 8.1%.

Key words: bridge engineering, composite continuous girders, concrete-filled steel tubular truss chords, flexural behavior, model test, theoretical analysis, calculation method

中图分类号:

U441

黄汉辉,陈康明,吴庆雄. 钢管混凝土桁式弦杆组合连续梁抗弯性能[J]. 吉林大学学报(工学版), 2024, 54(6): 1665-1676.

Han-hui HUANG,Kang-ming CHEN,Qing-xiong WU. Flexural behavior of composite continuous girders with concrete-filled steel tubular truss chords[J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(6): 1665-1676.

图/表 13

图1

表 1

图 2

图3

图4

图5

图6

图7

图8

表 2

图9

表3

图10

参考文献 29

1	Jung K H, Kim J H J, Yi J W, et al. Development and evaluation of new connection systems for hybrid truss bridges[J]. Journal of Advanced Concrete Technology, 2013, 11(2): 61-79.
2	Tian Z J, Liu Y J, Jiang L, et al. A review on application of composite truss bridges composed of hollow structural section members[J]. Journal of Traffic and Transportation Engineering (English Edition), 2019, 6(1): 94-108.
3	Xu F, Chen J, Chan T M. Mechanical behaviour of concrete-filled CHS connections subjected to in-plane bending[J]. Engineering Structures, 2017, 148: 101-112.
4	Song S S, Chen J, Xu F. Mechanical behaviour and design of concrete-filled K and KK CHS connections [J]. Journal of Constructional Steel Research, 2022, 188: 107000.
5	Hou C, Han L H, Mu T M. Behaviour of CFDST chord to CHS brace composite K-joints: experiments [J]. Journal of Constructional Steel Research, 2017, 135: 97-109.
6	Xie K Z, Wang H W, Pang J H, et al. Study of the ultimate bearing capacity of concrete-filled steel tube K-joints[J]. KSCE Journal of Civil Engineering, 2019, 23(5): 2254-2262.
7	Xu F, Chen J, Jin W L. Punching shear failure of concrete-filled steel tubular CHS connections[J]. Journal of Constructional Steel Research, 2016, 124: 113-121.
8	Xu F, Chen J, Jin W L. Experimental investigation of SCF distribution for thin-walled concrete-filled CHS joints under axial tension loading[J]. Thin-walled Structures, 2015, 93: 149-157.
9	Wei X, Wen Z Y, Xiao L, et al. Review of fatigue assessment approaches for tubular joints in CFST trusses[J]. International Journal of Fatigue, 2018, 113: 43-53.
10	Tong L W, Chen K P, Xu G W, et al. Formulae for hot-spot stress concentration factors of concrete-filled CHS T-joints based on experiments and FE analysis [J]. Thin-walled Structures, 2019, 136: 113-128.
11	Huang W J, Fenu L, Chen B C, et al. Experimental study on K-joints of concrete-filled steel tubular truss structures[J]. Journal of Constructional Steel Research, 2015, 107: 182-193.
12	Zheng J, Nakamura S, Ge Y J, et al. Extended formulation of stress concentration factors for CFST T-joints[J]. Journal of Bridge Engineering, 2020, 25(1): 06019006.
13	Zheng J, Nakamura S, Okumatsu T, et al. Formulation of stress concentration factors for concrete-filled steel tubular (CFST) K-joints under three loading conditions without shear forces[J]. Engineering Structures, 2019, 190: 90-100.
14	Musa I A, Mashiri F R. Stress concentration factor in concrete-filled steel tubular K-joints under balanced axial load[J]. Thin-walled Structures, 2019, 139: 186-195.
15	Hou C, Han L H, Mu T M, et al. Analytical behaviour of CFST chord to CHS brace truss under flexural loading[J]. Journal of Constructional Steel Research, 2017, 134: 66-79.
16	Huang W J, Fenu L, Chen B C, et al. Experimental study on joint resistance and failure modes of concrete filled steel tubular (CFST) truss girders[J]. Journal of Constructional Steel Research, 2018, 141: 241-250.
17	Han L H, Xu W, He S H, et al. Flexural behaviour of concrete filled steel tubular (CFST) chord to hollow tubular brace truss: experiments[J]. Journal of Constructional Steel Research, 2015, 109: 137-151.
18	Huang Y H, Liu A R, Fu J Y, et al. Experimental investigation of the flexural behavior of CFST trusses with interfacial imperfection[J]. Journal of Constructional Steel Research, 2017, 137: 52-65.
19	Zhou W B, Chen Y, Wang K, et al. Experimental research on circular concrete filled stainless steel tubular truss[J]. Thin-walled Structures, 2017, 117: 224-238.
20	Chen Y, Feng R, Gao S W. Experimental study of concrete-filled multiplanar circular hollow section tubular trusses[J]. Thin-walled Structures, 2015, 94: 199-213.
21	Xu W, Han L H, Tao Z. Flexural behaviour of curved concrete filled steel tubular trusses[J]. Journal of Constructional Steel Research, 2014, 93: 119-134.
22	Chen S L, Hou C, Zhang H, et al. Structural behaviour and reliability of CFST trusses with random initial imperfections[J]. Thin-walled Structures, 2019, 143: 106192.
23	. 混凝土物理力学性能试验方法标准 [S].
24	. 金属材料拉伸试验第1部分: 室温试验方法 [S].
25	曾明根, 武彧, 苏庆田. 钢纤维混凝土组合桥面板负弯矩区开裂性能试验[J]. 吉林大学学报:工学版, 2023, 53(11): 3176-3185.
	Zeng Ming-gen, Wu Yu, Su Qing-tian. Experimental studies on cracking behavior of steel fiber reinforced concrete slab in negative moment region of orthotropic composite bridge deck[J]. Journal of Jilin University (Engineering and Technology Edition), 2023, 53(11): 3176-3185.
26	. 混凝土结构设计规范 [S].
27	刘威. 钢管混凝土局部受压时的工作机理研究[D]. 福州: 福州大学土木工程学院, 2005.
	Liu Wei. Research on mechanism of concrete-filled steel tubes subjected to local compression[D]. Fuzhou: College of Civil Engineering, Fuzhou University, 2005.
28	王彤, 谢旭, 王渊, 等. 桁腹式组合桁梁结构计算理论[J]. 浙江大学学报:工学版, 2014, 48(4): 711-720.
	Wang Tong, Xie Xu, Wang Yuan, et al. Analysis of prestressed composite truss girders with steel truss webs[J]. Journal of Zhejiang University (Engineering Science), 2014, 48(4): 711-720.
29	. 钢管混凝土结构技术规范 [S].

相关文章 15

[1]	张春雷,邵长宇,苏庆田,戴昌源. 球扁钢肋钢纤维混凝土组合桥面板正弯矩受力性能试验[J]. 吉林大学学报(工学版), 2024, 54(6): 1634-1642.
[2]	邵长江,崔皓蒙,漆启明,庄卫林. 近断层大跨RC轻柔拱桥纵向阻尼器减震研究[J]. 吉林大学学报(工学版), 2024, 54(5): 1355-1367.
[3]	赵秋,陈鹏,赵煜炜,余澳. 台后设置拱形结构的无缝桥梁整体受力性能[J]. 吉林大学学报(工学版), 2024, 54(4): 1016-1027.
[4]	张洪,朱志伟,胡天宇,龚燕峰,周建庭. 基于改进YOLOv5s的桥梁螺栓缺陷识别方法[J]. 吉林大学学报(工学版), 2024, 54(3): 749-760.
[5]	韩智强,谢刚,卓亚娟,骆佐龙,李华腾. 基于车轮-桥面相干激励的大跨连续梁桥振动响应[J]. 吉林大学学报(工学版), 2024, 54(2): 436-444.
[6]	杨国俊,齐亚辉,石秀名. 基于数字图像技术的桥梁裂缝检测综述[J]. 吉林大学学报(工学版), 2024, 54(2): 313-332.
[7]	谭国金,欧吉,艾永明,杨润超. 基于改进DeepLabv3+模型的桥梁裂缝图像分割方法[J]. 吉林大学学报(工学版), 2024, 54(1): 173-179.
[8]	龙关旭,张修石,辛公锋,王涛,杨干. 融合机器视觉的桥梁动态称重方法[J]. 吉林大学学报(工学版), 2024, 54(1): 188-197.
[9]	卫星,高亚杰,康志锐,刘宇辰,赵骏铭,肖林. 低温环境下栓钉环焊缝焊接残余应力场数值模拟[J]. 吉林大学学报(工学版), 2024, 54(1): 198-208.
[10]	安然,王有志. 剪力钉连接件拉剪共同作用抗剪性能[J]. 吉林大学学报(工学版), 2023, 53(9): 2554-2562.
[11]	左新黛,张劲泉,赵尚传. 在役混凝土T梁疲劳刚度退化及寿命预测方法[J]. 吉林大学学报(工学版), 2023, 53(9): 2563-2572.
[12]	顾正伟,张攀,吕东冶,吴春利,杨忠,谭国金,黄晓明. 基于数值仿真的简支梁桥震致残余位移分析[J]. 吉林大学学报(工学版), 2023, 53(6): 1711-1718.
[13]	吴春利,黄诗茗,李魁,顾正伟,黄晓明,张炳涛,杨润超. 基于数值仿真和统计分析的洪水作用下桥墩作用效应分析[J]. 吉林大学学报(工学版), 2023, 53(6): 1612-1620.
[14]	谭国金,孔庆雯,何昕,张攀,杨润超,朝阳军,杨忠. 基于动力特性和改进粒子群优化算法的桥梁冲刷深度识别[J]. 吉林大学学报(工学版), 2023, 53(6): 1592-1600.
[15]	江辉,李新,白晓宇. 桥梁抗震结构体系发展述评：从延性到韧性[J]. 吉林大学学报(工学版), 2023, 53(6): 1550-1565.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

材料	部件	弹性模量/MPa	抗压强度/MPa	屈服强度/MPa	极限抗拉强度/MPa	泊松比
混凝土	桥面板	39 600	52.7	—	—	0.2
混凝土	管内混凝土	27 100	37.1	—	—	0.2
钢结构	弦杆钢管	200 000	—	351	501	0.3
	腹杆	200 000	—	314	483	0.3
	纵向钢筋	204 000	—	356	464	0.3

来源	正弯矩区/（kN·m）	正弯矩区/（kN·m）
试验	580.2	513.6
计算值	549.9	498.4
计算值/试验	0.948	0.970

部件	参数取值
腹杆径厚比	10	12	14	16
弦杆径厚比	22.5	25.0	27.5	30.0
高跨比	1/10	1/11	1/12	1/13
腹杆轴线间夹角/（°）	35	40	45	50