吉林大学学报(工学版) ›› 2024, Vol. 54 ›› Issue (7): 2038-2048.doi: 10.13229/j.cnki.jdxbgxb.20221161
• 计算机科学与技术 • 上一篇
基于JS散度的不确定数据密度峰值聚类算法
- 1.哈尔滨理工大学 计算机科学与技术学院,哈尔滨 150080
2.奇安信科技集团股份有限公司 战略研究部,北京 100088
Peak clustering algorithm for uncertain data density based on JS divergence
Song LI1( ),Xiao-nan LIU1,Juan LIU2
),Xiao-nan LIU1,Juan LIU2
- 1.School of Computer Science and Technology,Harbin University of Science and Technology,Harbin 150080,China
2.Strategic Research,Qi An Xin Technology Group Inc,Beijing 100088,China
摘要:
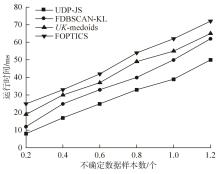
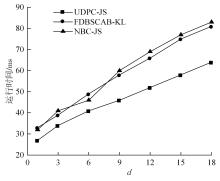
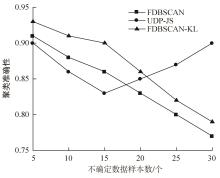
针对传统的基于密度的不确定性聚类算法存在参数敏感和对复杂流形不确定数据集得到聚类结果较差的缺陷,提出一种新的基于JS散度的不确定数据密度峰值聚类算法(UDPC-JS)。该算法首先用不确定自然邻居定义的不确定自然邻域密度因子去除噪声点;其次,通过不确定自然邻居和JS散度相结合的方式计算不确定数据对象的局部密度,通过结合代表点的思想找到不确定数据集的初始聚类中心,并在初始聚类中心之间定义基于JS散度和图的距离;然后,再利用基于不确定自然邻居和JS散度计算出的局部密度和在初始聚类中心之间新定义的基于JS散度和图的距离在初始聚类中心上构建决策图,并根据决策图选择最终的聚类中心;最后,将未分配的不确定数据对象分配到其初始聚类中心所在的簇中。实验结果表明:该算法较对比算法具有更好的聚类效果和准确性,并且在处理复杂流形的不确定数据集上的优势较大。
中图分类号:
- TP311
| 1 | 李松, 王冠群, 郝晓红, 等. 面向推荐系统的多目标决策优化算法[J].西安交通大学学报, 2022, 56(8):104-112. |
| Li Song, Wang Guan-qun, Hao Xiao-hong, et al. A multi-objective decision optimization algorithm for recommendation system[J]. Journal of Xi´an Jiao Tong University, 2022, 56(8):104-112. | |
| 2 | Khan S S, Ahmad A. Cluster center initialization algorithm for K-means clustering[J]. Pattern Recognition Letters, 2004, 25(11): 1293-1302. |
| 3 | Chau M, Cheng R, Kao B, et al. Uncertain data mining: an example in clustering location data[C]∥ Pacific-Asia Conference on Knowledge Discovery and Data Mining. Berlin:Springer, 2006: 199-204. |
| 4 | Kaufman L, Rousseeuw P J. An Introduction to Cluster Analysis[M]. London:John Wiley and Sons, Incorporated, 1990. |
| 5 | Gullo F, Ponti G, Tagarelli A. Clustering uncertain data via k-medoids[C]∥Proceedings of the 2nd international conference on Scalable Uncertainty Management, Berlin,Germany,2008: 229-242. |
| 6 | Tran L, Duckstein L. Comparison of fuzzy numbers using a fuzzy distance measure[J]. Fuzzy Sets and Systems, 2002, 130(3): 331-341. |
| 7 | Ester M, Kriegel H P, Sander J, et al. A density-based algorithm for discovering clusters in large spatial databases with noise[C]∥The 2nd International Conference on Knowledge Discovery and Data Mining, Portland,USA,1996: 226-231. |
| 8 | Kriegel H P, Pfeifle M. Hierarchical density-based clustering of uncertain data[C]∥Fifth IEEE International Conference on Data Mining,Houston, USA,2005: 672-677. |
| 9 | Ankerst M, Breunig M M, Kriegel H P, et al. OPTICS: ordering points to identify the clustering structure[J]. ACM Sigmod record, 1999, 28(2): 49-60. |
| 10 | Liu H, Zhang X, Zhang X, et al. Self-adapted mixture distance measure for clustering uncertain data[J]. Knowledge-Based Systems, 2017, 126: 33-47. |
| 11 | Rodriguez A, Laio A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492-1496. |
| 12 | Ni L, Luo W, Bu C, et al. Improved CFDP algorithms based on shared nearest neighbors and transitive closure[C]∥Pacific-Asia Conference on Knowledge Discovery and Data Mining,Tokyo, Japan, 2017: 79-93. |
| 13 | Guo Z, Huang T, Cai Z, et al. A new local density for density peak clustering[C]∥Pacific-Asia Conference on Knowledge Discovery and Data Mining,Tokyo, Japan,2018: 426-438. |
| 14 | 纪霞, 姚晟, 赵鹏. 相对邻域与剪枝策略优化的密度峰值聚类算法[J]. 自动化学报, 2019, 45(4): 1-14. |
| Ji Xia, Yao Sheng, Zhao Peng. Density peak clustering algorithm optimized by relative neighborhood and pruning strategy[J]. Acta Automation Sinica, 2019, 45(4): 1-14. | |
| 15 | Wu Y, He Y, Huang J Z.Clustering ensembles based on probability density function estimation[C]∥The 7th IEEE International Conference on Cyber Security and Cloud Computing (CSCloud)/The 6th IEEE International Conference on Edge Computing and Scalable Cloud (EdgeCom), New York,USA,2020 : 126-131. |
| 16 | Yang L, Bi S, Faes M G R, et al. Bayesian inversion for imprecise probabilistic models using a novel entropy-based uncertainty quantification metric[J]. Mechanical Systems and Signal Processing, 2022, 162: No.107954. |
| 17 | Kingetsu Y, Hamasuna Y. Jensen–Shannon divergence-based k-medoids clustering[J]. Journal of Advanced Computational Intelligence and Intelligent Informatics, 2021, 25(2): 226-233. |
| 18 | Yang L, Zhu Q, Huang J, et al. Adaptive edited natural neighbor algorithm[J]. Neurocomputing, 2017, 230: 427-433. |
| 19 | Dai Q Z, Xiong Z Y, Xie J, et al. A novel clustering algorithm based on the natural reverse nearest neighbor structure[J]. Information Systems, 2019, 84: 1-16. |
| 20 | Zhou S, Zhao Y, Guan J, et al. A neighborhood-based clustering algorithm[C]∥Pacific-Asia Conference on Knowledge Discovery and Data Mining,Tokyo, Japan, 2005: 361-371. |
| 21 | Huang J, Zhu Q, Yang L, et al. QCC: a novel clustering algorithm based on Quasi-Cluster centers[J]. Machine Learning, 2017, 106(3): 337-357. |
| 22 | Tenenbaum J B, de Silva V, Langford J C. A global geometric framework for nonlinear dimensionality reduction[J]. Science, 2000, 290(5500): 2319-2323. |
| 23 | Cheng D, Zhang S, Huang J. Dense members of local cores-based density peaks clustering algorithm[J]. Knowledge-Based Systems, 2020,193:No.105454. |
| 24 | Jiang B, Pei J, Tao Y, et al. Clustering uncertain data based on probability distribution similarity[J]. IEEE Transactions on Knowledge and Data Engineering, 2011, 25(4): 751-763. |
| 25 | Cai Y, Zhang Y, Qu J, et al. Differential privacy preserving dynamic data release scheme based on Jensen-Shannon divergence[J]. China Communications, 2022, 19(6): 11-21. |
| [1] | 张玺君,余光杰,崔勇,尚继洋. 基于聚类算法和图神经网络的短时交通流预测[J]. 吉林大学学报(工学版), 2024, 54(6): 1593-1600. |
| [2] | 刘迪,孙耀,胡云峰,陈虹. 基于密度聚类的商用车编队策略[J]. 吉林大学学报(工学版), 2024, 54(5): 1459-1468. |
| [3] | 吕莉,朱梅子,康平,韩龙哲. 二阶K近邻和多簇合并的密度峰值聚类算法[J]. 吉林大学学报(工学版), 2024, 54(5): 1417-1425. |
| [4] | 陈桂珍,程慧婷,朱才华,李昱燃,李岩. 考虑驾驶员生理信息的城市交叉口风险评估方法[J]. 吉林大学学报(工学版), 2024, 54(5): 1277-1284. |
| [5] | 张西广,张龙飞,马钰锡,樊银亭. 基于密度峰值的海量云数据模糊聚类算法设计[J]. 吉林大学学报(工学版), 2024, 54(5): 1401-1406. |
| [6] | 曲福恒,潘曰涛,杨勇,胡雅婷,宋剑飞,魏成宇. 基于加权空间划分的高效全局K-means聚类算法[J]. 吉林大学学报(工学版), 2024, 54(5): 1393-1400. |
| [7] | 宋世军,樊敏. 基于随机森林算法的大数据异常检测模型设计[J]. 吉林大学学报(工学版), 2023, 53(9): 2659-2665. |
| [8] | 张雅丽,付锐,袁伟,郭应时. 考虑能耗的进出站驾驶风格分类及识别模型[J]. 吉林大学学报(工学版), 2023, 53(7): 2029-2042. |
| [9] | 刘状壮,郑文清,郑健,李轶峥,季鹏宇,沙爱民. 基于网格化的路表温度感知技术[J]. 吉林大学学报(工学版), 2023, 53(6): 1746-1755. |
| [10] | 康耀龙,冯丽露,张景安,曹素娥. 基于谱聚类的不确定数据集中快速离群点挖掘算法[J]. 吉林大学学报(工学版), 2023, 53(4): 1181-1186. |
| [11] | 姚荣涵,徐文韬,郭伟伟. 基于因子长短期记忆的驾驶人接管行为及意图识别[J]. 吉林大学学报(工学版), 2023, 53(3): 758-771. |
| [12] | 郭柏苍,雒国凤,金立生,谢宪毅,孙栋先. 面向自动驾驶虚拟测试的变道切入场景库构建方法[J]. 吉林大学学报(工学版), 2023, 53(11): 3130-3140. |
| [13] | 翁剑成,魏瑞聪,何寒梅,徐海辉,王晶晶. 基于关联路链组的城市路网短时交通流预测模型[J]. 吉林大学学报(工学版), 2023, 53(11): 3104-3112. |
| [14] | 蒋林,杨立,张文俊,张琼玉,吴艳霞. 在障碍物检测时对斜坡点云的检测处理算法[J]. 吉林大学学报(工学版), 2023, 53(11): 3221-3228. |
| [15] | 曹倩,李志慧,陶鹏飞,马永建,杨晨曦. 考虑风险异质特性的路网交通事故风险评估方法[J]. 吉林大学学报(工学版), 2023, 53(10): 2817-2825. |
|
||