基于加权空间划分的高效全局K-means聚类算法

doi:10.13229/j.cnki.jdxbgxb.20221338

摘要/Abstract

摘要：

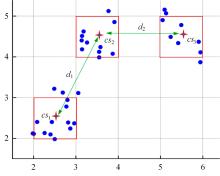
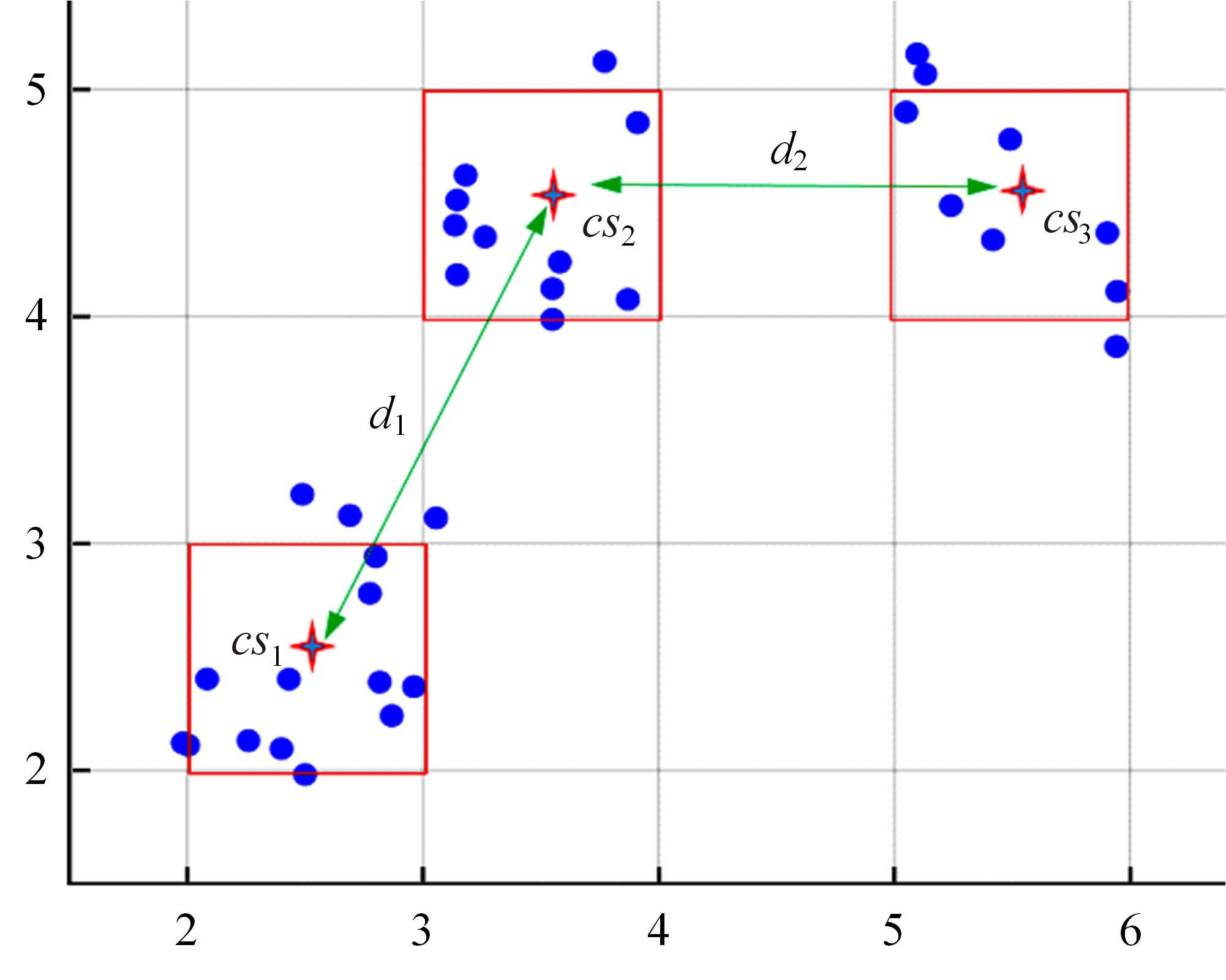
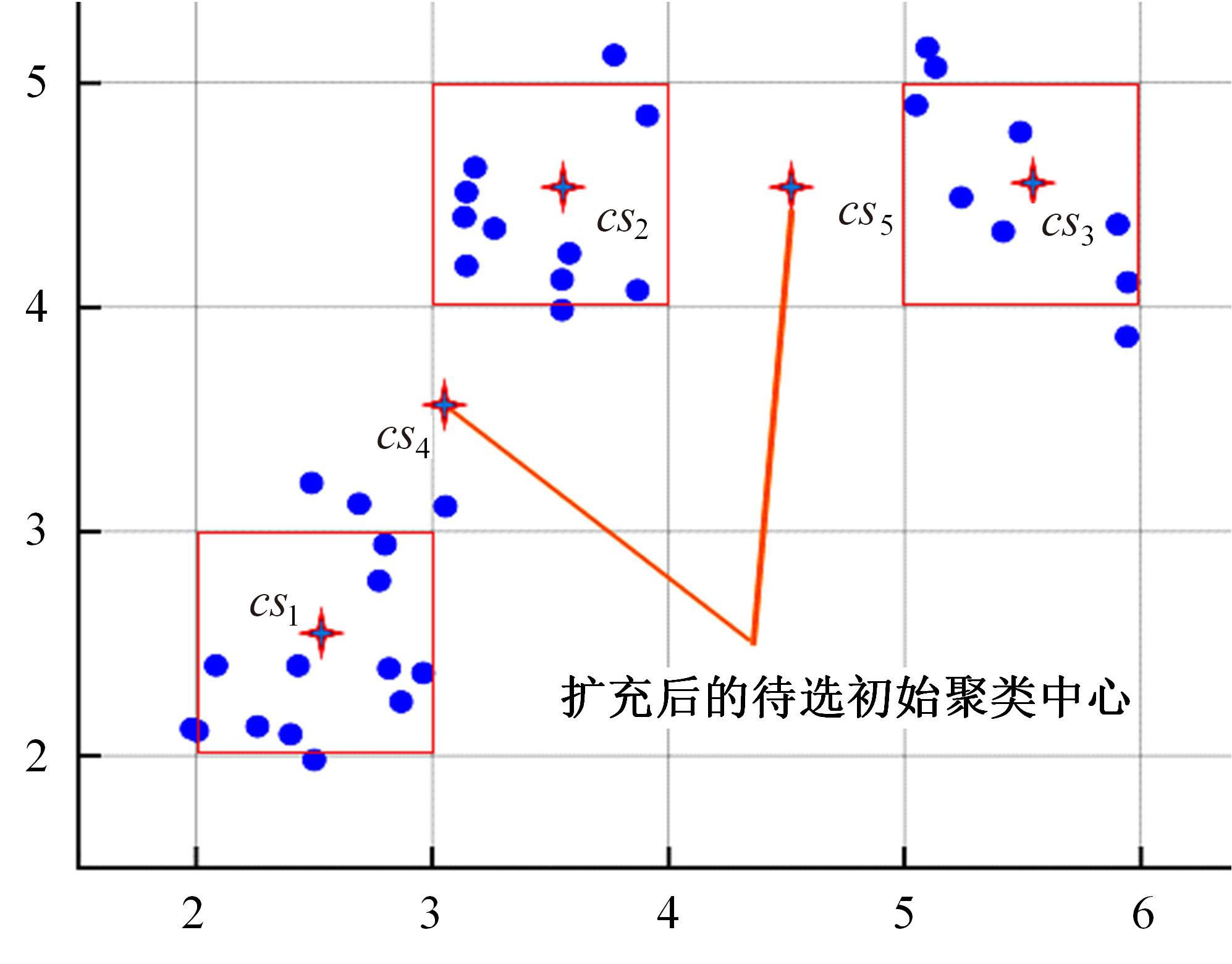
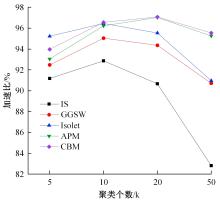
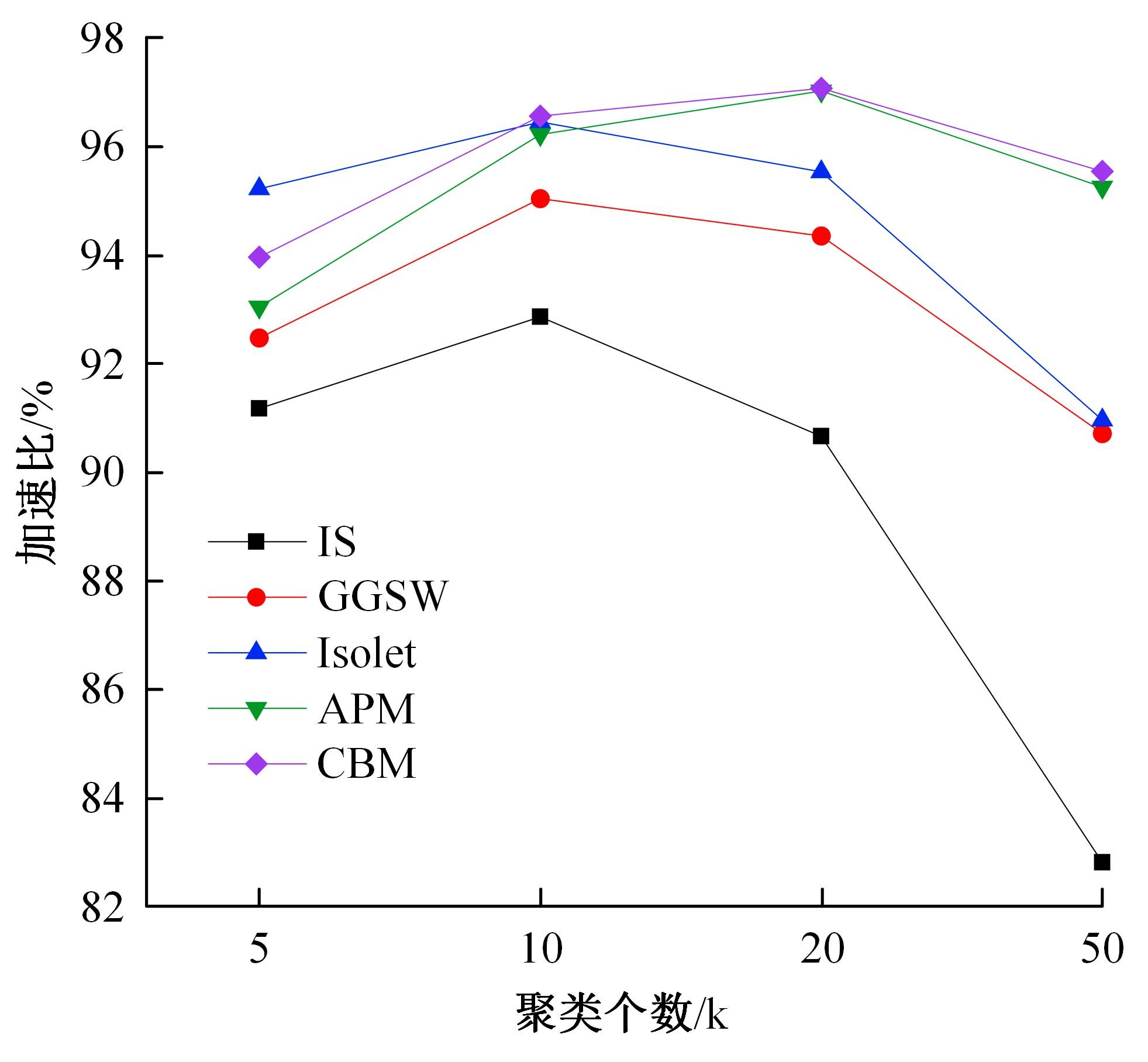
针对全局K-means聚类算法穷举样本点导致计算量大的问题，提出一种基于加权空间划分的高效全局K-means聚类算法。算法首先对样本空间进行网格划分，然后提出密度准则与距离准则对网格进行过滤，保留密度较大且相互距离较远的网格作为候选中心网格。为避免全局K-means算法只在样本集中选取候选中心的局限性，提出权重准则和中心迭代策略扩充候选中心，增加候选中心多样性。最后，通过增量聚类方式遍历候选中心得到最终的聚类结果。在UCI数据集上的实验结果表明：与全局K-means算法相比，新算法在保证聚类精度的前提下，计算效率平均提高了89.39%~95.79%。与K-means++、IK-+和近期提出的CD算法相比，新算法精度更高，并且克服了因随机初始化导致的聚类结果不稳定问题。

关键词: 人工智能, K-means算法, 聚类中心, 网格划分, 权重, 增量式聚类

Abstract:

Aiming at the problem of large amount of calculation caused by exhaustive sample points in global K-means clustering algorithm， this paper proposes an efficient global K-means clustering algorithm based on weighted space partition. Firstly， the sample space is divided into grids， and then the density criterion and distance criterion are proposed to filter the grids， and the grids with large density and far distance from each other are retained as candidate center grids. In order to avoid the limitation that the global K-means algorithm only selects candidate centers in the sample set， the weight criterion and the center iteration strategy are proposed to expand the candidate centers and increase the diversity of the candidate centers. Finally， the candidate centers were traversed by incremental clustering to obtain the final clustering result. The experimental results on UCI data sets show that compared with the global K-means algorithm， the computational efficiency of the new algorithm is improved by 89.39%~95.79% on average under the premise of ensuring the clustering accuracy. Compared with K-means ++， IK-+ and the recently proposed CD algorithm， the new algorithm has higher accuracy and overcomes the problem of unstable clustering results caused by random initialization.

Key words: artificial intelligence, K-means algorithm, clustering center, multidimensional grid space, weight, incremental clustering

中图分类号:

TP391

曲福恒,潘曰涛,杨勇,胡雅婷,宋剑飞,魏成宇. 基于加权空间划分的高效全局K-means聚类算法[J]. 吉林大学学报(工学版), 2024, 54(5): 1393-1400.

Fu-heng QU,Yue-tao PAN,Yong YANG,Ya-ting HU,Jian-fei SONG,Cheng-yu WEI. An efficient global K-means clustering algorithm based on weighted space partitioning[J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(5): 1393-1400.

图/表 8

图1

图2

图3

图4

表1

表2

表3

图5

参考文献 18

1	Rahman M A, Islam M Z. A hybrid clustering technique combining a novel genetic algorithm with K-means[J]. Knowledge-Based Systems, 2014, 71: 345-365.
2	Harjanti T W, Setiyani H, Trianto J, et al. Classification of mint leaf types based on the image using euclidean distance and K-means clustering with shape and texture feature extraction[J]. Tech-E, 2022, 5(2): 115-124.
3	刘仲民, 李战明, 李博皓,等. 基于稀疏矩阵的谱聚类图像分割算法[J]. 吉林大学学报: 工学版, 2017,47(4): 1308-1313.
	Liu Zhong-min, Li Zhan-ming, Li Bo-hao, et al. Spectral clustering image segmentation based on sparse matrix[J]. Journal of Jilin University (Engineering and Technology Edition), 2017, 47(4): 1308-1313.
4	Lim Z Y, Ong L Y, Leow M C. A review on clustering techniques: creating better user experience for online roadshow[J]. Future Internet, 2021, 13(9): 233.
5	张萌谡, 刘春天, 李希今, 等. 基于K-means聚类算法的绩效考核模糊综合评价系统设计[J]. 吉林大学学报: 工学版, 2021, 51(5): 1851-1856.
	Zhang Meng-su, Liu Chun-tian, Li Xi-jin, et al. Design of fuzzy comprehensive evaluation system for performance appraisal based on K-means clustering algorithm[J]. Journal of Jilin University (Engineering and Technology Edition), 2021, 51(5): 1851-1856.
6	Fränti P, Sieranoja S. How much can K-means be impr-oved by using better initialization and repeats?[J]. Pattern Recognition, 2019, 93: 95-112.
7	杨勇, 陈强, 曲福恒, 等. 基于模拟划分的SP-K-means-+算法[J]. 吉林大学学报: 工学版, 2021, 51(5): 1808-1816.
	Yang Yong, Chen Qiang, Qu Fu-heng, et al. SP-K-means-+ algorithm based on simulated partition[J]. Journal of Jilin University (Engineering and Technology Edition), 2021, 51(5): 1808-1816.
8	Geng X, Mu Y, Mao S, et al. An improved K-means algorithm based on fuzzy metrics[J]. IEEE Access, 2020, 8: 217416-217424.
9	邵伦, 周新志, 赵成萍, 等. 基于多维网格空间的改进 K-means 聚类算法[J]. 计算机应用,2018, 38(10): 2850-2855.
	Shao Lun, Zhou Xin-zhi, Zhao Cheng-ping, et al. Improved K-means clustering algorithm based on multidimensional grid space[J]. Computer Application, 2018,38(10): 2850-2855.
10	Manochandar S, Punniyamoorthy M, Jeyachitra R K. Development of new seed with modified validity measures for K-means clustering[J]. Computers & Industrial Engineering, 2020, 141: 106290.
11	Zhang S, Liu Z, Chen X, et al. Parallel implementation of improved K-means based on a cloud platform[J]. Information Technology and Control, 2019, 48(4): 673-681.
12	Arthur D, Vassilvitskii S. K-means++ the advantages of careful seeding[C]∥Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete algorithms, New Orleans, USA, 2007: 1027-1035.
13	Lattanzi S, Sohler C. A better K-means++ algorithm via local search[C]∥Proceedings of the 36th International Conference on Machine Learning,Long Beach,USA,2019: 3662-3671.
14	Choo D, Grunau C, Portmann J, et al. K-means++: few more steps yield constant approximation[C]∥Proceedings of the 37th International Conference on Machine Learning, Vienna, Austria, 2020: 1909-1917.
15	Ismkhan H. Ik-means-+: an iterative clustering algorithm based on an enhanced version of the K-means[J]. Pattern Recognition, 2018, 79: 402-413.
16	Chowdhury K, Chaudhuri D, Pal A K. An entropy-based initialization method of K-means clustering on the optimal number of clusters[J]. Neural Computing and Applications, 2021, 33: 6965-6982.
17	Nie F, Xue J, Wu D, et al. Coordinate descent meth-od for k-means[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021,44(5): 2371-2385.
18	Likas A, Vlassis N, Verbeek J J. The global k-means clustering algorithm[J]. Pattern Recognition, 2003,36(2): 451-461.

相关文章 15

[1]	孙帅帅,冯春晓,张良. 基于离散采样的多模态四足机器人路径规划[J]. 吉林大学学报(工学版), 2024, 54(4): 1120-1128.
[2]	金志刚,苏仁鋆,赵晓芳. 基于异质图网络的心理评估方法[J]. 吉林大学学报(工学版), 2024, 54(4): 1078-1085.
[3]	高敬鹏,王国轩,高路. 基于异步合作更新的LSTM-MADDPG多智能体协同决策算法[J]. 吉林大学学报(工学版), 2024, 54(3): 797-806.
[4]	刘浏,丁鲲,刘姗姗,刘茗. 基于机器阅读理解的事件检测方法[J]. 吉林大学学报(工学版), 2024, 54(2): 533-539.
[5]	傅丽芳,陈卓,敖长林. 基于分类和回归树决策树的网络大数据集离群点动态检测算法[J]. 吉林大学学报(工学版), 2023, 53(9): 2620-2625.
[6]	宋世军,樊敏. 基于随机森林算法的大数据异常检测模型设计[J]. 吉林大学学报(工学版), 2023, 53(9): 2659-2665.
[7]	李健,熊琦,胡雅婷,刘孔宇. 基于Transformer和隐马尔科夫模型的中文命名实体识别方法[J]. 吉林大学学报(工学版), 2023, 53(5): 1427-1434.
[8]	谢波,高榕,许富强,田彦涛. 低附着路况条件下人车共享转向系统稳定控制[J]. 吉林大学学报(工学版), 2023, 53(3): 713-725.
[9]	马月坤,郝益锋. 考虑特征稀疏特性的短文本命名实体快速识别方法[J]. 吉林大学学报(工学版), 2023, 53(12): 3529-3535.
[10]	刘春晖,王思长,郑策,陈秀连,郝春蕾. 基于深度学习的室内导航机器人避障规划算法[J]. 吉林大学学报(工学版), 2023, 53(12): 3558-3564.
[11]	白丽丽,姜封国,周玉明,曾枭. 基于改进鲸鱼算法的结构可靠性优化设计[J]. 吉林大学学报(工学版), 2023, 53(11): 3160-3165.
[12]	白天,徐明蔚,刘思铭,张佶安,王喆. 基于深度神经网络的诉辩文本争议焦点识别[J]. 吉林大学学报(工学版), 2022, 52(8): 1872-1880.
[13]	王生生,姜林延,杨永波. 基于最优传输特征选择的医学图像分割迁移学习[J]. 吉林大学学报(工学版), 2022, 52(7): 1626-1638.
[14]	田皓宇,马昕,李贻斌. 基于骨架信息的异常步态识别方法[J]. 吉林大学学报(工学版), 2022, 52(4): 725-737.
[15]	方世敏. 基于频繁模式树的多来源数据选择性集成算法[J]. 吉林大学学报(工学版), 2022, 52(4): 885-890.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

数据集	数据个数	特征维数
Image Segmentation（IS）	2 310	19
Gender Gap in Spanish WP（GGSW）	4 746	19
Isolet	7 797	617
AI4I 2020 Predictive Maintenance（APM）	10 000	11
Condition Based Maintenance（CBM）	11 934	16

数据集	聚类个数	SSE
数据集	聚类个数	KM	K-means++	CD	IK-+	GKM	本文
IS	K=5	2.006 0E+07	2.059 8E+07	2.028 3E+07	1.962 8E+07	1.714 3E+07	1.714 3E+07
	K=10	1.137 1E+07	1.221 4E+07	1.135 0E+07	1.209 8E+07	9.967 2E+06	1.012 8E+07
	K=20	6.664 2E+06	6.165 8E+06	6.456 7E+06	5.481 0E+06	5.132 8E+06	5.299 9E+06
	K=50	3.525 9E+06	2.538 2E+06	3.399 1E+06	2.344 2E+06	2.278 6E+06	2.267 0E+06
GGSW	K=5	1.098 6E+24	1.064 8E+24	1.097 3E+24	1.060 9E+24	1.019 5E+24	1.019 5E+24
	K=10	5.237 9E+23	5.103 3E+23	5.225 7E+23	5.001 5E+23	4.691 1E+23	4.696 6E+23
	K=20	2.524 1E+23	2.242 6E+23	2.513 3E+23	2.267 7E+23	2.072 1E+23	2.095 8E+23
	K=50	7.839 6E+22	5.009 4E+22	7.783 6E+22	6.487 3E+22	4.556 1E+22	4.411 7E+22
Isolet	K=5	6.170 0E+05	6.175 0E+05	6.163 8E+05	6.168 8E+05	6.286 5E+05	6.136 5E+05
	K=10	5.360 6E+05	5.376 6E+05	5.346 9E+05	5.401 5E+05	5.435 6E+05	5.306 8E+05
	K=20	4.671 5E+05	4.653 6E+05	4.681 8E+05	4.664 0E+05	4.606 2E+05	4.663 0E+05
	K=50	4.055 0E+05	4.048 5E+05	4.049 2E+05	4.021 2E+05	4.070 3E+05	4.038 9E+05
APM	K=5	7.270 2E+07	7.100 2E+07	7.267 4E+07	7.185 1E+07	7.118 3E+07	7.118 3E+07
	K=10	3.231 8E+07	3.230 8E+07	3.231 8E+07	3.233 7E+07	3.228 6E+07	3.226 6E+07
	K=20	1.611 7E+07	1.654 3E+07	1.610 8E+07	1.600 1E+07	1.580 0E+07	1.593 6E+07
	K=50	6.902 6E+06	6.736 6E+06	6.846 1E+06	6.461 5E+06	6.297 1E+06	6.306 4E+06
CBM	K=5	3.173 0E+11	1.491 5E+11	3.185 3E+11	1.542 5E+11	1.149 0E+11	1.670 0E+11
	K=10	7.165 0E+10	1.191 0E+09	7.165 0E+10	1.300 3E+09	1.191 0E+09	1.191 0E+09
	K=20	2.147 8E+10	8.484 7E+07	2.147 4E+10	8.657 5E+07	8.176 0E+07	8.159 0E+07
	K=50	1.427 0E+08	2.389 2E+07	1.426 6E+08	2.275 9E+07	2.182 9E+07	2.624 3E+07

聚类个数	K-means++	CD	IK-+	GKM	本文
K=5	11.13%	-0.25%	11.63%	17.15%	14.35%
K=10	18.65%	0.13%	19.10%	23.96%	24.15%
K=20	23.20%	0.68%	25.68%	28.77%	27.67%
K=50	29.99%	1.06%	28.41%	34.07%	34.01%
平均值	20.74%	0.41%	21.20%	25.99%	25.05%