基于随机充电需求的充电桩优化双层模型

doi:10.13229/j.cnki.jdxbgxb.20221364

吉林大学学报(工学版) ›› 2024, Vol. 54 ›› Issue (8): 2238-2244.doi: 10.13229/j.cnki.jdxbgxb.20221364

• 交通运输工程·土木工程 • 上一篇下一篇

基于随机充电需求的充电桩优化双层模型

闫云娟¹(),查伟雄²(),石俊刚²,严丽平³

^1.华东交通大学机电与车辆工程学院，江西南昌 330013
^2.华东交通大学交通运输与物流学院，江西南昌 330013
^3.华东交通大学软件学院，江西南昌 330013

收稿日期:2022-10-25 出版日期:2024-08-01 发布日期:2024-08-30
通讯作者: 查伟雄 E-mail:xiaoyan921@sohu.com;jxzhawx@sina.com
作者简介:闫云娟（1977-），女，讲师，博士研究生. 研究方向：交通系统规划.E-mail：xiaoyan921@sohu.com
基金资助:
国家自然科学基金项目(72361012);江西省自然科学基金面上项目(20224BAB204014);江西省领军人才项目(S2021GDKX1442)

Double layer optimization model of charging pile based on random charging demand

Yun-juan YAN¹(),Wei-xiong ZHA²(),Jun-gang SHI²,Li-ping YAN³

^1.College of Mechatronics & Vehicle Engineering，East China Jiaotong University，Nanchang 330013，China
^2.Institute of Transportation and Economics，East China Jiaotong University，Nanchang 330013，China
^3.School of Software，East China Jiaotong University，Nanchang 330013，China

Received:2022-10-25 Online:2024-08-01 Published:2024-08-30
Contact: Wei-xiong ZHA E-mail:xiaoyan921@sohu.com;jxzhawx@sina.com

摘要/Abstract

摘要：

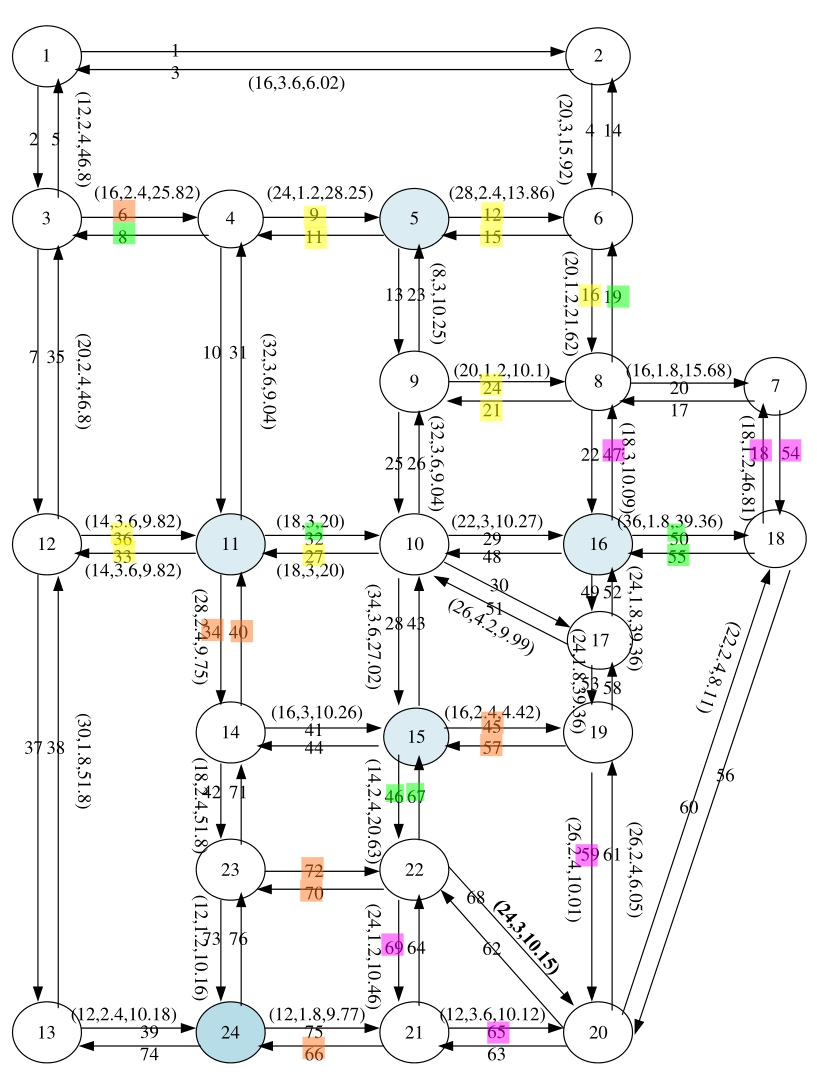
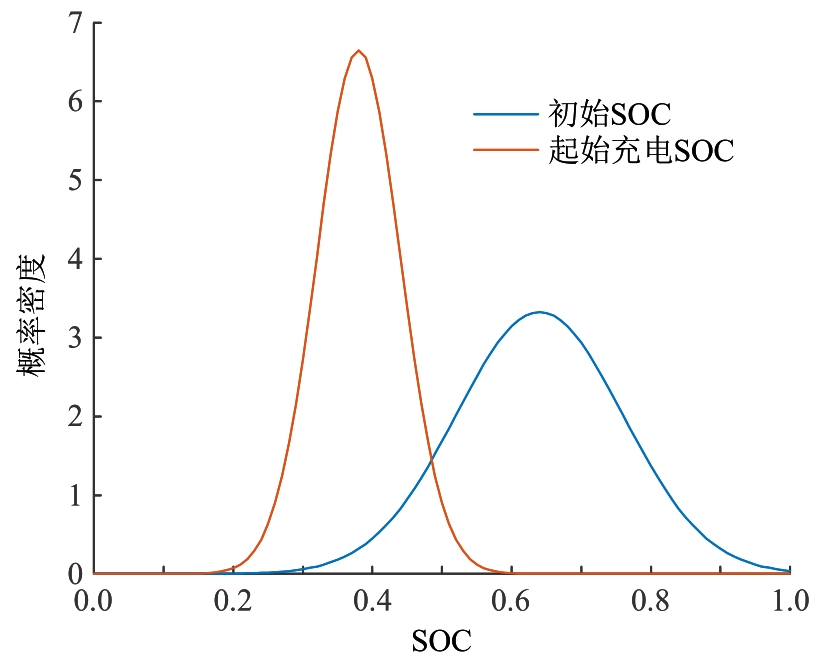
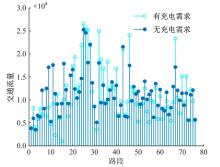
在具有随机充电需求的混合交通网络里，为确定合理的充电桩配置数，构建了双层规划模型。上层模型以建设成本净现值、顾客流失成本、超出忍耐时间成本之和最小为目标；下层模型以用户广义出行成本最小为目标，描述路网流量分配与充电设施部署位置的相互作用。模型利用差分进化算法与Frank-Wolfe算法相嵌套进行网络均衡配流及充电桩配置寻优仿真。结果表明：模型能有效模拟和预测网络均衡交通流、随机充电流、排队损失率和充电桩最优配置数。

关键词: 交通运输规划与管理, 双层规划模型, Frank-Wolfe算法, 差分进化算法, 充电桩配置

Abstract:

In the mixed transportation network with random charging demand， a bi-level programming model is built to determine the reasonable number of charging piles. The upper model aims to minimize the sum of the net present value of the construction cost， the cost of customer loss， and the cost of exceeding the endurance time； the lower level model aims to minimize the user's generalized travel cost to describe the interaction between the road network flow allocation and the location of charging facilities. The model uses differential evolution algorithm and Frank-Wolfe algorithm nested to carry out traffic equilibrium assignment and charging pile configuration optimization simulation. The results show that the model can effectively simulate and predict network equilibrium traffic flow， random charging flow， queuing loss rate and optimal number of charging piles.

Key words: transportation planning and management, bi-level programming model, Frank-Wolfe algorithm, differential evolution algorithm, charging pile configuration

中图分类号:

U491

闫云娟,查伟雄,石俊刚,严丽平. 基于随机充电需求的充电桩优化双层模型[J]. 吉林大学学报(工学版), 2024, 54(8): 2238-2244.

Yun-juan YAN,Wei-xiong ZHA,Jun-gang SHI,Li-ping YAN. Double layer optimization model of charging pile based on random charging demand[J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(8): 2238-2244.

图/表 5

图1

表1

建模参数"

参数	值	参数	值	参数	值
$C u, f i$	6.2万元	$C g$	2.67元/km	$μ 1$	0.64
$C s$	2.76万元/桩	$C e$	0.216元/km	$μ 2$	0.35
$C T l o s t$	50元/h	$w m a x$	30 min	$α 1$	0.5
$C B l o s t$	0.25元/（辆?h）	$C u, o h e r i$	640元/（年?车位）	$α 2$	0.3
$β g$	0.6min/元	$β e$	0.6 min/元	$σ 1$	0.12
$l$	10年	$ω a v e r a g e$	0.36度/h	$σ 2$	0.08
$i r$	0.1	$H$	1000	$ρ m i n$	0.6
$N s$	200	$C R$	0.01	$F$	0.4
$S u$	100	h	0.0001	$M s$	50

表1

图2

表2

图3

参考文献 16

1	国务院办公厅.国务院办公厅印发《新能源汽车产业发展规划(2021—2035年)》[R]. 北京:新华社, 2020.
2	Zhang H C, Moura S J, Hu Z C, et al. PEV fast-charging station siting and sizing on coupled transportation and power networks[J]. IEEE Trans. Smart Grid, 2018, 9(4): 2595-2605.
3	Islam M M, Shareef H, Mohamed A, et al. Optimal location and sizing of fast charging stations for electric vehicles by incorporating traffic and power networks[J]. IET Intelligent Transport Systems, 2018, 12(8): 947-957.
4	Xiang Y, Liu J, Li R, et al. Economic planning of electric vehicle charging stations considering traffic constraints and load profile templates[J]. Applied Energy, 2016, 178: 647-659.
5	Zhang Q, Zhu Y, Wang Z, et al. Siting and sizing of electric vehicle fast charging station based on quasi-dynamic traffic flow[J]. IET Renewable Power Generation, 2021, 14(2): 4204-4215.
6	罗清玉,田万利,贾洪飞. 考虑通勤需求的电动汽车充电站选址与定容模型[J]. 吉林大学学报: 工学版, 2019, 49(5): 1471-1477.
	Luo Qing-yu, Tian Wan-li, Jia Hong-fei. Location and capacity model of electric vehicle charging station
	considering commuting demand[J]. Journal of Jilin University (Engineering and Technology Edition), 2019, 49(5): 1471-1477.
7	Oda T, Aziz M, Mitani T, et al. Mitigation of congestion related to quick charging of electric vehicles based on waiting time and cost–benefit analyses: a Japanese case study[J]. Sustainable Cities and Society, 2018, 36: 99-106.
8	Bouguerra S, Layeb S B. Determining optimal deployment of electric vehicles charging stations: case of Tunis City, Tunisia[J]. Case Studies Transport Policy, 2019, 7(3): 628-642.
9	Jung J, Chow J Y J, Jayakrishnan R, et al. Stochastic dynamic itinerary interception refueling location problem with queue delay for electric taxi charging stations[J]. Transportation Research Part C: Emerging Technologies, 2014, 40: 123-142.
10	Payam S B, Abbas R G, Hosein K. Optimal fast charging station placing and sizing[J]. Applied Energy, 2014, 125: 289-299.
11	Khaksari A, Tsaousoglou G, Makris P, et al. Sizing of electric vehicle charging stations with smart charging capabilities and quality of service requirements[J]. Sustainable Cities and Society, 2021, 70(102872): 1-8.
12	梁辉, 杨超, 于绍政, 等. 电动汽车充电站选址和充电桩配置仿真优化[J] 计算机仿真, 2017, 34(8): 169-172.
	Liang Hui, Yang Chao, Yu Shao-zheng, et al. Research on electric vehicle siting of charging stations and configuration of charging pile based on simulation optimization method[J]. Computer Simulation, 2017, 34(8): 169-172.
13	SHEVDC上海市新能源汽车产业大数据研究报告2018上海市新能源汽车公共数据网[R]. https:∥www.shevdc.org/report/original_report/1898.jhtml.
14	闫云娟,查伟雄,石俊刚,等. 具有随机充电需求的混合动态网络平衡模型[J]. 吉林大学学报: 工学版, 2022, 52(1): 136-143.
	Yan Yun-juan, Zha Wei-xiong, Shi Jun-gang, et al. Mixed network equilibrium model with stochastic charging demand[J]. Journal of Jilin University (Engineering and Technology Edition), 2022, 52(1): 136-143.
15	He F, Yin Y, Lawphongpanich S. Network equilibrium models with battery electric vehicles[J]. Transp. Res. Part B, 2014, 67: 306-319.
16	Bar-Gear H. Transportation network test problems[R]. 2013. http:∥www.bgu.ac.il/bargera/tntp/

相关文章 15

[1]	曲大义,刘浩敏,杨子奕,戴守晨. 基于车路协同的交通瓶颈路段车流动态分配机制及模型[J]. 吉林大学学报(工学版), 2024, 54(8): 2187-2196.
[2]	阎奇武,邹忠亮. 减震结构阻尼器优化布置混合算法[J]. 吉林大学学报(工学版), 2024, 54(8): 2267-2274.
[3]	温晓岳,钱国敏,孔桦桦,缪月洁,王殿海. TrafficPro：一种针对城市信控路网的路段速度预测框架[J]. 吉林大学学报(工学版), 2024, 54(8): 2214-2222.
[4]	陈桂珍,程慧婷,朱才华,李昱燃,李岩. 考虑驾驶员生理信息的城市交叉口风险评估方法[J]. 吉林大学学报(工学版), 2024, 54(5): 1277-1284.
[5]	赵晓华,刘畅,亓航,欧居尚,姚莹,郭淼,杨海益. 高速公路交通事故影响因素及异质性分析[J]. 吉林大学学报(工学版), 2024, 54(4): 987-995.
[6]	杨秀建,贾晓寒,张生斌. 考虑汽车队列动态特性的混合交通流特性[J]. 吉林大学学报(工学版), 2024, 54(4): 947-958.
[7]	吴文静,熊康贝,贾洪飞,罗清玉. 城市群轨道交通直通线路优化设置方法[J]. 吉林大学学报(工学版), 2024, 54(3): 711-718.
[8]	范博松,邵春福. 城市轨道交通突发事件风险等级判别方法[J]. 吉林大学学报(工学版), 2024, 54(2): 427-435.
[9]	郑长江,胡欢,杜牧青. 考虑枢纽失效的多式联运快递网络结构设计[J]. 吉林大学学报(工学版), 2023, 53(8): 2304-2311.
[10]	王殿海,胡佑薇,蔡正义,曾佳棋,姚文彬. 基于BPR函数的城市道路间断流动态路阻模型[J]. 吉林大学学报(工学版), 2023, 53(7): 1951-1961.
[11]	李艳波,柳柏松,姚博彬,陈俊硕,渠开发,武奇生,曹洁宁. 考虑路网随机特性的高速公路换电站选址[J]. 吉林大学学报(工学版), 2023, 53(5): 1364-1371.
[12]	胡莹,邵春福,王书灵,蒋熙,孙海瑞. 基于共享单车骑行轨迹的骑行质量识别方法[J]. 吉林大学学报(工学版), 2023, 53(4): 1040-1046.
[13]	王占中,蒋婷,张景海. 基于模糊双边界网络模型的道路运输效率评价[J]. 吉林大学学报(工学版), 2023, 53(2): 385-395.
[14]	杨敏,张聪伟,李大韦,马晨翔. 基于贝叶斯网的空铁联程乘客出行满意度模型[J]. 吉林大学学报(工学版), 2023, 53(10): 2839-2846.
[15]	秦严严,杨晓庆,王昊. 智能网联混合交通流CO₂排放影响及改善方法[J]. 吉林大学学报(工学版), 2023, 53(1): 150-158.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

配置参数	最优结果
备选充电站位置	5	11	15	16	24
最优充电桩配置数/个	63	88	100	100	68
系统容量/个	95	132	150	150	102
均衡充电流量/（辆?h^-1）	474	584	685	1014	520
平均逗留时间/h	0.136	0.126	0.126	0.183	0.139
平均队长/（辆?h^-1）	65	74	86	146	77
损失率	0.005	2.68e-06	5.71e-06	0.21	0.007

基于随机充电需求的充电桩优化双层模型

Double layer optimization model of charging pile based on random charging demand

RICH HTML

PDF (PC)

摘要/Abstract

引用本文

使用本文

图/表 5

参考文献 16

相关文章 15

Metrics

本文评价

推荐阅读 10