加筋板结构可靠性拓扑优化与工程化设计

doi:10.13229/j.cnki.jdxbgxb.20221612

摘要/Abstract

摘要：

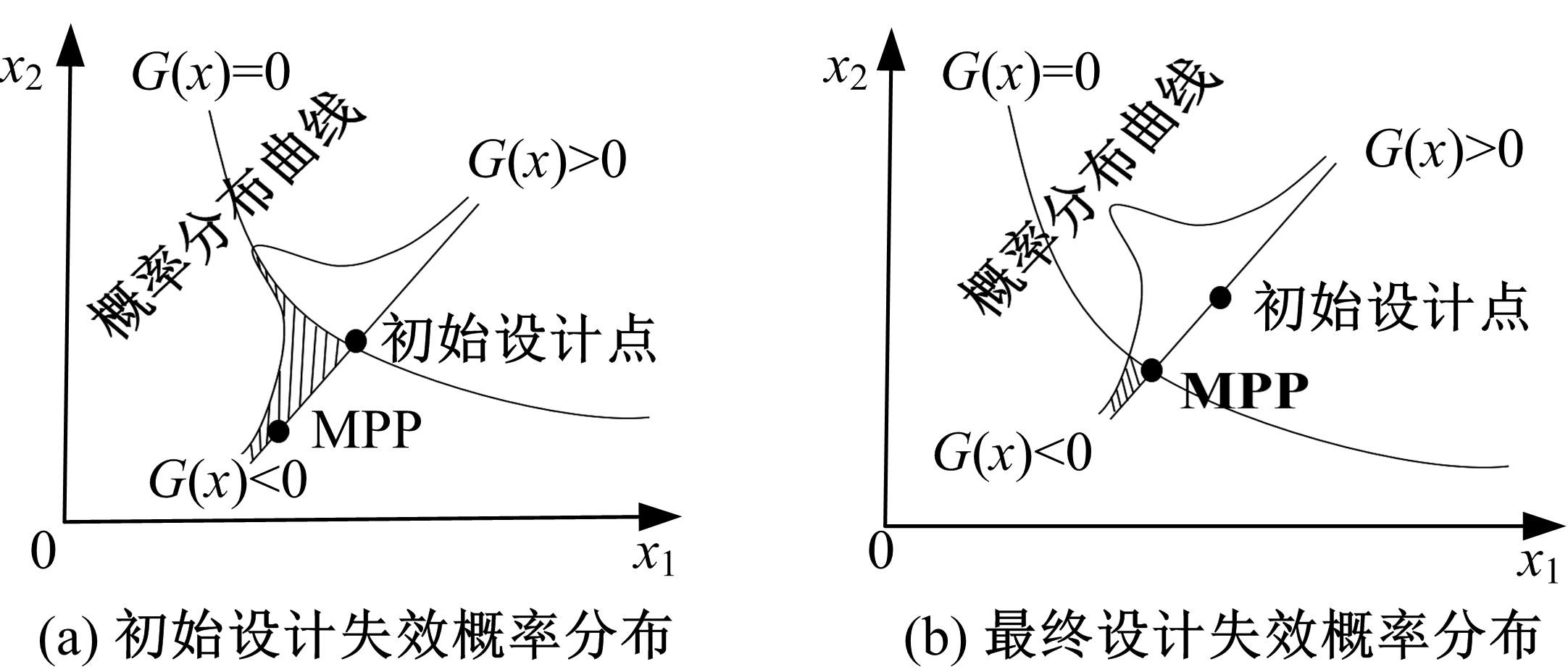
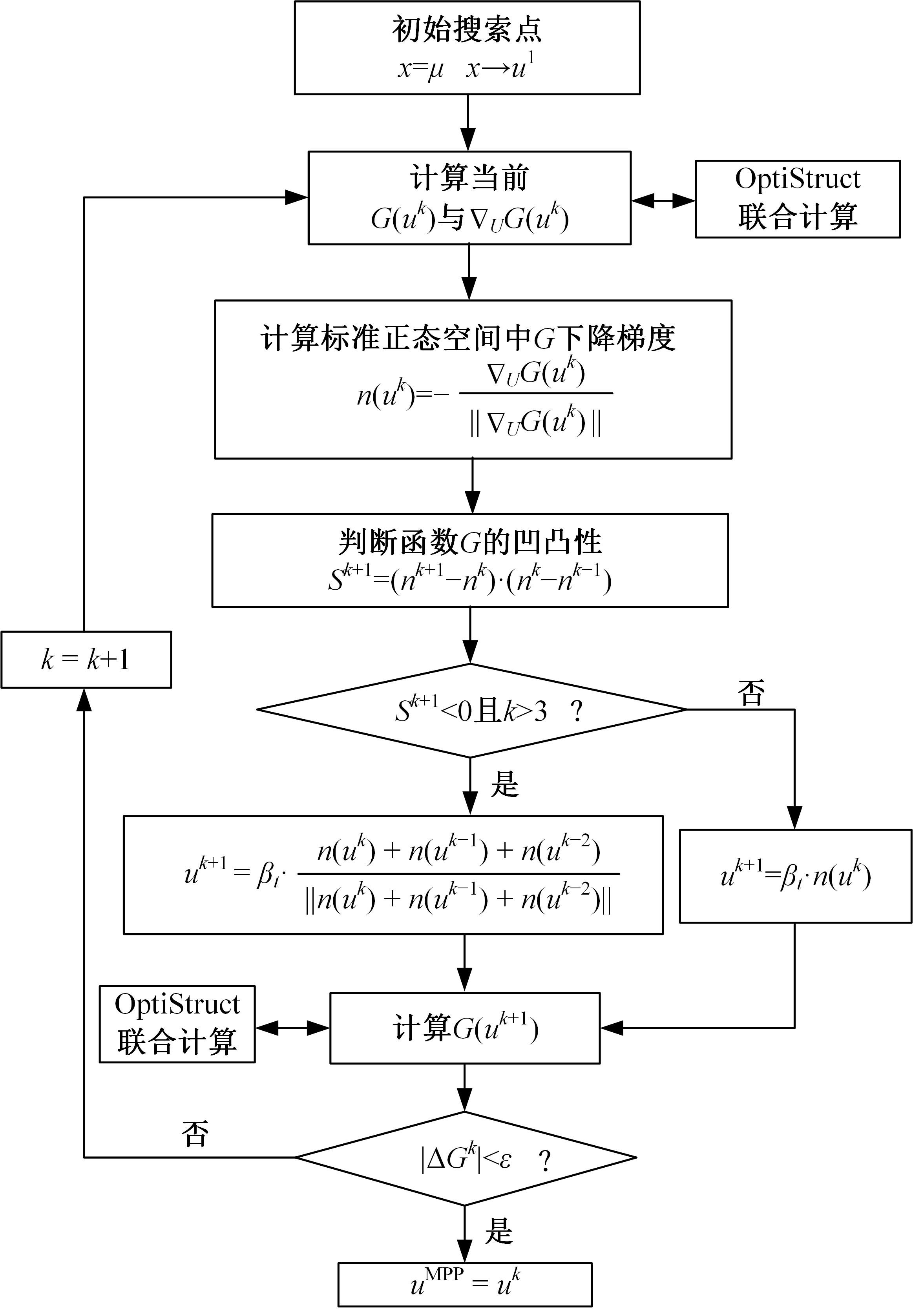
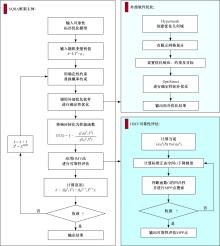
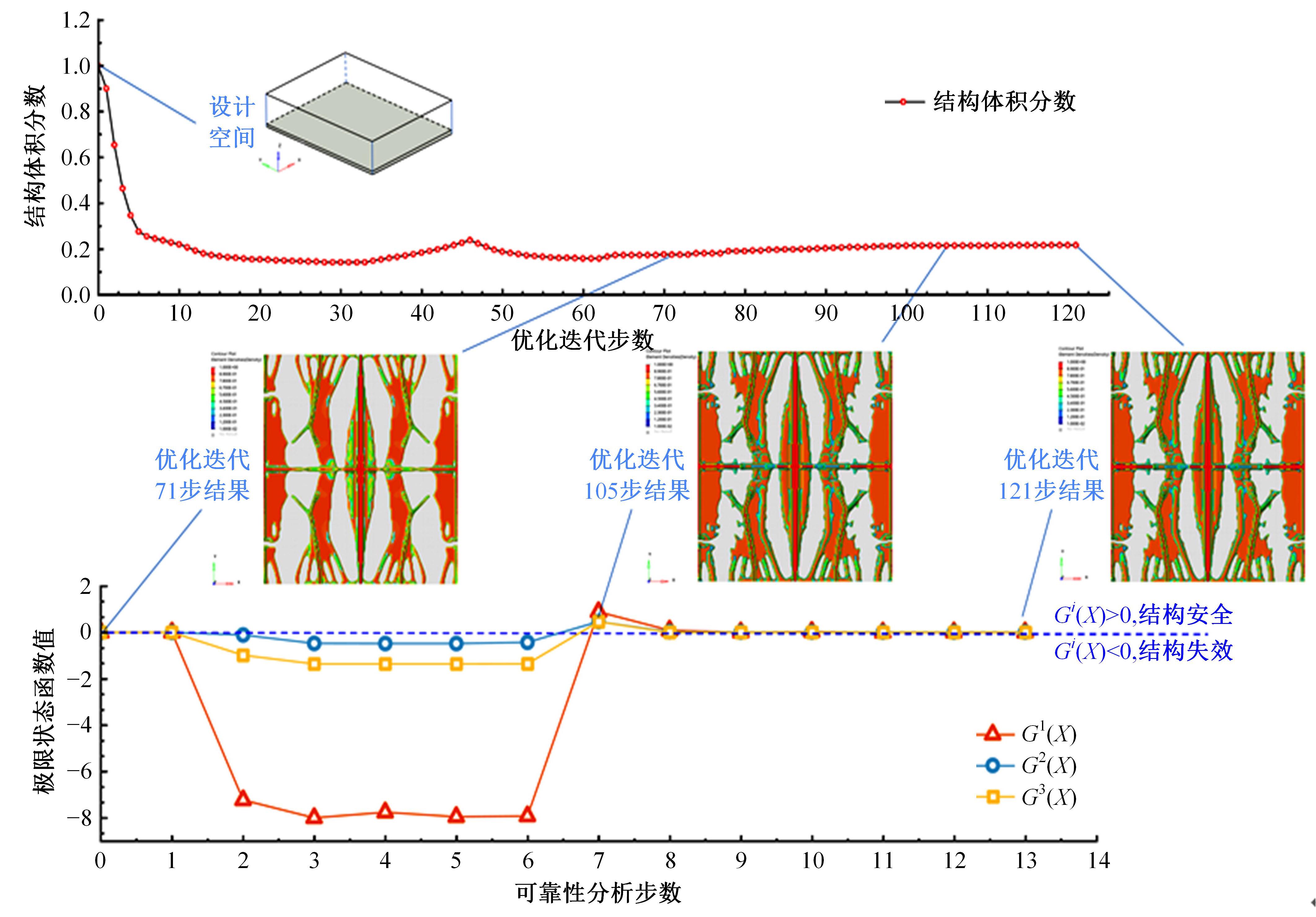
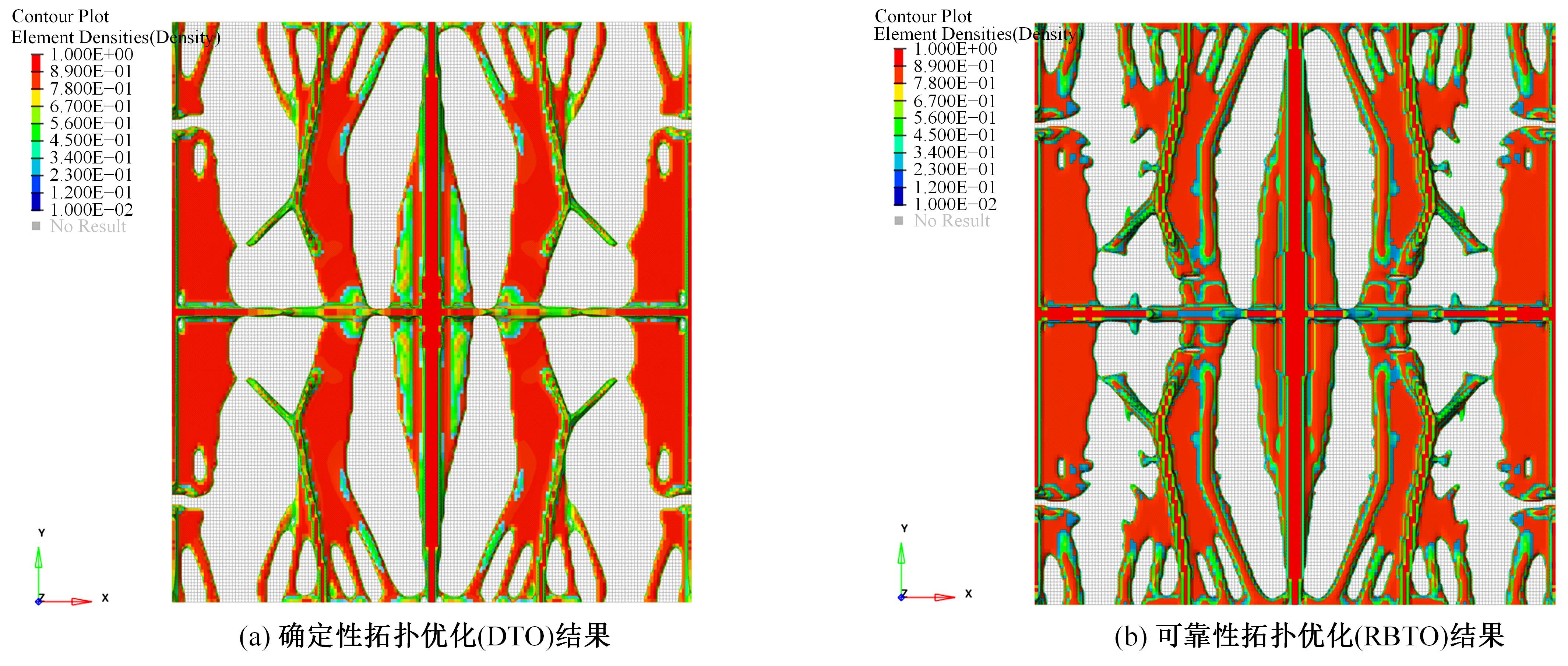
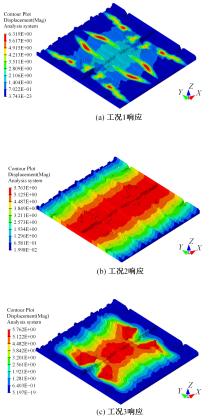
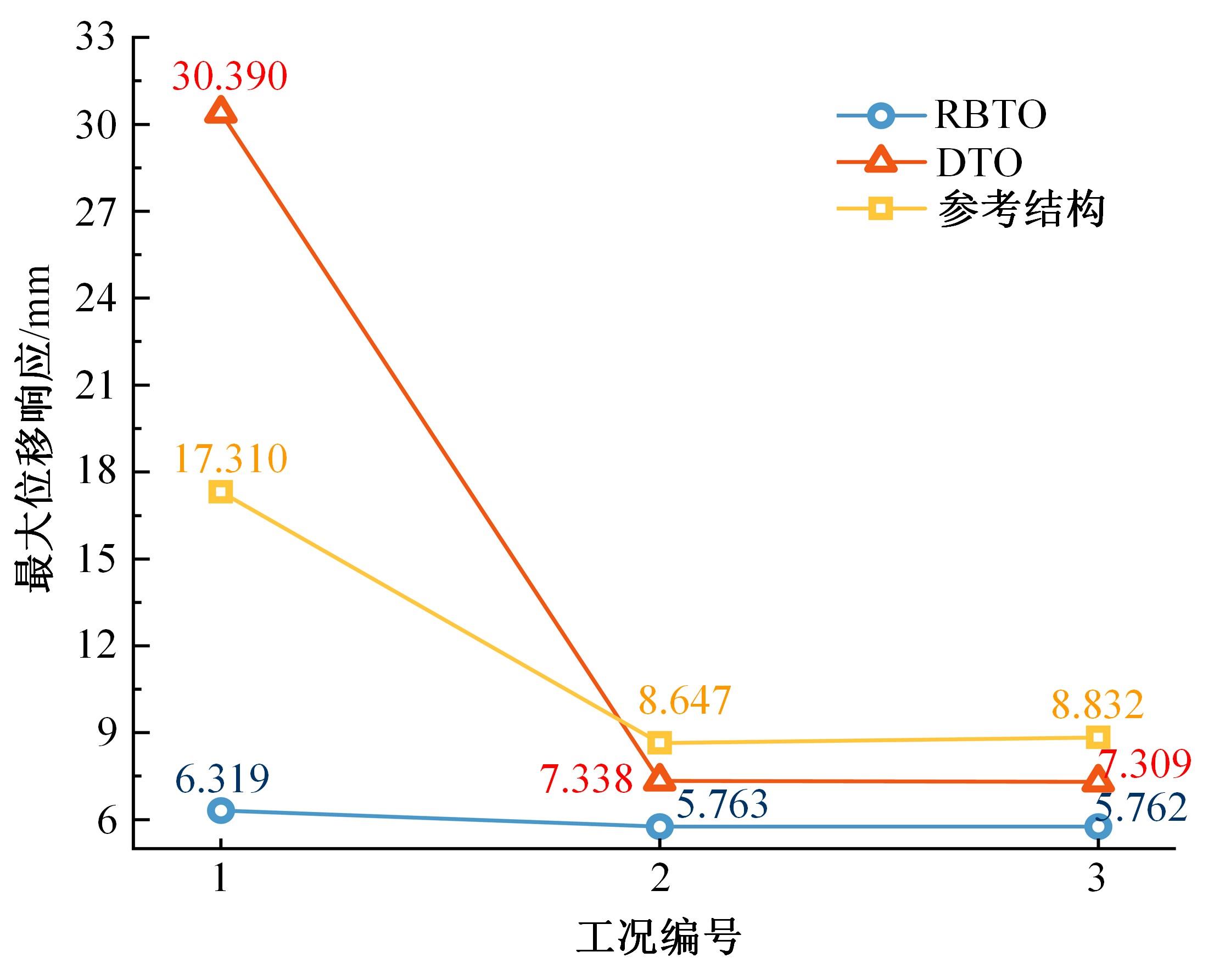
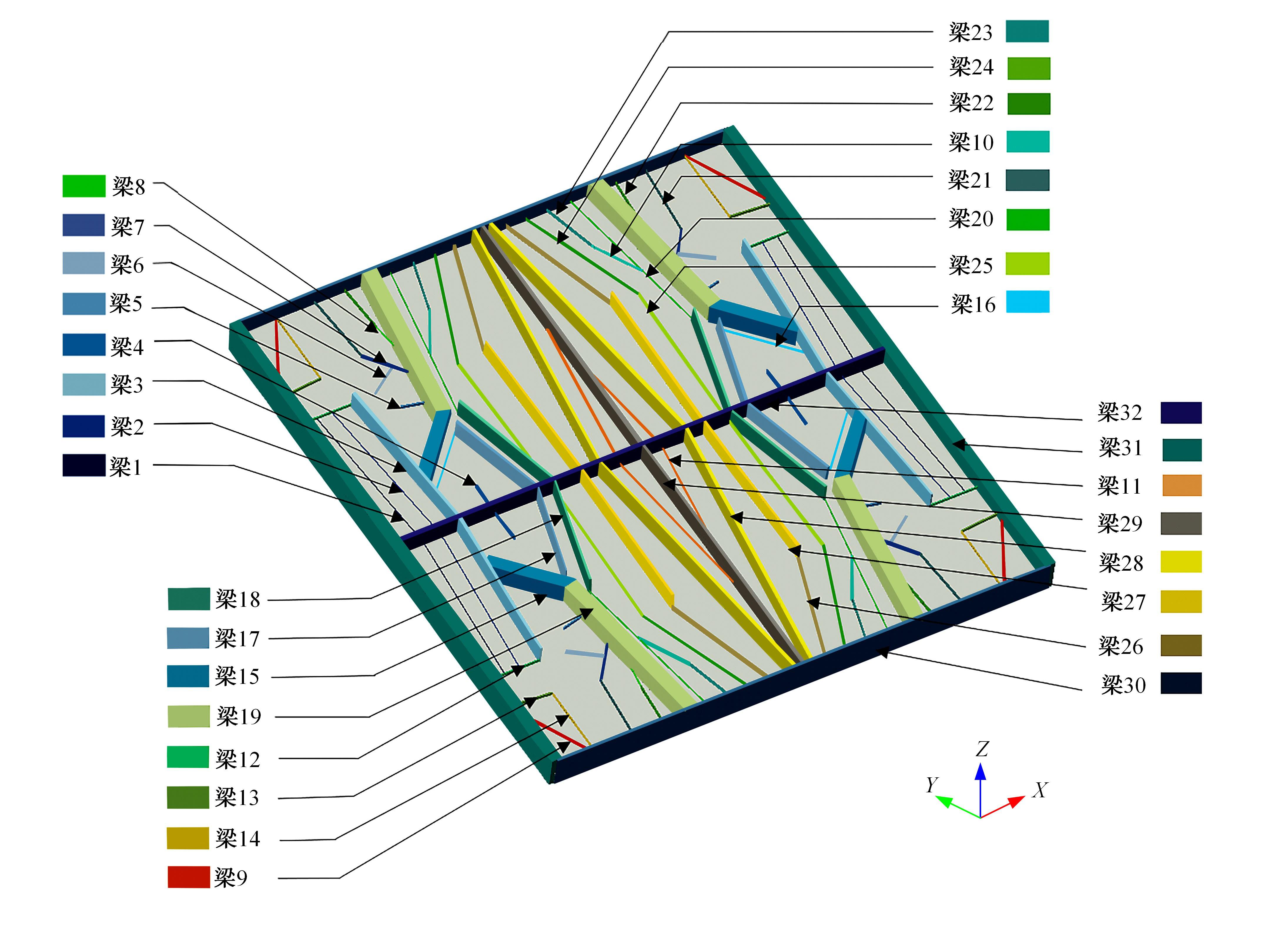
针对三维加筋板结构，为在保证其安全及可靠性的前提下实现轻量化与工程化设计，提出一种非嵌套的可靠性拓扑优化方法，并开展可靠性概念-详细组合优化设计。该方法借助序列优化及可靠性评估算法的解耦特性，应用变密度法内核下的外部优化软件进行确定性拓扑优化以提升优化效率；考虑载荷及材料随机性，将混合均值法应用于可靠性评估阶段的最可能失效点搜寻。进一步地，对可靠性概念设计进行布局解释并开展尺寸优化设计以实现工程化应用。研究表明：相较于确定性的拓扑优化方法，本文提出的可靠性拓扑优化方法，可兼顾可靠性与轻量化要求。可靠性概念-详细组合优化策略在简化布局并保证性能的同时，使加筋板结构材料成本降低21.40%。

关键词: 机械设计, 加筋板, 可靠性拓扑优化, 序列优化及可靠性评估算法, 混合均值法, 变密度法, 尺寸优化

Abstract:

For the three-dimensional stiffened plate， a non-nested reliability based topology optimization is proposed in order to achieve lightweight and engineering design while ensuring its safety and reliability. And the reliability concept-detailed combination optimization design is carried out for three-dimensional engineering stiffened plates. By virtue of the decoupling characteristics of the sequential optimization and reliability assessment method external optimization software with variable density method as the core was applied to carry out deterministic topology optimization to improve optimization efficiency. And considering the randomness of loads and materials， the hybrid mean value method was used to search the most probable point in the reliability evaluation stage. Furthermore， the layout of reliability conceptual design was interpreted and the size optimization was carried out to realize the engineering application. The result shows that compared with the deterministic topology optimization， the reliability topology optimization proposed in this paper can meet the requirements of structural reliability and lightweight. The combination optimization strategy of conceptual design and detailed design has realized that the engineering stiffened plate can reduce the material cost by 21.40% while simplifying the layout and ensuring the performance.

Key words: mechanical design, stiffened plate, reliability-based topology optimization, sequential optimization and reliability assessment method, hybrid mean value method, variable density method, size optimization

中图分类号:

P751

余建星,韦明秀,余杨,崔宇朋,潘宇. 加筋板结构可靠性拓扑优化与工程化设计[J]. 吉林大学学报(工学版), 2024, 54(10): 2781-2791.

Jian-xing YU,Ming-xiu WEI,Yang YU,Yu-peng CUI,Yu PAN. Reliability-based topology optimization and engineering design of stiffened plates[J]. Journal of Jilin University(Engineering and Technology Edition), 2024, 54(10): 2781-2791.

图/表 18

图1

图2

图3

图4

表1

图5

图6

表2

图7

表3

图8

图9

图10

图11

图12

表4

表5

图13

参考文献 19

1	Chu S, Featherston C, Kim H A. Design of stiffened panels for stress and buckling via topology optimization[J]. Structural and Multidisciplinary Optimization, 2021, 64: 3123-3146.
2	Li L, Liu C, Zhang W, et al. Combined model-based topology optimization of stiffened plate structures via MMC approach[J]. International Journal of Mechanical Sciences, 2021, 208: No.106682.
3	Wang Z, Yang C, Xu X, et al. Layout design of stiffened plates for large-scale box structure under moving loads based on topology optimization[J]. Mathematical Problems in Engineering, 2020(40): No.8843657.
4	Liu H, Li B, Yang Z, et al. Topology optimization of stiffened plate/shell structures based on adaptive morphogenesis algorithm[J]. Journal of Manufacturing Systems, 2017, 43: 375-384.
5	Dugré A, Vadean A, Chaussée J. Challenges of using topology optimization for the design of pressurized stiffened panels[J]. Structural and Multidisciplinary Optimization, 2016, 53: 303-320.
6	Perl M, Steiner M. 3-D stress intensity factors due to full autofrettage for inner radial or coplanar crack arrays and ring cracks in a spherical pressure vessel[J]. Engineering Fracture Mechanics, 2015, 138: 233-249.
7	崔宇朋, 余杨, 余建星, 等. 大跨度无支撑甲板拓扑-尺寸-材料联合优化设计[J]. 中国机械工程, 2022,33(23):2879-2897.
	Cui Yu-peng, Yu Yang, Yu Jian-xing, et al. Topology-size-material joint optimization design of long-span unsupported deck[J]. China Mechanical Engineering, 2022,33(23): 2879-2897.
8	曹迈, 王泽宇, 李全旺, 等. 基于SORA算法的混凝土结构尺寸优化[C]//第30届全国结构工程学术会议论文集, 广州,2021: 214-219.
9	李海燕, 井元伟. 基于SORA的多学科协同优化可靠性优化方法[J].东北大学学报:自然科学版, 2018, 39(1): 1-5.
	Li Hai-yan, Jing Yuan-wei. Multidisciplinary collaborative optimization reliability optimization method based on SORA[J]. Journal of Northeastern University (Natural Science) 2018, 39(1): 1-5.
10	胡新明, 王德禹.基于迭代均值组合近似模型和序贯优化与可靠性评估法的船舶结构优化设计[J].上海交通大学学报, 2017, 51(2): 150-156.
	Hu Xin-ming, Wang De-yu. Optimization design of ship structure based on iterative mean combination approximation model and sequential optimization and reliability evaluation method[J]. Journal of Shanghai Jiaotong University, 2017, 51(2): 150-156.
11	王宇, 余雄庆, 杜小平. 基于支持向量机的序列可靠性优化方法[J].计算力学学报, 2013, 30(4): 485-490.
	Wang Yu, Yu Xiong-qing, Du Xiao-ping. Sequence reliability optimization method based on support vector machine[J]. Journal of Computational Mechanics, 2013, 30(4): 485-490.
12	罗文俊, 王德禹. 基于兴趣子域动态代理模型的船舶结构可靠性优化[J].中国舰船研究, 2021, 16(4): 96-107.
	Luo Wen-jun, Wang De-yu. Reliability optimization of ship structure based on interest-based subdomain dynamic proxy model[J]. China Ship Research, 2021, 16(4): 96-107.
13	Deaton J D, Grandhi R V. A survey of structural and multidisciplinary continuum topology optimization: Post 2000[J]. Structural and Multidisciplinary Optimization, 2014, 49: 1-38.
14	Du X, Chen W. Sequential optimization and reliability assessment method for efficient probabilistic design[J]. J Mech Des, 2004, 126(2): 225-233.
15	Aoues Y, Chateauneuf A. Benchmark study of numerical methods for reliability-based design optimization[J]. Structural and Multidisciplinary Optimization, 2010, 41(2): 277-294.
16	Du X, Chen W. A most probable point-based method for efficient uncertainty analysis[J]. Journal of Design & Manufacturing Automation, 2001, 4(1):47-66.
17	Wu Y T, Millwater H R, Cruse T A. Advanced probabilistic structural analysis method for implicit performance functions[J]. AIAA Journal, 1990, 28(9):1663-1669.
18	Choi K K, Youn B D. Hybrid analysis method for reliability-based design optimization[J].Journal of Mechanical Design, 2003, 125(2): 221-232.
19	徐龙坤,何勇‍,金伟良.基于可靠度深海浮式平台加筋板优化设计方法[J].海洋工程,2010,28(3):17-23.
	Xu Long-kun, He Yong, Jin Wei-liang. Reliability-based design optimization for stiffened panel of deep-water platform[J]. The Ocean Engineering, 2010, 28(3):17-23.

相关文章 15

[1]	王琛,雒特,惠倩倩,王忠昊,王方方. 面向分体式飞行汽车对接锁定的机电系统设计与验证[J]. 吉林大学学报(工学版), 2024, 54(8): 2130-2140.
[2]	刘洋. 橡胶鞋底弹性打磨仿真及试验[J]. 吉林大学学报(工学版), 2024, 54(8): 2167-2173.
[3]	王磊,李东侠,周松,回丽,沈振鑫. 2024-O铝合金搅拌摩擦焊接头疲劳裂纹扩展行为及寿命预测[J]. 吉林大学学报(工学版), 2024, 54(6): 1563-1569.
[4]	刘洋,江涛. 计及安装角的六自由度平台虎克铰干涉计算模型[J]. 吉林大学学报(工学版), 2024, 54(6): 1519-1527.
[5]	谭晓丹,王勇澎,Hall Robert,徐天爽,黄庆学. 面向电铲自主装卸的矿用自卸车斗型优化[J]. 吉林大学学报(工学版), 2024, 54(5): 1227-1236.
[6]	王世俊,罗冠炜. 含多种碰撞约束振动系统的周期运动转迁特性[J]. 吉林大学学报(工学版), 2024, 54(4): 902-916.
[7]	孙伟,杨俊. 等角贴敷压电分流片圆柱壳有限元建模及减振分析[J]. 吉林大学学报(工学版), 2024, 54(2): 365-374.
[8]	胡斌,蔡一全,罗昕,毛自斌,李俊伟,郭孟宇,王剑. 基于种群胁迫的有限齿侧空间高速充种理论与试验[J]. 吉林大学学报(工学版), 2024, 54(2): 574-588.
[9]	王佳怡,刘昕晖,王展,陈晋市,韩亚方,王禹琪. 基于AMESim的恒流量控制阀流量特性分析[J]. 吉林大学学报(工学版), 2023, 53(9): 2499-2507.
[10]	程亚兵,杨泽宇,李岩,安立持,徐泽辉,曹鹏宇,陈璐翔. 基于混合动力汽车正时齿形链系统的振动噪声特性[J]. 吉林大学学报(工学版), 2023, 53(9): 2465-2473.
[11]	黄贤振,孙楷铂,栾晓刚,胡兵. 螺栓预紧连接可靠性灵敏度分析[J]. 吉林大学学报(工学版), 2023, 53(8): 2219-2226.
[12]	杨艳,侍玉青,张晓蓉,罗冠炜. 一类多刚性限幅振动系统的动态稳定性分析[J]. 吉林大学学报(工学版), 2023, 53(2): 364-375.
[13]	宋剑锋,黄鑫磊,仪帅,杨振熙,董永刚,李树林. 列车制动过程踏面温度场及应力⁃应变分布特性[J]. 吉林大学学报(工学版), 2023, 53(10): 2773-2784.
[14]	刘洋. 动臂塔机防后倾缓冲力计算方法[J]. 吉林大学学报(工学版), 2023, 53(10): 2785-2794.
[15]	刘洋. 动臂塔机卸载冲击仿真及试验[J]. 吉林大学学报(工学版), 2022, 52(6): 1292-1300.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

工况编号	工况描述	载荷	约束
1	面均布载荷	均布载荷0.015 MPa	四周简支
2	线均布载荷	两端线均布载荷250 N/mm	两端约束Z向位移
3	集中力载荷	中点和1/4中点处各2×10⁴N	四周简支

	μ	σ
弹性模量E	2.1×10⁵ MPa	2.1×10⁴
工况1面均布载荷p	0.015 MPa	0.01
工况2线均布载荷q	250 N/mm	25
工况3集中力载荷F	2.0×10⁴ N	2×10³

项目	工况1	工况2	工况3
可靠度指标β	3.0045	4.2649	3.8082
可靠概率	99.867%	99.999%	99.993%

梁编号	高度/mm	宽度/mm	梁编号	高度/mm	宽度/mm
1	1.584	1.569	17	50.000	1.500
2	1.725	1.613	18	50.000	1.506
3	50.000	5.961	19	50.000	43.830
4	4.349	3.442	20	2.443	2.686
5	4.246	4.314	21	6.002	5.086
6	3.710	3.620	22	4.635	2.844
7	4.322	3.879	23	3.452	3.341
8	3.563	3.313	24	50.000	1.503
9	7.389	4.303	25	50.000	2.868
10	3.534	4.357	26	11.113	2.010
11	2.155	1.709	27	50.000	1.523
12	4.159	2.788	28	50.000	2.710
13	4.403	4.417	29	50.000	2.330
14	3.765	3.959	30	47.260	3.153
15	50.000	35.39	31	1.858	1.678
16	3.595	1.353	32	50.000	34.750