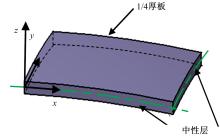
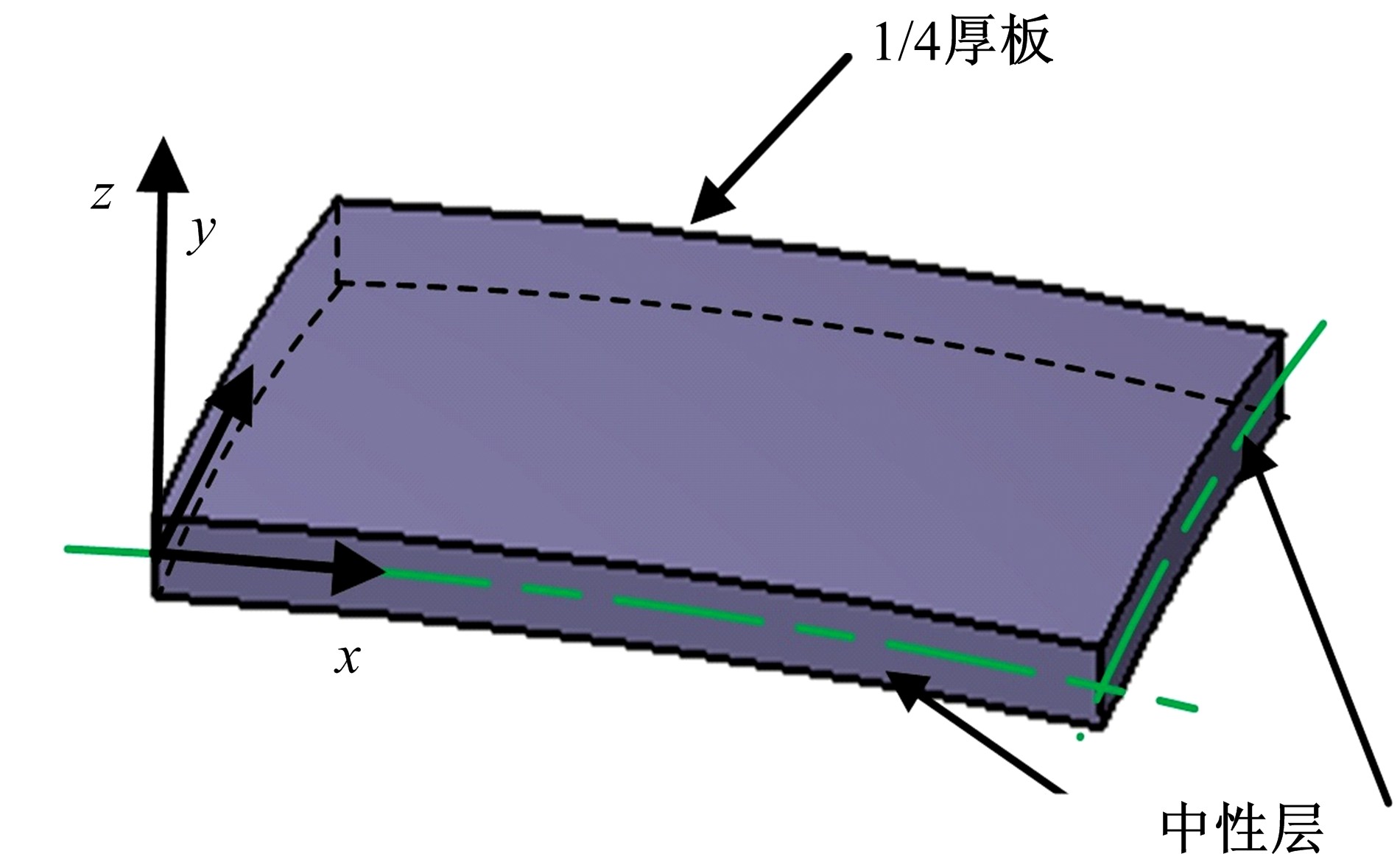
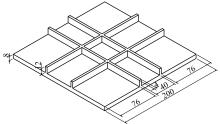
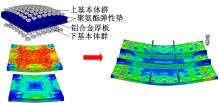
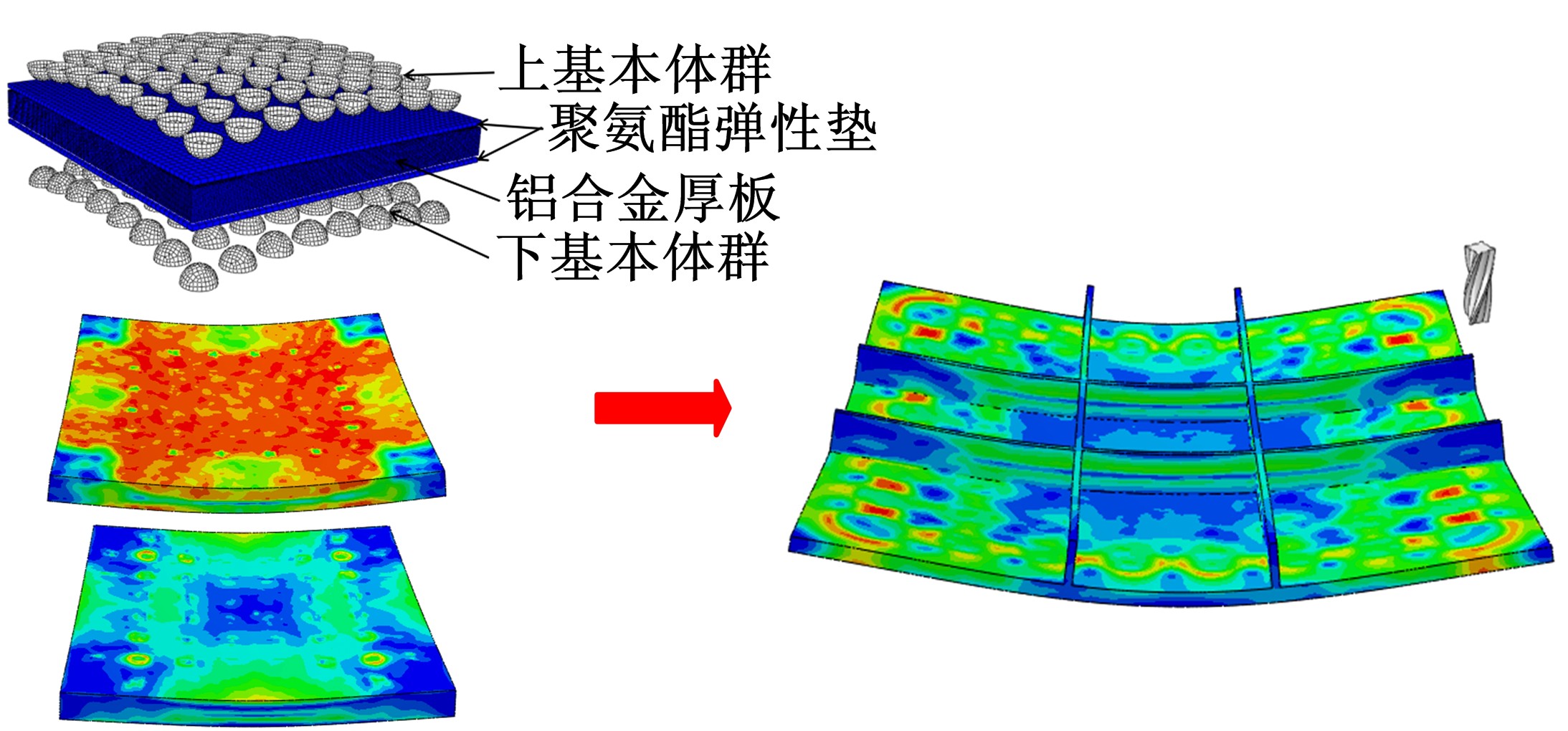
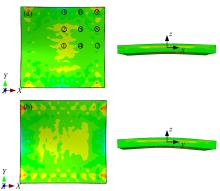
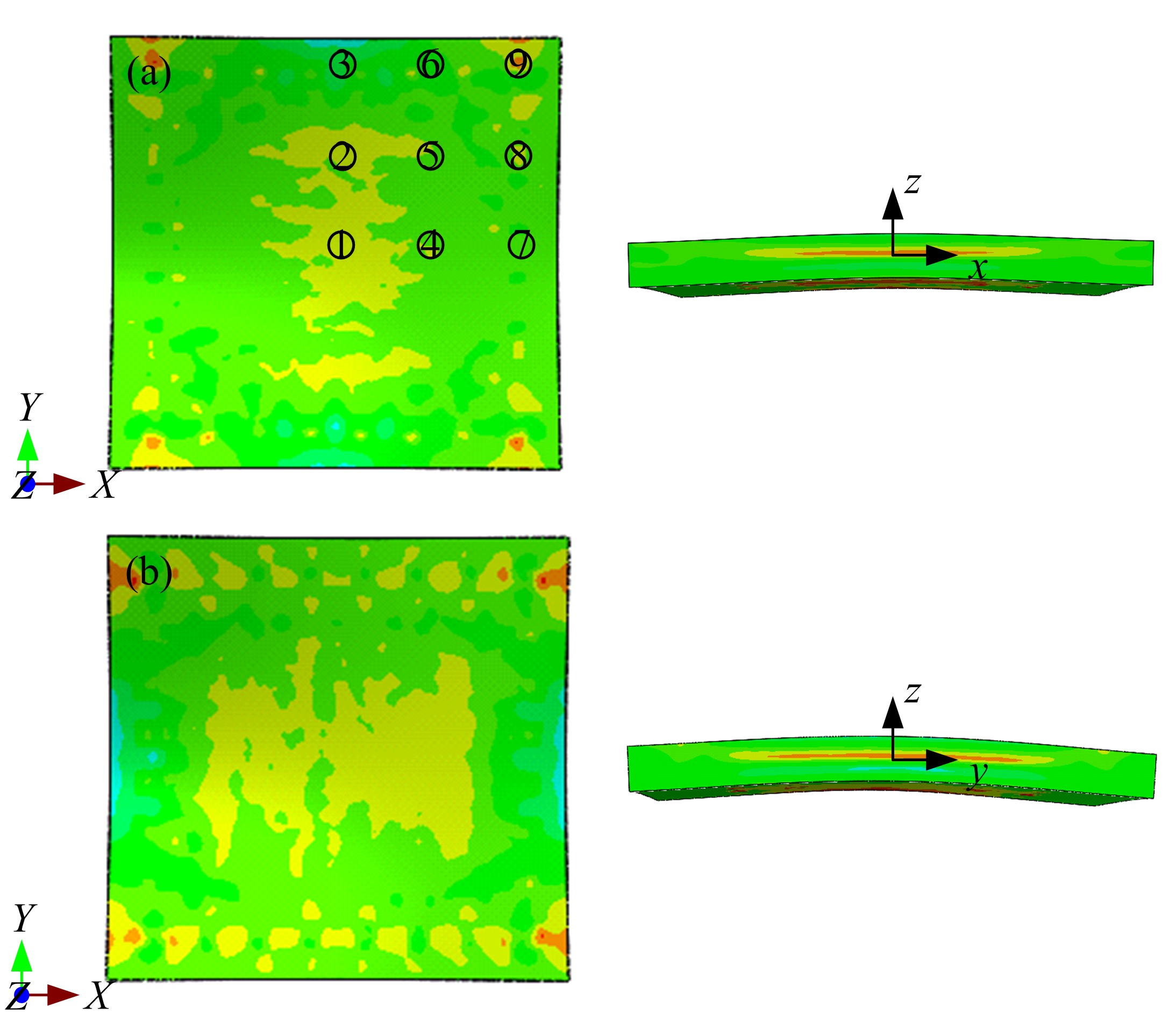
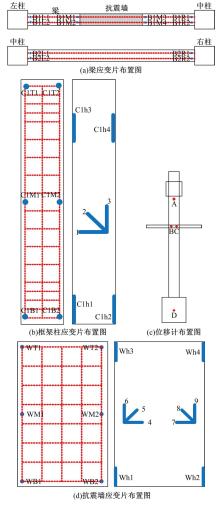
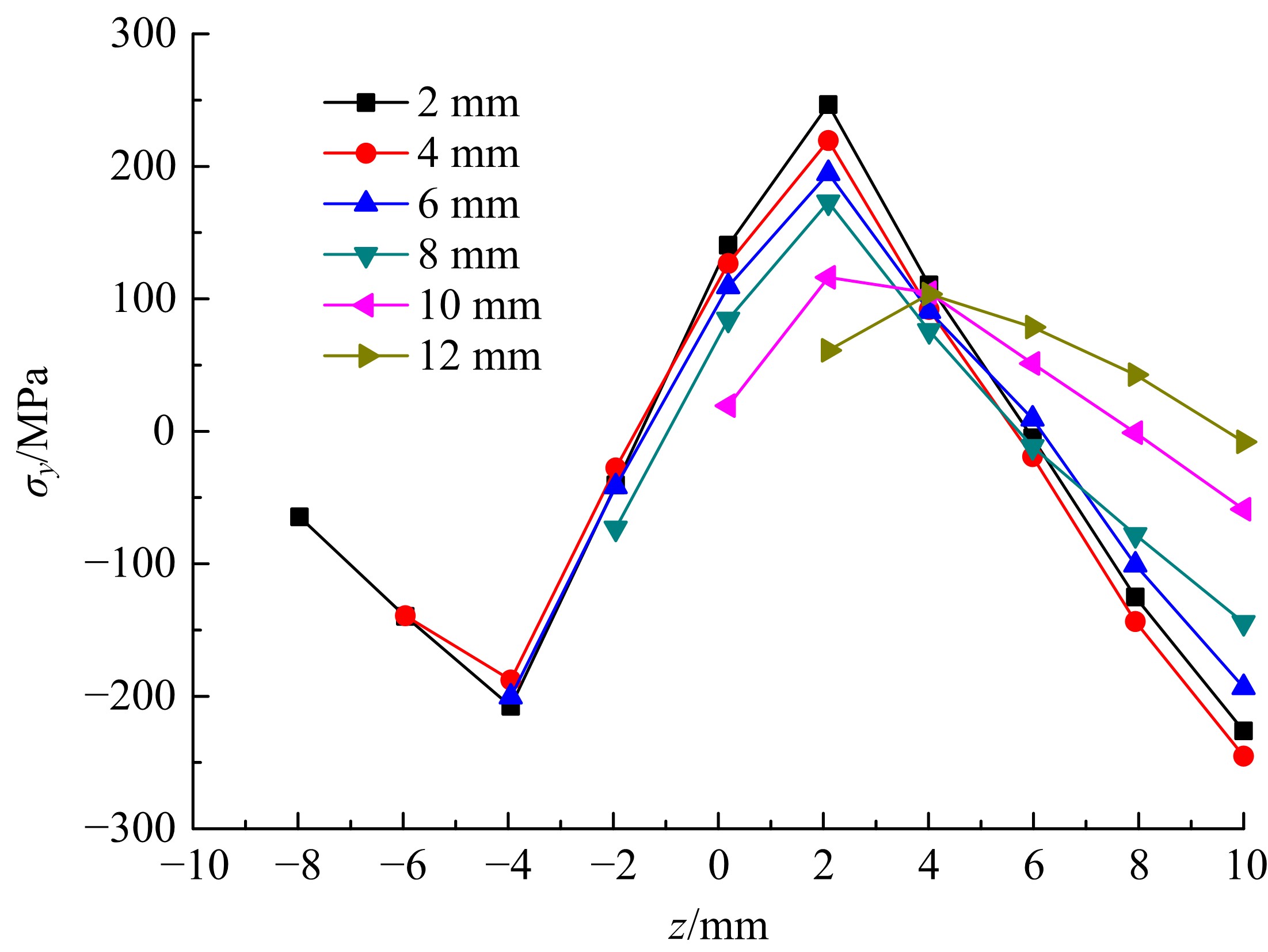
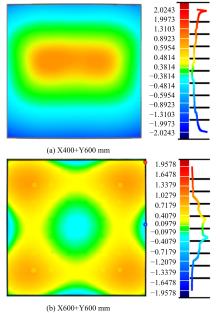
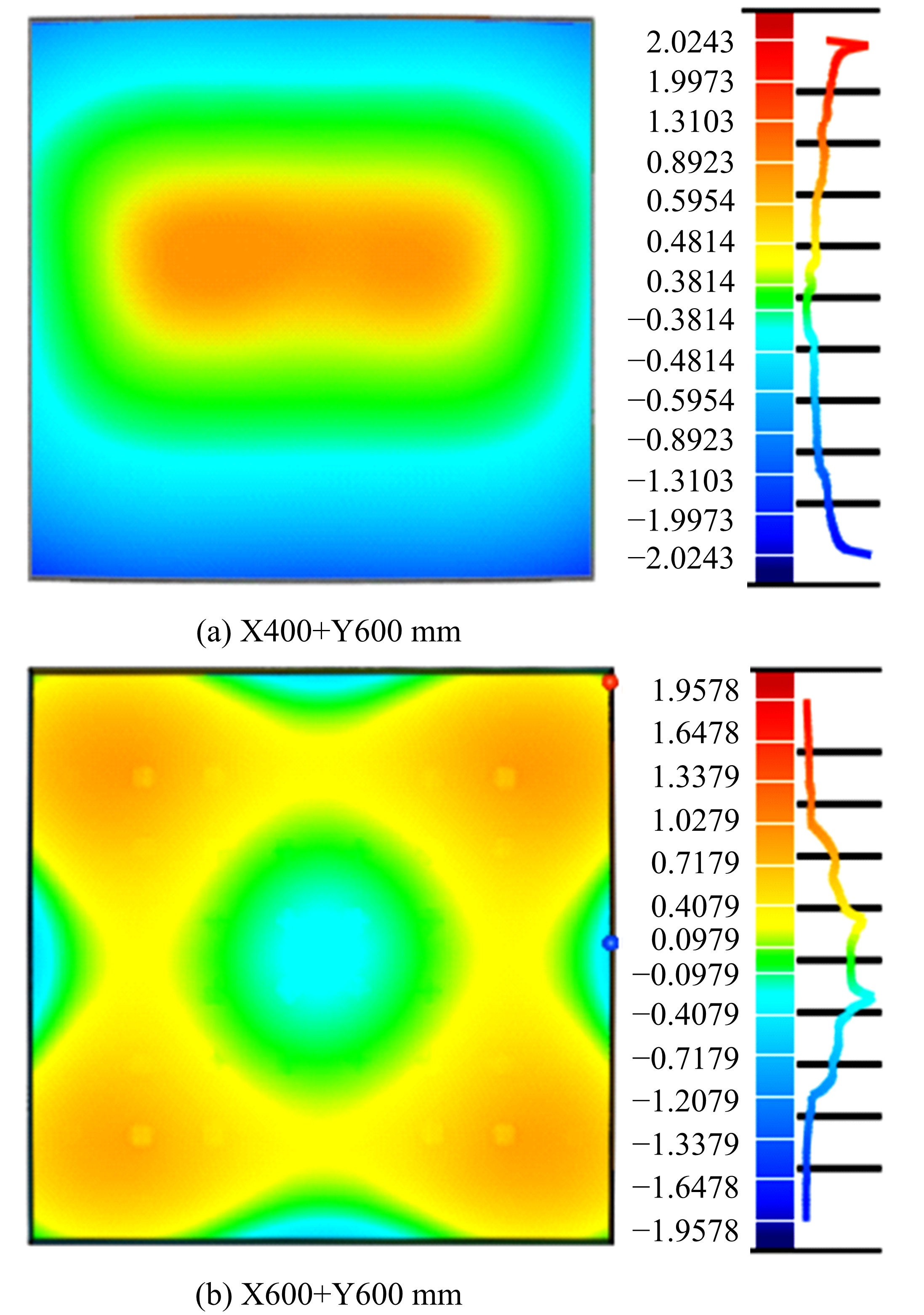
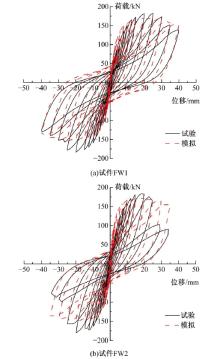
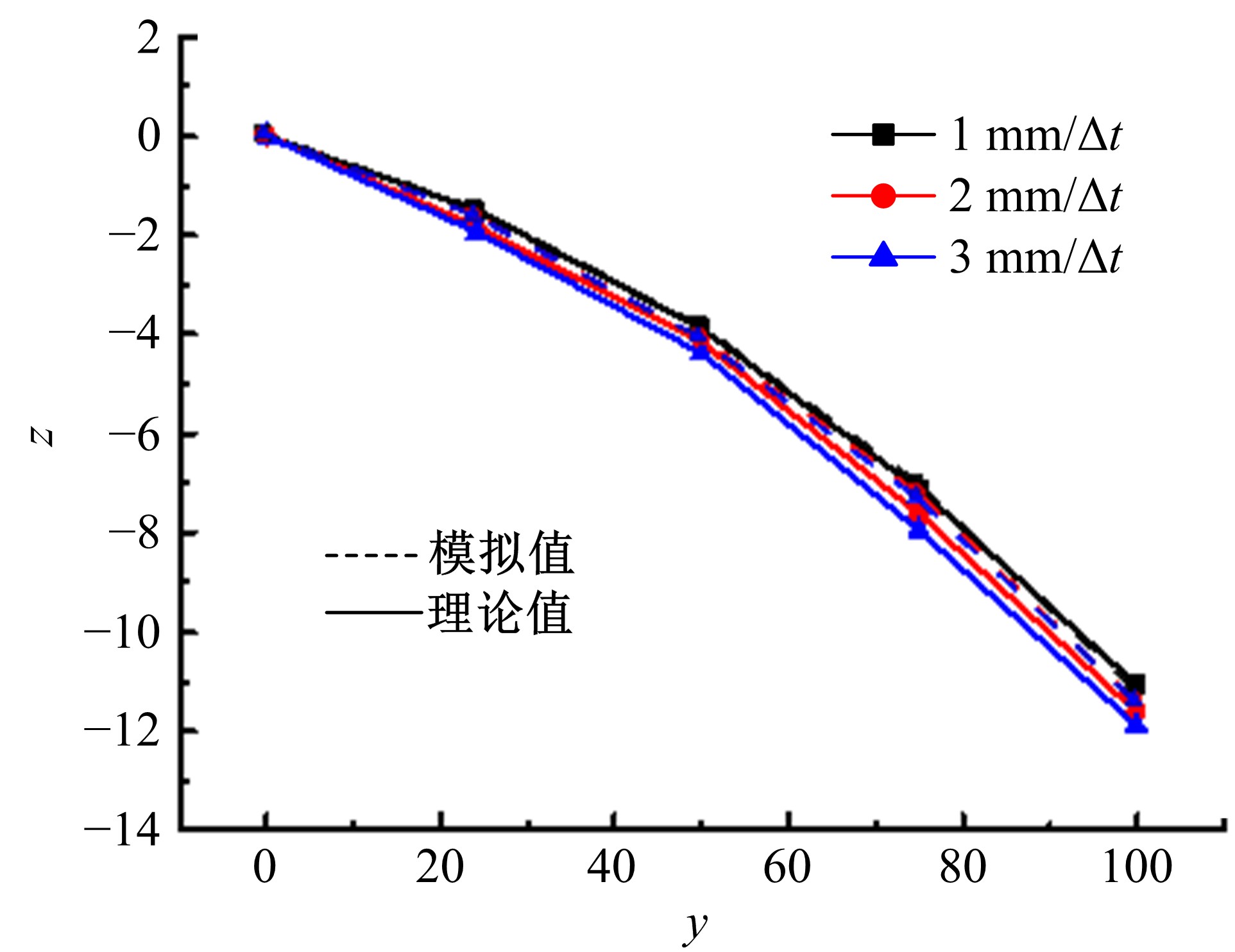
Journal of Jilin University(Engineering and Technology Edition) ›› 2021, Vol. 51 ›› Issue (1): 188-199.doi: 10.13229/j.cnki.jdxbgxb20190169

Previous Articles    

Springback prediction for double-curvature stiffened panel during milling

Chun-guo LIU1,2(),Xiao-tong YU1,2,Tao YUE1,2,Dong-lai LI1,2,Ming-zhe ZHANG1,2   

  1. 1.Roll-forging Research Institute，Jilin University，Changchun 130022，China
    2.College of Materials Science and Engineering，Jilin University，Changchun 130022，China
  • Received:2019-03-19 Online:2021-01-01 Published:2021-01-20

RICH HTML

 4   

PDF (PC)

89

Abstract:

Aiming at the springback problem during manufacturing process of aluminum alloy thin-walled parts， a springback prediction method for double-curvature stiffened panel in milling process was proposed. The method estimates the springback value in the two directions of the panel according to the redistribution of the residual stress after the material is removed layer by layer. The finite element simulation results show that the stress distribution and radius after springback of the panel during the milling process were close to the calculated results. The maximum stress variation in both directions appears when the milling depth reaches the initial neutral surface. When the remaining thickness decreases， the errors between calculation results and FEM results increase gradually. In addition， the simulation results of different single-layer milling thickness show that the larger the thickness of single-layer milling， the larger the error of this method， and the maximum error is 9.07%. The forming-milling experiments were performed to verify the proposed method. The results show that the proposed method could predict the springback of the double-curvature stiffened panel.

Key words: double-curvature panel, springback prediction, residual stress, finite element method（FEM）

CLC Number: 

  • TG386

Fig.1

Schematic diagram of computing model"

Fig.2

Schematic diagram of aluminum alloy panel"

Fig.3

Finite element model of bending-milling"

Fig.4

Bending-milling experiment"

Fig.5

Location of point selected"

Fig.6

Stress distribution in every layers of point selected"

Fig.7

Distribution of residual stress of sheet after bending"

Fig.8

Distribution of σx along the z-axis of sheet after milling"

Fig.9

Distribution of σy along the z-axis of sheet after milling"

Fig.10

Selecting position of springback path in milling"

Fig.11

Milling springback curve"

Fig.12

Comparison of error between finite element and calculation results with different bending radii"

Fig.13

Comparison of error between experiment and calculation results with different bending radii"

Fig.14

Distribution of σx along the z-axis after removal of 12 mm from sheet"

Fig.15

Springback error between calculation and finite element results of the panels for different single-layer milling thicknesses"

Fig.16

Comparison of error between finite element and calculation results with different thickness of stiffener"

1 曾元松, 黄遐. 大型整体壁板成形技术[J]. 航空学报, 2008, 29(3): 721-727.
Zeng Yuan-song, Huang Xia. Forming technologies of large integral panel[J]. Acta Aeronautica Et Astronautica Sinica, 2008, 29(3): 721-727.
2 董亚男. 铝合金整体板多点冲压成形断裂的预测与控制[D]. 长春:吉林大学材料科学与工程学院, 2016.
Dong Ya-nan. Prediction and control of fracture in multi-point press forming of aluminum alloy integral panel[D]. Changchun: College of Materials Science and Engineering, Jilin University, 2016.
3 刘纯国, 岳韬, 邓玉山, 等. 一种高筋铝合金壁板制造方法[P]. 中国: 201610634093, 2016-10-26.
4 Rossini N S, Dassisti M, Benyounis K Y, et al. Methods of measuring residual stresses in components[J]. Materials & Design, 2012, 35(1): 572-588.
5 Sebastiani M, Eberl C, Bemporad E, et al. Focused ion beam four-slot milling for poisson's ratio and residual stress evaluation at the micron scale[J]. Surface and Coatings Technology, 2014(251): 151-161.
6 Liu C G, Zheng Y, Zhang X G. Investigation of through thickness residual stress distribution and springback in bent AL plate by slotting method[J]. The International Journal of Advanced Manufacturing Technology, 2017, 90(1-4): 299-308.
7 Meng L, Atli M, He N. Measurement of equivalent residual stresses generated by milling and corresponding deformation prediction[J]. Precision Engineering, 2017, 50: 160-170.
8 Shin S H. Prediction of the dimensional instability resulting from machining of residually stressed components[D]. Lubbock:Texas Tech University, 1995.
9 Wang S, Zuo D, Wang M, et al. Modified layer removal method for measurement of residual stress distribution in thick pre-stretched aluminum plate[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2004, 21(4): 286-290.
10 Sebastian N. A mathematical model for the estimation of the effects of residual stresses in aluminum plates[D]. City of Saint Louis: Washington University in St. Louis, 2005.
11 Yong K A. Machining-induced residual stress and distortion of thin parts[D]. City of Saint Louis: Washington University in St. Louis, 2005.
12 Wu Q, Li D P, Ren L, et al. Detecting milling deformation in 7075 aluminum alloy thin-walled plates using finite difference method[J]. The International Journal of Advanced Manufacturing Technology, 2016, 85(5-8): 1291-1302.
13 Wei Y, Wang X W. Computer simulation and experimental study of machining deflection due to original residual stress of aerospace thin-walled parts[J]. The International Journal of Advanced Manufacturing Technology, 2007, 33(3/4): 260-265.
14 Tang Z T, Yu T, Xu L Q, et al. Machining deformation prediction for frame components considering multifactor coupling effects[J]. The International Journal of Advanced Manufacturing Technology, 2013, 68(1-4): 187-196.
15 Izamshah R, Mo J P T, Ding S. Hybrid deflection prediction on machining thin-wall monolithic aerospace components[J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2012, 226(4): 592-605.
16 孙杰, 柯映林. 残余应力对航空整体结构件加工变形的影响分析[J]. 机械工程学报, 2005, 41(2): 117-122.
Sun Jie, Ke Ying-lin. Study on machining distortion of unitization airframe due to residual stress[J]. Chinese Journal of Mechanical Engineering, 2005, 41(2): 117-122.
17 Li W, Ma L, Wan M, et al. Modeling and simulation of machining distortion of pre-bent aluminum alloy plate[J]. Journal of Materials Processing Technology, 2018, 258: 189-199.
18 Gao H, Zhang Y, Wu Q, et al. Investigation on influences of initial residual stress on thin-walled part machining deformation based on a semi-analytical model[J]. Journal of Materials Processing Technology, 2018, 262: 437-448.
19 余同希, 章亮炽. 塑性弯曲理论及其应用[M]. 北京: 科学出版社, 1992.
20 Adibi H, Asadian Ardakani M H, Mollaei Dariani B. Springback analysis of sheet metal laminates after U-bending[C]∥The 19th International Conference on Metallurgy and Materials, Roznov pod Radhostem, Czech Republic, 2010.
21 林胜. HSM在航空制造业中的应用[J].航空制造技术, 2003(3): 25-28, 76.
Lin Sheng. HSM application in aviation manufacturing industry [J]. Aeronautical Manufacturing Technology, 2003(3): 25-28, 76.
22 Li B, Jiang X, Yang J, et al. Effects of depth of cut on the redistribution of residual stress and distortion during the milling of thin-walled part[J]. Journal of Materials Processing Technology, 2015, 216: 223-233.
[1] Jin⁃zhong LU,Wan⁃ting ZHOU,Sheng⁃yang ZHANG,Yi⁃kai SHAO,Chang⁃yu WANG,Kai⁃yu LUO. Effect of coverage layer on corrosion resistance of 6061⁃T6 aluminum alloy subjected to laser shock peening [J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(3): 842-849.
[2] LIU Zi-wu, LI Jian-feng. Erosion damage and evaluation of remanufacturing cladding layer for impeller metals FV520B [J]. 吉林大学学报(工学版), 2018, 48(3): 835-844.
[3] LIU Yu, LI Peng-fei, ZHANG Yi-min. Analysis and prediction of micro milling deformation of copper thin-wall parts [J]. 吉林大学学报(工学版), 2017, 47(3): 844-849.
[4] LIANG Ji-cai, LI Yi, GAO Song, TENG Fei. Springback prediction for multi-point 3D stretch bending profile [J]. 吉林大学学报(工学版), 2017, 47(1): 185-190.
[5] ZHUANG Ye, CHEN Yu-hang, YANG Ye-hai, XU Shu-fang. Twin-tube hydraulic shock absorber F-V modeling based on structure parameters [J]. 吉林大学学报(工学版), 2016, 46(3): 732-736.
[6] MA Yao, DONG Xiao-long, LI Ze-jun, SHEN Lin, ZHAO Hong-wei. Finite element simulation of the effect of different initial contact on nano-indentation [J]. 吉林大学学报(工学版), 2014, 44(5): 1366-1370.
[7] PENG Yong, SUN Li-jun. Numerical simulation of effect of horizontal aggregate distribution in asphalt mixtures on splitting test [J]. 吉林大学学报(工学版), 2013, 43(04): 891-896.
[8] WANG Yong-hua, ZHANG Cheng-chun, WANG Jing, SHI Lei, ZHANG Xue-peng, REN Lu-quan. Analysis of sound-absorbing performance of bionic porous material [J]. , 2012, (06): 1442-1447.
[9] YAN Qing-dong, CUI Hong-wei, WEI Wei. Finite element analysis of blade wheel strength in hydrodynamic tractor-retarder assembly under traction condition [J]. 吉林大学学报(工学版), 2012, 42(02): 365-371.
[10] MIAO Hong, ZUO Dun-wen, WANG Min, ZHANG Rui-hong, WANG Hong-feng. Effect of technological parameters on quality of Q460 high-strength-steel internal thread formed by cold extrusion [J]. 吉林大学学报(工学版), 2012, 42(01): 68-73.
[11] KONG De-jun, ZHOU Chao-zheng, HU Ai-ping. Effect of laser shock on the mechanical properties of weld joint of X70 steel pipeline [J]. 吉林大学学报(工学版), 2011, 41(05): 1507-1512.
[12] ZHANG Jin-Le, MA Biao, ZHANG Ying-Feng, LI He-Yan. Simulation of thermal characteristic of wet shift clutch [J]. 吉林大学学报(工学版), 2011, 41(02): 321-0326.
[13] SHI Yong-Jiu, YANG Lu, WANG Yuan-Qing, LI Qiu-Zhe. Bending stiffness of composite slim beam with deep deck [J]. 吉林大学学报(工学版), 2010, 40(06): 1550-1555.
[14] LI Jie, QIN Yu-Ying, ZHAO Qi. Modelling and simulation of fullvehicle random vibration [J]. 吉林大学学报(工学版), 2010, 40(02): 316-0319.
[15] LUO Kai-Yu, LU Jin-Zhong, YIN Chun-Jing, ZHONG Jun-Wei, YAO Hui-Xue, ZHANG Yong-Kang. Properties of LY2 alloy film by laser shock processing [J]. 吉林大学学报(工学版), 2010, 40(02): 467-0470.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
Copyright © Journal of Jilin University(Engineering and Technology Edition), All Rights Reserved.
Tel: +86-431-85095297　Fax: +86-431-85094074　E-mail: xbgxb@jlu.edu.cn
Powered by Beijing Magtech Co. Ltd