吉林大学学报(工学版) ›› 2019, Vol. 49 ›› Issue (4): 1144-1152.doi: 10.13229/j.cnki.jdxbgxb20180020
• • 上一篇
聚丙烯纤维增强混凝土断裂韧度及软化本构曲线确定
梁宁慧1,2( ),缪庆旭1,2,刘新荣1,2,代继飞3,钟祖良1,2
),缪庆旭1,2,刘新荣1,2,代继飞3,钟祖良1,2
- 1. 重庆大学 土木工程学院, 重庆 400045
2. 库区环境地质灾害防治国家地方联合工程研究中心, 重庆 400045
3. 中国建设基础设施有限公司, 北京 100044
Determination of fracture toughness and softening traction⁃separation law of polypropylene fiber reinforced concrete
Ning⁃hui LIANG1,2( ),Qing⁃xu MIAO1,2,Xin⁃rong LIU1,2,Ji⁃fei DAI3,Zu⁃liang ZHONG1,2
),Qing⁃xu MIAO1,2,Xin⁃rong LIU1,2,Ji⁃fei DAI3,Zu⁃liang ZHONG1,2
- 1. School of Civil Engineering, Chongqing University, Chongqing 400045, China
2. National Joint Engineering Research Center of Geohazards Prevention in the Reservoir Areas, Chongqing 400045, China
3. China Construction Infrastructure Co, Ltd, Beijing 100044, China
摘要:
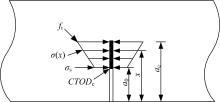
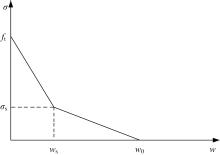
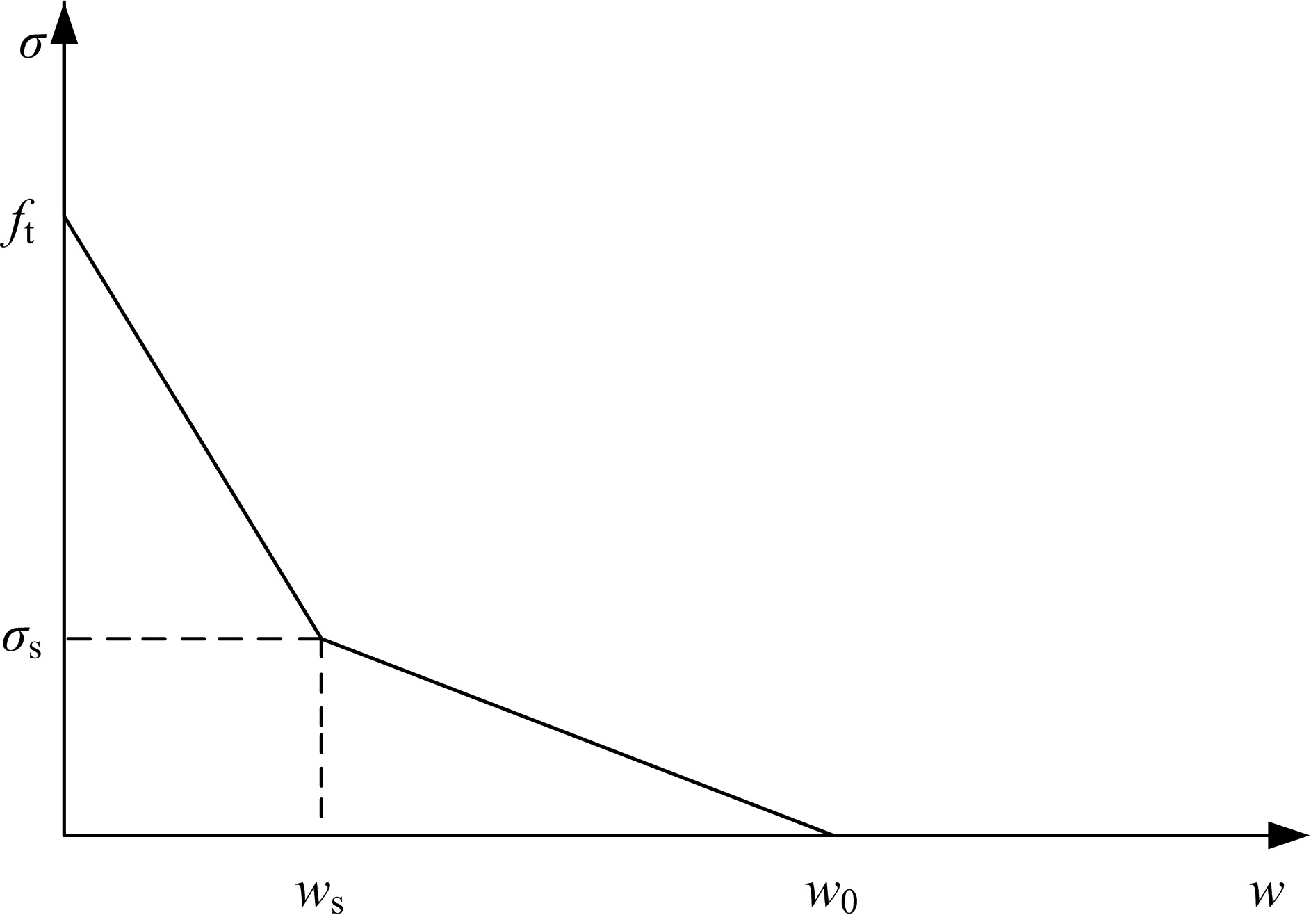
对粗、细聚丙烯(Polypropylene, PP)纤维不同混掺情况下的混凝土切口梁试件进行三点弯曲试验,基于双K断裂理论探讨了不同尺寸PP纤维混掺方式对试件断裂韧度的影响及其破坏机理,并通过起裂、失稳、黏聚韧度3者之间的定量关系得到实测黏聚韧度、起裂韧度增量和桥接韧度。借鉴3种普通混凝土的双线性软化本构曲线计算得到理论黏聚韧度,并将其与实测黏聚韧度对比,确定适合于不同纤维掺入情况下PP纤维增强混凝土(Polypropylene fiber reinforced concrete, PFRC)的双线性软化本构曲线。研究结果表明,PFRC相对素混凝土有较高的起裂韧度、失稳韧度和断裂能;2或3种尺寸PP纤维混掺时,其桥接应力对桥接韧度的增强效果非常显著;3种尺寸PP纤维在裂缝扩展的不同阶段发挥桥接作用,体现了良好的混掺增强、增韧效应;徐世烺和Reinhardt改进的双线性软化本构曲线,取校正系数λ为6时,可较好地适用于PFRC。
中图分类号:
- TU528
| 1 | Xu T , Stewart R , Fan J , et al . Bridging crack propagation at the atomistic and mesoscopic scale for BCC⁃Fe with hybrid multiscale methods[J]. Engineering Fracture Mechanics, 2016, 155: 166⁃182. |
| 2 | Liang N , Dai J , Liu X . Study on tensile damage constitutive model for multiscale polypropylene fiber concrete[J]. Advances in Materials Science and Engineering, 2016, 9168984. |
| 3 | 邓宗才 . 混杂纤维增强超高性能混凝土弯曲韧性与评价方法[J]. 复合材料学报, 2016, 33(6):1274⁃1280. |
| Deng Zong⁃cai . Flexural toughness and character⁃ization method of hybrid fibers reinforced ultra⁃high performance concrete[J]. Acta Materiae Compositae Sinica, 2016, 33(6): 1274⁃1280. | |
| 4 | 夏冬桃, 刘向坤, 夏广政, 等 . 混杂纤维增强高性能混凝土弯曲韧性研究[J]. 华中科技大学学报: 自然科学版, 2013, 41(6): 108⁃112. |
| Xia Dong⁃tao , Liu Xiang⁃kun , Xia Guang⁃zheng , et al . Flexural toughness of high⁃performance hybrid fiber reinforced concrete[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2013, 41(6): 108⁃112. | |
| 5 | Caggiano A , Gambarelli S , Martinelli E , et al . Experimental characterization of the post⁃cracking response in hybrid steel/polypropylene fiber⁃ reinforced concrete[J]. Construction & Building Materials, 2016, 125:1035⁃1043. |
| 6 | 陆洲导, 俞可权 . 高温后混凝土断裂韧度及软化本构曲线确定[J]. 同济大学学报:自然科学版, 2012, 40(9): 1306⁃1311. |
| Lu Zhou⁃dao , Yu Ke⁃quan . Determination of residual fracture toughness and softening traction⁃separation law of post⁃fire concrete[J]. Journal of Tongji University (Nature Science), 2012, 40(9): 1306⁃1311. | |
| 7 | Xu S L . Determination of parameters in the bilinear, Reinhardt’s and exponentially nonlinear softening curves and their physical meaning[C]∥Werkstoffe und Werkstoffprüfung im Bauwesen, Hamburg,Libri BOD,1999: 410⁃424. |
| 8 | 徐世烺, 熊松波, 李贺东, 等 . 混凝土断裂参数厚度尺寸效应的定量表征与机理分析[J]. 土木工程学报, 2017, 50(5): 57⁃71. |
| Xu Shi⁃lang , Xiong Song⁃bo , Li He⁃dong , et al . Quantitative characterization and mechanism analysis on thickness⁃dependent size effect of concrete fracture[J]. China Civil Engineering Journal, 2017, 50(5): 57⁃71. | |
| 9 | Amin A , Foster S J , Muttoni A . Derivation of the σ‐w relationship for SFRC from prism bending tests[J]. Structural Concrete, 2015, 16(1): 93⁃105. |
| 10 | Li D S , Hai C , Ou J . Fracture behavior and damage evaluation of polyvinyl alcohol fiber concrete using acoustic emission technique[J]. Materials & Design, 2012, 40: 205⁃211. |
| 11 | Almusallam T , Ibrahim S M , Al⁃Salloum Y , et al . Analytical and experimental investigations on the fracture behavior of hybrid fiber reinforced concrete[J]. Cement & Concrete Composites, 2016, 74: 201⁃217. |
| 12 | Dong W , Wu Z , Zhou X , et al . A comparative study on two stress intensity factor⁃based criteria for prediction of mode⁃I crack propagation in concrete[J]. Engineering Fracture Mechanics, 2016, 158:39⁃58. |
| 13 | Kazemi M T , Golsorkhtabar H , Beygi M H A , et al . Fracture properties of steel fiber reinforced high strength concrete using work of fracture and size effect methods[J]. Construction & Building Materials, 2017, 142: 482⁃489. |
| 14 | Tada H , Paris P C , Irwin G R . The Stress Analysis of Cracks Handbook[M]. New York:Wiley,2000. |
| 15 | 陈江义, 刘保元 . 纤维断裂损伤对复合材料板中导波频散特性的影响[J]. 吉林大学学报:工学版, 2017, 47(1): 180⁃184. |
| Chen Jiang⁃yi , Liu Bao⁃yuan . Influence of fiber fracture damage on dispersion characteristic of guided wave in composite plate[J]. Journal of Jilin University(Engineering and Technology Edition), 2017, 47(1): 180⁃184. | |
| 16 | Peterson P E . Crack Growth and Development of Fracture Zone in Plane Concrete and Similar Materials[M]. Lund: Division of Building Materials, 1981. |
| 17 | CEB. CEB⁃FIP model code 1990, Bulletin D information, No,213/214[S]. |
| 18 | Reinhardt H W , Xu S . Crack extension resistance based on the cohesive force in concrete[J]. Engin eering Fracture Mechanics, 1999, 64(5): 563⁃587. |
| 19 | Awinda K , Chen J , Barnett S J . Investigating geometrical size effect on the flexural strength of the ultra high performance fiber reinforced concrete using the cohesive crack model[J]. Construction & Building Materials, 2016, 105: 123⁃131. |
| 20 | 赵艳华, 聂玉强, 徐世烺 . 混凝土断裂能的边界效应确定法[J]. 工程力学, 2007, 24(1): 56⁃61. |
| Zhao Yan⁃hua , Nie Yu⁃qiang , Xu Shi⁃lang . Deter⁃mination of boundary effect on fracture of concrete[J]. Engineering Mechanics, 2007, 24(1): 56⁃61. |
| [1] | 张磊,刘保国,储昭飞. 深厚孔隙砂岩含水层疏干排水对盾构斜井的 影响模型试验[J]. 吉林大学学报(工学版), 2019, 49(3): 788-797. |
| [2] | 郑一峰, 赵群, 暴伟, 李壮, 于笑非. 大跨径刚构连续梁桥悬臂施工阶段抗风性能[J]. 吉林大学学报(工学版), 2018, 48(2): 466-472. |
| [3] | 王腾, 周茗如, 马连生, 乔宏霞. 基于断裂理论的湿陷性黄土劈裂注浆裂纹扩展[J]. 吉林大学学报(工学版), 2017, 47(5): 1472-1481. |
| [4] | 郭楠, 张平阳, 左煜, 左宏亮. 竹板增强胶合木梁受弯性能[J]. 吉林大学学报(工学版), 2017, 47(3): 778-788. |
| [5] | 张静, 刘向东. 混沌粒子群算法优化最小二乘支持向量机的混凝土强度预测[J]. 吉林大学学报(工学版), 2016, 46(4): 1097-1102. |
| [6] | 郭学东, 马立军, 张云龙. 集中力作用下考虑剪切滑移效应的双层结合面组合梁解析解[J]. 吉林大学学报(工学版), 2016, 46(2): 432-438. |
| [7] | 赵玉, 李衍赫, 张培, 赵科, 刘伟超. 粘土的动力特性试验[J]. 吉林大学学报(工学版), 2015, 45(6): 1791-1797. |
| [8] | 侯忠明, 王元清, 夏禾, 张天申. 移动荷载作用下的钢-混简支结合梁动力响应[J]. 吉林大学学报(工学版), 2015, 45(5): 1420-1427. |
| [9] | 王甲春, 阎培渝. 海洋环境下钢筋混凝土中钢筋锈蚀的概率[J]. 吉林大学学报(工学版), 2014, 44(2): 352-357. |
| [10] | 张大山, 董毓利, 吴亚平. 混凝土单向板的受拉薄膜效应计算[J]. 吉林大学学报(工学版), 2013, 43(05): 1253-1257. |
| [11] | 柴寿喜, 王沛, 魏丽. 以峰值轴向应变评价麦秸秆和石灰加筋固化盐渍土的抗变形性能 [J]. , 2012, (03): 645-650. |
| [12] | 李春良, 王国强, 赵凯军, 朱春凤. 地面荷载作用盾构隧道纵向力学行为[J]. 吉林大学学报(工学版), 2011, 41(增刊2): 180-184. |
| [13] | 潘明远, 姚继涛. 钢筋混凝土结构构件的可靠性[J]. 吉林大学学报(工学版), 2010, 40(增刊): 218-0221. |
| [14] | 郑文忠, 万夫雄, 李时光. 用无机胶粘贴CFRP布加固混凝土板火灾后受力性能[J]. 吉林大学学报(工学版), 2010, 40(05): 1244-1249. |
| [15] | 王刚,王清湘,刘士润. 钢筋混凝土板的压力膜效应承载力计算方法[J]. 吉林大学学报(工学版), 2010, 40(03): 699-0704. |
|
||