吉林大学学报(工学版) ›› 2019, Vol. 49 ›› Issue (4): 1153-1161.doi: 10.13229/j.cnki.jdxbgxb20180174

• • 上一篇    

超高强钢筋工程用水泥基复合材料梁受弯计算理论

李碧雄1,2(),廖桥1,2,章一萍3,4,周练3,4,隗萍3,4,刘侃1,2   

  1. 1. 四川大学 建筑与环境学院，成都 610065
    2. 四川大学 深地科学与工程教育部重点实验室，成都 610065
    3. 四川省建筑设计研究院，成都 610072
    4. 四川省建筑工业化工程技术研究中心，成都 610072
  • 收稿日期:2018-02-28 出版日期:2019-07-01 发布日期:2019-07-16
  • 作者简介:李碧雄（1970?），女，教授，博士. 研究方向：工程用水泥基复合材料. E?mail:libix@126.com
  • 基金资助:
    国家自然科学基金项目(51678379);四川省学术带头人培养基金项目(川人社办发[2016]183-2);国家重点研发计划项目(2018YFC1508802_01-02)

Theoretical on flexural behavior of ultra high strength rebar reinforced engineered cementitious composites beam

Bi⁃xiong LI1,2(),Qiao LIAO1,2,Yi⁃ping ZHANG3,4,Lian ZHOU3,4,Ping WEI3,4,Kan LIU1,2   

  1. 1. College of Architecture and Environment, Sichuan University, Chengdu 610065, China
    2. Key Laboratory of Deep Underground Science and Engineering for Ministry of Education, Sichuan University, Chengdu 610065, China
    3. Sichuan Provincial Architectural Design and Research Institute, Chengdu 610072, China
    4. Sichuan Engineering and Technology Research Center of Architecture Industrialization, Chengdu 610072, China
  • Received:2018-02-28 Online:2019-07-01 Published:2019-07-16

RICH HTML

 2   

PDF (PC)

83

摘要：

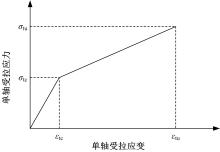
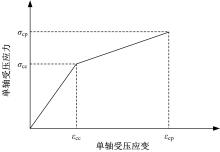
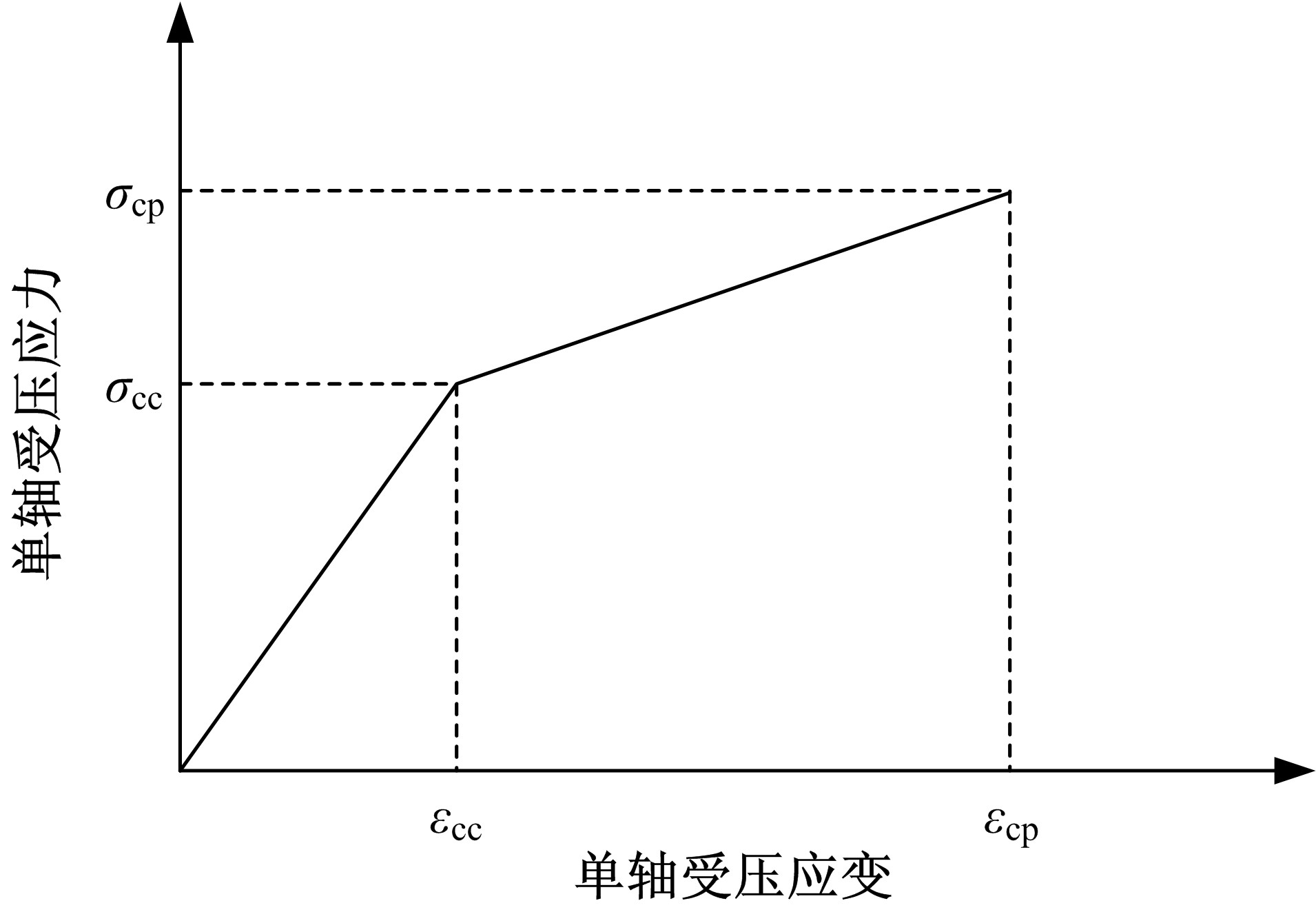
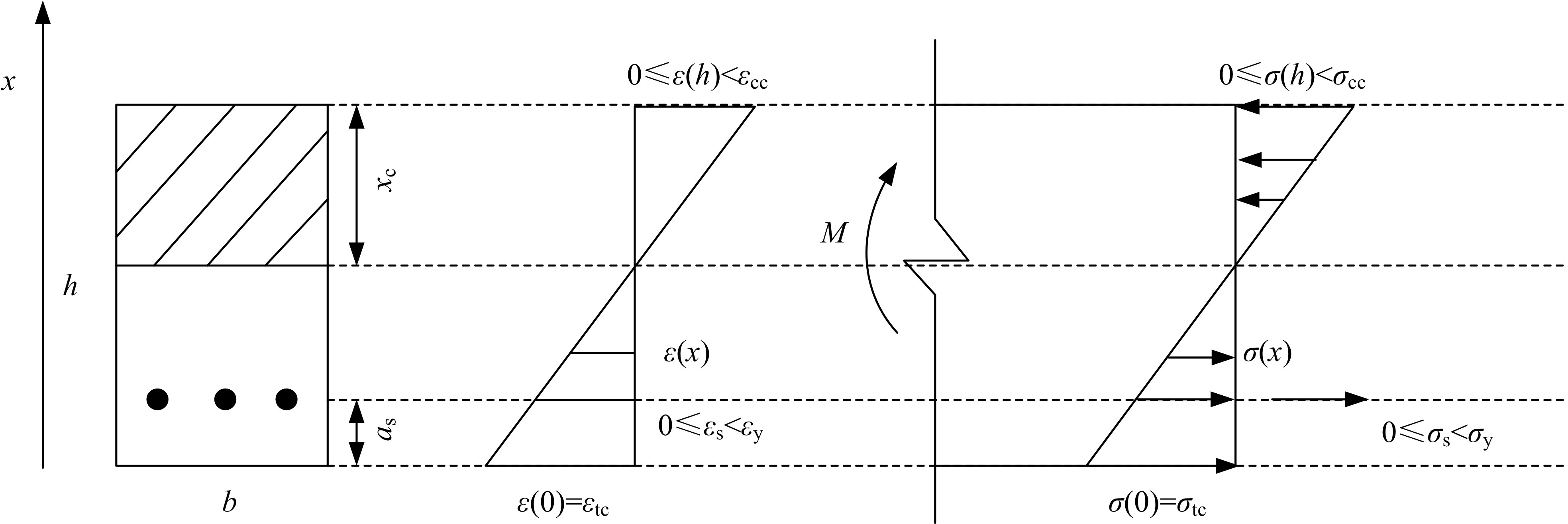
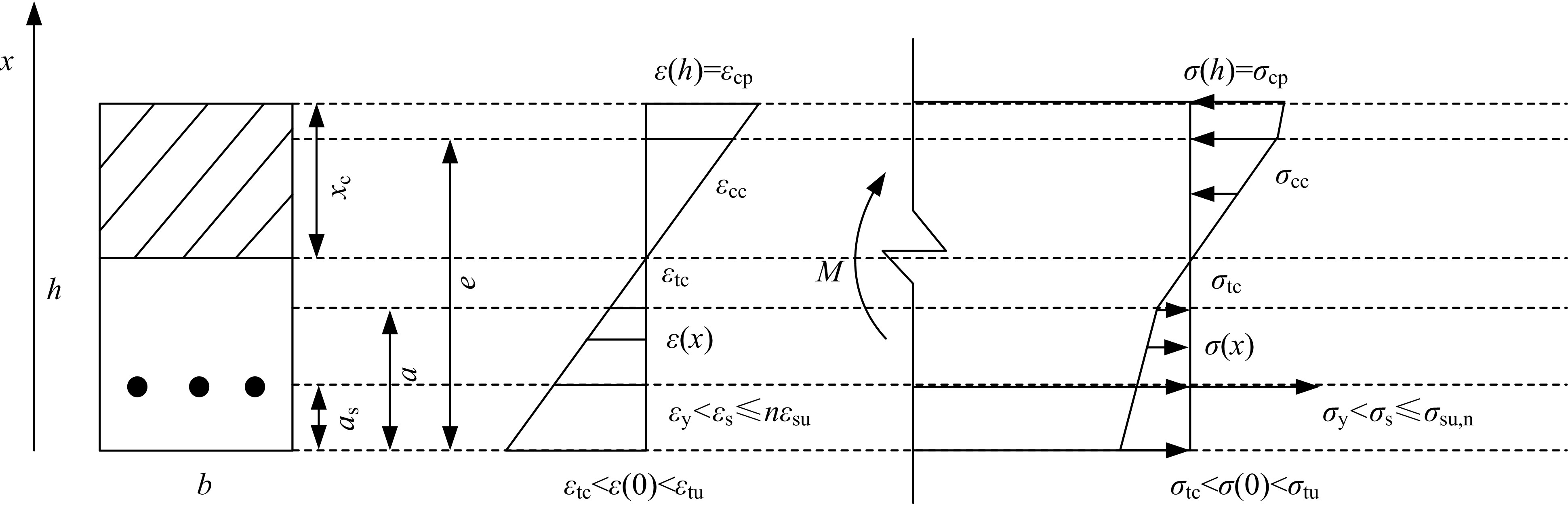
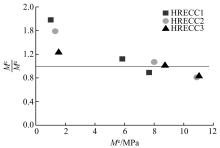
以工程用水泥基复合材料及超高强钢筋的应力-应变本构关系为基础，根据平均应变的平截面假定和梁受拉区ECC不退出工作等假定，建立超高强钢筋ECC梁正截面受弯计算理论，得到了开裂弯矩、屈服弯矩、极限弯矩、界限配筋率和最小配筋率的计算方法。最后，通过文献中的试验结果验证了本文计算理论的合理性。

关键词: 工程力学, 工程用水泥基复合材料, 超高强钢筋, 计算理论, 正截面承载力, 受弯构件

Abstract:

A new type of reinforced Engineered Cementitious Composites (ECC) beam was proposed with ultra high strength bars, named ultra high strength rebar reinforced ECC beam (UHSRRE). The tensile bearing capacity of ultra high strength reinforcement was expected to be efficiently utilized until the requirements of serviceability limit state were not met in UHSRRE. Theoretical analysis on the flexural behavior of UHSRRE was conducted. Three kinds of moments at different phases, including cracking moment, yielding moment and ultimate moment, were estimated with three fundamental hypotheses to calculate the flexural capacity. These hypotheses were the constitutive relationships of ECC and ultra high strength rebar, plane section assumption of mean strain, and the tensile stress of ECC in the tensile area of beam. In addition, the requirements of boundary and minimum reinforcement ratio were defined. These theoretical models were verified by the experimental results .

Key words: engineering mechanics, engineered cementitious composites（ECC）, ultra high strength rebar, calculation theory, bearing capacity of cross section, flexural member

中图分类号: 

  • TU375.1

图1

ECC单轴受拉应力?应变理论曲线"

图2

ECC单轴受压应力?应变理论曲线"

图3

超高强钢筋应力?应变理论曲线"

图4

第Ⅰ阶段末梁截面应力、应变分布"

图5

第Ⅱ阶段末（受压区处于弹性状态）梁截面应力、应变分布"

图6

第Ⅱ阶段末（受压区进入弹塑性状态）梁截面应力、应变分布"

图7

第Ⅲ阶段末梁截面应力、应变分布"

表1

UHSRRE受弯理论值与试验值"

编号 开裂弯矩/（kN·m） M c r c M c r e 屈服弯矩/（kN·m） M y c M y e 极限弯矩/（kN·m） M u c M u e
M c r c M c r e M y c M y e M u c M u e
HRECC1 1.80 1.01 1.78 6.58 5.85 1.12 6.81 7.66 0.89
HRECC2 2.08 1.31 1.59 8.59 8.00 1.07 8.83 10.87 0.81
HRECC3 1.89 1.54 1.23 8.82 8.73 1.01 9.19 11.03 0.83

图8

理论值与试验值对比结果"

表2

理论分析结果"

编号

最小配筋率

/%

实际配筋率

/%

x c b

/mm

界限配筋率

/%

 受压区ECC应力（应变）状态

破坏

类型
第Ⅱ阶段末 第Ⅲ阶段末
HREEC1

0

0

0

 0.56

85.02

85.02

3.88

3.88

 弹性

压区边缘ECC

达单轴受压峰

值应变

延性破坏

延性破坏

延性破坏
HRECC2 0.84 弹塑性
HRECC3 1.12 73.52 3.79 弹塑性
1 Li V C , Leung C K Y . Steady⁃state and multiple cracking of short random fiber composites[J]. Journal of Engineering Mechanics, 1992, 118(11): 2246⁃2264.
2 Li V C . From micromechanics to structural engineering——the design of cementitious composites for civil engineering applications [J]. Journal of Structural Mechanics and Earthquake Engineering,1993,10(2):37⁃48.
3 Said S H , Razak H A . The effect of synthetic polyethylene fiber on the strain hardening behavior of engineered cementitious composite (ECC)[J]. Materials and Design, 2015, 86: 447⁃457.
4 Dehghani A , Nateghi⁃Alahi F , Fischer G . Engineered cementitious composites for strengthening masonry infilled reinforced concrete frames [J]. Engineering Structures, 2015, 105: 197⁃208.
5 Khan M I , Abbass W . Flexural behavior of high⁃strength concrete beams reinforced with a strain hardening cement⁃based composite layer [J]. Construction and Building Materials, 2016, 125: 927⁃935.
6 乔治, 潘钻峰, 梁坚凝, 等 . ECC/RC组合梁受弯性能试验研究与分析[J]. 东南大学学报: 自然科学版, 2017, 47(4): 724⁃731.
Qiao Zhi , Pan Zuan⁃feng , Liang Jian⁃ning , et al . Experimental study and analysis of flexural behavior of ECC/RC composite beams[J]. Journal of Southeast University(Natural Science Edition),2017,47(4): 724⁃731.
7 Yuan Fang , Pan Jin⁃long , Dong Luo⁃ting , et al . Mechanical behaviors of steel reinforced ECC or ECC/concrete composite beams under reversed cyclic loading[J]. Journal of Materials in Civil Engineering, 2014, 26(8): 86⁃88.
8 Xu Shi⁃lang , Hou Li⁃jun , Zhang Xiu⁃fang . Flexural and shear behaviors of reinforced ultrahigh toughness cementitious composite beams without web reinforcement under concentrated load[J]. Engineering Structures, 2012, 39(10): 176⁃186.
9 Li Qing⁃hua , Xu Shi⁃lang . A design concept with the use of RUHTCC beam to improve crack control and durability of concrete structures[J]. Materials and Structures, 2011, 44(6): 1151⁃1177.
10 Meng Dan , Huang Ting , Zhang Y X , et al . Mechanical behaviour of a polyvinyl alcohol fibre reinforced engineered cementitious composite (PVA⁃ECC) using local ingredients [J]. Construction & Building Materials, 2017, 141:259⁃270.
11 Paegle I , Fischer G . Phenomenological interpretation of the shear behavior of reinforced engineered cementitious composite beams [J]. Cement and Concrete Composites, 2016, 73: 213⁃225.
12 Maalej M , Li V C . Flexural/tensile strength ratio in engineered cementitious composites[J]. Journal of Materials in Civil Engineering, 1994, 6(4): 513⁃528.
13 Zhou Jia⁃jia , Pan Jin⁃long , Leung C K Y . Mechanical behavior of fiber⁃reinforced engineered cementitious composites in uniaxial compression[J]. Journal of Materials in Civil Engineering, 2014, 27(1): 04014111.
14 Mohammed B S , Nuruddin M F , Aswin M , et al . Structural behavior of reinforced self⁃compacted engineered cementitious composite beams[J]. Advances in Materials Science and Engineering,2016,225:1⁃12.
15 Noushini A , Samali B , Vessalas K . Ductility and damping characteristics of PVA⁃FRC beam elements[J]. Advances in Structural Engineering, 2015, 18(11): 1763⁃1788.
16 Cai Jing⁃ming , Pan Jin⁃long , Yuan Fang . Experimental and numerical study on flexural behaviors of steel reinforced engineered cementitious composite beams[J].Journal of Southeast University, 2014, 30(3): 330⁃335.
17 Yuan Fang , Pan Jing⁃long , Wu Yu⁃fei . Numerical study on flexural behaviors of steel reinforced engineered cementitious composite (ECC) and ECC/concrete composite beams[J]. Science China Technological Sciences, 2014, 57(3): 637⁃645.
18 薛会青, 邓宗才 . HRECC梁弯曲性能的试验研究与理论分析[J]. 土木工程学报, 2013, 46(4): 10⁃17.
Xue Hui⁃qing , Deng Zong⁃cai . Experimental and theoretical studies on bending performance of HRECC beams[J]. China Civil Engineering Journal, 2013, 46(4): 10⁃17.
[1] 尼颖升,孙启鑫,马晔,徐栋,刘超. 基于空间网格分析的多箱室波形钢腹板组合梁腹板剪力分配[J]. 吉林大学学报(工学版), 2018, 48(6): 1735-1746.
[2] 闫亚宾, 王晓媛, 万强. 纳米尺度界面低周疲劳破坏行为[J]. 吉林大学学报(工学版), 2017, 47(4): 1201-1206.
[3] 陈江义, 刘保元. 纤维断裂损伤对复合材料板中导波频散特性的影响[J]. 吉林大学学报(工学版), 2017, 47(1): 180-184.
[4] 孟广伟, 冯昕宇, 周立明, 李锋. 基于降维算法的结构可靠性分析[J]. 吉林大学学报(工学版), 2017, 47(1): 174-179.
[5] 杨慧艳, 何晓聪, 周森. 压印接头强度的有限元模型及理论计算方法[J]. 吉林大学学报(工学版), 2015, 45(3): 864-871.
[6] 张庆, 王磊. 基于微分方程组的多排桩内力分析[J]. 吉林大学学报(工学版), 2014, 44(5): 1327-1333.
[7] 赵世佳, 徐涛, 陈炜, 谭丽辉. 接近亏损系统模态灵敏度分析的有效算法[J]. 吉林大学学报(工学版), 2013, 43(增刊1): 497-499.
[8] 徐涛, 赵世佳, 张炜, 谭丽辉, 吕岗, 李恒. N重亏损系统摄动的原点移位组合近似方法[J]. 吉林大学学报(工学版), 2012, 42(增刊1): 147-150.
[9] 闫光, 范舟, 李钟海, 程小全, 刘克格, 左春柽. 复合材料加口盖柱壳的设计与分析[J]. , 2012, (06): 1437-1441.
[10] 李春良1,2,王国强1,刘福寿3,赵凯军4. 盾构管片结构的力学行为分析[J]. 吉林大学学报(工学版), 2011, 41(6): 1669-1674.
[11] 张道明1,郭学东2,赵志蒙3. 钢筋混凝土梁弯曲损伤分析的摄动法[J]. 吉林大学学报(工学版), 2011, 41(05): 1358-1363.
[12] 陈耕野, 王彦召, 姚战卫. 平行弦钢桁架应力与感应电动势随荷载的变化[J]. 吉林大学学报(工学版), 2010, 40(增刊): 222-0227.
[13] 贾超, 纪圣振, 张峰. 青岛海湾大桥混凝土墩的时变可靠度[J]. 吉林大学学报(工学版), 2010, 40(06): 1543-1549.
[14] 陆念力,张宏生. 计及纵横变形效应的几何非线性三次样条梁单元[J]. 吉林大学学报(工学版), 2010, 40(03): 745-0751.
[15] 朴香兰,王国强,张占强,郝万军. 水平转弯颗粒流的离散元模拟[J]. 吉林大学学报(工学版), 2010, 40(01): 98-0102.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
版权所有 © 《吉林大学学报(工学版)》编辑部
地址：长春市人民大街5988号　电话：+86-431-85095297　传真：+86-431-85094074　E-mail: xbgxb@jlu.edu.cn
本系统由北京玛格泰克科技发展有限公司设计开发