吉林大学学报(工学版) ›› 2020, Vol. 50 ›› Issue (2): 703-710.doi: 10.13229/j.cnki.jdxbgxb20181221
• 通信与控制工程 • 上一篇
基于托普利兹矩阵集重构的相干信源波达方向估计
- 1.哈尔滨工业大学 电子与信息工程学院,哈尔滨 150001
2.北方民族大学 电信学院,银川 750021
3.哈尔滨工业大学(威海) 信息工程研究所,山东 威海 264209
Toeplitz matrices reconstruction based DOA estimation for coherent signals
Wei ZHANG1,2( ),Yong HAN3,Ming JIN3(
),Yong HAN3,Ming JIN3( ),Xiao-lin QIAO3
),Xiao-lin QIAO3
- 1.School of Electronics and Information Engineering, Harbin Institute of Technology, Harbin 150001
2.School of Electrical & Information Engineering, North Minzu University, Yinchuan 750021, China
3.School of Information Engineering, Harbin Institute of Technology at Weihai, Weihai 264209, China
摘要:
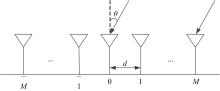
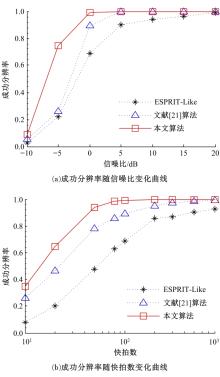
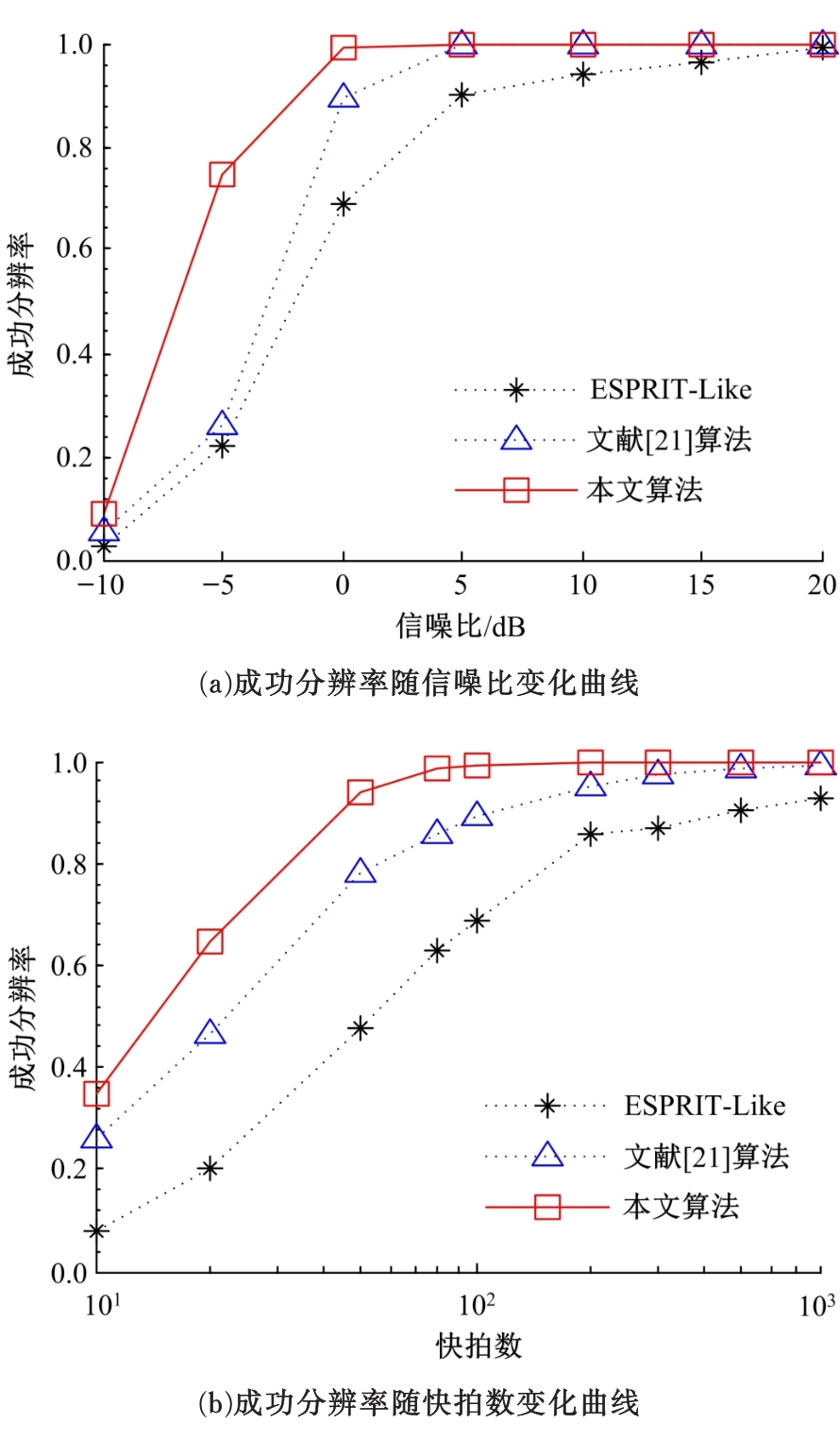
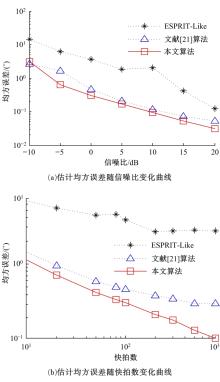
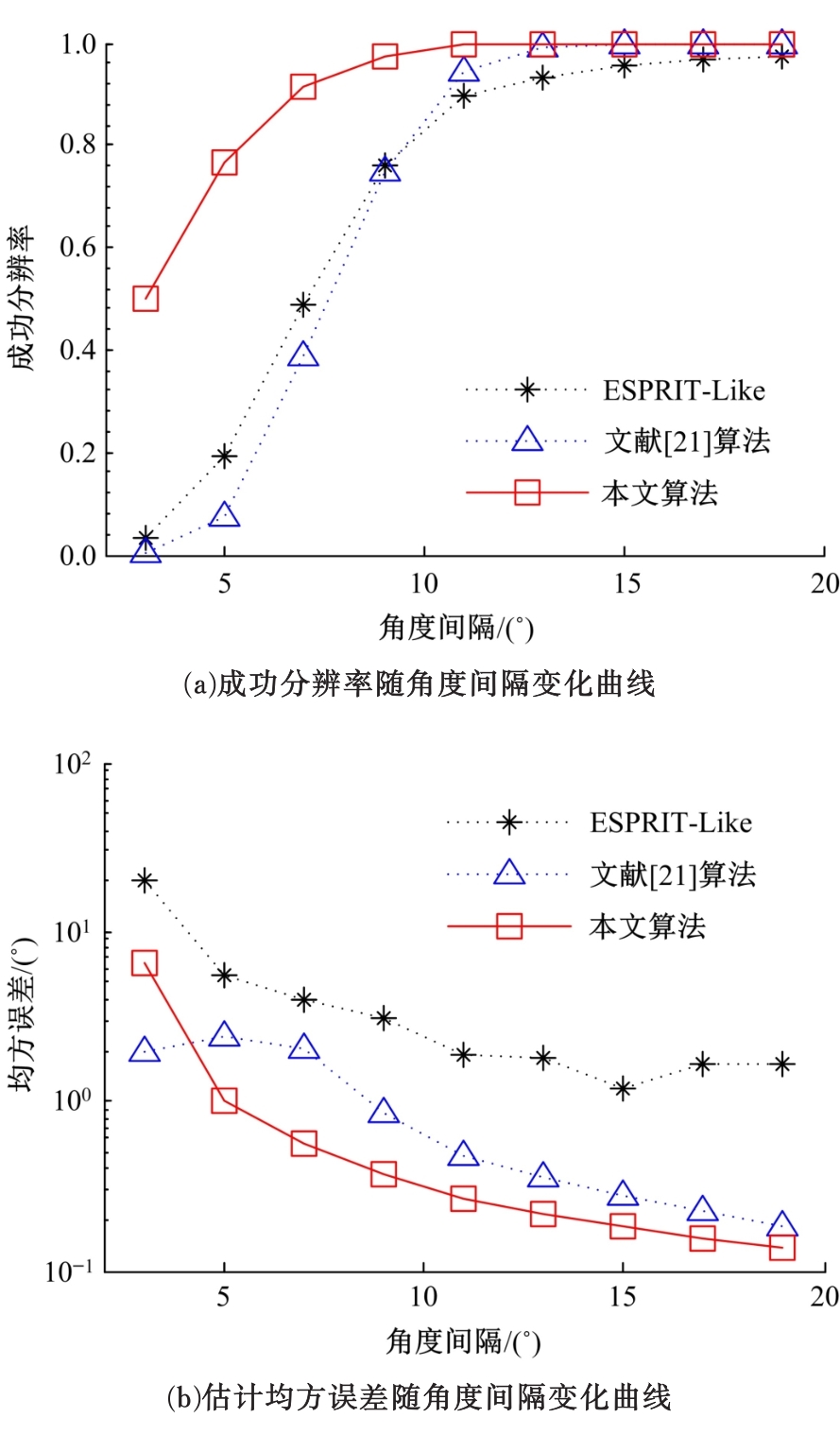
针对常规相干信源波达方向估计托普利兹矩阵重构算法仅利用部分阵列接收数据的互相关或协方差矩阵进行重构,信息利用不完整且部分算法需去噪声处理等问题,提出一种改进托普利兹矩阵重构算法。利用阵元接收数据矢量构造包含阵元完整相关矩阵信息的托普利兹矩阵集,通过Hermitian转置矩阵修正及正反向平滑运算得到满秩矩阵,并结合运算量低的ESPRIT算法实现相干信号角度估计,同时避免去噪声处理。计算机仿真结果验证了算法的有效性。
中图分类号:
- TN911.7
| 1 | Huang H, Liao B, Guo X, et al. DOA estimation of rectilinear signals with a partly calibrated uniform linear array[J]. Signal Processing, 2018, 147: 203-207. |
| 2 | Krim H, Viberg M. Two decades of array signal processing research: the parametric approach[J]. IEEE Signal Processing Magazine, 1996, 13(4): 67-94. |
| 3 | Shi J, Hu G, Zhang X, et al. Generalized co-prime MIMO radar for DOA estimation with enhanced degrees of freedom[J]. IEEE Sensors Journal, 2018, 18(3): 1203-1212. |
| 4 | Zhao W, Li G, Zheng C, et al. Capon cepstrum weighted l2, 1 minimization for wideband DOA estimation with sonar arrays[C]∥OCEANS 2016-Shanghai. IEEE, Shanghai, China, 2016: 1-4. |
| 5 | Shafin R, Liu L, Zhang J, et al. DOA estimation and capacity analysis for 3-D millimeter wave massive-MIMO/FD-MIMO OFDM systems[J]. IEEE Transactions on Wireless Communications, 2016, 15(10): 6963-6978. |
| 6 | Schmidt R O. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276-280. |
| 7 | Roy R, Kailath T. ESPRIT-estimation of signal parameters via rotational invariance techniques[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(7): 984-995. |
| 8 | Shan T J, Wax M, Kailath T. On spatial smoothing for direction-of-arrival estimation of coherent signals[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1985, 33(4): 806-811. |
| 9 | Pillai S U, Kwon B H. Forward/backward spatial smoothing techniques for coherent signal identification[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(1): 8-15. |
| 10 | 石要武, 陈淼, 单泽涛, 等. 基于特征空间MUSIC算法的相干信号波达方向空间平滑估计[J]. 吉林大学学报: 工学版, 2017, 47(1): 268-273. |
| Shi Yao-wu, Chen Miao, Shan Ze-tao, et al. Spatial smoothing technique for coherent signal DOA estimation based on eigen space MUSIC algorithm[J]. Journal of Jilin University (Engineering and Technology Edition), 2017, 47(1): 268-273. | |
| 11 | 甄佳奇, 司锡才, 王桐, 等. 基于正交直线阵列的二维相干源测向方法[J]. 吉林大学学报: 工学版, 2009, 39(6): 1659-1663. |
| Zhen Jia-qi, Si Xi-cai, Wang Tong, et al. Approach to 2-D DOA estimation for coherent signals based on orthogonal linear array[J]. Journal of Jilin University (Engineering and Technology Edition), 2009, 39(6): 1659-1663. | |
| 12 | Han F M, Zhang X D. An ESPRIT-like algorithm for coherent DOA estimation[J]. IEEE Antennas and Wireless Propagation Letters, 2005, 4(1): 443-446. |
| 13 | 陈辉, 黄本雄, 王永良. 基于互相关矢量重构的解相干算法研究[J]. 系统工程与电子技术, 2008, 30(6): 1005-1008, 1036. |
| Chen Hui, Huang Ben-xiong, Wang Yong-liang. DOA estimation of coherent signals based on cross-correlation vector reconstruction[J]. Systems Engineering and Electronics, 2008, 30(6): 1005-1008, 1036. | |
| 14 | Jabr K A, Kwon H M, Tayem N. Modified UCA-ESPRIT for estimating DOA of coherent signals using one snapshot[C]∥Vehicular Technology Conference, IEEE, 2008: 290-293. |
| 15 | Ren S, Ma X, Yan S, et al. 2-D unitary ESPRIT-like direction-of-arrival(DOA) estimation for coherent signals with a uniform rectangular array[J]. Sensors, 2013, 13(4): 4272-4288. |
| 16 | 司伟建, 吴迪, 韩惠莲. 基于相关Toeplitz预处理的二维测向方法[J]. 中南大学学报: 自然科学版, 2015, 46(8): 2892-2897. |
| Si Wei-jian, Wu Di, Han Hui-lian. 2-D direction finding method based on correlation Toeplitz pretreatment[J]. Journal of Central South University (Science and Technology), 2015, 46(8): 2892-2897. | |
| 17 | 毛维平, 李国林, 谢鑫, 等. 独立源与相干源并存的信源数估计[J]. 系统工程与电子技术, 2014, 36(3): 422-428. |
| Mao Wei-ping, Li Guo-lin, Xie Xin, et al. Source number estimation of coexisting uncorrelated and coherent sources[J]. Systems Engineering and Electronics, 2014, 36(3): 422-428. | |
| 18 | 谢鑫, 李国林, 刘华文. 采用单次快拍数据实现相干信号DOA估计[J]. 电子与信息学报, 2010, 32(3): 604-608. |
| Xie Xin, Li Guo-lin, Liu Hua-wen. DOA estimation of coherent signals using one snapshot[J]. Journal of Electronics & Information Technology, 2010, 32(3): 604-608. | |
| 19 | 王凌, 李国林, 刘坚强, 等. 一种基于数据矩阵重构的相干信源二维测向新方法[J]. 西安电子科技大学学报: 自然科学版, 2013, 40(2): 130-137. |
| Wang Ling, Li Guo-lin, Liu Jian-qiang, et al. New method for estimating 2-D DOA in the coherent source environment based on data matrix reconstruction[J]. Journal of Xidian University (Natural Science), 2013, 40(2): 130-137. | |
| 20 | 蒋柏峰, 吕晓德, 向茂生. 一种基于阵列接收信号重排的单快拍DOA估计方法[J]. 电子与信息学报, 2014, 36(6): 1334-1339. |
| Jiang Bai-feng, Xiao-de Lyu, Xiang Mao-sheng. Single snapshot DOA estimation method based on rearrangement of array receiving signal[J]. Journal of Electronics & Information Technology, 2014, 36(6): 1334-1339. | |
| 21 | Qian C, Huang L, Zeng W J, et al. Direction-of-arrival estimation for coherent signals without knowledge of source number[J]. IEEE Sensors Journal, 2014, 14(9): 3267-3273. |
| [1] | 程艳芬,姚丽娟,袁巧,陈先桥. 水下视频图像清晰化方法[J]. 吉林大学学报(工学版), 2020, 50(2): 668-677. |
| [2] | 于晓辉,张志成,李新波,孙晓东. 基于状态空间模型的指数衰减正弦信号参数估计[J]. 吉林大学学报(工学版), 2019, 49(6): 2083-2088. |
| [3] | 刘富, 权美静, 王柯, 刘云, 康冰, 韩志武, 侯涛. 仿蝎子振源定位机理的位置指纹室内定位方法[J]. 吉林大学学报(工学版), 2019, 49(6): 2076-2082. |
| [4] | 马子骥,卢浩,董艳茹. 双通道单图像超分辨率卷积神经网络[J]. 吉林大学学报(工学版), 2019, 49(6): 2089-2097. |
| [5] | 王洪雁,房云飞,朱圣棋,裴炳南. 非均匀噪声条件下考虑互耦效应的DOA估计方法[J]. 吉林大学学报(工学版), 2019, 49(5): 1706-1714. |
| [6] | 郭继昌,吴洁,郭春乐,朱明辉. 基于残差连接卷积神经网络的图像超分辨率重构[J]. 吉林大学学报(工学版), 2019, 49(5): 1726-1734. |
| [7] | 曹运合,曾丽,王宇. 基于特征空间的子阵级自适应和差波束测角方法[J]. 吉林大学学报(工学版), 2019, 49(5): 1735-1744. |
| [8] | 卢洋,王世刚,赵文婷,赵岩. 基于离散Shearlet类别可分性测度的人脸表情识别方法[J]. 吉林大学学报(工学版), 2019, 49(5): 1715-1725. |
| [9] | 董超,刘晶红,徐芳,王仁浩. 光学遥感图像舰船目标快速检测方法[J]. 吉林大学学报(工学版), 2019, 49(4): 1369-1376. |
| [10] | 王柯俨,胡妍,王怀,李云松. 结合天空分割和超像素级暗通道的图像去雾算法[J]. 吉林大学学报(工学版), 2019, 49(4): 1377-1384. |
| [11] | 托乎提努尔,张海龙,王杰,王娜,冶鑫晨,王万琼. 基于图形处理器的高速中值滤波算法[J]. 吉林大学学报(工学版), 2019, 49(3): 979-985. |
| [12] | 付银娟,李勇,徐丽琴,张昆辉. NLFM⁃Costas射频隐身雷达信号设计及分析[J]. 吉林大学学报(工学版), 2019, 49(3): 994-999. |
| [13] | 苏寒松,代志涛,刘高华,张倩芳. 结合吸收Markov链和流行排序的显著性区域检测[J]. 吉林大学学报(工学版), 2018, 48(6): 1887-1894. |
| [14] | 应欢,刘松华,唐博文,韩丽芳,周亮. 基于自适应释放策略的低开销确定性重放方法[J]. 吉林大学学报(工学版), 2018, 48(6): 1917-1924. |
| [15] | 陆智俊,钟超,吴敬玉. 星载合成孔径雷达图像小特征的准确分割方法[J]. 吉林大学学报(工学版), 2018, 48(6): 1925-1930. |
|
||