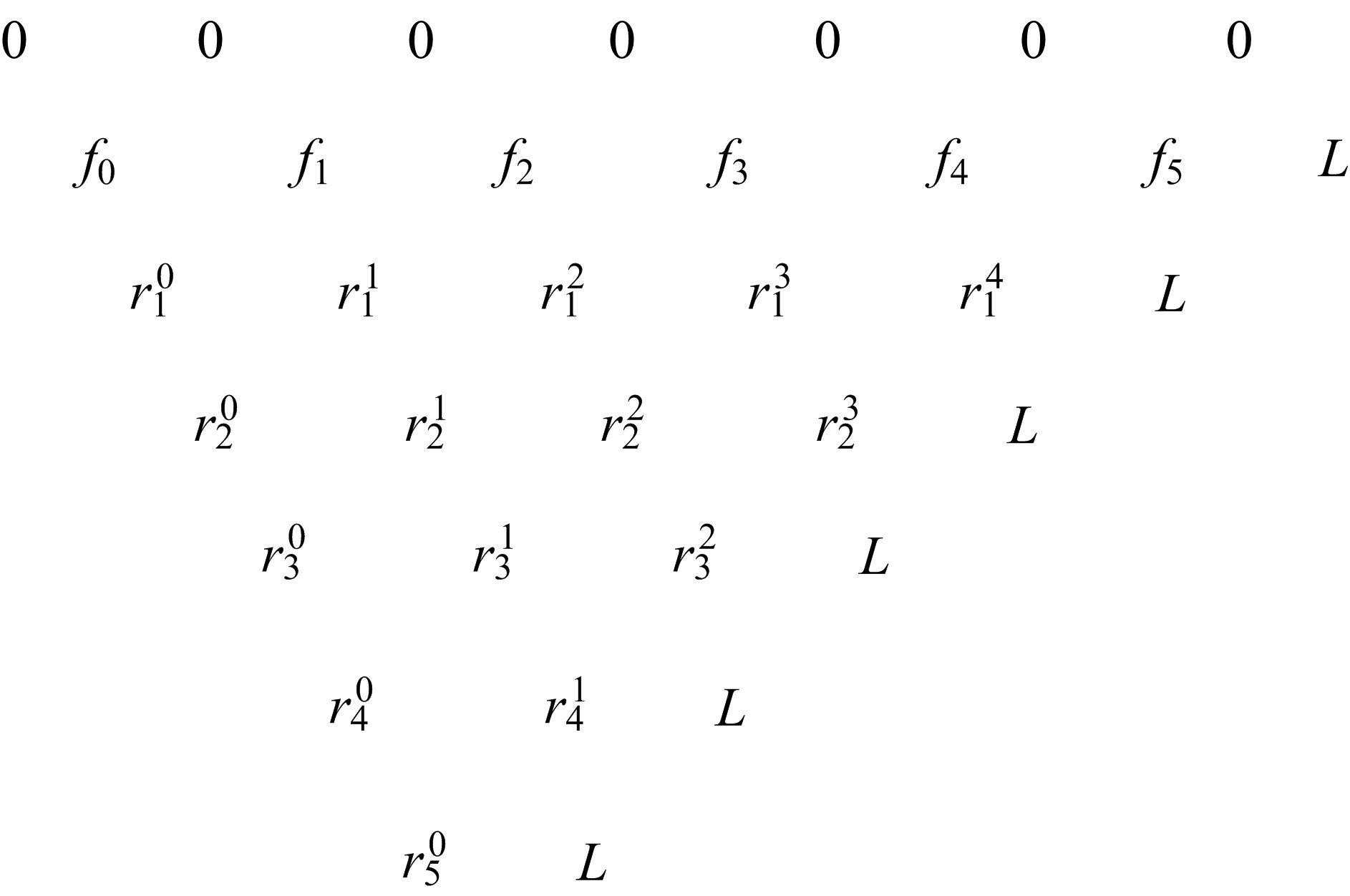吉林大学学报(工学版) ›› 2021, Vol. 51 ›› Issue (2): 472-477.doi: 10.13229/j.cnki.jdxbgxb20191183

• 车辆工程·机械工程 • 上一篇    

结构静态位移一阶和二阶灵敏度近似计算方法

麻凯1(),李邦辉1,杨坤2(),刘巧伶1   

  1. 1.吉林大学 机械与航空航天工程学院，长春 130022
    2.空军航空大学 航空基础学院，长春 130022
  • 收稿日期:2019-12-24 出版日期:2021-03-01 发布日期:2021-02-09
  • 通讯作者: 杨坤 E-mail:makai@jlu.edu.cn;Yangkuncust@163.com
  • 作者简介:麻凯（1978-），男，副教授，博士.研究方向：结构重分析，结构优化.E-mail:makai@jlu.edu.cn
  • 基金资助:
    国家自然科学基金项目(51675216)

First and second⁃order sensitivity method of structure static displacement

Kai MA1(),Bang-hui LI1,Kun YANG2(),Qiao-ling LIU1   

  1. 1.College of Mechanical and Aerospace Engineering，Jilin University，Changchun 130022，China
    2.Basic Education College of Aviation University of Air Force，Changchun 130022，China
  • Received:2019-12-24 Online:2021-03-01 Published:2021-02-09
  • Contact: Kun YANG E-mail:makai@jlu.edu.cn;Yangkuncust@163.com

RICH HTML

 5   

PDF (PC)

88

摘要：

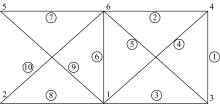
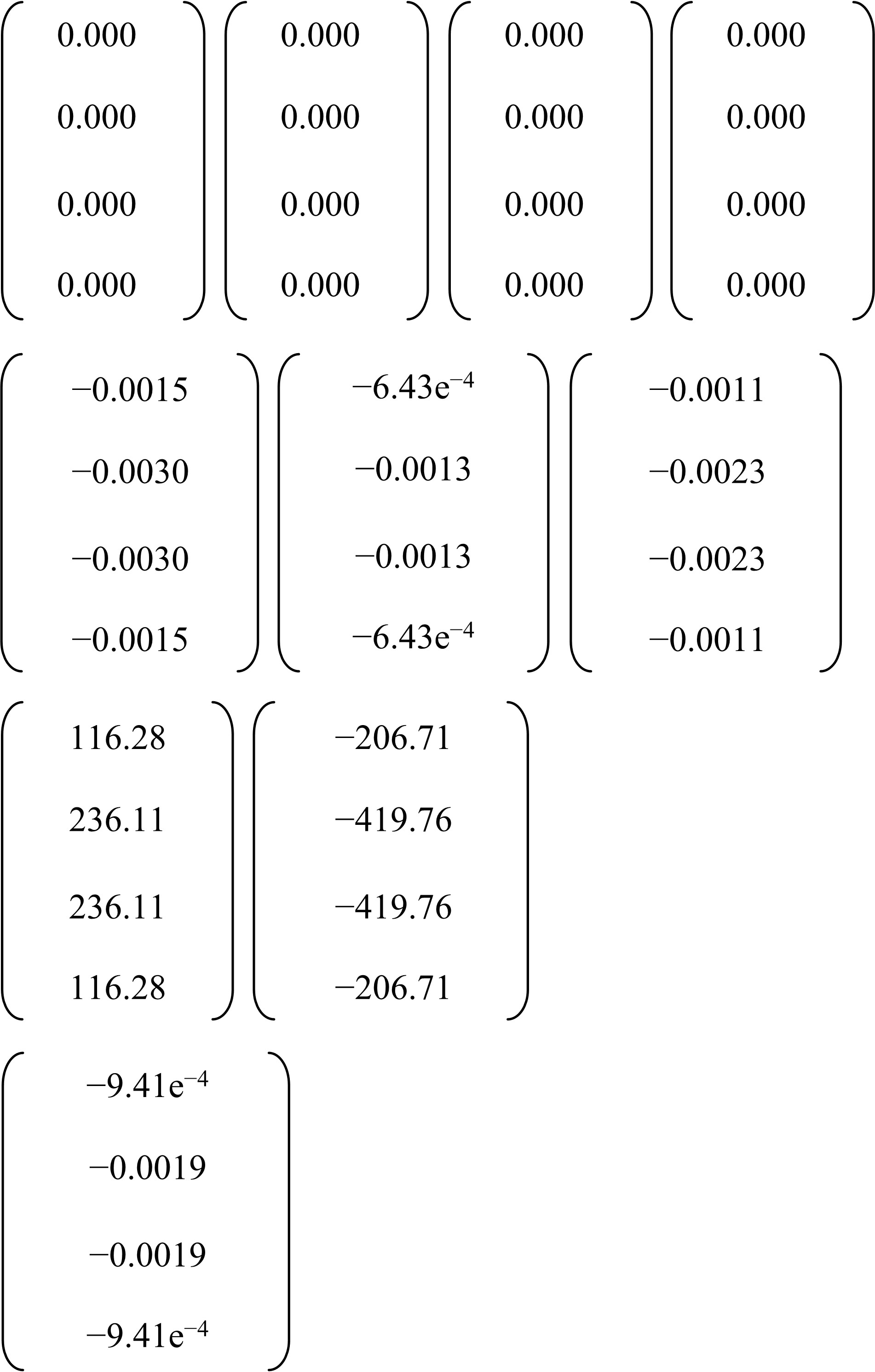
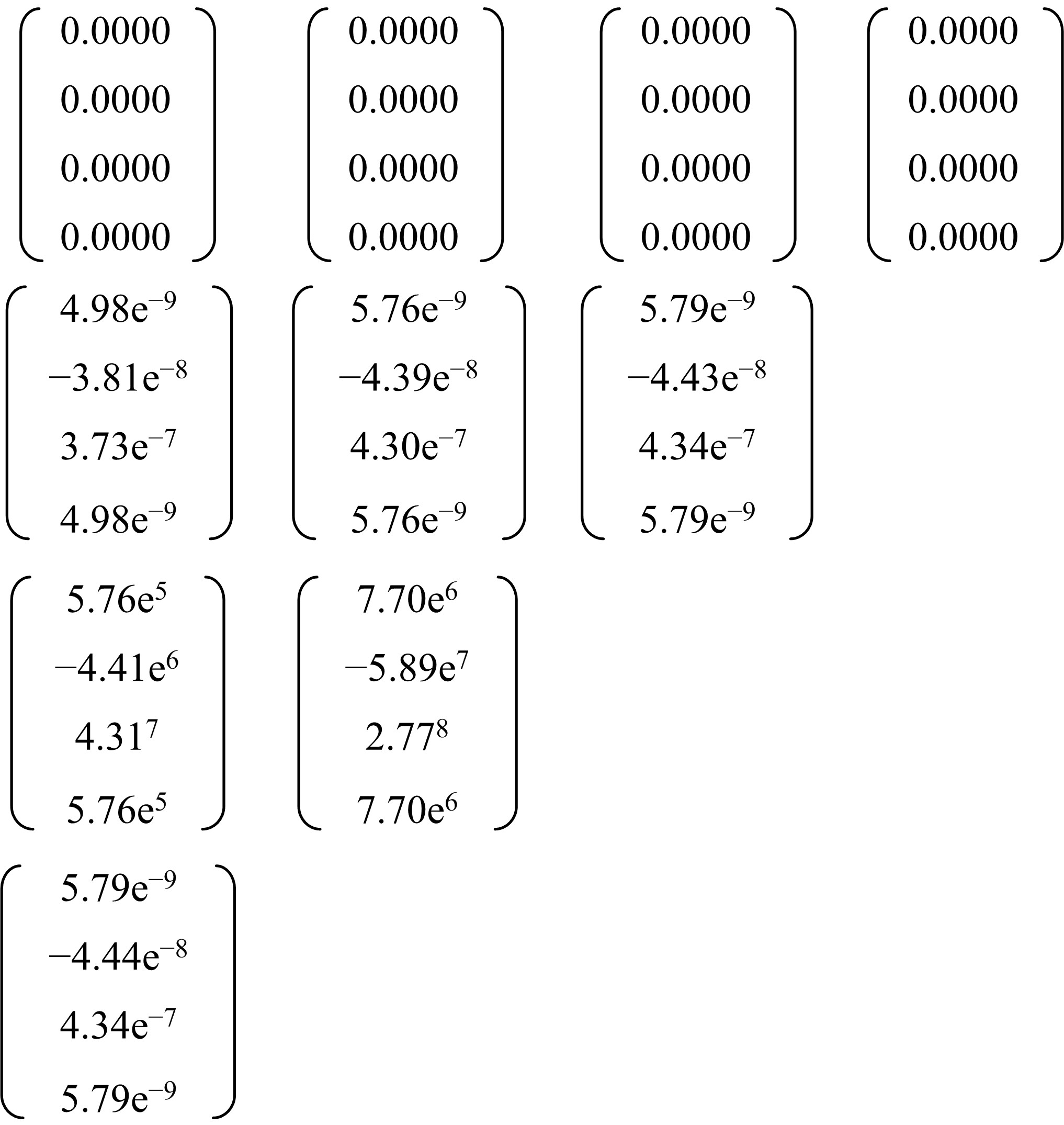
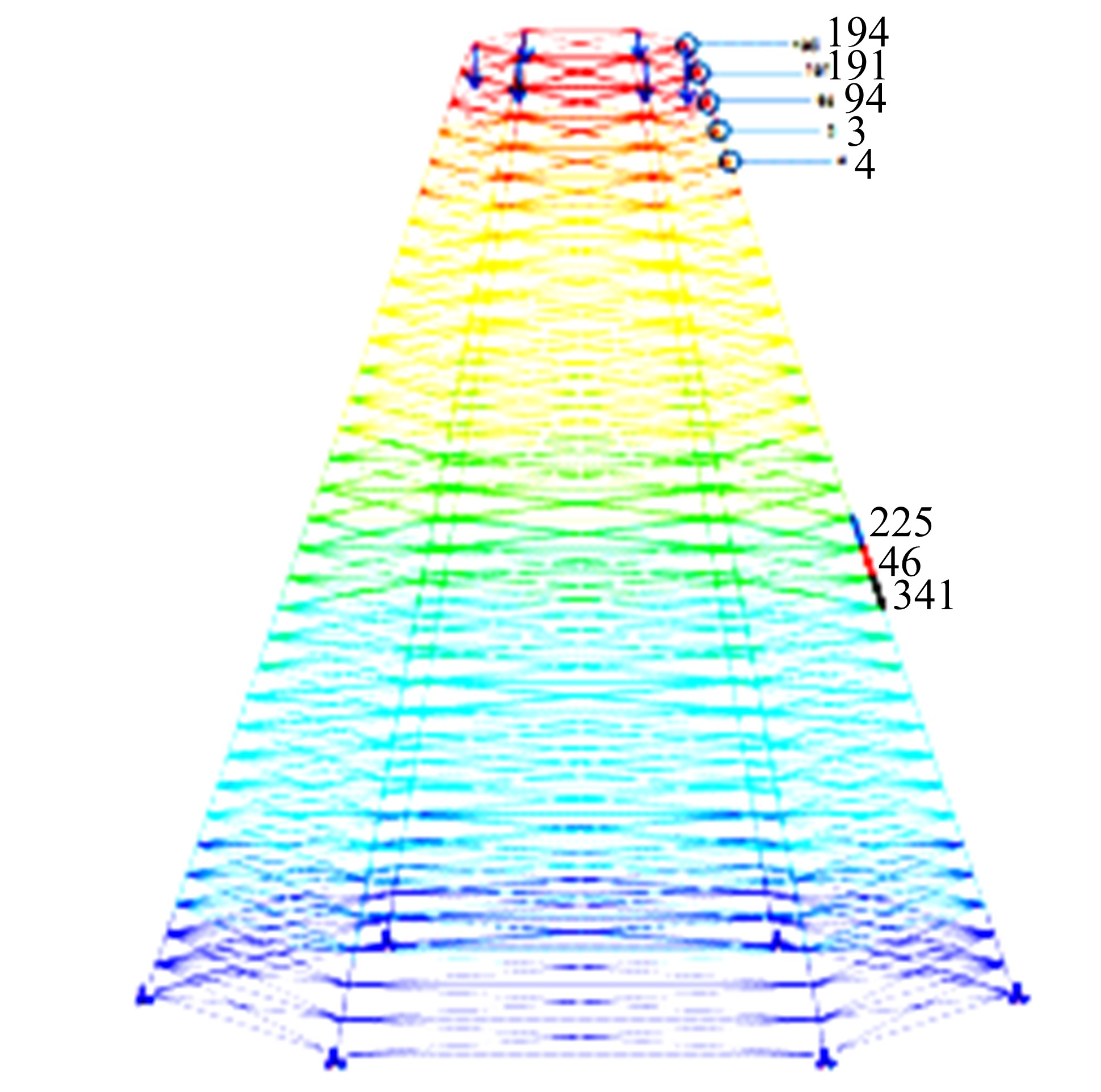
提出一种基于Epsilon算法和改进的纽曼级数的结构静态位移的一阶和二阶灵敏度近似计算方法。本文将Epsilon算法与改进的纽曼级数法结合形成新的静态位移快速近似计算方法，并进一步推导出了静态位移一阶灵敏度快速近似计算方法；然后利用差分方法与一阶灵敏度方法结合进一步推导出静态位移二阶灵敏度近似计算方法。桁架模型和梁模型灵敏度计算结果表明了两种灵敏度方法的工程应用价值。

关键词: 改进的纽曼级数, Epsilon算法, 灵敏度分析, 结构重分析

Abstract:

Based on Epsilon algorithm and improved Neumann series， an approximate method for calculating the first and second order sensitivity of structural static displacement is proposed. First， the Epsilon algorithm is combined with the improved Neumann series to form a new fast approximate calculation method of static displacement， and a fast approximate calculation method of the first-order sensitivity of static displacement is derived. Then， the second-order sensitivity approximate calculation method of static displacement is further derived by combining the difference method with the first-order sensitivity method. The sensitivity calculation results of truss model and beam model show the engineering application value of the two sensitivity methods.

Key words: improved Newman series, Epsilon algorithm, sensitivity analysis, structural reanalysis

中图分类号: 

  • O342

图1

Epsilon算法计算流程表"

图2

忽略奇数行的计算结果"

图3

平面桁架结构"

图4

一阶灵敏度计算结果"

图5

二阶灵敏度计算结果"

表1

一阶位移灵敏度（算例1）"

节点编号 及位移方向精确解近似解误差/%
1-x-1.5E-05-1.50E-050.00E+00
1-y-5.739E-05-5.74E-05-0.005 74
2-x07.74E-507.74E-48
2-y05.04E-365.04E-34
3-x0.000 114 7750.000 114 7770.011 478
3-y0.000 554 1930.000 554 1940.055 419
4-x-0.001 123 375-0.001 123 378-0.112 34
4-y0.000 683 9620.000 683 9610.068 396
5-x01.11E-481.11E-46
5-y0-5.04E-36-5E-34
6-x-1.5E-05-1.50E-05-0.001 5
6-y5.739E-055.74E-050.005 74

表2

二阶位移灵敏度（算例1）"

节点编号 及位移方向精确解近似解误差/%
1-x5.812 5E-095.79E-09-0.310 2
1-y2.218 12E-082.22E-080.011 0
2-x0-2.37E-530
2-y-1.946 9E-39-1.95E-390.003 4
3-x-4.434 4E-08-4.44E-080.053 3
3-y-2.141 9E-07-2.14E-070.014 44
4-x4.341 88E-074.34E-070.012 97
4-y-2.643 5E-07-2.64E-070.012 94
5-x0-6.60E-510
5-y1.946 88E-391.95E-390.003 37
6-x5.812 5E-095.79E-09-0.310 3
6-y-2.218 1E-08-2.22E-080.011 0

图6

梁截面半径为5 mm的六边形塔结构"

图7

一阶灵敏度计算结果"

表3

一阶位移灵敏度（算例2）"

节点编号及位移方向精确解近似解误差/%
190-x0.065 30.065 278 871-0.032
191-x0.061 50.061 475 388-0.04
94-x0.057 70.057 671 711-0.049
3-x0.053 90.053 897 051-0.005 5
4-x0.050 20.050 211 74-0.023 4

表4

二阶位移灵敏度（算例2）"

节点编号及位移方向精确解近似解误差/%
190-x-0.026 35-0.026 5-0.502 8
191-x-0.024 8-0.024 90.563
94-x-0.023 3-0.023 40.415
3-x-0.021 8-0.021 90.300 7
4-x-0.020 3-0.020 40.348 3

图8

二阶灵敏度计算结果"

1 Arora J. Servey of structural reanalysis techniques[J]. Journal of the Structural Division American Society of Civil Engineers, 1976, 102(4): 783-802.
2 Kirsch U, Rubinstein M F. Structural reanalysis by iteration[J]. Computers and Structures, 1972, 2(4): 497-510.
3 Wang H, Li E, Li G. A parallel reanalysis method based on approximate inverse matrix for complex engineering problems[J]. Journal of Mechanical Design, 2013, 135(8): 081001.
4 王琥, 种浩, 高国强, 等. 重分析方法研究进展及展望[J]. 工程力学, 2017, 34(5): 1-16.
Wang Hu, Chong Hao, Gao Guo-qiang, et al. Review of advances and outlook in reanalysis methods[J]. Engineering Mechanics, 2017, 34(5): 1-16.
5 Kirsch U. Implementation of combined approximations instructural optimization[J]. Computers and Structures, 2000, 78(1-3): 449-457.
6 Kirsch U. Approximate vibration reanalysis of structures[J]. AIAA Journal, 2003, 41(3): 504-511.
7 Kirsch U. A unified reanalysis approach for structural analysis design and optimization[J]. Structural and Multidisciplinary Optimization, 2003, 25(2): 67-85.
8 Zuo W, Yu Z, Zhao S, et al. A hybrid fox and Kirsch's reduced basis method for structural static reanalysis[J]. Structural and Multidisciplinary Optimization, 2012, 46(2): 261-272.
9 Sun R, Liu D, Xu T, et al. New adaptive technique of Kirsch method for structural reanalysis[J]. AIAA Journal, 2014, 52(3): 486-495.
10 刘寒冰, 陈塑寰. 结构动特性灵敏度分析的边界元摄动法[J]. 振动与冲击, 1993, 12(3): 25-30.
Liu Han-bing, Chen Su-huan. Boundary element perturbation method for shape design sensitivity analysis of structural dynamic character[J],Journal of Vibration and Shock, 1993, 12(3): 25-30.
11 Kirsch U. Approximate vibration reanalysis of structures[J]. AIAA Journal, 2003, 41(3): 504-511.
12 Lederer C, Altstadt S, Andriamonje S. An efficient reanalysis methodology for probabilistic vibration of largescale structures[J]. Journalof Mechanical Design, 2009, 131(5): 051007.
13 Xu T, Guo G, Zhang H. Vibration reanalysis using frequency-shift combined approximations[J]. Structural and Multi-disciplinary Optimization, 2011, 44(2): 235-246.
14 Gao G, Wang H, Li G. An adaptive time-based global method for dynamic reanalysis[J]. Structural and Multi-disciplinary Optimization, 2013, 48(2): 355-365.
[1] 张泽星, 陈国迎, 宗长富. 基于灵敏度分析的EPS转向性能试验客观评价指标[J]. 吉林大学学报(工学版), 2015, 45(4): 1043-1048.
[2] 柯俊, 陈志勇, 史文库, 施腾, 张一京, 郭福祥. 基于振动控制的客车地板模态分析及结构优化[J]. 吉林大学学报(工学版), 2015, 45(3): 719-725.
[3] 陈书明, 彭登志, 王登峰, 梁杰. 车内低频噪声声固耦合及试验优化设计[J]. 吉林大学学报(工学版), 2014, 44(6): 1550-1556.
[4] 赵世佳, 徐涛, 陈炜, 谭丽辉. 接近亏损系统模态灵敏度分析的有效算法[J]. 吉林大学学报(工学版), 2013, 43(增刊1): 497-499.
[5] 徐涛, 邱冰, 程飞, 金延中, 蒋永洲, 赵世佳. 基于偶数行Epsilon加速的结构拓扑修改重分析算法[J]. 吉林大学学报(工学版), 2011, 41(增刊2): 246-249.
[6] 张英爽1,王国强1,王继新1,侯晓婷1,2,章二平3,黄建兵3. 轮式装载机半轴载荷谱编制及疲劳寿命预测[J]. 吉林大学学报(工学版), 2011, 41(6): 1646-1651.
[7] 高晋, 宋传学. 橡胶衬套刚度对悬架特性的影响[J]. 吉林大学学报(工学版), 2010, 40(02): 324-0329.
[8] 孙睿珩,徐涛,张昊,吕岗,邱冰. 组合近似重分析方法的ANSYS二次开发[J]. 吉林大学学报(工学版), 2009, 39(增刊2): 396-0400.
[9] 高书娜, 邓兆祥, 胡玉梅. 基于声压灵敏度分析的轿车车内低频噪声优化[J]. 吉林大学学报(工学版), 2009, 39(05): 1130-1136.
[10] 王旭，陈永刚，杨印生 . 含有区间数的DEA-DA模型及灵敏度[J]. 吉林大学学报(工学版), 2009, 39(03): 716-0720.
[11] 马梁，陈塑寰，孟广伟 . 区间参数有大变化时的结构特征值分析[J]. 吉林大学学报(工学版), 2009, 39(01): 98-102.
[12] 梁平， 王树范， 王永利，温泳. 轴对称结构拓扑变化重分析的新方法[J]. 吉林大学学报(工学版), 2006, 36(增刊1): 26-0029.
[13] 吴晓明，陈塑寰，黄志东. Epsilon算法在汽车结构设计分析中的应用[J]. 吉林大学学报(工学版), 2006, 36(增刊1): 8-0011.
[14] 吴晓明，陈塑寰. Epsilon算法在结构模态重分析中的应用[J]. 吉林大学学报(工学版), 2006, 36(04): 447-450.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
版权所有 © 《吉林大学学报(工学版)》编辑部
地址：长春市人民大街5988号　电话：+86-431-85095297　传真：+86-431-85094074　E-mail: xbgxb@jlu.edu.cn
本系统由北京玛格泰克科技发展有限公司设计开发