吉林大学学报(工学版) ›› 2023, Vol. 53 ›› Issue (1): 159-169.doi: 10.13229/j.cnki.jdxbgxb20210557

• 交通运输工程·土木工程 • 上一篇    

可液化土阻尼系数对地铁结构地震响应的影响

刘顺1,2(),唐小微1(),栾一晓1   

  1. 1.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116023
    2.中冶京诚工程技术有限公司，北京 100176
  • 收稿日期:2021-06-21 出版日期:2023-01-01 发布日期:2023-07-23
  • 通讯作者: 唐小微 E-mail:ls458047501@163.com;tangxw@dlut.edu.com
  • 作者简介:刘顺（1992-），男，博士研究生. 研究方向：砂土液化，地下工程. E-mail：ls458047501@163.com
  • 基金资助:
    国家重点研究发展计划项目(2021YFB2600703)

Influence of Rayleigh damping coefficient on seismic response of subway structure in liquefiable soil

Shun LIU1,2(),Xiao-wei TANG1(),Yi-xiao LUAN1   

  1. 1.State Key Laboratory of Coastal and Offshore Engineering，Dalian University of Technology，Dalian 116023，China
    2.MCC Capital Engineering & Research Incorporation Limited，Beijing 100176，China
  • Received:2021-06-21 Online:2023-01-01 Published:2023-07-23
  • Contact: Xiao-wei TANG E-mail:ls458047501@163.com;tangxw@dlut.edu.com

RICH HTML

 0   

PDF (PC)

232

摘要：

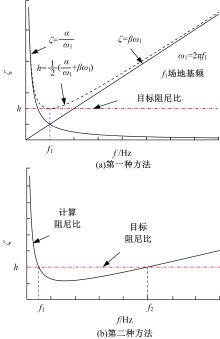
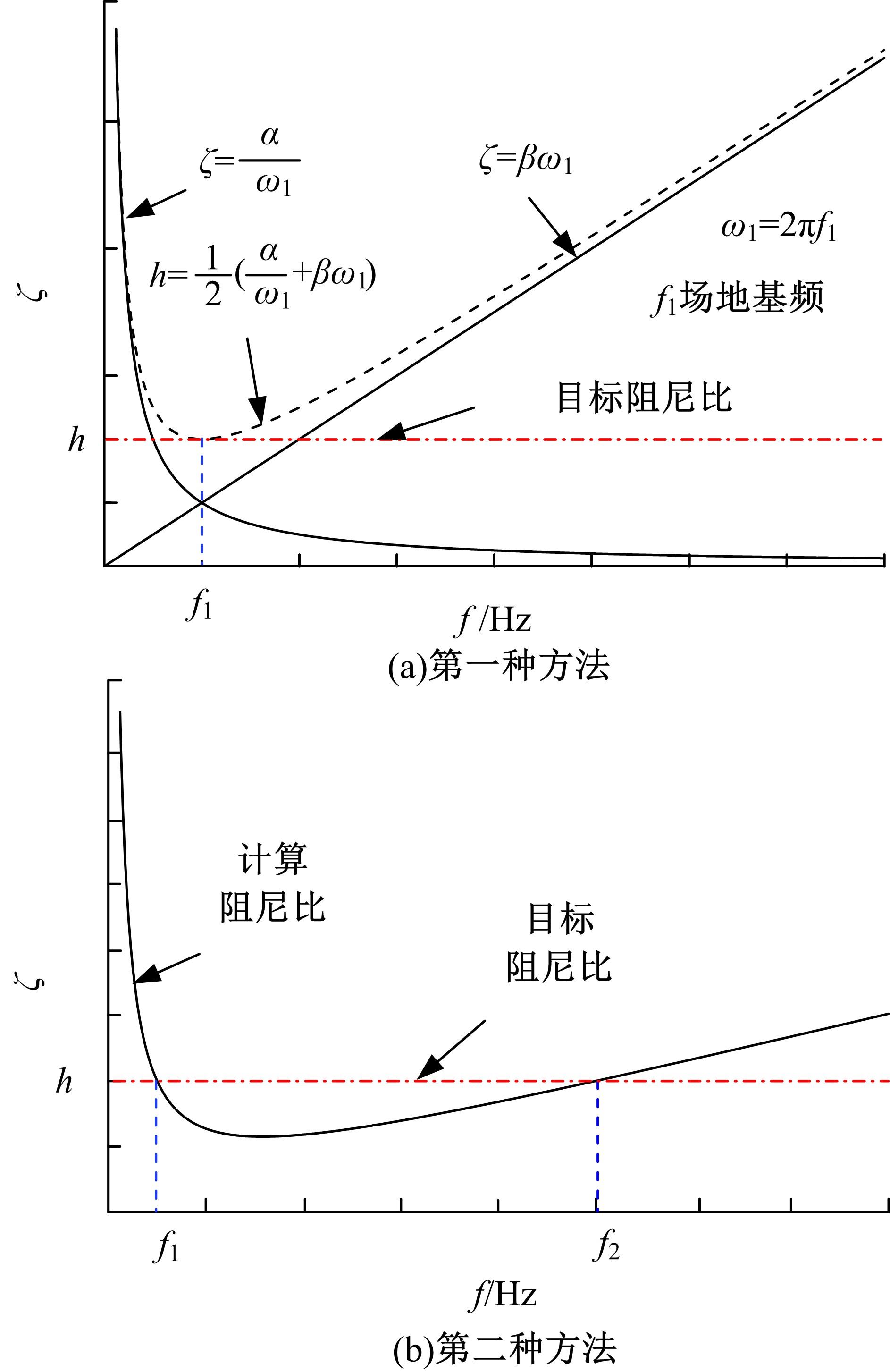
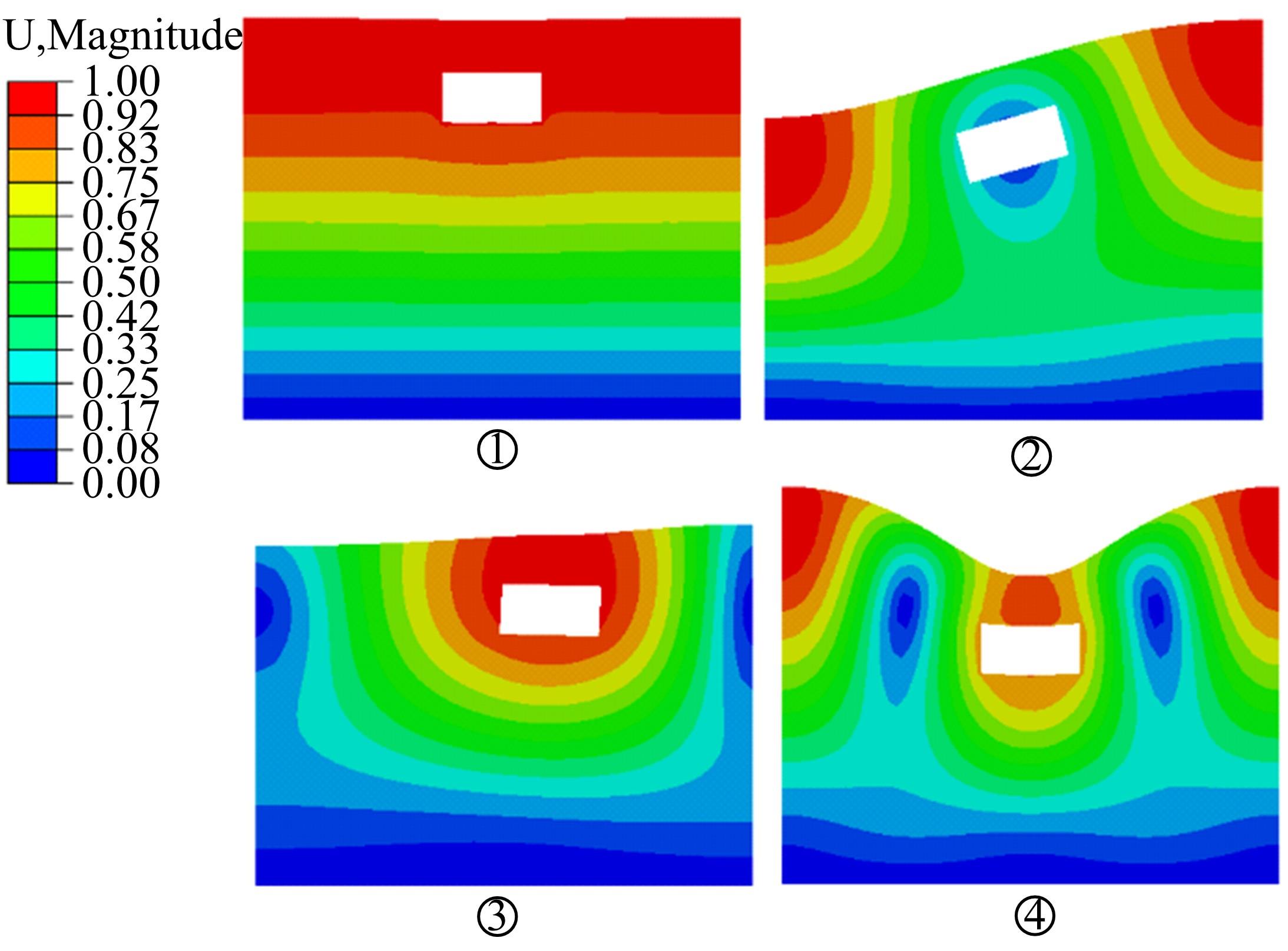
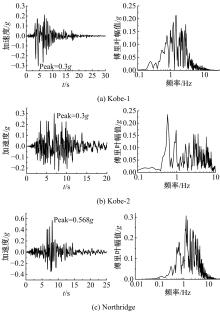
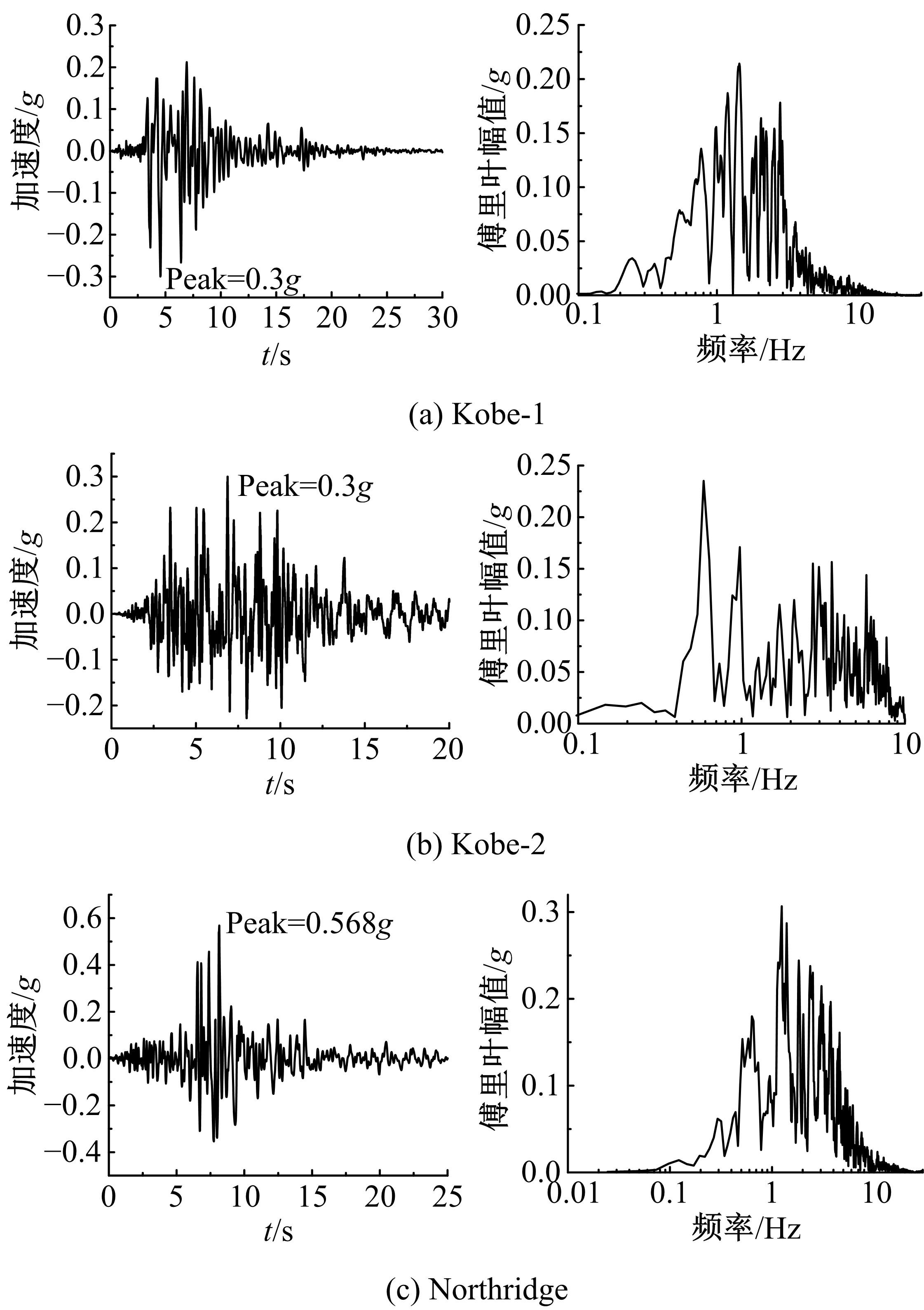
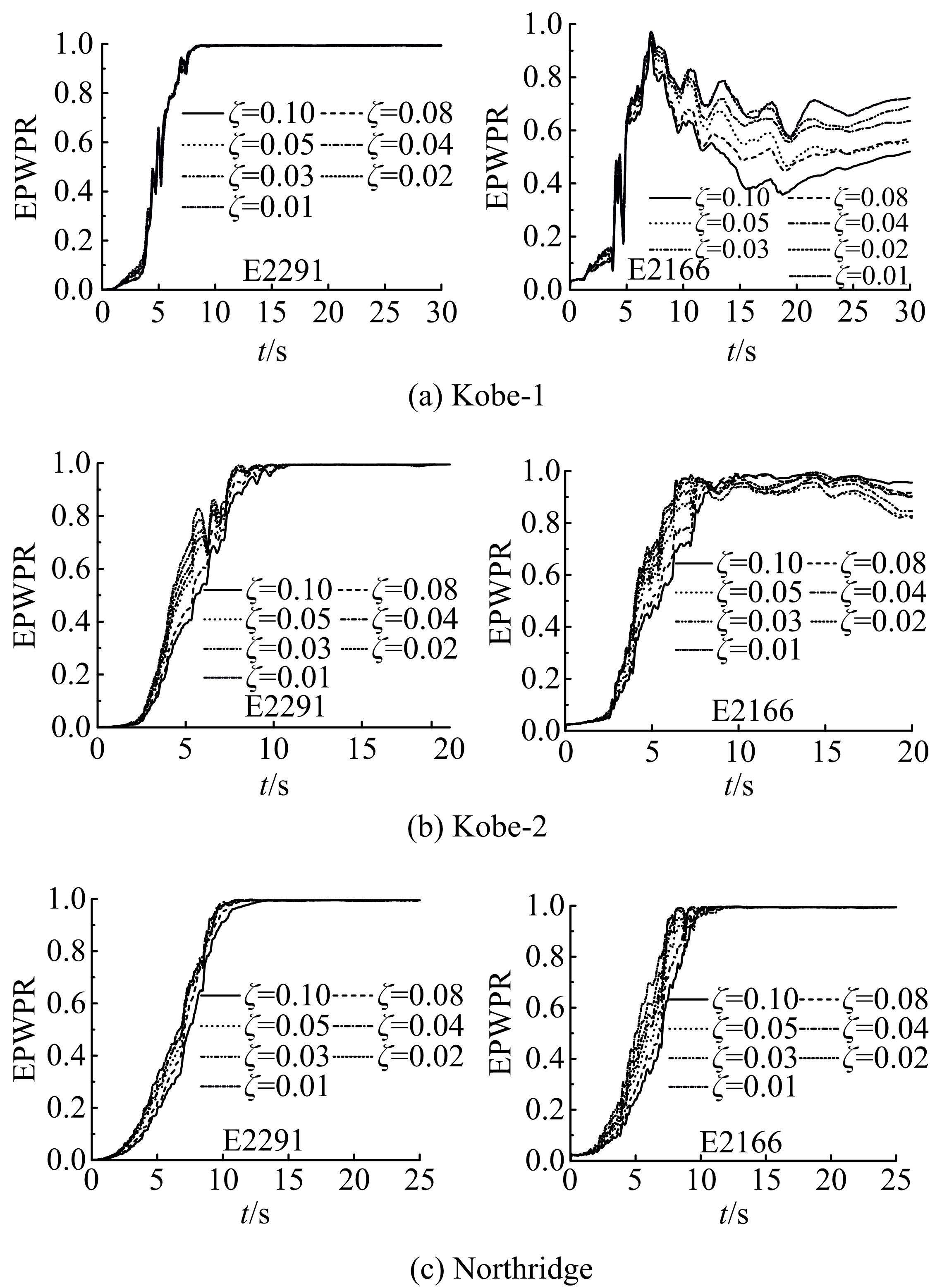
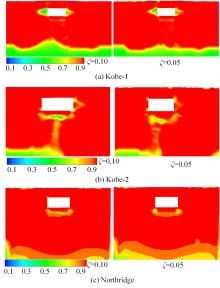
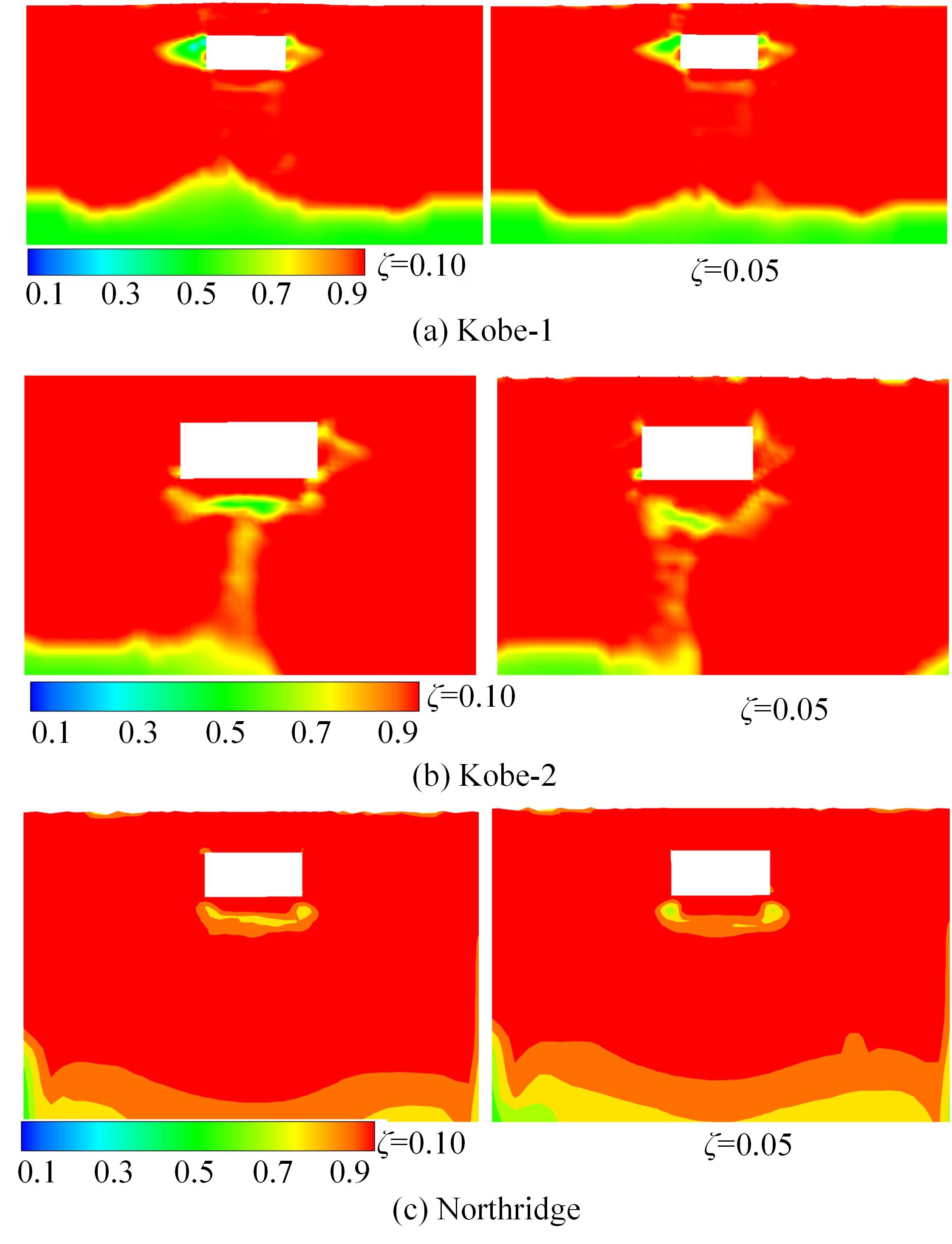
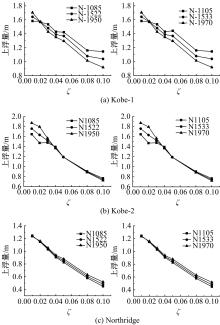
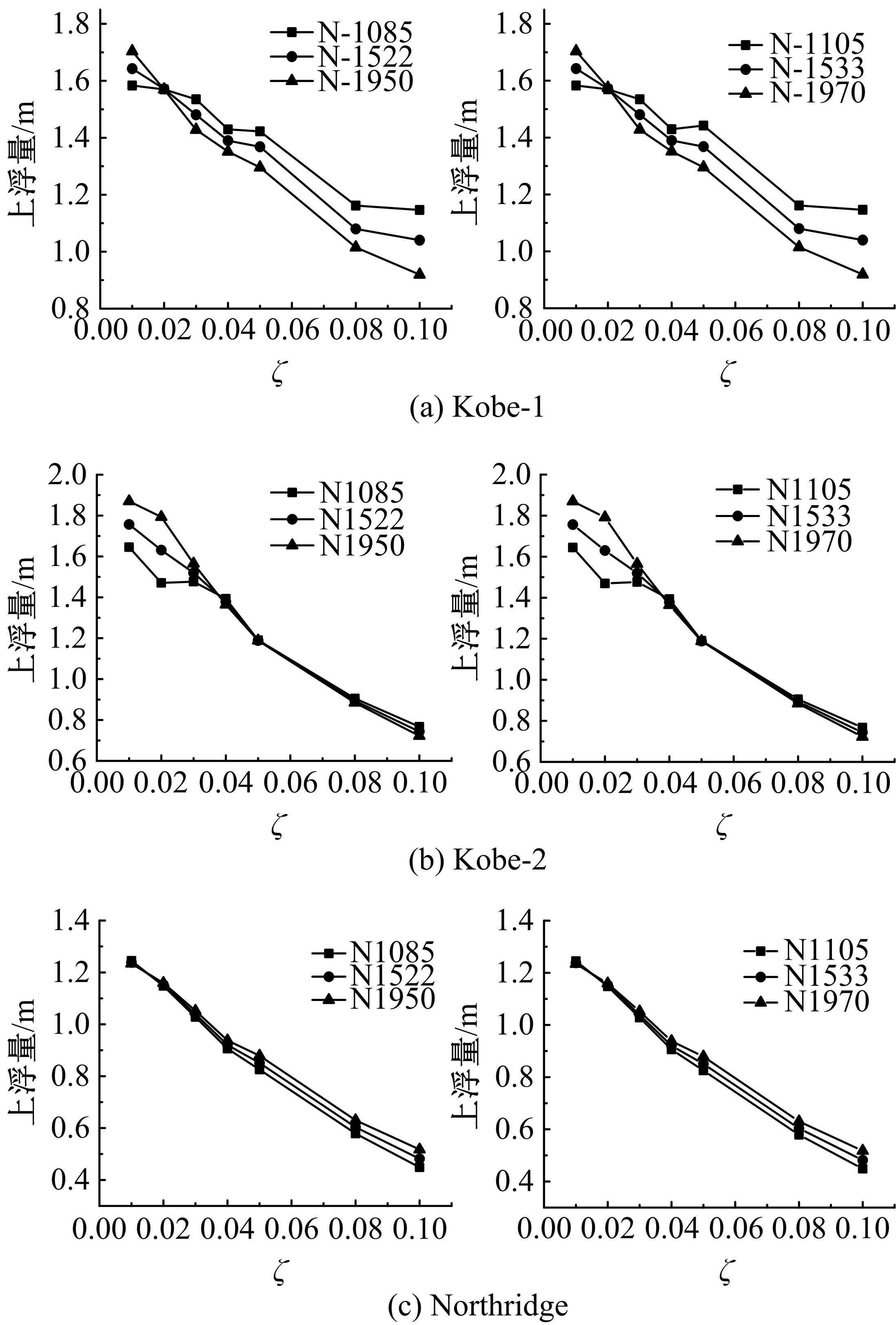
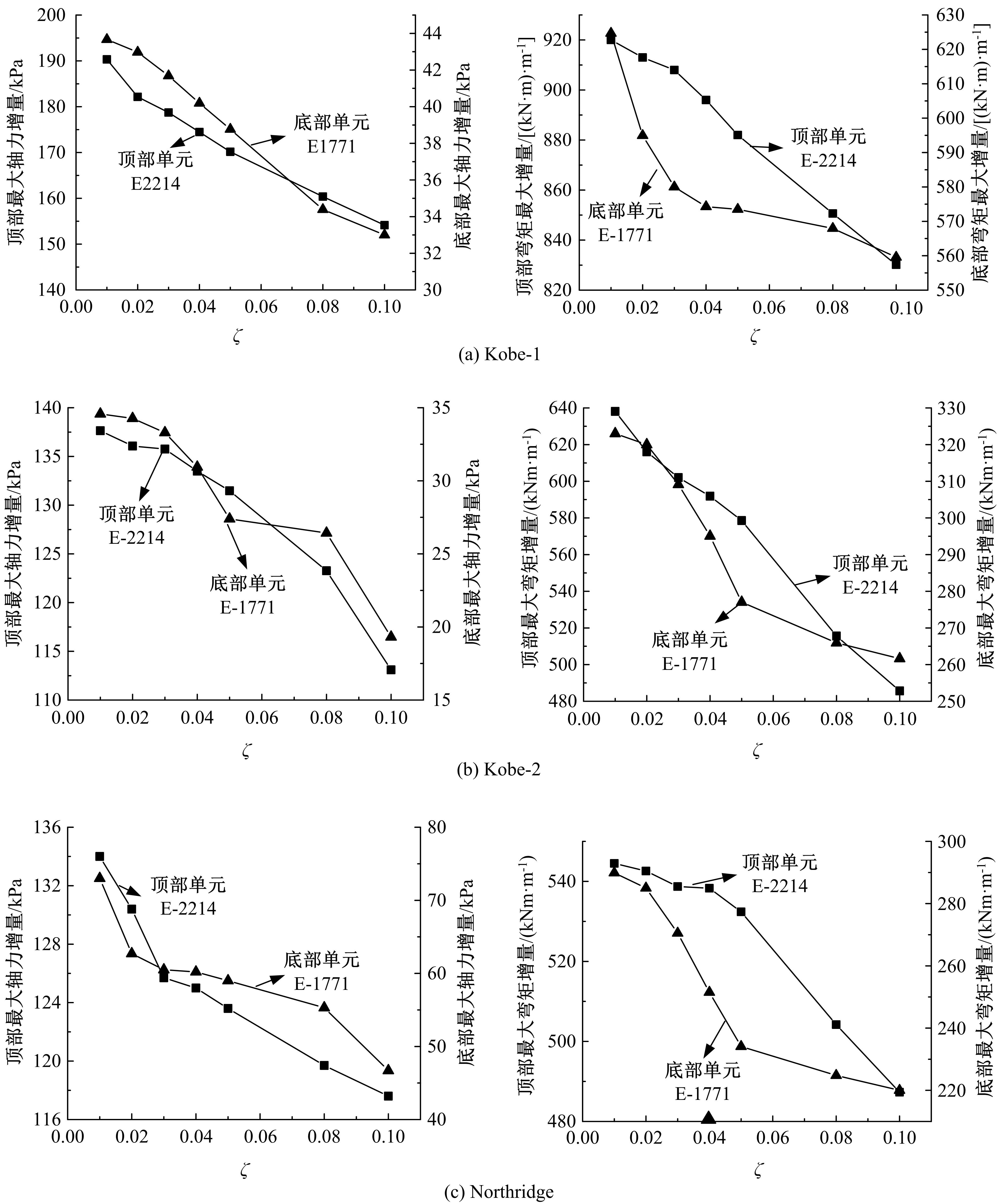
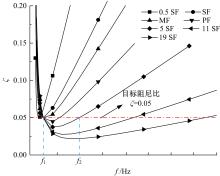
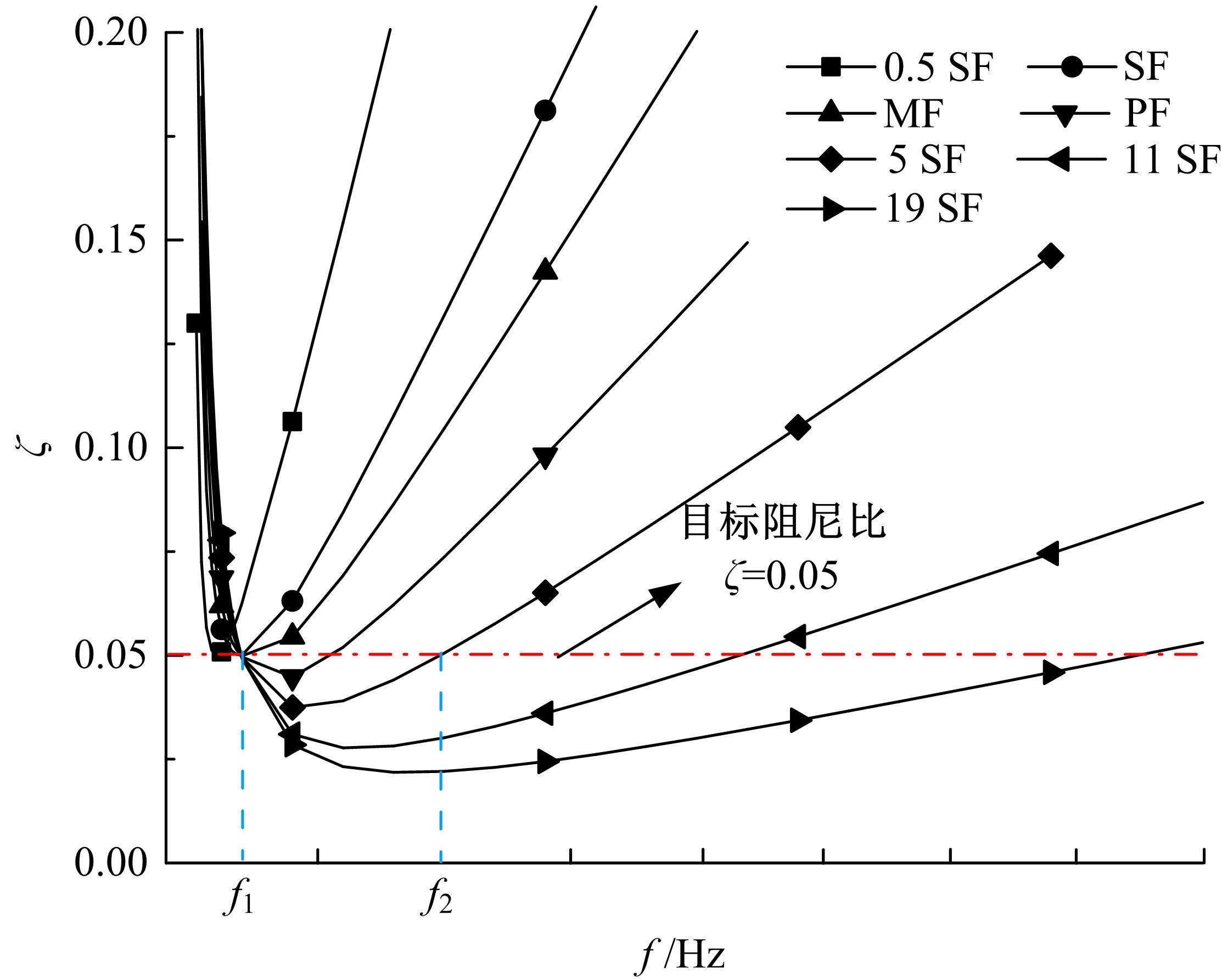
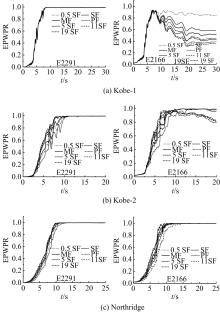
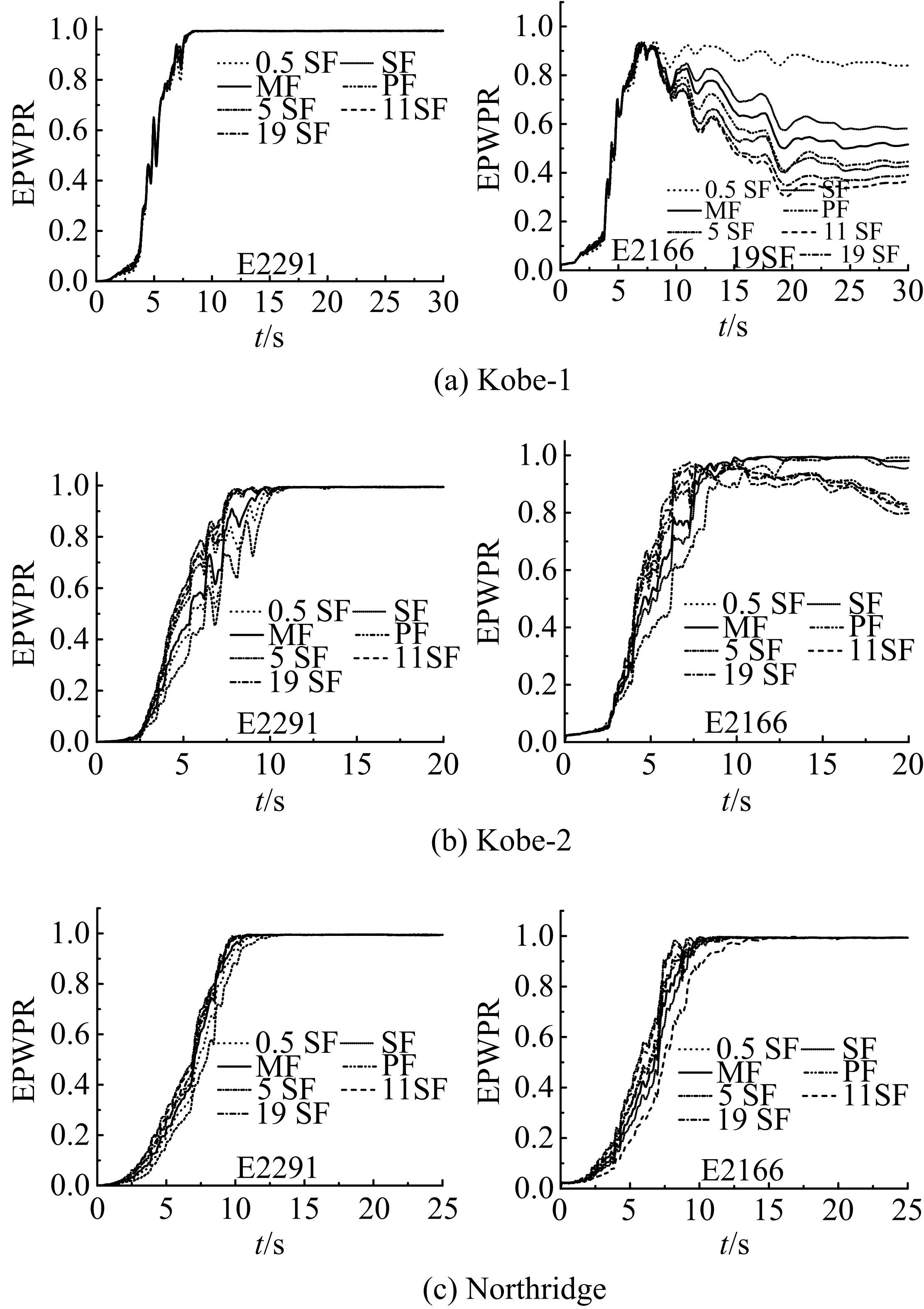
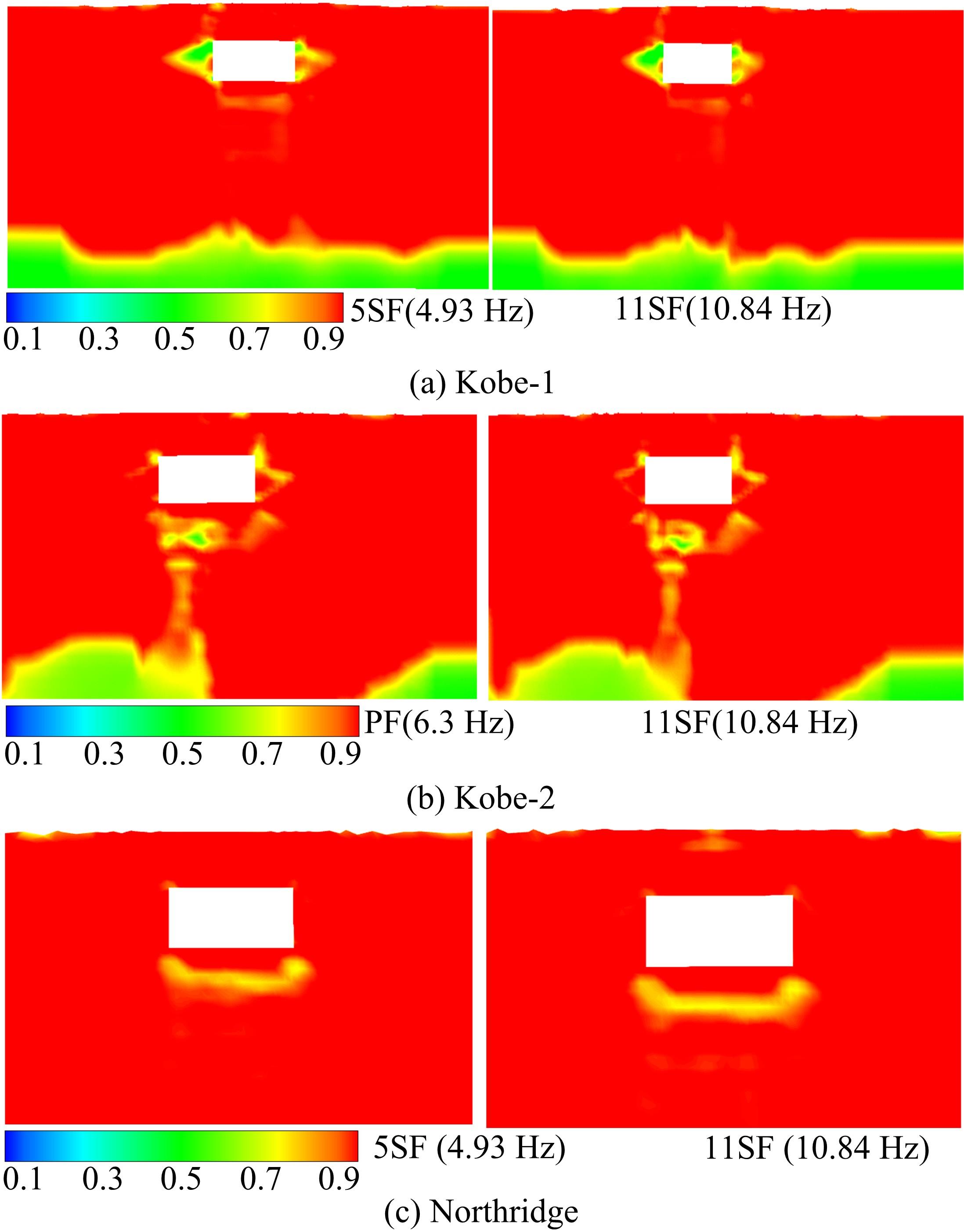
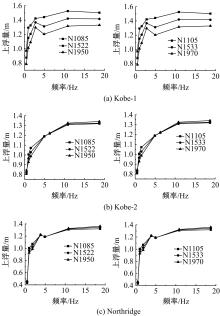
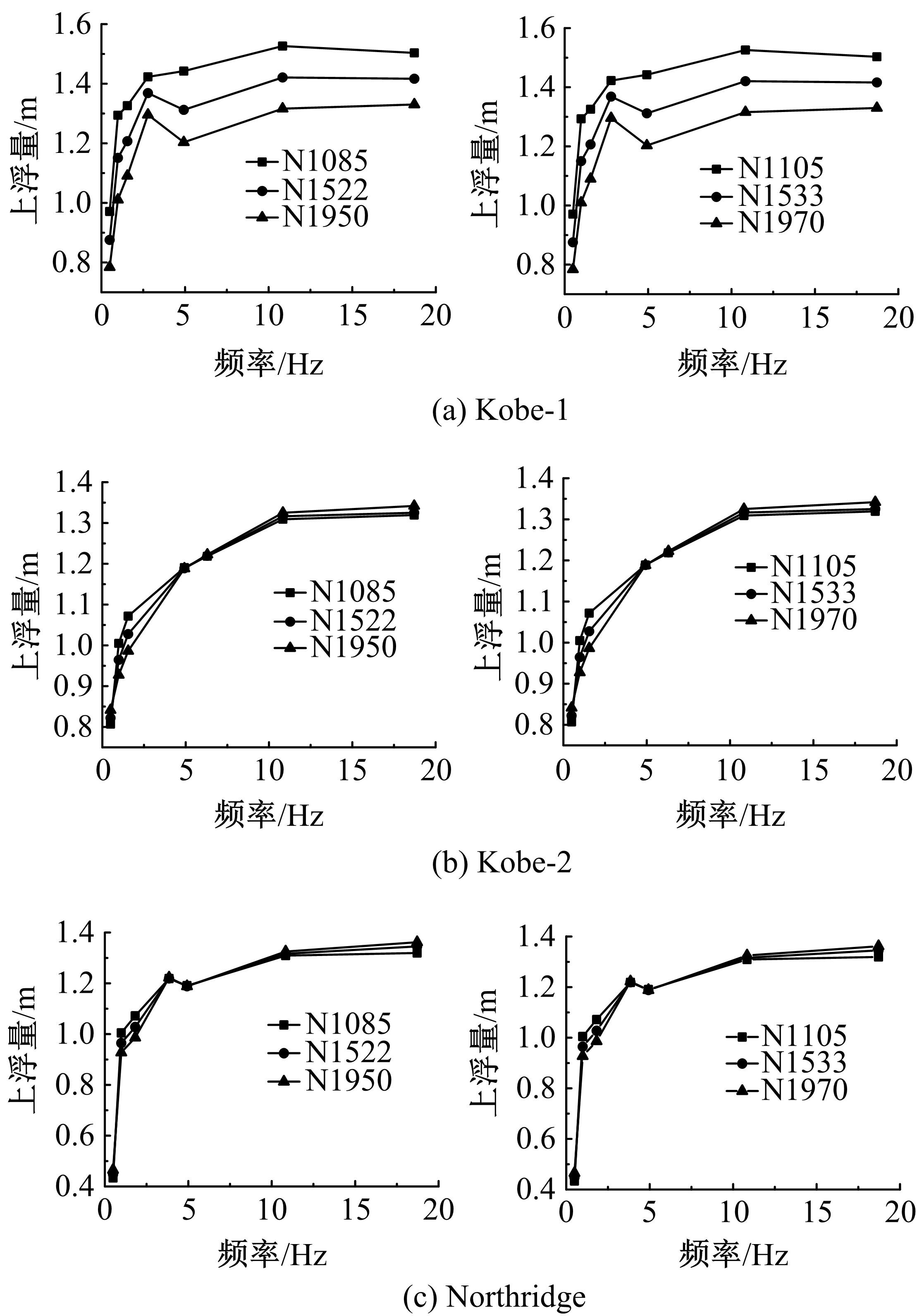
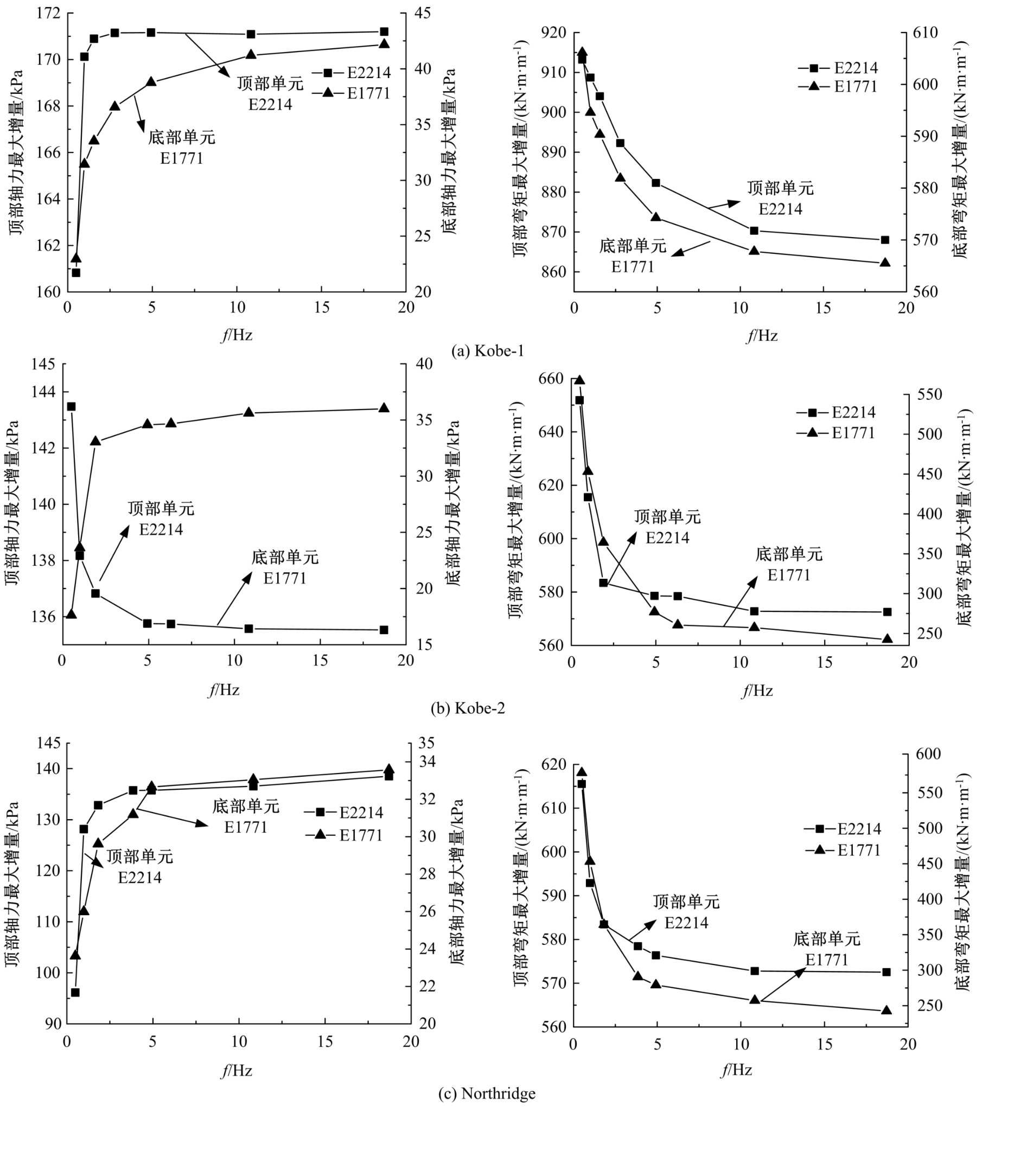
针对Rayleigh阻尼系数的影响因素，分析了目标阻尼比和敏感频率范围选择对地下结构地震下的孔隙水压力、上浮量和结构内力的影响。结果表明，目标阻尼比影响地铁车站的变形形态，且其值越大，土体的超孔隙水压力发展越慢，地铁结构的上浮量和内力增量越小；上限敏感频率的影响存在着阈值，超过阈值，超孔隙水压力、地铁结构上浮量和内力增量的变化基本不受影响。综合分析表明，可液化土中地铁结构动力分析应结合场地和输入震动的特性，充分考虑Rayleigh阻尼的影响因素，合理地引入粘性阻尼。

关键词: 岩土工程, Rayleigh阻尼, 目标阻尼比, 敏感频率, 地铁结构

Abstract:

Considering the influencing factors of the damping coefficient， the influence of the selection of the target damping ratio and the sensitive frequency range on the pore water pressure， the amount of buoyancy and the internal force of the underground structure under seismic loads is analyzed. The results show that the larger the target damping ratio， the slower the increase of the excess pore water pressure of the soil， and the smaller the floating and the internal force increment of subway structure. There is a threshold for the influence of the upper sensitive frequency.When the effect range exceeds the threshold， the excess pore water pressure， the floating and the internal force of the structure are basically unaffected. The analysis shows that the influence factors of Rayleigh damping should be fully considered and the damping coefficient should be determined reasonably in the analysis of liquefaction dynamic of subway structure.

Key words: geotechnical engineering, Rayleigh damping, target damping ratio, sensitive frequency, subway structure

中图分类号: 

  • TU9

图1

计算阻尼比和频率的关系曲线"

图2

地铁车站有限元模型"

图3

模型前四阶模态"

表1

可液化土参数"

变 量数值变 量数值
密度ρ/（kg·m-3）2000破坏应力比Mf1
初始孔隙比e00.8硬化参数B04000
压缩指数λ0.03硬化参数B140
膨胀指数κ0.002剪胀参数D01
渗透系数k/（m·s-1）0.000 03剪胀参数n2
初始剪切比G0/σ'm0343.5塑性参考剪应变γrefp0.003
超固结比OCR1.2弹性参考剪应变γrefe0.035
相变应力比Mm0.8

图4

地震波加速度时程和傅里叶谱"

表2

地震波特性"

地震波持时/s峰值加速度/g卓越频率PF/Hz平均频率MF/Hz
Kobe?1300.8342.781.54
Kobe?2200.3456.301.90
Northridge250.5683.851.82

表3

工况"

上限敏感频率阻尼比
f2=9 SF0.010.020.03
0.040.050.08
0.10
阻尼比敏感频率f2
ζ=0.05SFMF5 SF
PF9 SF13 SF
19 SF

图5

不同阻尼比下测点单元超孔隙水压力比"

图6

不同阻尼比下超孔隙水压力比分布"

图7

不同阻尼比下地铁结构上浮量"

图8

不同阻尼比下地铁结构内力"

图9

不同敏感频率和阻尼比关系"

图10

不同敏感频率下测点单元超孔隙水压力比"

图11

超孔隙水压力比分布"

图12

不同敏感频率下地铁结构上浮量"

Fig.13

Internal force of subway structure considering sensitive frequencies13　不同敏感频率下地铁结构内力"

1 Liu H, Song E. Seismic response of large underground structures in liquefiable soils subjected to horizontal and vertical earthquake excitations[J]. Computers and Geotechnics, 2005, 32(4): 223-244.
2 Zhuang H, Hu Z, Wang X, et al. Seismic responses of a large underground structure in liquefied soils by FEM numerical modelling[J]. Bulletin of Earthquake Engineering, 2015, 13(12): 3645-3668.
3 胡记磊,刘华北. 改进碎石排水措施的地铁结构液化上浮响应数值试验[J]. 隧道建设, 2017, 37(): 82-86.
Hu Ji-lei, Liu Hua-bei. Numerical experiment of liquefaction induced uplift response of metro station by improved gravelly soil method[J]. Tunnel Construction, 2017, 37(Sup.2):82-86.
4 Park D, Hashash Y M A. Soil damping formulation in nonlinear time domain site response analysis[J]. Journal of Earthquake Engineering, 2004, 8(2): 249-274.
5 Kwok A O L, Stewart J P, Hashash Y M A, et al. Use of exact solutions of wave propagation problems to guide implementation of nonlinear seismic ground response analysis procedures[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2007, 133(11): 1385-1398.
6 Hardyniec A, Charney F. An investigation into the effects of damping and nonlinear geometry models in earthquake engineering analysis[J]. Earthquake Engineering & Structural Dynamics, 2015, 44(15): 2695-2715.
7 邹德高,徐斌,孔宪京. 瑞利阻尼系数确定方法对高土石坝地震反应的影响研究[J]. 岩土力学, 2011, 32(3): 797-803.
Zou De-gao, Xu-Bin, Kong Xian-jing. Study of influence of different methods for calculating rayleigh damping coefficient on high earth rock dam seismic response[J]. Rock and Soil Mechanics,2011,32(3):797-803.
8 王豪,高广运,杨成斌. 瑞利阻尼对砂土场地非线性地震响应的影响分析[J]. 地震工程学报, 2016, 38(6): 909-915.
Wang Hao, Gao Guang-yun, Yang Cheng-bin. Influence of rayleigh damping on nonlinear seismic response of sand sites[J]. China Earthquake Engineering Journal, 206, 38(6): 909-915.
9 Tang X W, Shao Q. Numerical simulation on seismic liquefaction by adaptive mesh refinement due to two recovered fields in error estimation[J]. Soil Dynamics and Earthquake Engineering, 2013, 49: 109-121.
10 Tang X W, Zhang X W, Uzuoka R. Novel adaptive time stepping method and its application to soil seismic liquefaction analysis[J]. Soil Dynamics and Earthquake Engineering, 2015, 71: 100-113.
11 Uzuoka R. Analytical study on the mechanical behavior and prediction of soil liquefaction and flow[D]. Gifu: Gifu University, 2000.
12 Oka F, Yashima A, Shibata T, et al. FEM-FDM coupled liquefaction analysis of a porous soil using an elasto-plastic model[J]. Applied Scientific Research, 1994, 52(3): 209-245.
13 Idriss I M, Lysmer J R H. QUAD4: a computer program for evaluating the seismic response of soil structures by variable damping finite element procedures[R]. Berkeley: University of California, 1973.
14 Yoshida N, Kobayashi S, Suetomi I, et al. Equivalent linear method considering frequency dependent characteristics of stiffness and damping[J]. Soil dynamics and Earthquake Engineering, 2002, 22(3): 205-222.
15 Sun Q, Dias D. Significance of Rayleigh damping in nonlinear numerical seismic analysis of tunnels[J]. Soil Dynamics and Earthquake Engineering, 2018, 115: 489-494.
16 Oka F, Yashima A, Tateishi A, et al. A cyclic elasto-plastic constitutive model for sand considering a plastic-strain dependence of the shear modulus[J]. Géotechnique, 1999, 49(5): 661-680.
17 Matsuo O, Shimazu T, Uzuoka R, et al. Numerical analysis of seismic behavior of embankments founded on liquefiable soils[J]. Soils and Foundations, 2000, 40(2): 21-39.
[1] 惠迎新,陈嘉伟. 基于改进遗传算法的挤扩支盘群桩优化方法[J]. 吉林大学学报(工学版), 2023, 53(7): 2089-2098.
[2] 唐亮,司盼,崔杰,凌贤长,满孝峰. 液化微倾场地群桩地震反应分析拟静力方法[J]. 吉林大学学报(工学版), 2022, 52(4): 847-855.
[3] 姜屏,周琳,毛天豪,袁俊平,王伟,李娜. 水泥改性废弃泥浆损伤模型及时间效应[J]. 吉林大学学报(工学版), 2022, 52(12): 2874-2882.
[4] 张飞,朱玉明,杨尚川,王庶懋. 加筋土挡墙碳排放计算方法与减排性分析[J]. 吉林大学学报(工学版), 2021, 51(2): 631-637.
[5] 陶文斌,侯俊领,陈铁林,唐彬. 高预紧力后张法全长锚固支护力学分析[J]. 吉林大学学报(工学版), 2020, 50(2): 631-640.
[6] 高登辉,邢义川,郭敏霞,张爱军,王献涛,马保红. 非饱和重塑黄土⁃混凝土接触面修正双曲线模型[J]. 吉林大学学报(工学版), 2020, 50(1): 156-164.
[7] 古海东,罗春红. 疏排桩-土钉墙组合支护基坑土拱效应模型试验[J]. 吉林大学学报(工学版), 2018, 48(6): 1712-1724.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
版权所有 © 《吉林大学学报(工学版)》编辑部
地址：长春市人民大街5988号　电话：+86-431-85095297　传真：+86-431-85094074　E-mail: xbgxb@jlu.edu.cn
本系统由北京玛格泰克科技发展有限公司设计开发