旋转机械振动频率时间序列预测算法

doi:10.13229/j.cnki.jdxbgxb20210748

摘要/Abstract

摘要：

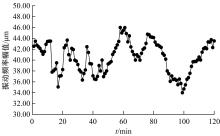
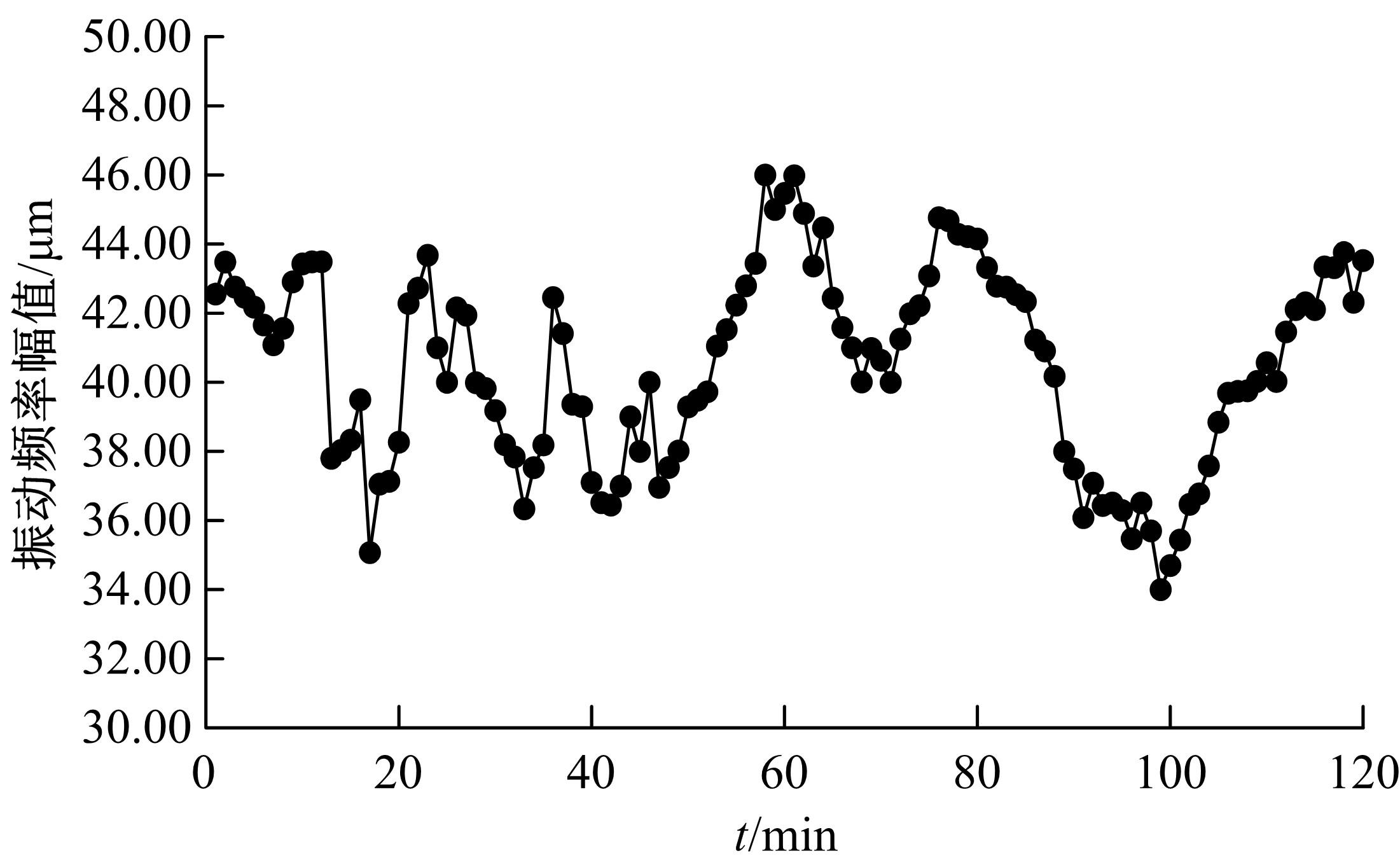
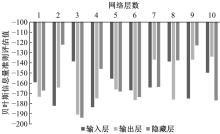
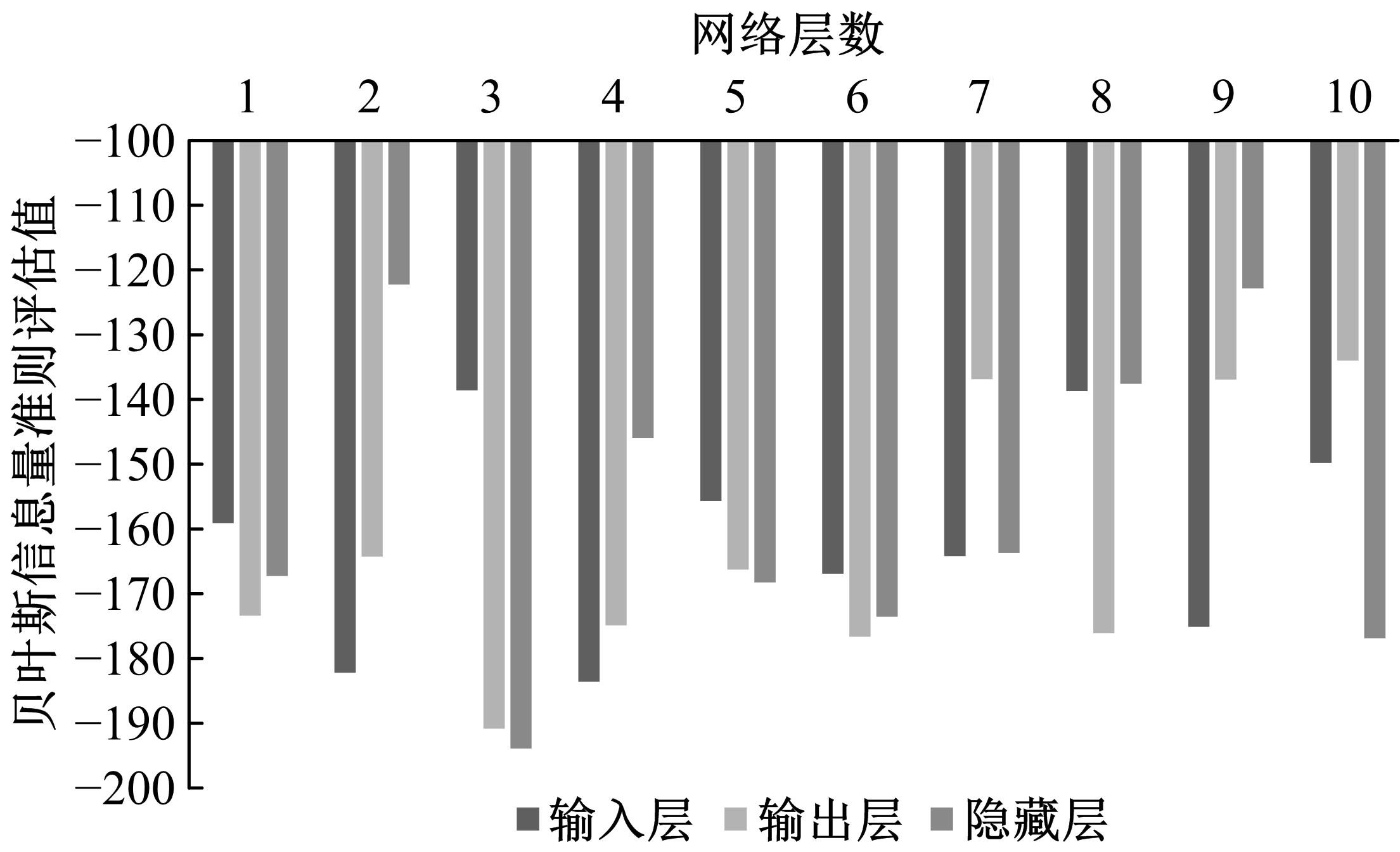
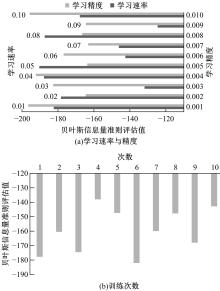
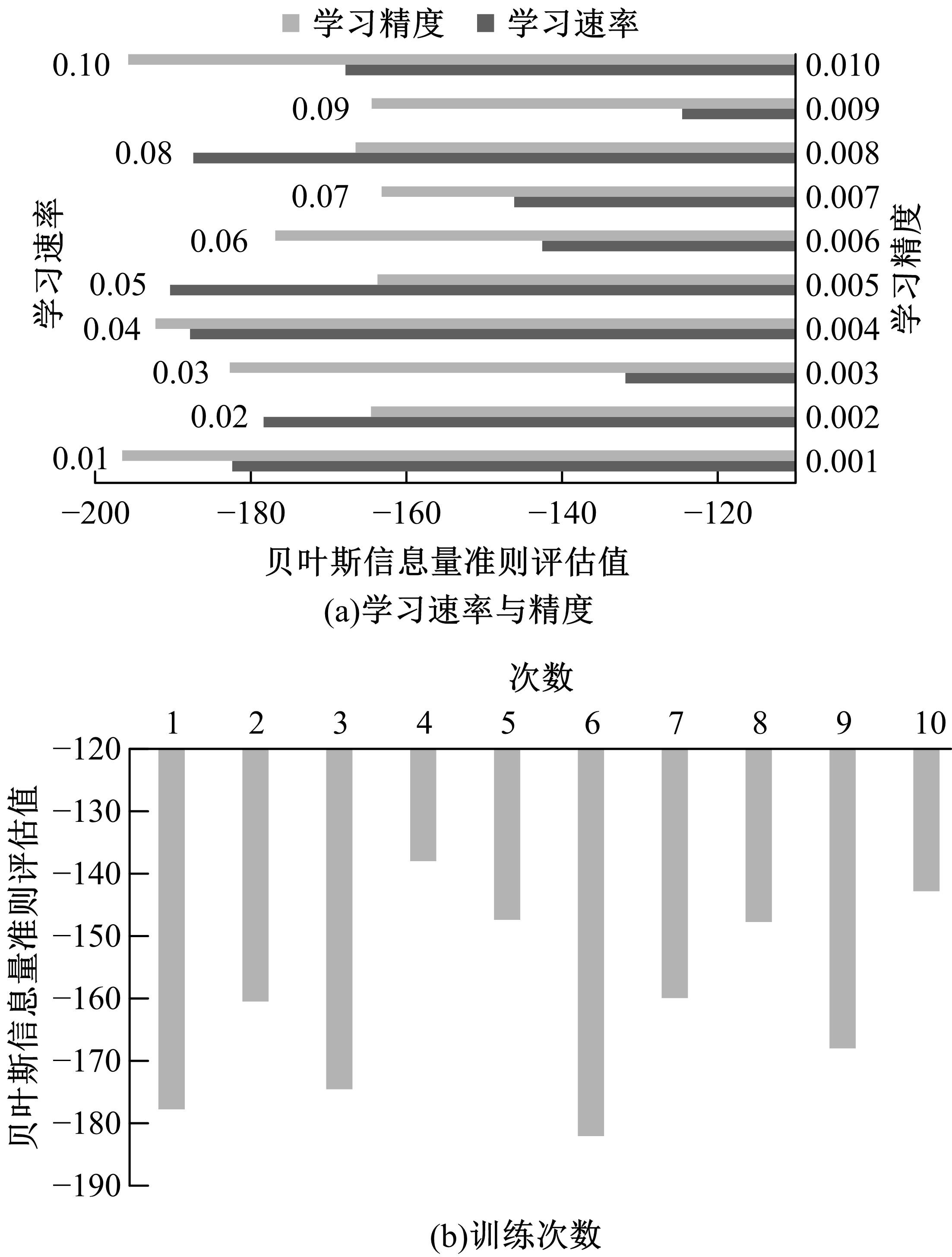
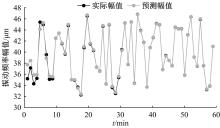
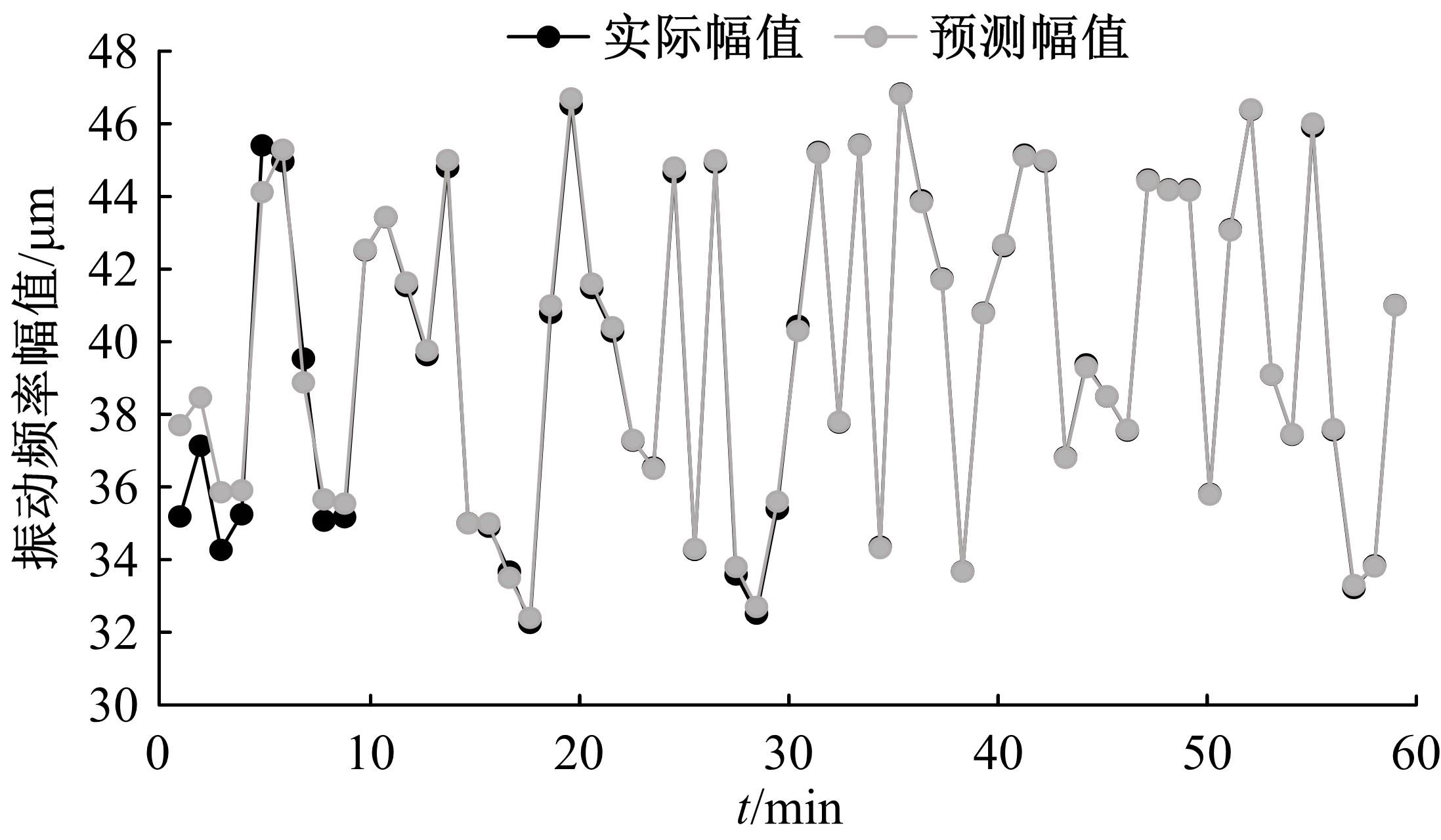
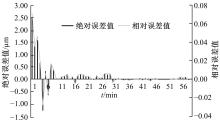
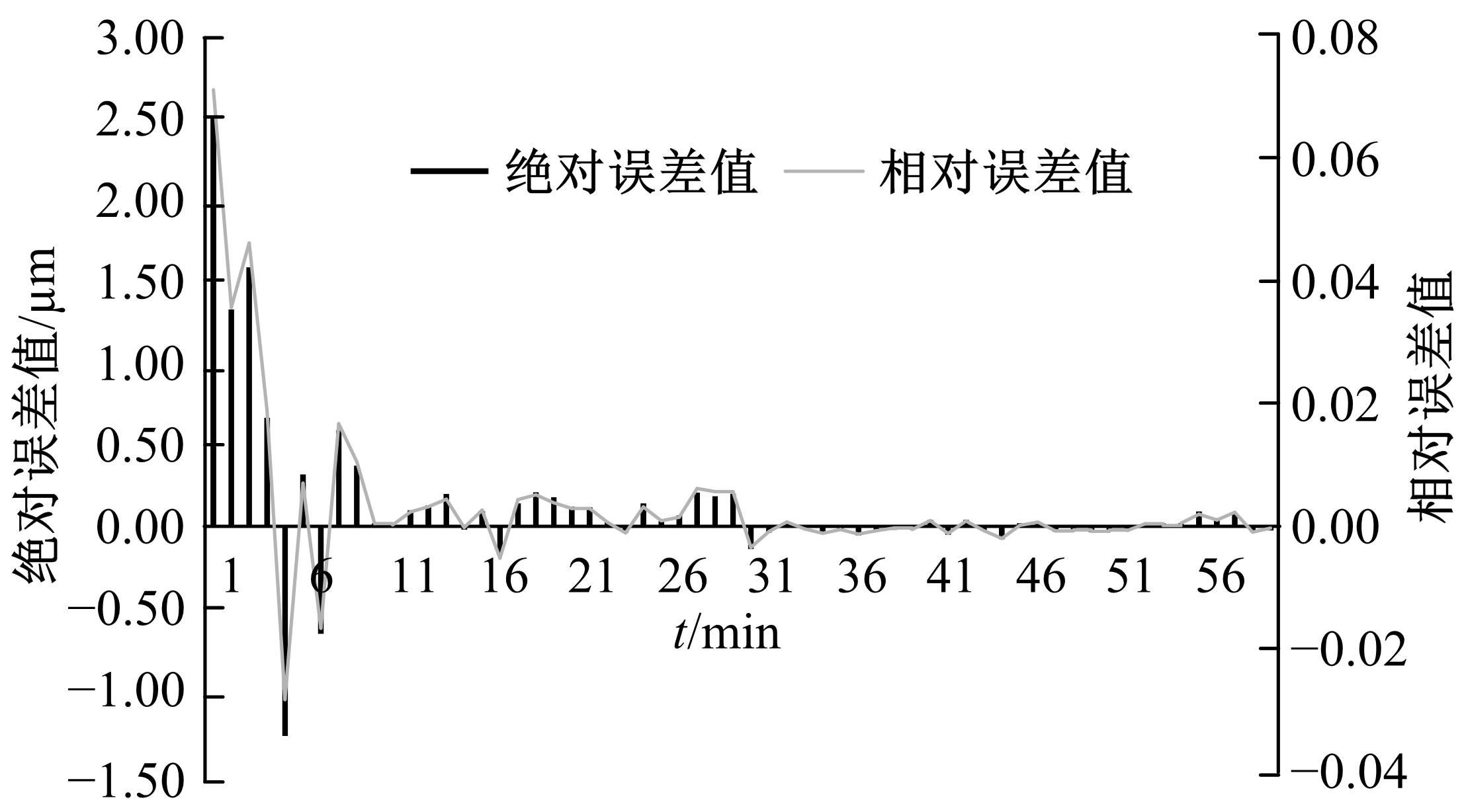
旋转机械设备工作状态时其非平稳特征增加了运行状态预测难度，为此，以神经网络为技术基础，构建了振动频率时间序列预测方法。结合梯度下降法与牛顿法优化反向传播神经网络，针对实际机械振动频率时间序列存在的季节性与趋势性，通过差分法作一阶后向差分处理，推导出自回归序列，得到旋转机械振动频率的时间序列预测模型。在实验环节，面向某电厂汽轮发电机组转子，预测了一小时内振动频率时间序列，在设置网络层数等参数的基础上完成实验，由绝对误差与相对误差值可知，本文方法具备反映振动频率趋势的能力，预测精度较为理想。

关键词: 机电工程, 反向传播神经网络, 旋转机械, 振动频率, 时间序列, 目标函数梯度

Abstract:

The non-stationary characteristics of rotating machinery equipment increase the difficulty of predicting the operating state. Therefore, based on the neural network technology, a vibration frequency time series prediction method is constructed. Combining the gradient descent method and Newton method to optimize the back-propagation neural network， aiming at the seasonality and trend of the time series of actual mechanical vibration frequency， the first-order backward difference is processed by the difference method， the autoregressive sequence is deduced， and the time series prediction model of rotating machinery vibration frequency is obtained. In the experimental link， the vibration frequency time series within one hour is predicted for the rotor of a steam turbine generator unit in a power plant， and the experiment is completed on the basis of setting the parameters such as the number of network layers. From the absolute error and relative error values， the proposed method has the ability to reflect the vibration frequency trend， and the prediction accuracy is ideal.

Key words: electromechanical engineering, back propagation neural network, rotating machinery, vibration frequency, time series, objective function gradient

中图分类号:

TH113

宋震,柳杰. 旋转机械振动频率时间序列预测算法[J]. 吉林大学学报(工学版), 2022, 52(8): 1764-1769.

Zhen SONG,Jie LIU. Time series prediction algorithm of vibration frequency of rotating machinery[J]. Journal of Jilin University(Engineering and Technology Edition), 2022, 52(8): 1764-1769.

图/表 6

图1

图2

图3

表1

图4

图5

参考文献 20

1	翟富刚, 尹燕斌, 李超, 等. 伺服电动缸传动系统刚度建模与前馈控制[J]. 吉林大学学报: 工学版, 2021, 51(2): 442-449.
	Zhai Fu-gang, Yin Yan-bin, Li Chao, et al. Stiffness modeling and feedforward control of servo electric cylinder drive system[J]. Journal of Jilin University(Engineering and Technology Edition), 2021, 51(2): 442-449.
2	Yan X, Jia M. Intelligent fault diagnosis of rotating machinery using improved multiscale dispersion entropy and mRMR feature selection[J]. Knowledge-Based Systems, 2019, 163: 450-471.
3	Casamenti E, Yang T, Vlugter P, et al. Vibration monitoring based on optical sensing of mechanical nonlinearities in glass suspended waveguides[J]. Optics Express, 2021, 29(7): 10853-10862.
4	Hu Y, Cui F, Tu X, et al. Bayesian estimation of instantaneous speed for rotating machinery fault diagnosis[J]. IEEE Transactions on Industrial Electronics, 2020, 68(9): 8842-8852.
5	Song X, Ezzeldin Y H, Caire G, et al. Efficient beam scheduling for half-duplex mmwave relay networks[J]. IEEE Transactions on Communications, 2021, 69(9): 5773-5789.
6	Kim S, Park D J, Chang D E. RAPIDO: a rejuvenating adaptive PID-type optimiser for deep neural networks[J].Electronics Letters,2019, 55(16): 899-901.
7	杨壮, 周渠, 赵耀洪, 等. 基于人工神经网络和多频超声波检测技术的变压器油界面张力预测[J]. 高电压技术, 2019, 45(10): 3343-3349.
	Yang Zhuang, Zhou Qu, Zhao Yao-hong, et al. Prediction of interfacial tension of transformer off based on artificial neural network and multi-frequency ultrasonic testing technology[J]. High Voltage Engineering, 2019, 45(10): 3343-3349.
8	张明光, 蔡云, 丁晶晶. 基于交替迭代法的MMC-MTDC交直流混合系统的潮流分析[J]. 兰州理工大学学报, 2019, 45(6): 91-98.
	Zhang Ming-guang, Cai Yun, Ding Jing-jing. Power flow analysis of MMC-MTDC AC/DC hybrid system based on alternating-iteration method[J]. Journal of Lanzhou University of Technology, 2019, 45(6): 91-98.
9	Cho Y, Farrokhkish M, Norrlinger B, et al. An artificial neural network to model response of a radiotherapy beam monitoring system[J]. Medical Physics, 2020, 47(4): 1983-1994.
10	Pommerenke H W, Heller J, Zadeh S G, et al. Computation of lossy higher order modes in complex SRF cavities using Beyn's and Newton's methods on reduced order models[J]. International Journal of Modern Physics A, 2019, 34(36): 1942037.
11	尹晓丽, 孙凤, 李春明. 连续负梯度方向获得共轭方向的六寻优化方法[J]. 计算机科学与探索, 2019, 13(9): 1604-1612.
	Yin Xiao-li, Sun Feng, Li Chun-ming. Six search optimization method on obtaining conjugate direction after continuous negative gradient directions[J]. Journal of Frontiers of Computer Science & Technology, 2019, 13(9): 1604-1612.
12	Zhu C, Gates D A, Hudson S R, et al. Identification of important error fields in stellarators using the Hessian matrix method[J]. Nuclear Fusion, 2019, 59(12): 126007.
13	张伟, 李焱骏, 师奕兵, 等. 石油管道脉冲远场涡流信号特征分析与处理[J]. 仪器仪表学报, 2019, 40(1): 12-20.
	Zhang Wei, Li Yan-jun, Shi Yi-bing, et al. Feature analysis and processing of pulsed remote field eddy current signal in oil pipes[J]. Chinese Journal of Scientific Instrument, 2019, 40(1): 12-20.
14	杨德磊, 童乐为. 支管受轴向受拉工况下CHS-CFSHS T型节点应力集中系数计算公式[J]. 吉林大学学报: 工学版, 2019, 49(6): 1891-1899.
	Yang De-lei, Tong Le-wei. Calculation formula of SCF for CHS-CFSHS welded T-joints with brace under axial tension[J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(6): 1891-1899.
15	Melnyk S S, Yampol'Skii V A, Usatenko O V. Continuous stochastic processes with non-local memory[J]. Physical Review E, 2019(4): 1-7.
16	Han S, Rajendran S. Comparison of time series methods and machine learning algorithms for forecasting taiwan blood services foundation's blood supply[J/OL]. [2021-05-18].
17	张姝玮, 郭忠印, 陈立辉.基于自回归求积移动平均的制动器温度预测方法[J]. 吉林大学学报: 工学版, 2020, 50(6): 2080-2086.
	Zhang Shu-wei, Guo Zhong-yin, Chen Li-hui. Brake temperature prediction method based on autoregressive integrated moving average model[J]. Journal of Jilin University(Engineering and Technology Edition), 2020, 50(6): 2080-2086.
18	赵志文, 杨慧超, 彭毳鑫. 自回归模型偏自相关函数截尾性检验[J]. 统计与决策, 2019, 35(8): 5-8.
	Zhao Zhi-wen, Yang Hui-chao, Peng Xiao-xin. Truncation test of partial autocorrelation function for autoregressive model[J]. Statistics and Decision, 2019, 35(8): 5-8.
19	罗忠涛, 詹燕梅, 郭人铭, 等. 脉冲噪声中基于指数函数的可变拖尾非线性变换设计[J]. 电子与信息学报, 2020, 42(4): 932-940.
	Luo Zhong-tao, Zhan Yan-mei, Guo Ren-ming, et al. Variable tailing nonlinear transformation design based on exponential function in impulsive noise[J]. Journal of Electronics & Information Technology, 2020, 42(4): 932-940.
20	Zhao Y, Ke X, Huang L, et al. On cycle-period estimation: a Bayesian information criterion[J]. IEEE Transactions on Vehicular Technology, 2021, 70(4): 3949-3954.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

名称	数值
输入层单元数量	4
输出层单元数	3
隐藏层数	3
学习速率	0.05
学习精度	0.001
网络训练次数	6

[1]	谭永营,伊善贞,薛大兵,王晓明,袁磊. 负载型四足步行平台对角步态重量自适应行走控制[J]. 吉林大学学报(工学版), 2021, 51(4): 1506-1517.
[2]	董延华,刘靓葳,赵靖华,李亮,解方喜. 基于BPNN在线学习预测模型的扭矩实时跟踪控制[J]. 吉林大学学报(工学版), 2021, 51(4): 1405-1413.
[3]	刘舒, 姜琦刚, 朱航, 李晓东. 基于Hyb-F组合滤波算法的向海自然保护区NDVI时间序列重构[J]. 吉林大学学报(工学版), 2018, 48(3): 957-967.
[4]	万平, 吴超仲, 林英姿, 马晓凤. 基于驾驶行为多元时间序列特征的愤怒驾驶状态检测[J]. 吉林大学学报(工学版), 2017, 47(5): 1426-1435.
[5]	王寅同, 王建东, 陈海燕. 时间序列降维及机场噪声中的机型识别[J]. 吉林大学学报(工学版), 2016, 46(4): 1202-1208.
[6]	王石, 隋永新, 董琰, 杨怀江. 基于改进型小数据量法的局域网流量预测[J]. 吉林大学学报(工学版), 2016, 46(4): 1254-1260.
[7]	郑寇全,雷英杰,王睿,余晓东. 基于矢量量化的长期直觉模糊时间序列预测[J]. 吉林大学学报(工学版), 2014, 44(3): 795-780.
[8]	刘寒冰, 李国恒, 谭国金, 孙晏一. 基于时间序列的边坡位移实时预测方法[J]. 吉林大学学报(工学版), 2012, 42(增刊1): 193-197.
[9]	张勇, 关伟. 预测交通流量时间序列的组合动态建模方法[J]. 吉林大学学报(工学版), 2010, 40(05): 1209-1214.
[10]	赵志强,张毅,胡坚明. 基于GTM-TT算法的城市区域交通状态分析[J]. 吉林大学学报(工学版), 2009, 39(增刊2): 1-0006.
[11]	赵丁选，崔功杰，陈宁，张红彦 . 基于BP神经网络的工程车辆四参数自动变速控制[J]. 吉林大学学报(工学版), 2008, 38(05): 1091-1094.
[12]	廖庆斌，李舜酩，覃小攀 . 车辆振动信号的特征提取方法比较[J]. 吉林大学学报(工学版), 2007, 37(04): 910-915.