基于空间网格分析的多箱室波形钢腹板组合梁腹板剪力分配

doi:10.13229/j.cnki.jdxbgxb20170719

摘要/Abstract

摘要：

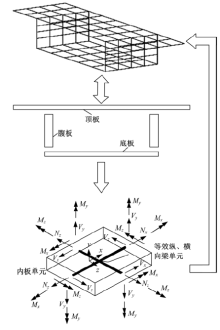
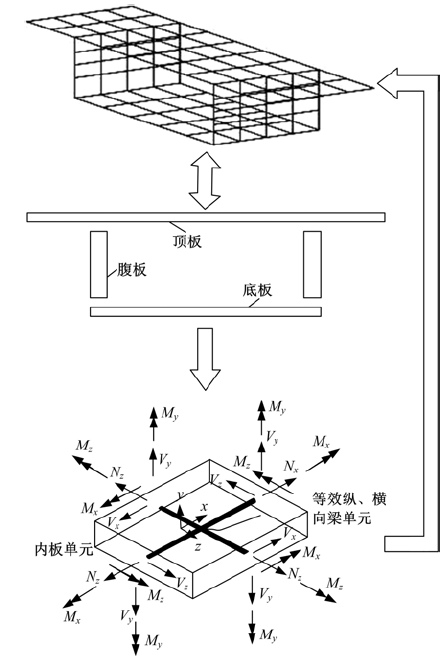
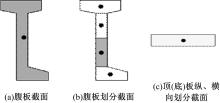
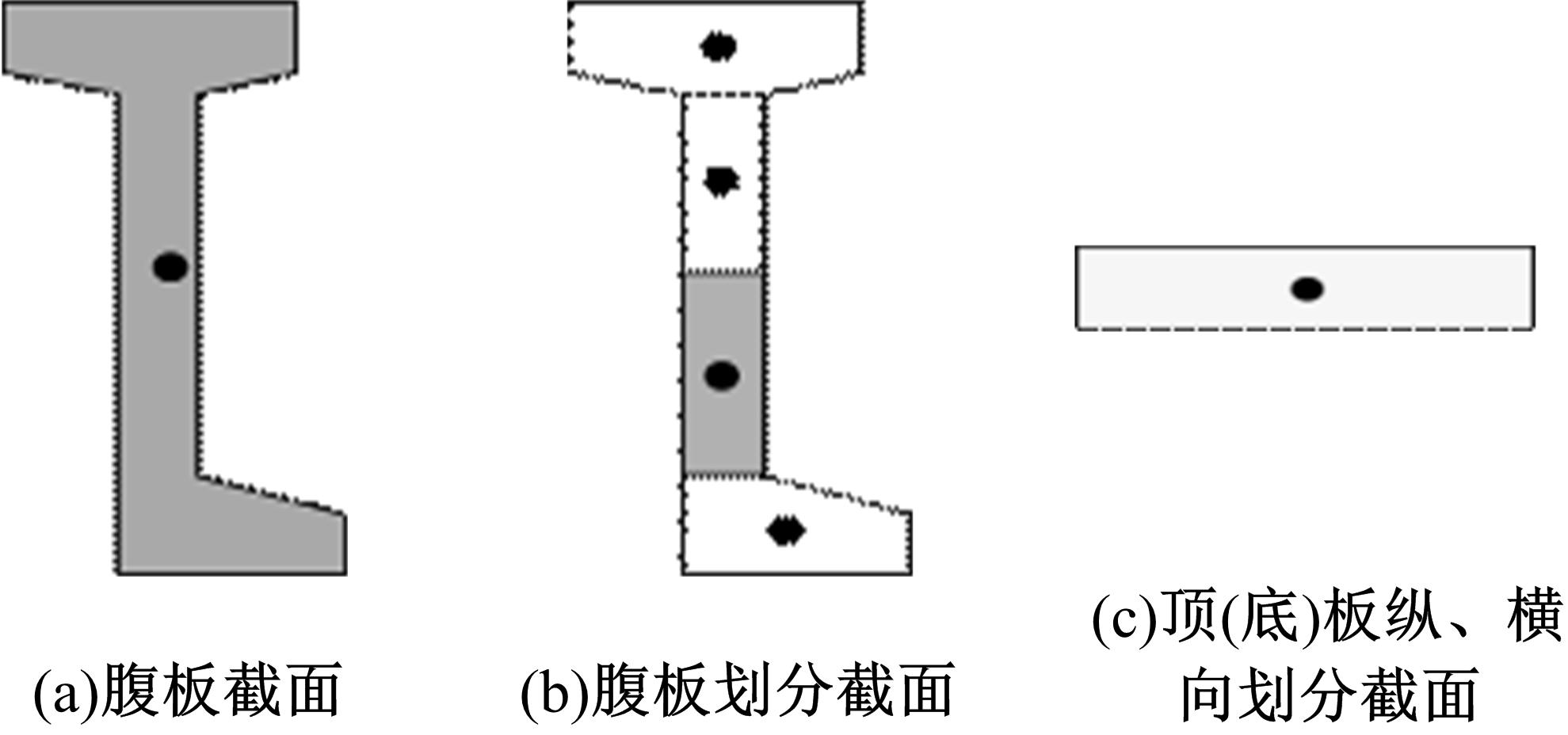
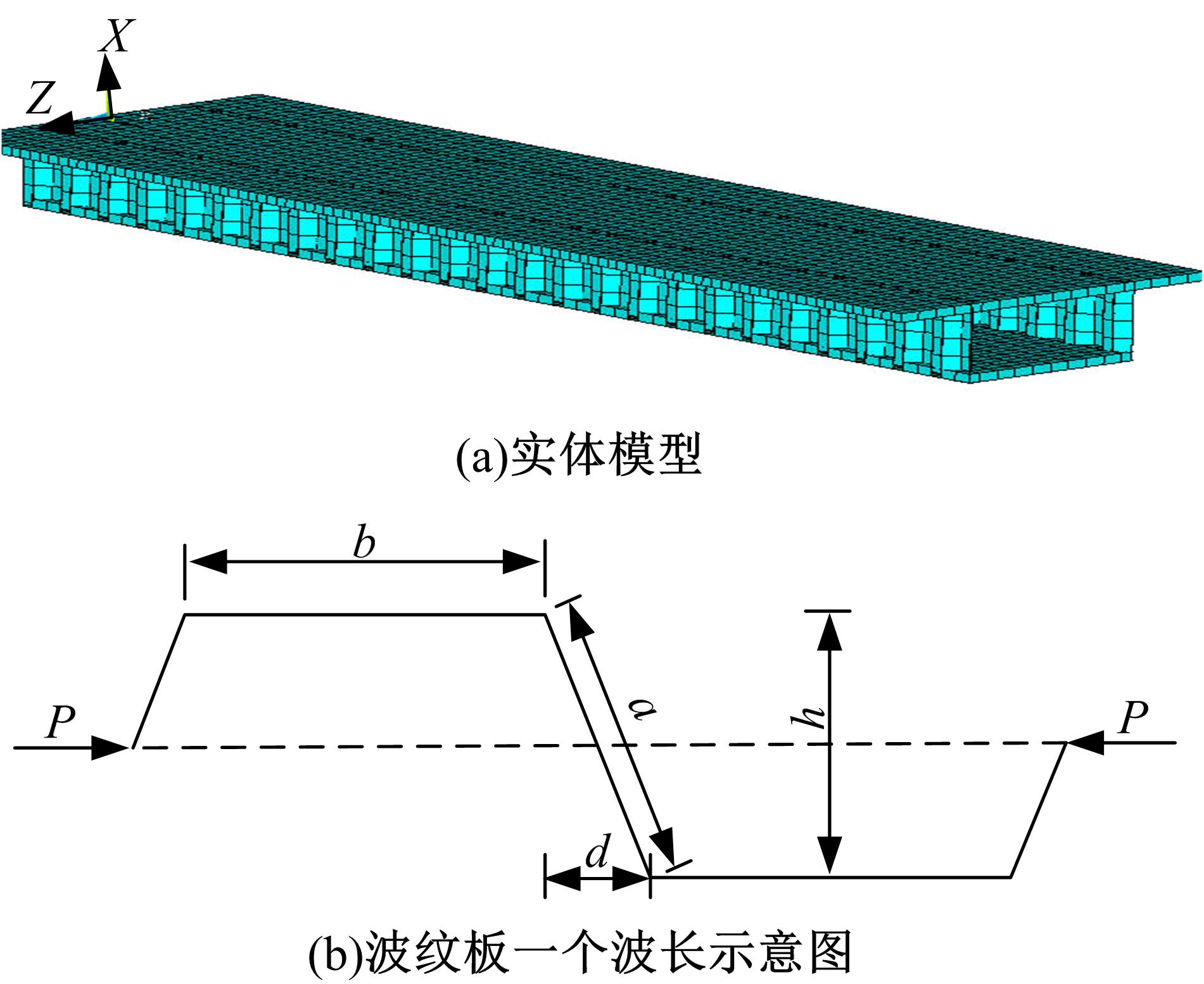
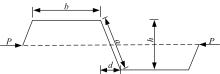
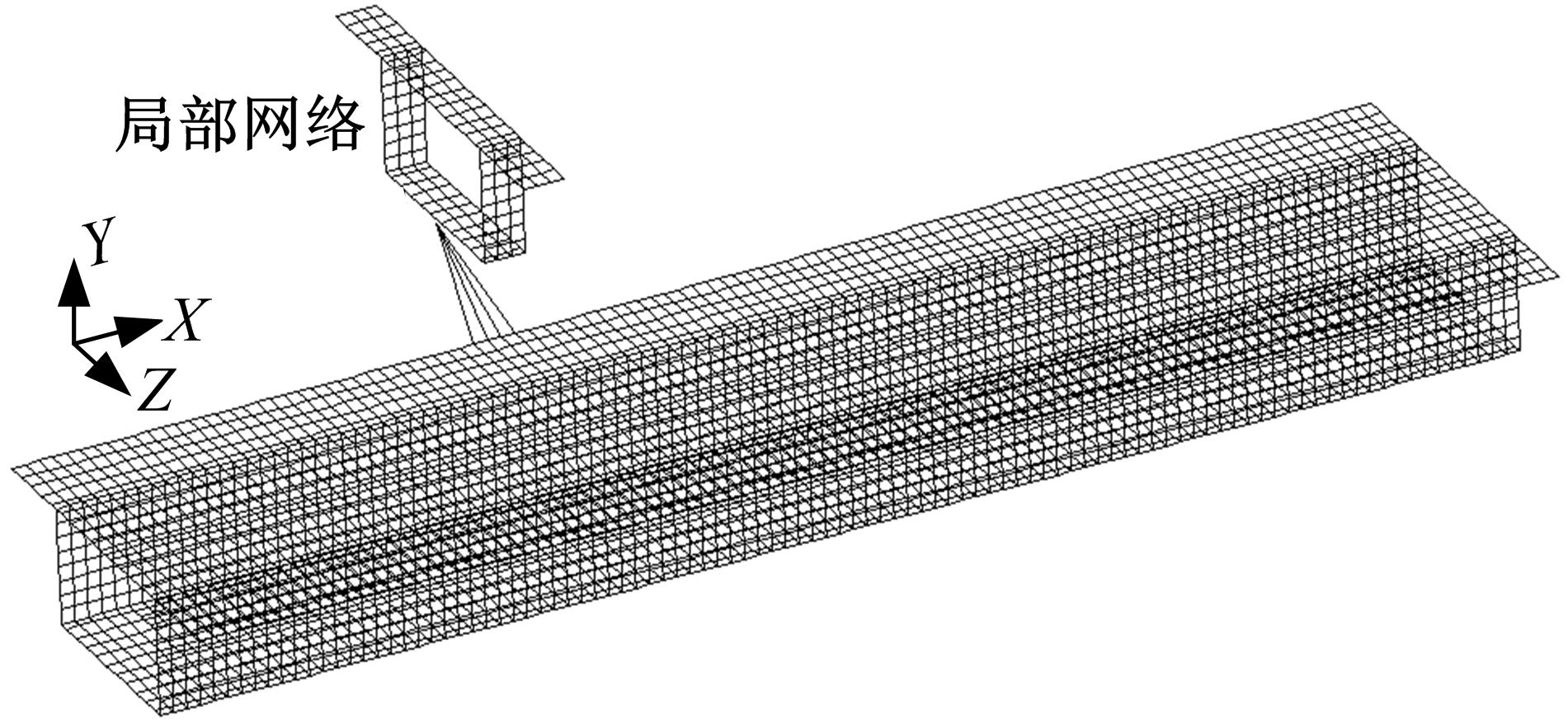
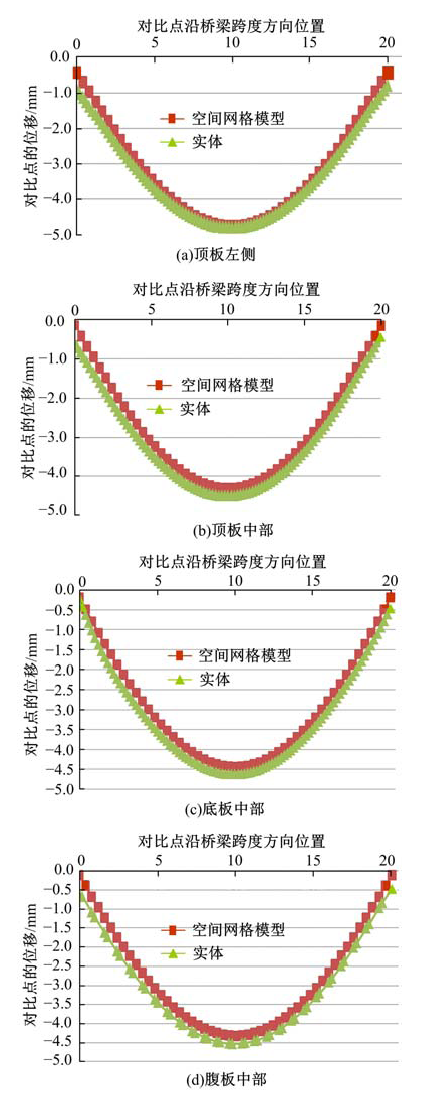
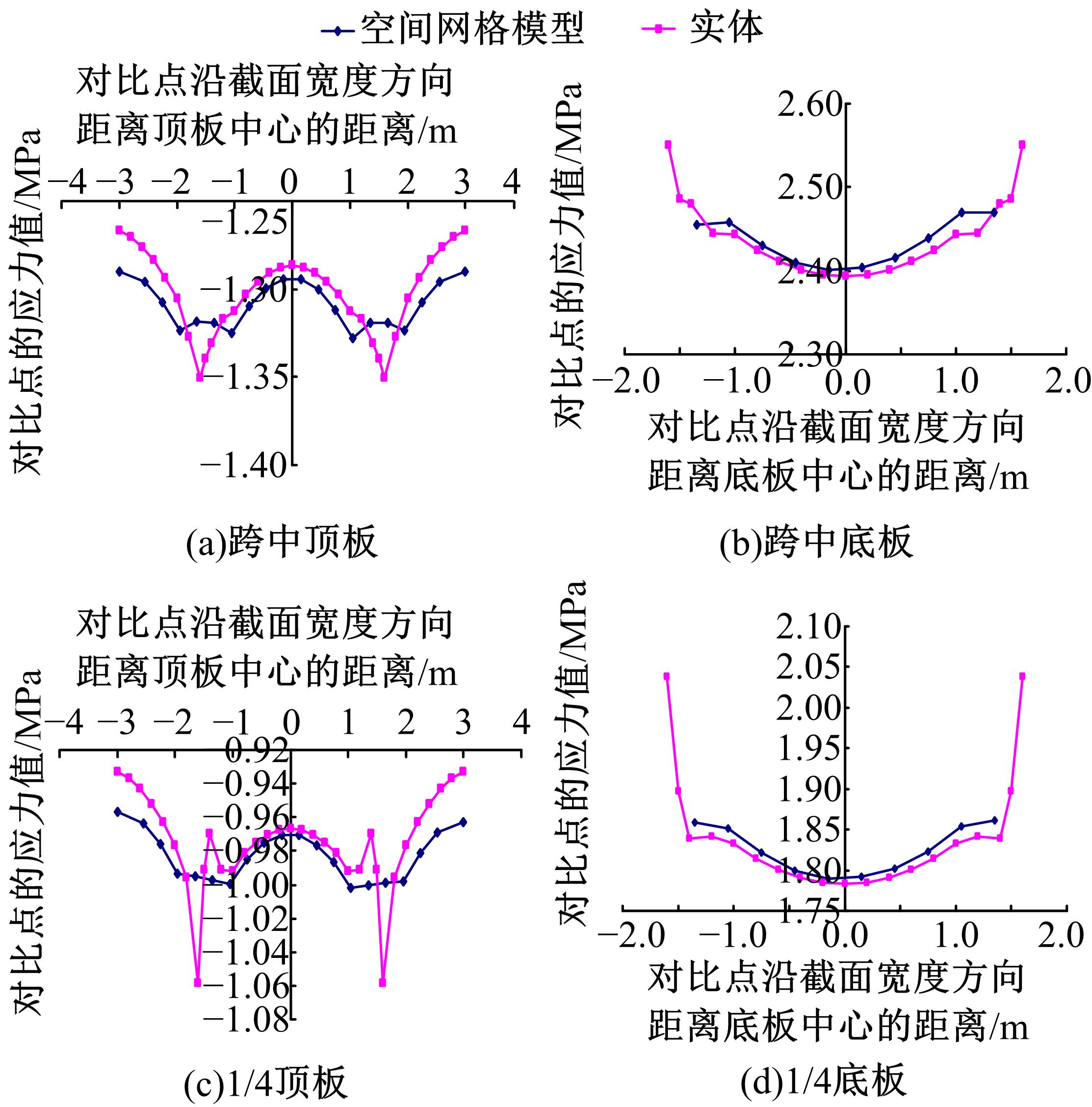
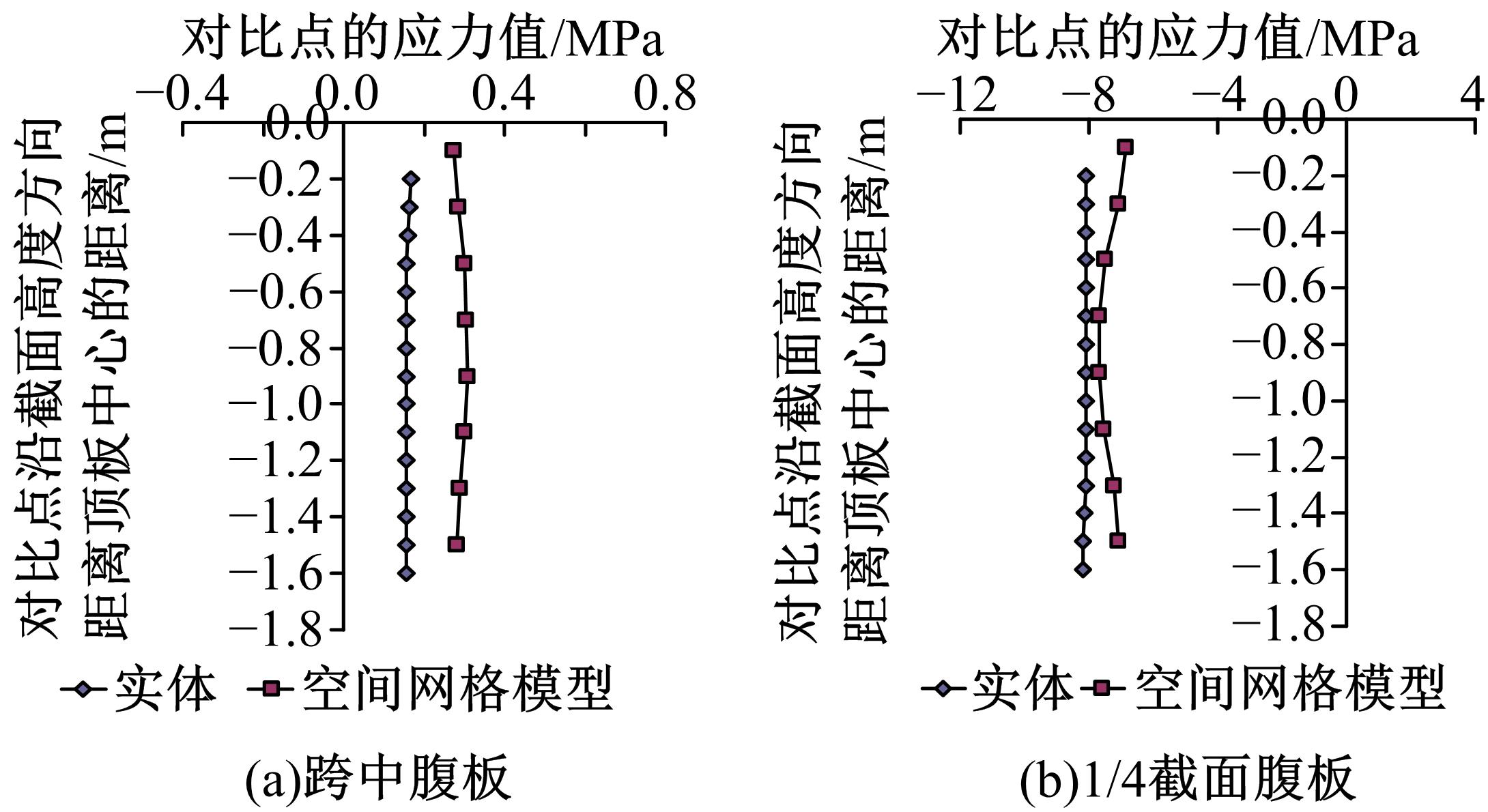
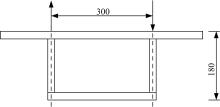
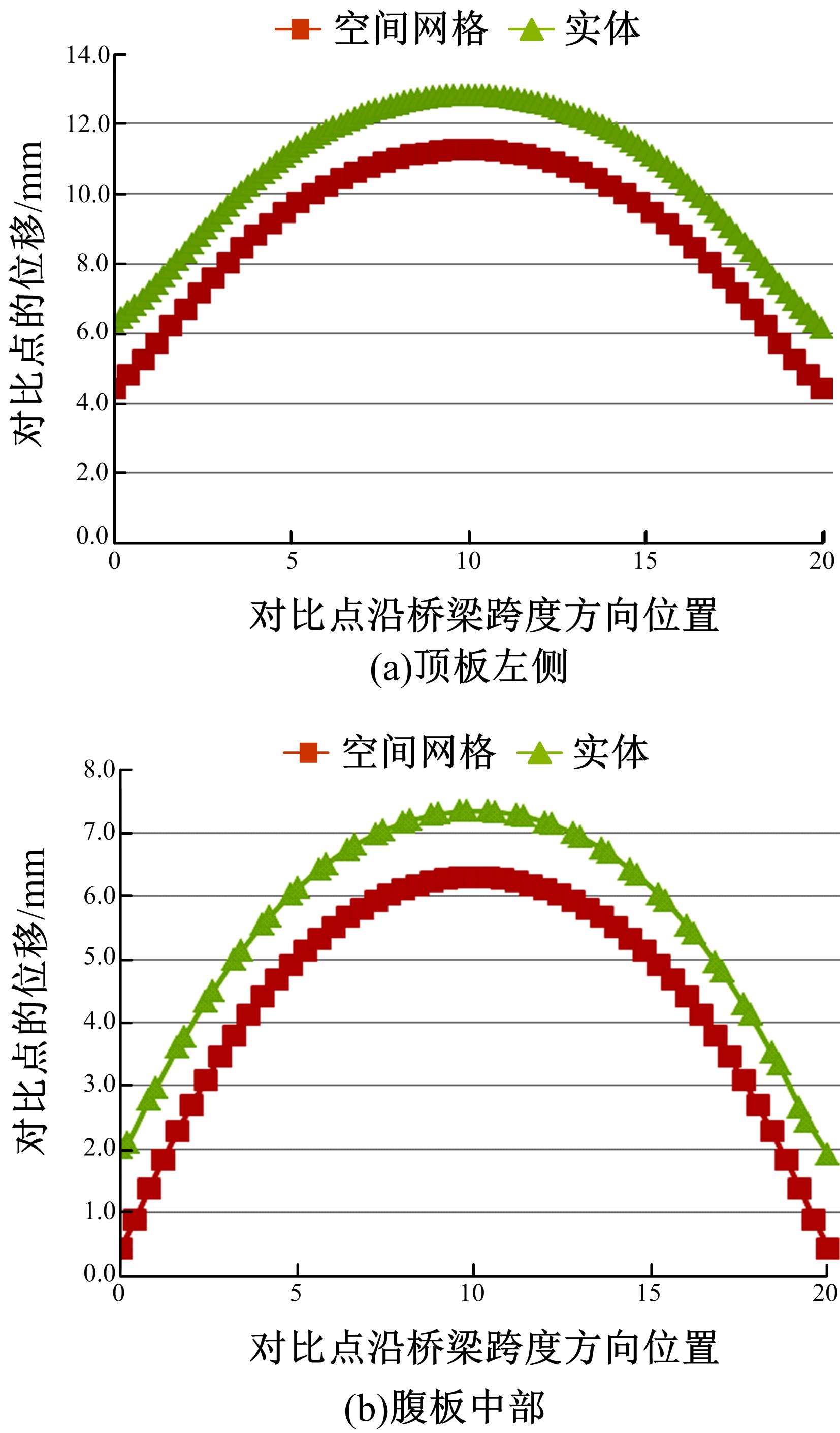
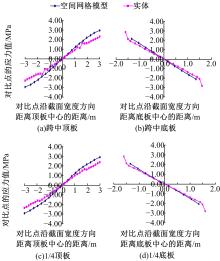
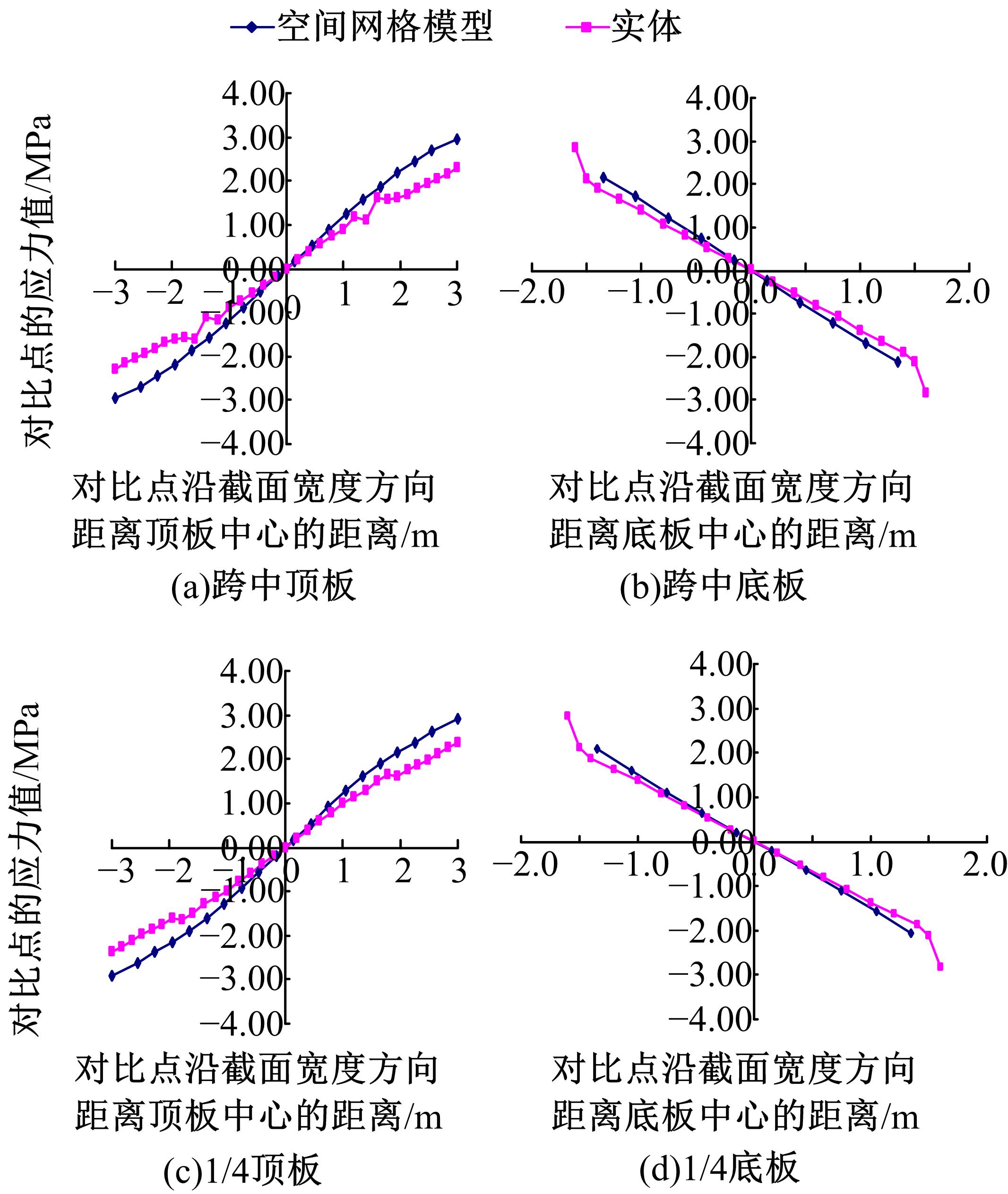
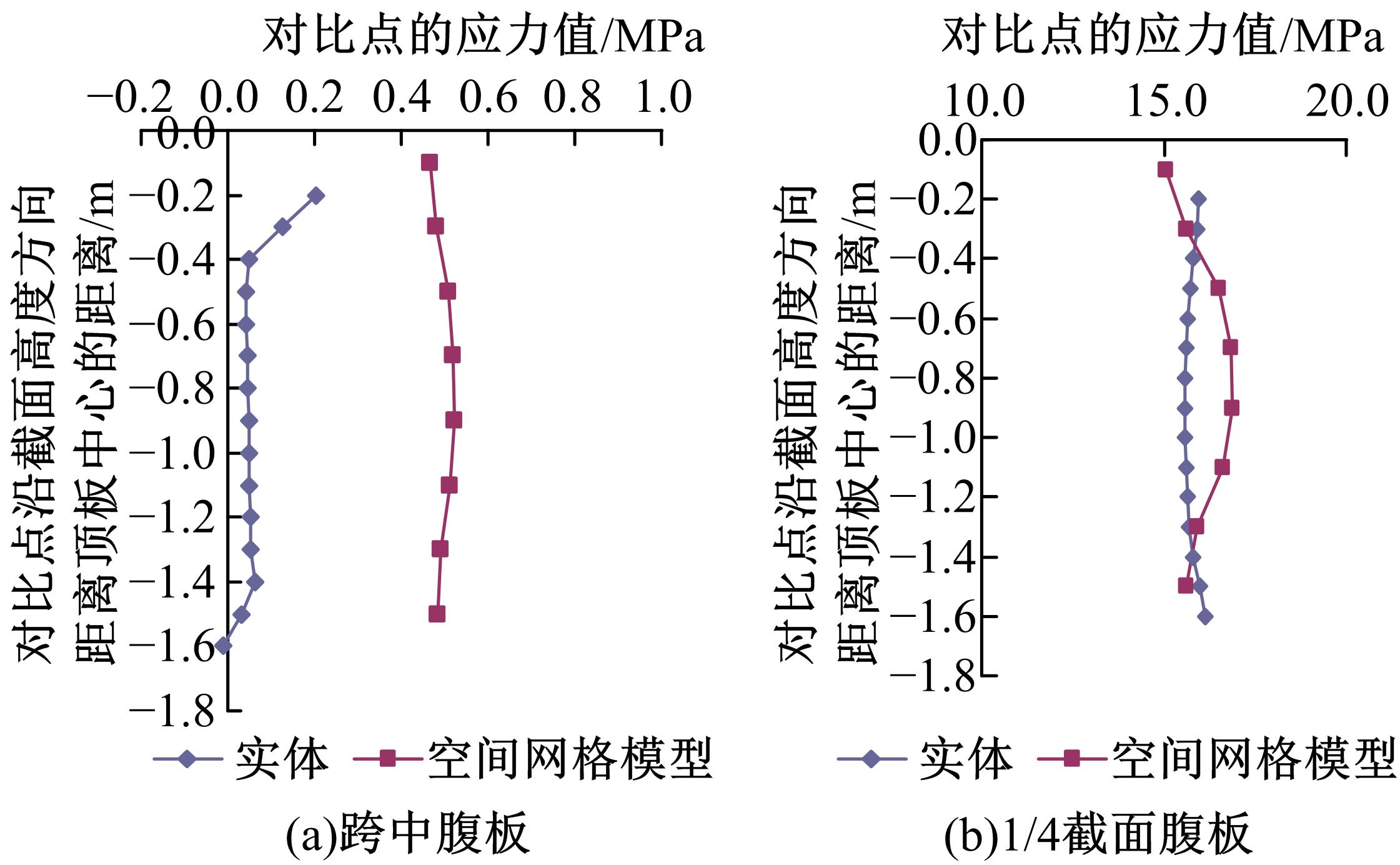
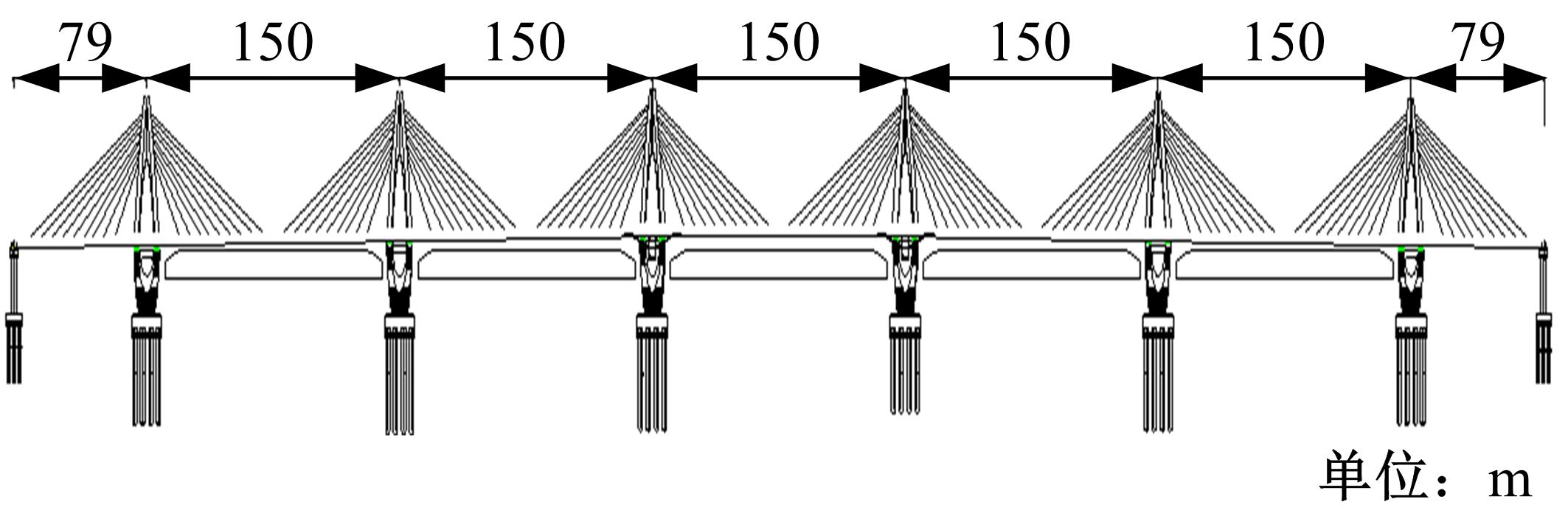
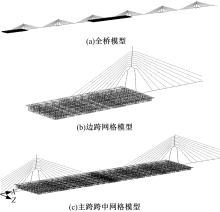
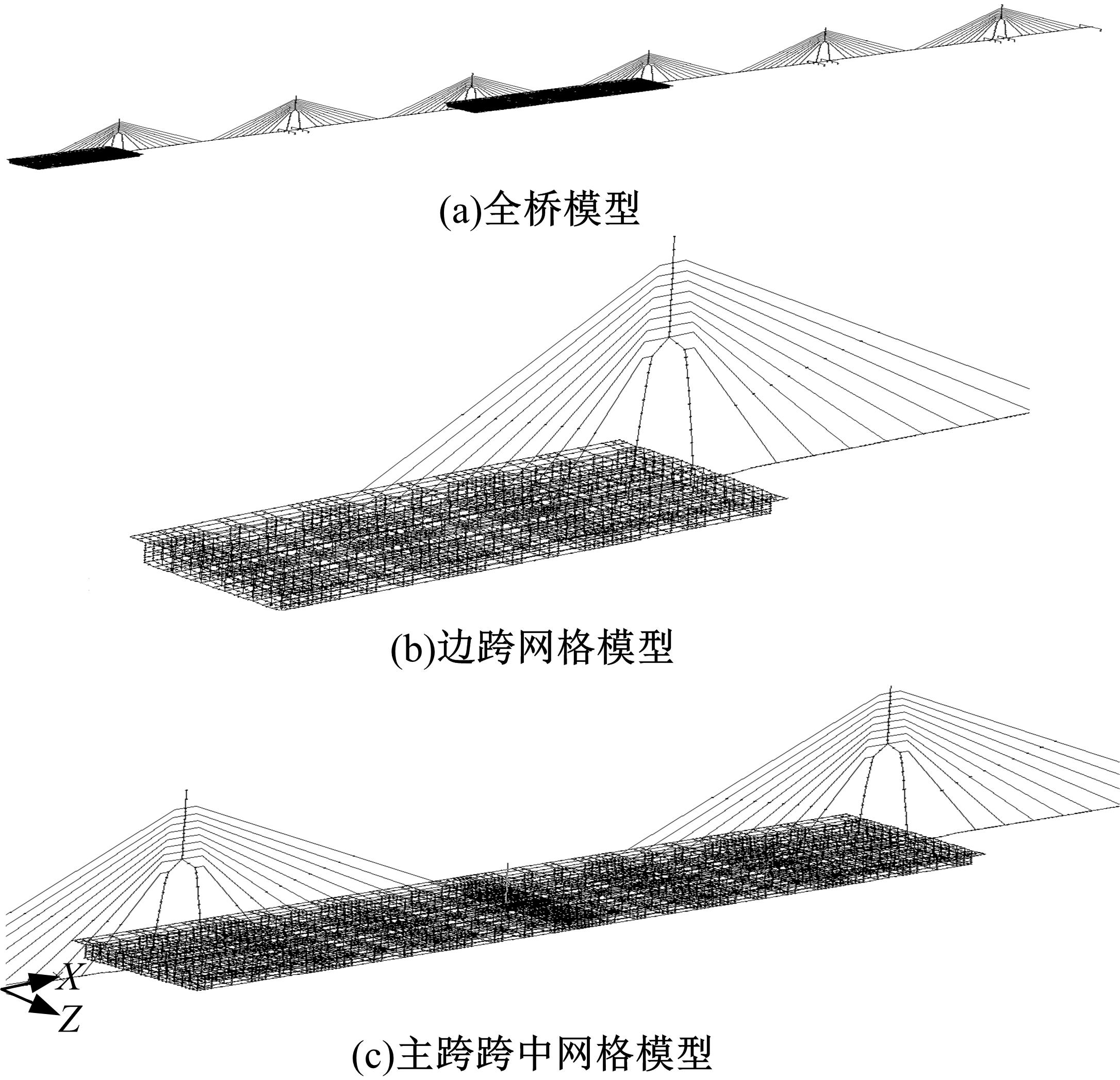
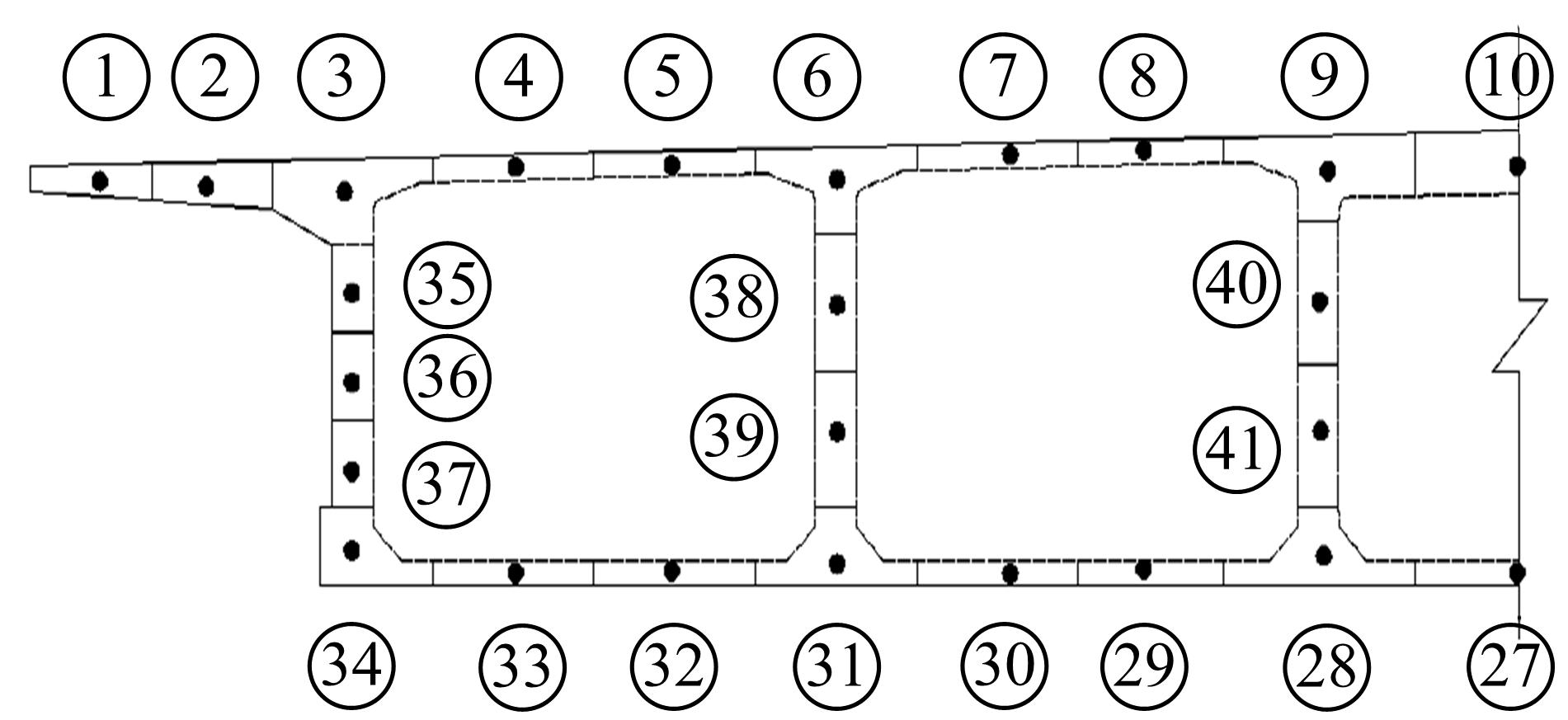
针对多箱室波形钢腹板组合梁桥设计中空间杆系模型缺乏空间效应精细化分析,平面梁格法在等效原理上的近似性不能准确反映箱形组合梁的剪应力分布和顶底板局部受力,以及实体模型很难与总体计算相结合的缺点,提出采用空间网格分析方法进行多箱室波形钢腹板组合梁腹板组合梁桥剪力分配。实例分析结果表明:空间网格模型可以将各道腹板剪力横向分配全部算清楚,且得出了斜拉桥边中跨的关键截面横梁处各道腹板剪力分配规律,为此类工程设计提供了一定的参考价值。

关键词: 工程力学, 波形钢腹板, 组合梁斜拉桥, 多箱室, 空间网格模型, 精细化分析

Abstract:

The composite girder bridge with multi-cell corrugated steel web has been widely used in recent years, but there are some deficiencies in the corresponding specification and fine calculation methods. At present, the design mostly adopts the computational analytical method combining the spatial bar system model, plane beam grillage model and solid model. However, the spatial bar system model is short of the refinement analysis on the space effect, such as the shear lag effect, effective distribution width problem, and eccentric load factor problem etc. Due to the similarity of the plane beam grillage method in the equivalence principle, it can not accurately reflect the shearing stress distribution and local stress of the top and bottom plates of the box type composite beam. The solid model is very difficult to combine with the overall calculation. Moreover, the spatial grid model can achieve the refinement analysis, with the integrity of the analysis and the comprehensiveness of the stress checking calculation, and can make up the deficiency of the analytical method currently. Through the example verification of the solid model and spatial grid model, it can be seen that the calculation results for the stress and the displacement of two models are almost consistent, indicating the applicability and precision of the grid model.The real bridge analysis shows that the space grid model of multiple chamber box girder with corrugated steel webs can be calculated the web shear transverse distribution clearly, and the each web shear distribution rules of cable-stayed bridge at the key sections of side and mid span, so it can provide some suggestions for this kind of engineering design.

Key words: engineering mechanics, corrugated steel web, composite beam cable-stayed bridge, multi-cell, spatial grid model, refined analysis

中图分类号:

TU318

尼颖升,孙启鑫,马晔,徐栋,刘超. 基于空间网格分析的多箱室波形钢腹板组合梁腹板剪力分配[J]. 吉林大学学报(工学版), 2018, 48(6): 1735-1746.

NI Ying-sheng,SUN Qi-xin,MA Ye,XU Dong,LIU Chao. Shear distribution of multi-cell corrugated steel web composite beams based on space grid analysis[J]. Journal of Jilin University(Engineering and Technology Edition), 2018, 48(6): 1735-1746.

图/表 30

图1

图2

图3

图4

图5

图6

图7

图8

图9

图10

图11

图12

图13

图14

图15

图16

图17

图18

图19

图20

图21

图22

表2

表3

表5

表6

表7

表8

参考文献 13

[1]	肖湘, 黄恩厚, 尼颖升 . 预应力混凝土梁板体系有效翼缘的理论分析及试验[J]. 吉林大学学报:工学版, 2015,45(6):1784-1790. doi: 10.13229/j.cnki.jdxbgxb201506008
	Xiao Xiang, Huang En-hou, Ni Ying-sheng . Theoretic analysis and experimental study of effective flange width on beam-plates system of prestressed concrete[J]. Journal of Jilin University(Engineering and Technology Edition), 2015,45(6):1784-1790. doi: 10.13229/j.cnki.jdxbgxb201506008
[2]	Jung K H, Kim K S, Sim C W , et al. Verification of incremental launching construction safety for the llsun bridge:the world's longest and widest prestressed concrete box girder with corrugated steel web section[J]. Journal of Bridge Engineering, 2011,16(3):453-460. doi: 10.1061/(ASCE)BE.1943-5592.0000165
[3]	Li Guo-qiang, Wang Wei-yong . A simplified approach for fire-resistance design of steel-concretecomposite beams[J]. Steel and Composite Structures, 2013,14(3):295-312. doi: 10.12989/scs.2013.14.3.295
[4]	贺君 . 波折钢腹板组合桥梁力学性能与设计方法研究[D]. 上海:同济大学土木工程学院, 2011.
	He Jun . Mechanical performance and design method of composite bridge with corrugated steel webs[D]. Shanghai:School of Civil Engineering, Tongji University, 2011.
[5]	Nguyen N D, Kim S N, Han S R , et al. Elastic lateral-torsional buckling strength of I-girder with trapezoidal web corrugations using a new warping constant under uniform moment[J]. Engineering Structures, 2010,32(8):2157-2165. doi: 10.1016/j.engstruct.2010.03.018
[6]	Liu Chao, Xu Dong . Space frame lattice model for stress analysis of bridge[J]. The Baltic Journal of Road and Bridge Engineering, 2010,5(2):98-103. doi: 10.3846/bjrbe.2010.14
[7]	Liu Chao, Xu Dong . Influence of cracking on deflections of concrete box girder bridges[J]. Baltic Journal of Road and Bridge Engineering, 2012,7(2):104-111. doi: 10.3846/bjrbe.2012.15
[8]	徐栋, 赵瑜, 刘超 . 混凝土桥梁的实用精细化分析与设计[M]. 北京: 人民交通出版社, 2013.
[9]	Xu Dong, Zhao Yu. Application of spatial grid model in structural analysis of concrete box girder bridges [C]//18th Congress of International Association for Bridge and Structural Engineering, Seoul, 2012: 2009-2016.
[10]	ValsaIpe T, Sharada B H, Manjula V K , et al. Flexural behavior of cold-formed steel concrete composite beams[J]. Steel and Composite Structures, 2013,14(2):105-120. doi: 10.12989/scs.2013.14.2.105
[11]	Mo Y L, Fan Y L . Torsional design of hybrid concrete box girders[J]. Journal of Bridge Engineering, 2006,11(3):329-339. doi: 10.1061/(ASCE)1084-0702(2006)11:3(329)
[12]	Machimdamrong C, Watanabe E, Utsunomiya T . Analysis of corrugated steel web girders by an efficient beam bending theory[J]. Structural Engineering/Earthquake Engineering, 2004,21(2):131-142. doi: 10.2208/jsceseee.21.131s
[13]	Huang L, Hikosaka H, Komine K . Simulation of accordion effect in corrugated steel web with concrete flanges[J]. Computers and Structures, 2004,82(23-26):2061-2069. doi: 10.1016/j.compstruc.2003.07.010

相关文章 15

[1]	马晔, 尼颖升, 徐栋, 刁波. 基于空间网格模型分析的体外预应力加固[J]. 吉林大学学报(工学版), 2018, 48(1): 137-147.
[2]	尼颖升, 孙启鑫, 马晔, 徐栋. 基于拉应力域的波形钢腹板组合梁承载力配筋计算[J]. 吉林大学学报(工学版), 2018, 48(1): 148-158.
[3]	尼颖升, 马晔, 徐栋, 李金凯. 波纹钢腹板斜拉桥剪力滞效应空间网格分析方法[J]. 吉林大学学报(工学版), 2017, 47(5): 1453-1464.
[4]	闫亚宾, 王晓媛, 万强. 纳米尺度界面低周疲劳破坏行为[J]. 吉林大学学报(工学版), 2017, 47(4): 1201-1206.
[5]	陈江义, 刘保元. 纤维断裂损伤对复合材料板中导波频散特性的影响[J]. 吉林大学学报(工学版), 2017, 47(1): 180-184.
[6]	孟广伟, 冯昕宇, 周立明, 李锋. 基于降维算法的结构可靠性分析[J]. 吉林大学学报(工学版), 2017, 47(1): 174-179.
[7]	杨慧艳, 何晓聪, 周森. 压印接头强度的有限元模型及理论计算方法[J]. 吉林大学学报(工学版), 2015, 45(3): 864-871.
[8]	张庆, 王磊. 基于微分方程组的多排桩内力分析[J]. 吉林大学学报(工学版), 2014, 44(5): 1327-1333.
[9]	赵世佳, 徐涛, 陈炜, 谭丽辉. 接近亏损系统模态灵敏度分析的有效算法[J]. 吉林大学学报(工学版), 2013, 43(增刊1): 497-499.
[10]	徐涛, 赵世佳, 张炜, 谭丽辉, 吕岗, 李恒. N重亏损系统摄动的原点移位组合近似方法[J]. 吉林大学学报(工学版), 2012, 42(增刊1): 147-150.
[11]	闫光, 范舟, 李钟海, 程小全, 刘克格, 左春柽. 复合材料加口盖柱壳的设计与分析[J]. , 2012, (06): 1437-1441.
[12]	李春良^1,2,王国强¹,刘福寿³,赵凯军⁴. 盾构管片结构的力学行为分析[J]. 吉林大学学报(工学版), 2011, 41(6): 1669-1674.
[13]	张道明¹,郭学东²,赵志蒙³. 钢筋混凝土梁弯曲损伤分析的摄动法[J]. 吉林大学学报(工学版), 2011, 41(05): 1358-1363.
[14]	陈耕野, 王彦召, 姚战卫. 平行弦钢桁架应力与感应电动势随荷载的变化[J]. 吉林大学学报(工学版), 2010, 40(增刊): 222-0227.
[15]	贾超, 纪圣振, 张峰. 青岛海湾大桥混凝土墩的时变可靠度[J]. 吉林大学学报(工学版), 2010, 40(06): 1543-1549.

Metrics

Viewed

Full text

Abstract

Cited

Shared

Discussed

	加密区段	外腹板	内腹板	中腹板	大致比例
1号索	1#横梁	88.25	-46.9	217	1:0.53:2.45
	2#横梁	320.34	298	-754.5	1:0.91:2.36
	3#横梁	537	403.9	-1612.5	1:0.75:3.0
	4#横梁	173.7	-164.52	-653.5	1:0.95:3.76
5号索	1#横梁	-55.2	123.45	143.975	1:2.24:2.61
	2#横梁	180.07	217.99	-672.44	1:1.21:3.73
	3#横梁	394.57	273.4	-1271.92	1:0.69:3.22
	4#横梁	-168.13	120.52	179.96	1:0.72:1.07
9号索	1#横梁	-887.74	-576.64	1043.44	1:0.64:1.18
	2#横梁	-474.75	-448.52	450.36	1:0.94:0.95
	3#横梁	-559.76	-284.98	-536.92	1:0.51:0.96
	4#横梁	-438.47	-288.14	-305.57	1:0.66:0.70

	加密区段	外腹板	内腹板	中腹板	大致比例
1号索	1#横梁	-175.46	-236.12	928.24	1:1.35:5.29
	2#横梁	-570.05	-359.64	1331.66	1:0.63:2.34
	3#横梁	-358.46	-306.19	493.08	1:0.85:1.38
	4#横梁	-125.77	-115.63	-986.34	1:0.92:7.84
5号索	1#横梁	356.99	-219.57	-350.47	1:0.62:0.98
	2#横梁	-193.33	-112.67	1083.06	1:0.58:5.6
	3#横梁	-79.07	-68.71	549.58	1:0.87:6.95
	4#横梁	155.24	80.77	-319.74	1:0.52:2.06
9号索	1#横梁	374.3	175.9	-333.92	1:0.47:0.89
	2#横梁	121.53	115.28	266.09	1:0.95:2.19
	3#横梁	215.57	214.22	-603.4	1:0.99:2.8
	4#横梁	-214.74	-180.212	349.78	1:0.84:1.63

	加密区段	外腹板	内腹板	中腹板	大致比例
1号索	1#横梁	320.66	422.6	433.9	1:1.32:1.35
	2#横梁	379.7	443.2	333.5	1:1.17:0.88
	3#横梁	447.7	473.2	342.2	1:1.06:0.76
	4#横梁	313.78	472.1	500.2	1:1.5:1.6
5号索	1#横梁	202.55	230.8	216.6	1:1.14:1.07
	2#横梁	243.23	262.4	168.7	1:1.08:0.69
	3#横梁	304.36	316.1	179.91	1:1.04:0.59
	4#横梁	193.02	281.90	243.90	1:1.46:1.26
9号索	1#横梁	113.49	115.11	152.74	1:1.01:1.35
	2#横梁	140.79	160.1	123.83	1:1.14:0.88
	3#横梁	183.54	204.29	152.67	1:1.11:0.83
	4#横梁	145.68	152.08	117.47	1:1.04:0.81

	加密区段	外腹板	内腹板	中腹板	大致比例
1号索	1#横梁	-189.92	-157.25	-82.53	1:0.83:0.43
	2#横梁	-148.99	-128.29	-122.59	1:0.86:0.82
	3#横梁	-134.48	-116.85	-114.69	1:0.87:0.85
	4#横梁	-261.23	-213.27	-196.85	1:0.82:0.75
5号索	1#横梁	-281.39	-229.54	-161.22	1:0.82:0.57
	2#横梁	-230.08	-195.72	-174.78	1:0.85:0.76
	3#横梁	-210.25	-176.54	-174.74	1:0.84:0.83
	4#横梁	-358.33	-306.84	-206.68	1:0.86:0.58
9号索	1#横梁	-421.5	-433.1	-346.3	1:1.02:0.82
	2#横梁	-417.7	-451.3	-316.9	1:1.08:0.76
	3#横梁	-395.8	-448.6	-315.8	1:1.13:0.8
	4#横梁	-530.5	-518.2	-374.4	1:0.98:0.71

	加密区段	外腹板	内腹板	中腹板	大致比例
1号索	1#横梁	267.41	225.01	199.99	1:0.84:0.75
	2#横梁	171.44	129.32	129.06	1:0.75:0.75
	3#横梁	178.9	138.14	132.89	1:0.77:0.74
	4#横梁	200.45	162.31	97.63	1:0.81:0.49
5号索	1#横梁	301.04	284.26	201.06	1:0.94:0.67
	2#横梁	173.31	170.86	162.09	1:0.99:0.94
	3#横梁	184.12	183.35	157.12	1:1.0:0.85
	4#横梁	222.09	214.31	144.15	1:0.96:0.65
9号索	1#横梁	360.75	369.4	278.1	1:1.02:0.77
	2#横梁	257.56	277	192.79	1:1.08:0.75
	3#横梁	299.69	293.5	191.92	1:0.98:0.64
	4#横梁	276.31	275	294.2	1:1.0:1.06