吉林大学学报(工学版) ›› 2020, Vol. 50 ›› Issue (1): 66-76.doi: 10.13229/j.cnki.jdxbgxb20180835
刚性折纸机构运动分析及折叠过程仿真
- 哈尔滨工业大学 机电工程学院,哈尔滨 150001
Kinematic analysis and simulation of folding process for rigid origami mechanisms
Zhen GUO( ),Hong-ying YU(
),Hong-ying YU( ),Zhong-xin HUA,Di ZHAO
),Zhong-xin HUA,Di ZHAO
- School of Mechatronics Engineering, Harbin Institute of Technology, Harbin 150001, China
摘要:
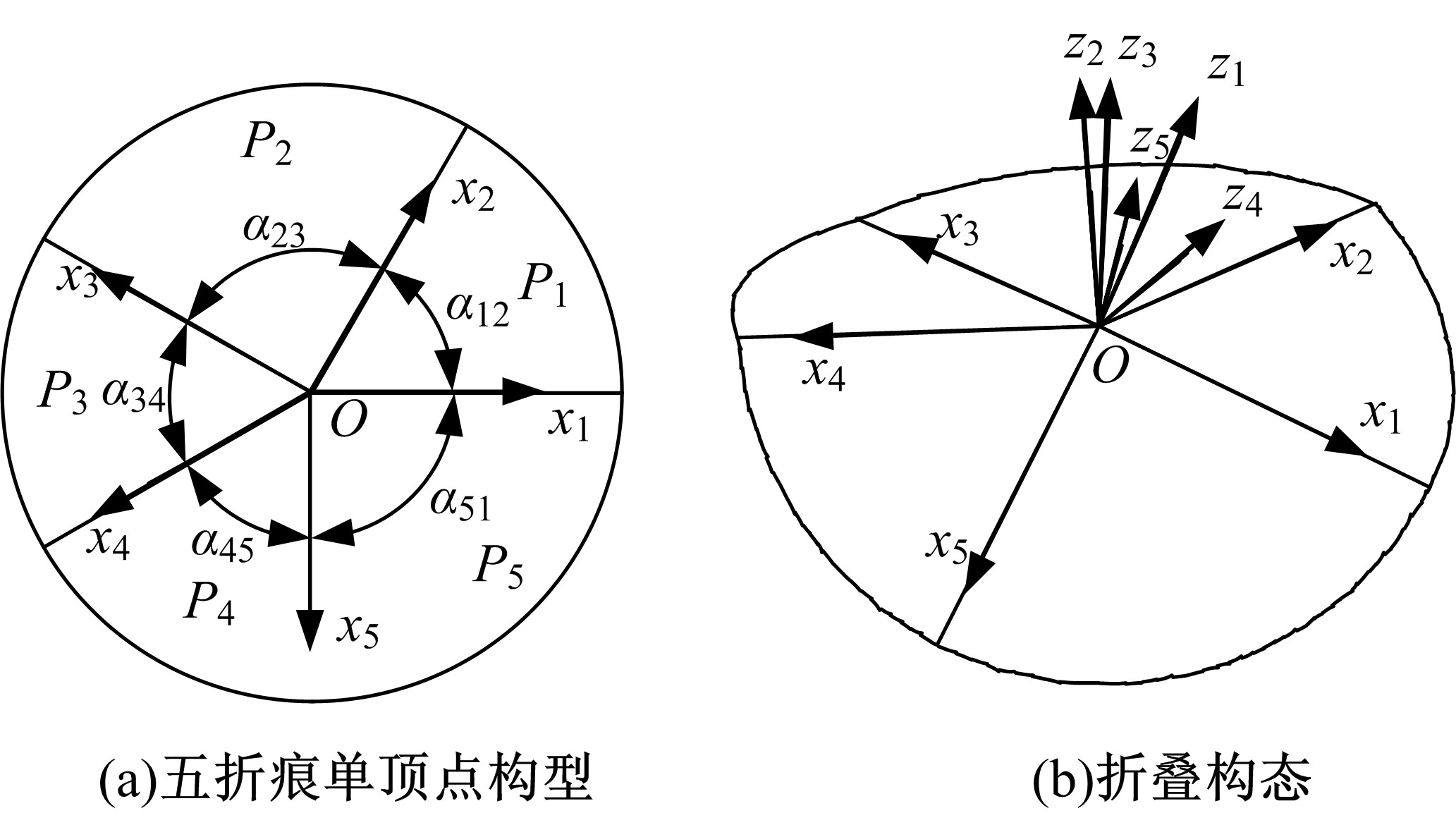
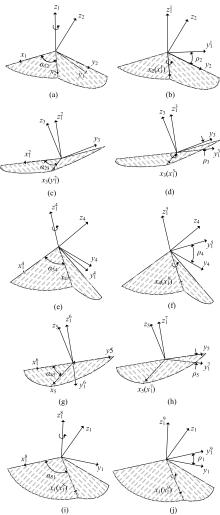
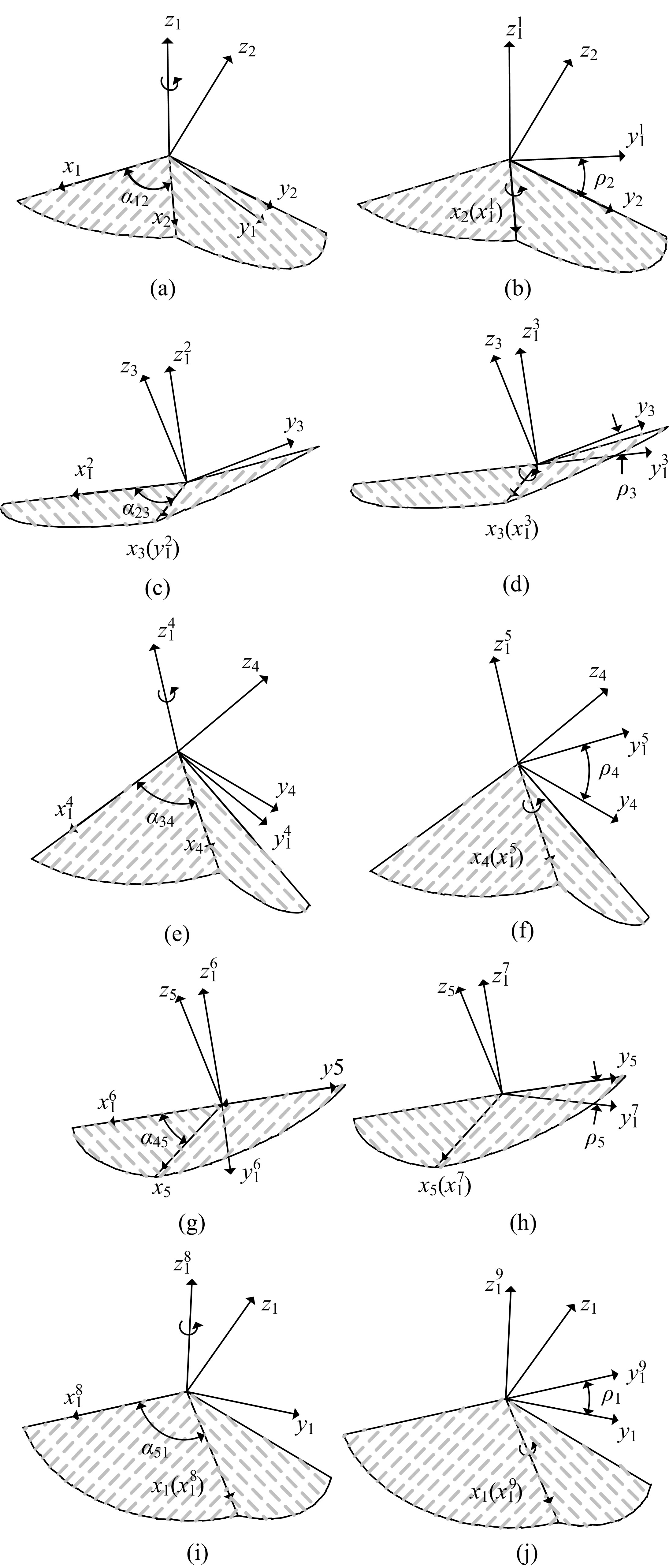
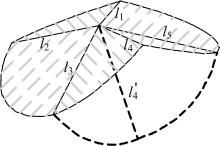
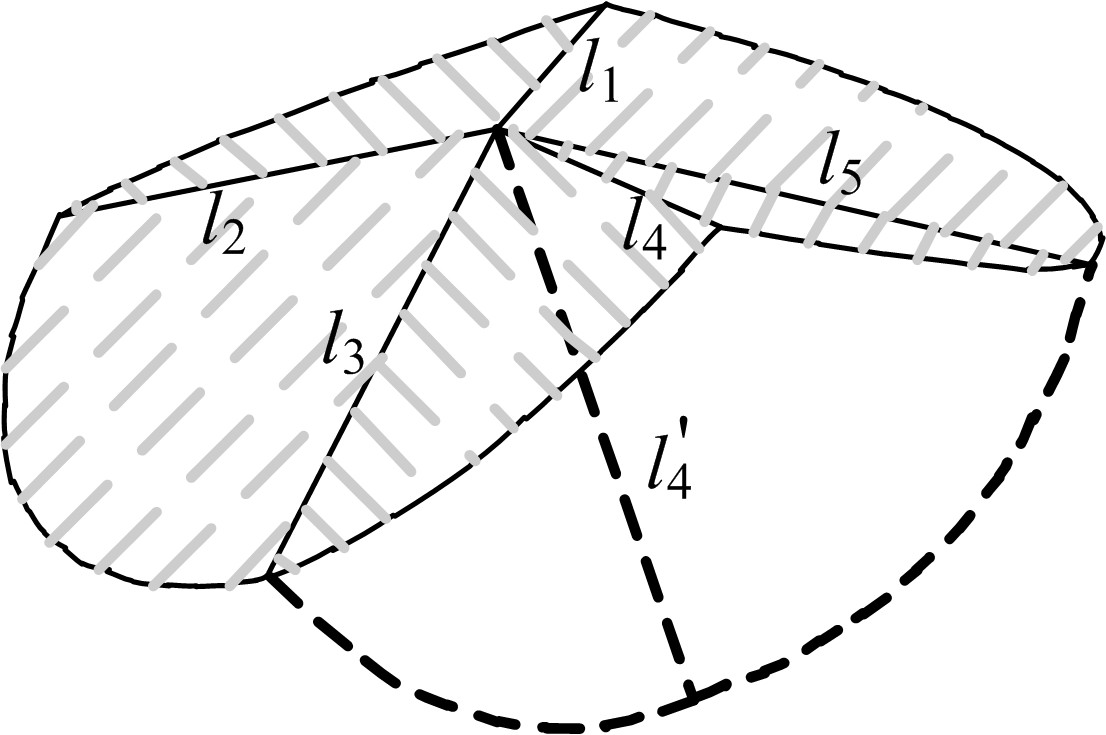
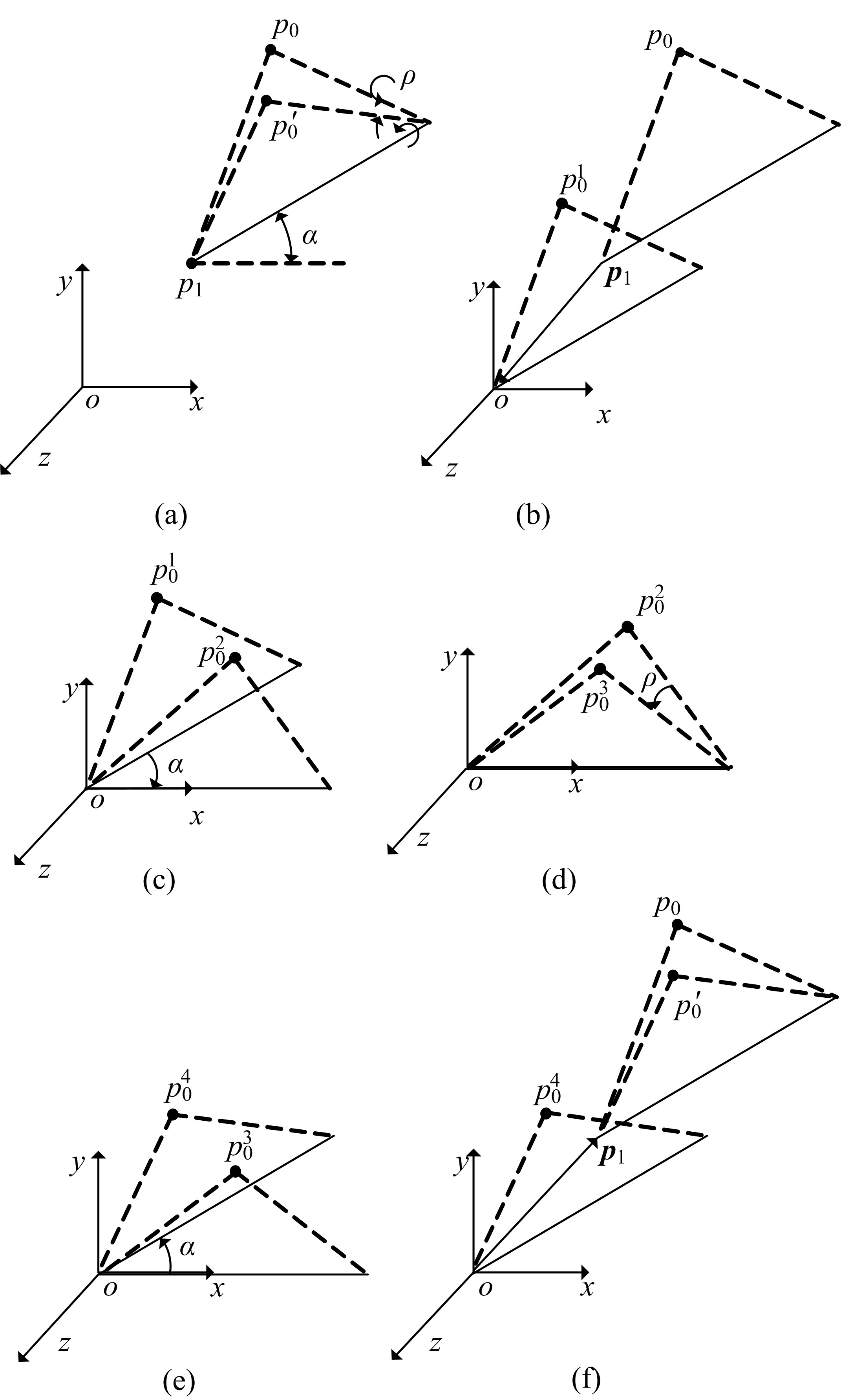
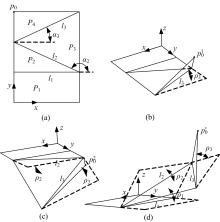
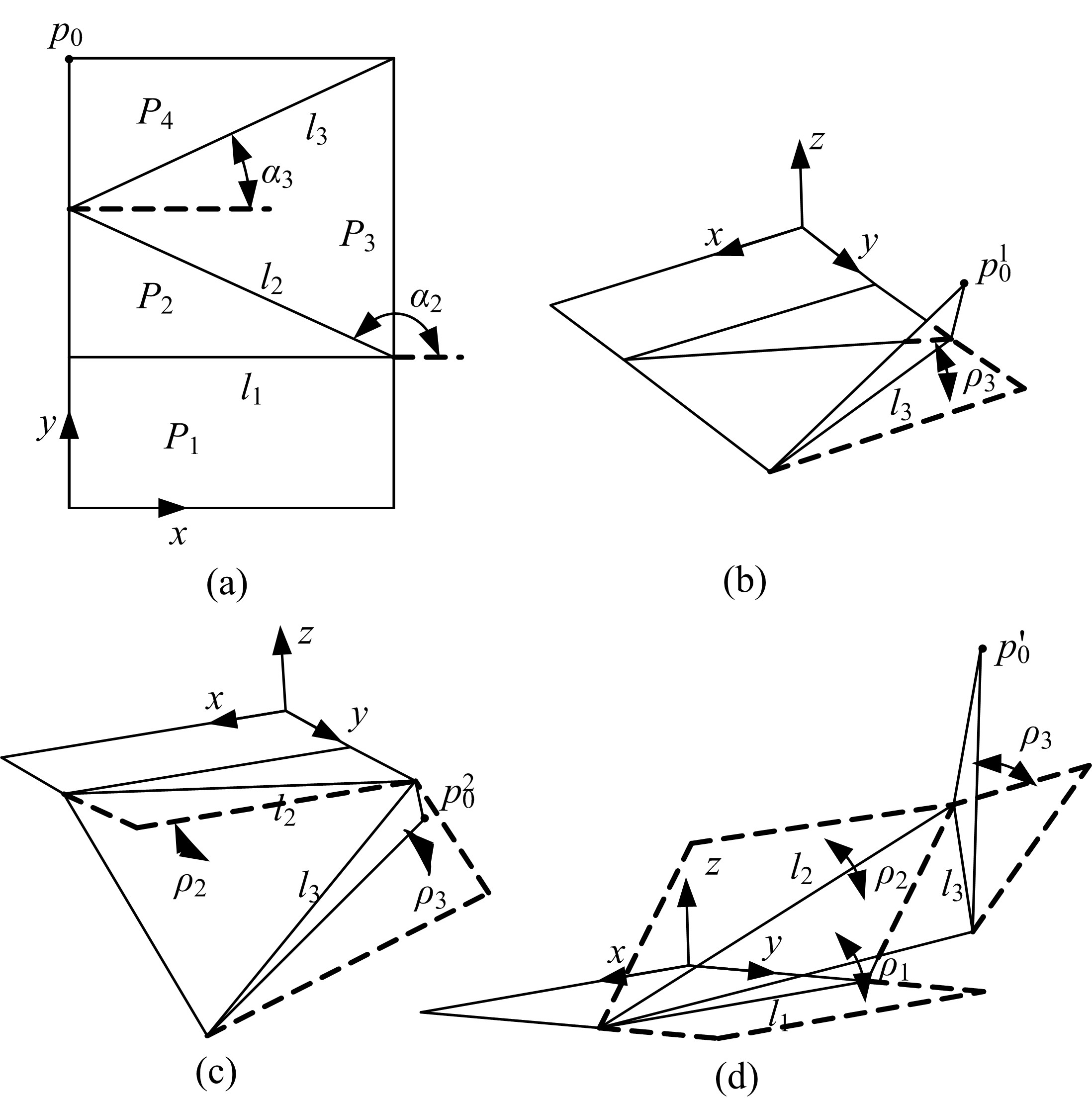
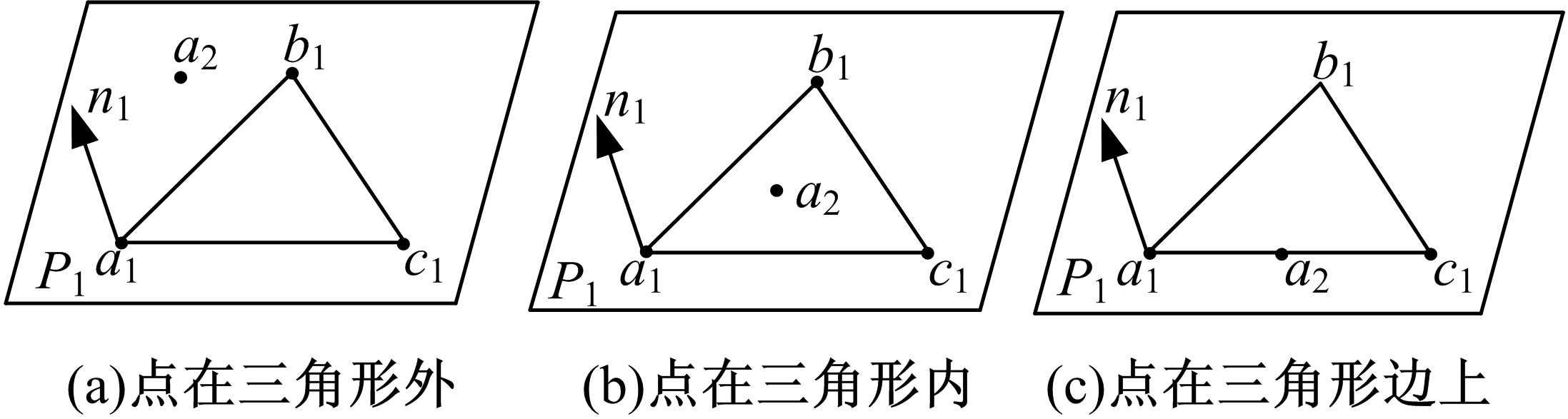
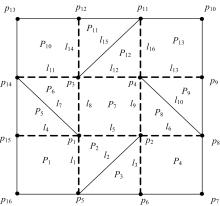
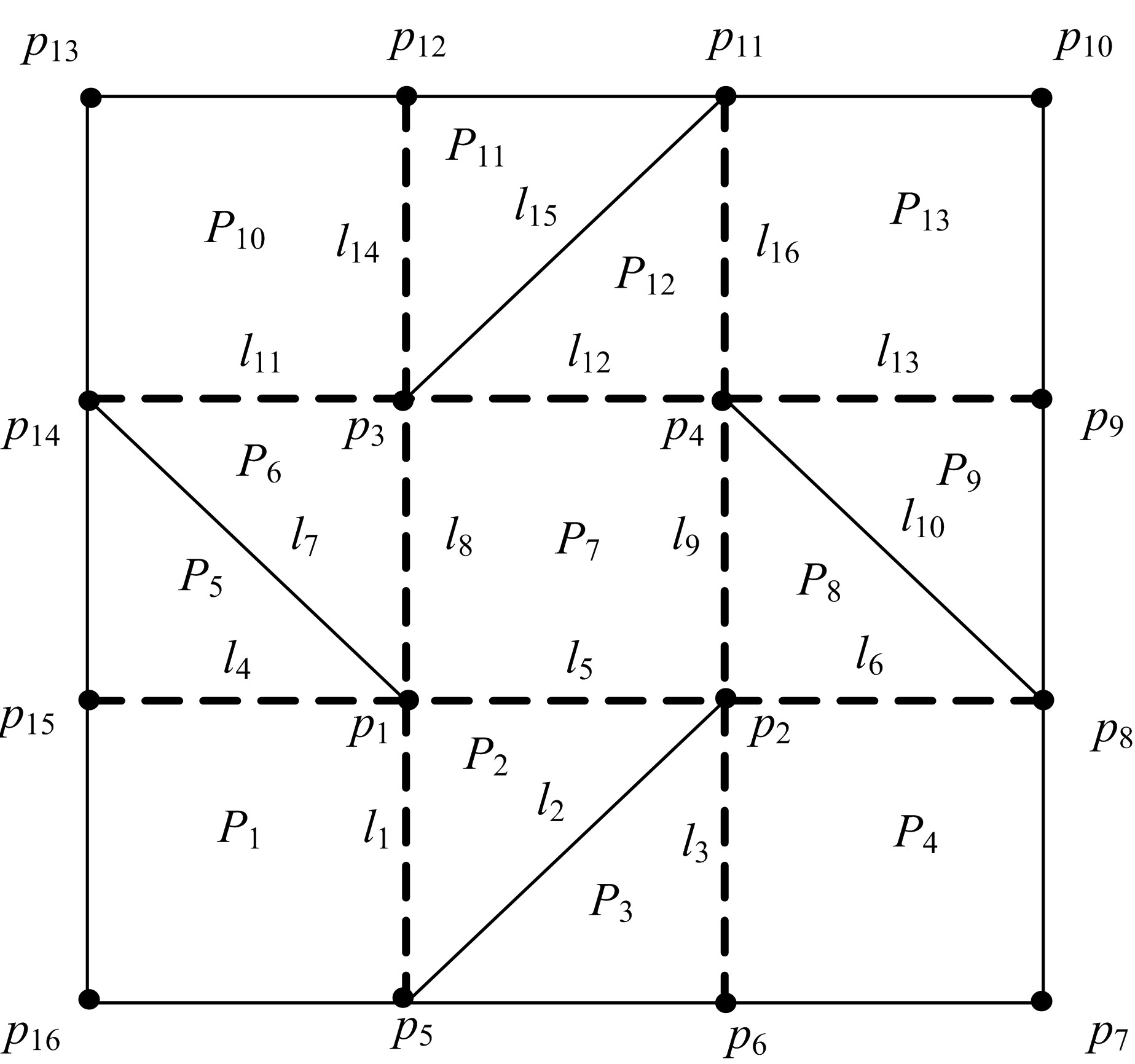
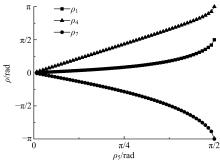
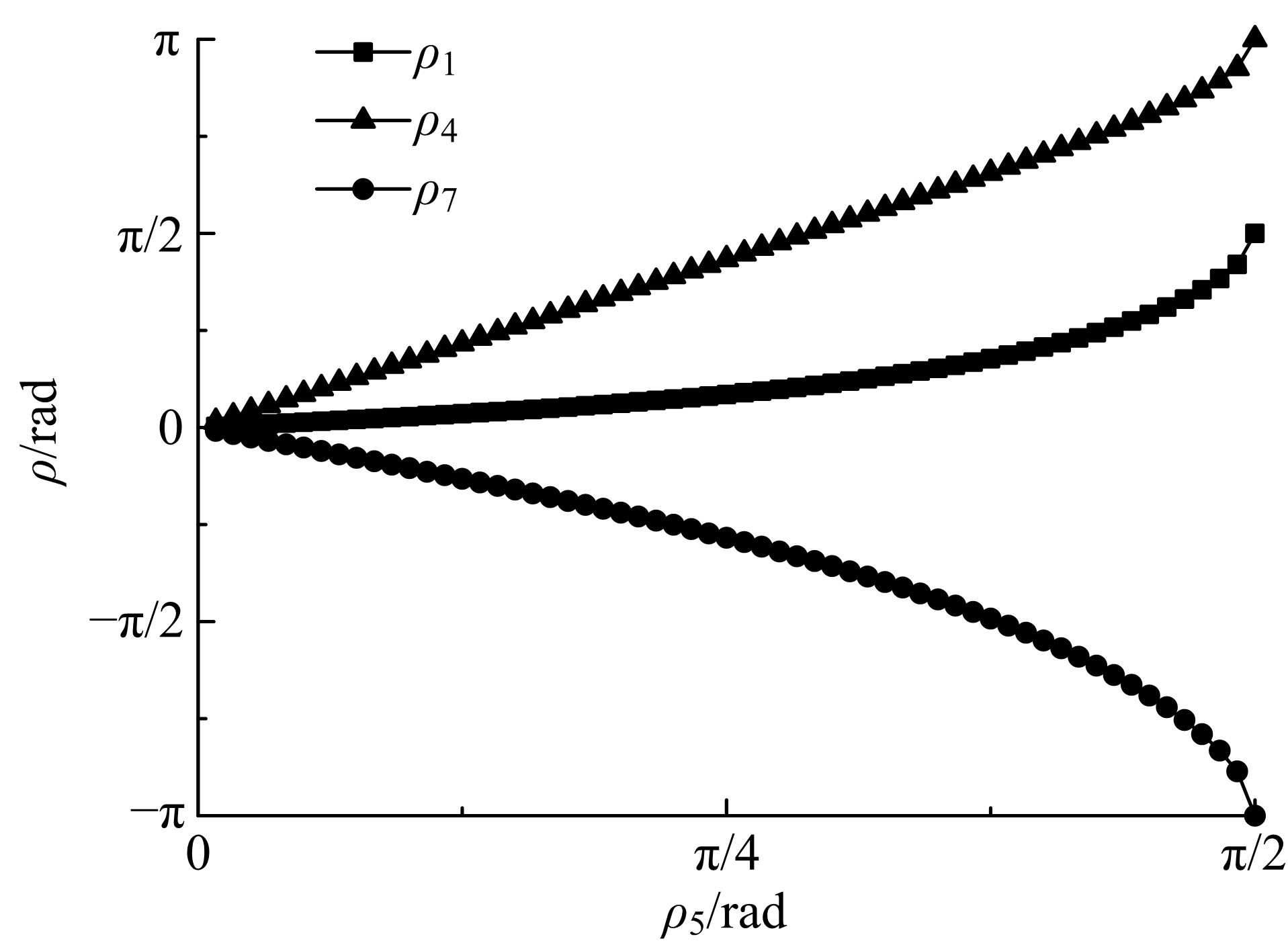
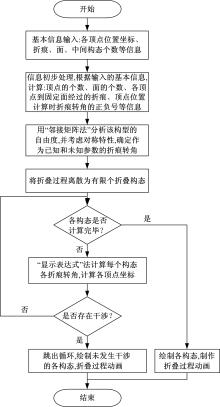
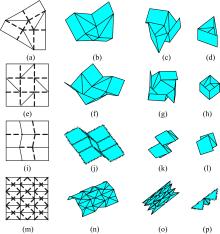
为了分析刚性折纸机构的运动特性,研究了不同构型的折叠过程,建立了刚性折纸机构运动学模型并分析了典型构型的折叠构态。首先,建立单顶点刚性折纸机构各折痕转角之间的关系方程,推导出未知折痕转角的显式表达式,并通过方程解的互验排除干扰解,得到任意折叠构态实际折痕转角;其次,通过旋转变换矩阵,计算任意折叠构态下顶点实时位置坐标;再次,将三角面片对相交判断算法应用到刚性折纸机构干涉判断上,检测折叠过程中的干涉情况;最后,建立折叠过程仿真平台,并分析典型刚性折纸机构的折叠过程。仿真分析结果与实际折叠过程一致,验证了刚性折纸机构运动分析方法的正确性以及仿真平台的适用性。
中图分类号:
- TH112
| 1 | Chen Y, Rui P, Zhong You. Origami of thick panels[J]. Science, 2015, 349(6246): 396-400. |
| 2 | Chen Y, Fan L Z, Feng J. Kinematic of symmetric deployable scissor-hinge structures with integral mechanism mode[J]. Computers and Structures, 2017, 191: 140-152. |
| 3 | Wei G W, Chen Y, Jian S. Dai. Synthesis, mobility, and multifurcation of deployable polyhedral mechanisms with radially reciprocating motion[J]. Journal of Mechanical Design-Transactions of the ASME, 2014, 136(9): 91003-91015. |
| 4 | Tachi T. Rigid origami mechanisms[J]. Journal of the Robotics Society of Japan, 2016, 34(3): 184-191. |
| 5 | Zachary A, Jason C, Erik D D, et al. Rigid origami vertices: conditions and forcing sets[J]. Journal of Coumputational Geometry, 2016, 7(1): 229-237. |
| 6 | Balkcom D J, Mason M T. Robotic origami folding[J]. International Journal of Robotics Research, 2008, 27(5): 613-627. |
| 7 | Tomohiro Tachi. Simulation of rigid origami[C]∥Origami 4: Proceedings the 4th International Meeting of Origami Mathematics, Science, and Education. Natick, Massachusetts: A K Peters, 2009. |
| 8 | An B, Benbernou N, Demaine E D, et al. Planning to fold multiple objects from a single self-folding sheet[J]. Robotica, 2011, 29(1): 87-102. |
| 9 | Wu W N, Zhong Y. A solution for folding rigid tall shopping bags[J]. Proceedings Mathematical Physical and Engineering Sciences, 2011, 467(2133): 2561-2574. |
| 10 | Chen Y, Feng J. Improved symmetry method for the mobility of regular structures using graph products[J]. Journal of Structural Engineering, 2016, 142(9): 51-65. |
| 11 | Chen Y, Feng J, Liu Y Q. A group-theoretic approach to the mobility and kinematic of symmetric over-constrained structures[J]. Mechanism and Machine Theory, 2016, 105: 91-107. |
| 12 | Chen Y, Feng J. Folding of a Type of deployable origami structures[J]. International Journal of Structural Stability and Dynamics, 2012, 12(6): 193-202. |
| 13 | Xi Z H, Lien J M. Plan folding Motion for rigid origami via discrete domain sampling[C]∥IEEE International Conference on Robotics and Automation, Seattle, Washington, 2015: 2938-2943. |
| 14 | Liu S C, Lv W L, Chen Y, et al. Deployable prismatic structures with rigid origami patterns[J]. Journal of Mechanisms and Robotics, 2015, 8(3): No.031002. |
| 15 | Cai J G, Zhang Y T, Xu Y X, et al. The Foldability of cylindrical foldable structures based on rigid origami[J]. Journal of Mechanical Design, 2016, 138(3): No.031401. |
| 16 | Peraza H E A, Hartl D J, Akleman E, et al. Modeling and analysis of origami structures with smooth folds[J]. Computer-Aided Design, 2016, 78: 93-106. |
| 17 | Yu H Y, Guo Z, Wang J R. A method of calculating the degree of freedom of foldable plate rigid origami with adjacency matrix[J]. Advances in Mechanical Engineering, 2018, 10(6): 969-989. |
| 18 | Tomas Möller. Fast triangle-triangle intersection test[M]. Wellesley:A K Peters, 1997. |
| 19 | Tropp O, Tal A, Shimshoni I. A fast triangle to triangle intersection test for collision detection[J]. Computer Animation and Virtual Worlds, 2006, 17(5): 527-535. |
| 20 | 于海燕,何援军. 空间两三角形的相交问题[J]. 图学学报, 2013, 34(4): 54-62. |
| Yu Hai-yan, He Yuan-jun. Testing the intersection status of two triangles[J]. Journal of Graphics, 2013, 34(4): 54-62. | |
| 21 | 关立文,戴玉喜,王立平. 空间三角面片对相交判断算法[J]. 清华大学学报:自然科学版, 2017,57(9): 970-974. |
| Guan Li-wen, Dai Yu-xi, Wang Li-ping. Intersection test algorithm for spacial triangular facets[J]. Journal of Tsinghua University (Science and Technology), 2017, 57(9): 970-974. |
| [1] | 朱伟,王传伟,顾开荣,沈惠平,许可,汪源. 一种新型张拉整体并联机构刚度及动力学分析[J]. 吉林大学学报(工学版), 2018, 48(6): 1777-1786. |
| [2] | 毛宇泽, 王黎钦. 鼠笼支撑一体化结构对薄壁球轴承承载性能的影响[J]. 吉林大学学报(工学版), 2018, 48(5): 1508-1514. |
|
||